Quantum private comparison of arbitrary single qubit states based on swap test

Xi Huang(黄曦) Yan Chang(昌燕) Wen Cheng(程稳) Min Hou(侯敏) and Shi-Bin Zhang(张仕斌)

1School of Cybersecurity,Chengdu University of Information Technology,Chengdu 610225,China

2Sichuan Key Laboratory of Advanced Cryptography and System Security,Chengdu 610225,China

Keywords: quantum private comparison,arbitrary single qubit states,swap test,quantum cryptography

1. Introduction

The quantum information science has made considerable progress,especially in the quantum cryptography field,so far.Quantum cryptography based on the principle of quantum mechanics rather than the computational complexity of solving mathematical problems has a considerable advantage of security over classical cryptography. Since the first quantum cryptographic protocol was proposed by Bennett and Brassard[1]and its unconditional security was proved in 1984, numerous quantum cryptographic protocols have been proposed to solve various cryptographic tasks,such as quantum key distribution(QKD),[1-4]quantum key agreement(QKA),[5-7]quantum secret sharing (QSS),[8-11]quantum secure direct communication(QSDC),[12-14]and quantum private query(QPQ).[15-18]

Secure multiparty computation (SMC) aims to calculate a function in a distributed network of mutual distrust without disclosing the raw content of each party’s private inputs. As an important branch of SMC,the first private comparison was proposed by Yao[19]in the millionaires’ problem to compare two millionaires who are richer without revealing their actual property. According to Yao’s millionaires’ problem, Boudotet al.[20]suggested a private comparison protocol to compare the equality of two millionaires’ actual property. However,the existing private comparison protocols that are based on the computational complexity of solving mathematical problems have security vulnerabilities due to the strong capability of quantum computing. To solve this problem, some researchers began to combine the classical private comparison and quantum mechanics to perform the private comparison.In 2009, Yang and Wen[21]proposed the first QPC protocol,which encodes Hash values into EPR pairs to compare two participants’private inputs. Since then, many QPC protocols based on various quantum states have been proposed, for example,the QPC protocols based on single particle,[22-26]Bell states,[21,27-31]multi-particle entangle states,[32-37]and cluster state.[38-42]Since Lo[43]pointed out that it is impossible to evaluate the equality function in a two-party scenario securely,a semi-honest third party(TP)was introduced in QPC protocols to guarantee security.Except for comparing whether two parties’private inputs are equal,some scholars set out to compare the size relationship of secret integers,which means that multi-participants can compare the size of their secret inputs. Linet al.[44]successfully proposed a QPC protocol of size relation with d-level Bell states. Guoet al.[45]presented a QPC protocol of size relation based on entanglement swapping of d-level Bell states. Yuet al.[46]put forward a QPC protocol of size relation by using d-level single-particle states. Ye and Ye[47]proposed two multiparty quantum private comparison(MQPC)protocols of size relation with two semi-honest TPs and one semi-honest TP by using d-level single-particle states. Songet al.[48]proposed an MQPC by using singleparticle states.

Furthermore,the swap test,[49]as a simple and basic algorithm in quantum computing, which was used to put forward a quantum cryptographic protocol, is a research focus. The goal of swap test is to evaluate the similarity of the two qubits.By measuring the probability that the ancilla qubit is in state|1〉or|0〉,the square of the inner product of two qubits is obtained. Based on the idea of swap test,quantum signature,[50]quantum neural networks,[51-53]have been proposed.

To the best of our knowledge,all existing QPC protocols are mainly based on entangled states, and the proposed QPC protocol based on swap test has not yet appeared. Moreover,the previous QPC protocols mainly focus on the comparison of secret integers. This paper proposes a QPC protocol of arbitrary single qubit states by using swap test for the first time.Two participants’ qubits can be compared by executing this protocol. In this protocol,two participants encrypt their qubits by using rotation operation and sent it to TP. By performing the swap test,the TP can obtain the comparison result of two participants’ encrypted qubits. If the measurement result is 0, it indicates that two participants’ private inputs are equal.Otherwise,it is not identical. Security analysis shows that our protocol possesses good performance in resisting both outside attacks and participants’ attacks. Compared with the existing QPC protocols, the proposed one can compare the equality of two participants’qubits and secret integers. Besides, it does not require any entanglement swapping technology, and qubits are compared by performing swap test,which is easier to implement with current technology. Finally, the proposed protocol is extended to QPC of arbitrary single qubit states by using multi-qubit swap test.

The rest of this paper is organized as follows. Swap test is introduced in Section 2. The detailed description of the proposed QPC of arbitrary single qubit states based on swap test is given in Section 3. Multi-qubit swap test and the proposed QPC of arbitrary single qubit states by using multi-qubit swap test are described in Section 4. Finally,some conclusions are drawn in Section 5.

2. Swap test

Swap test was firstly introduced in Ref. [49]. It aims to evaluate the similarity between arbitrary two qubits. By measuring the probability that the ancilla qubit is in state|1〉or|0〉,we can obtain the square of the inner product of two qubits.The quantum circuit of swap test is shown in Fig.1.

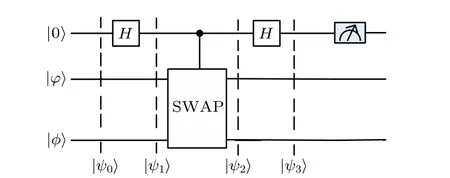
Fig.1. Quantum circuit of the swap test.

Supposing that there are two qubits|φ〉and|φ〉,as well as an ancilla qubit|0〉,which constitute an initial quantum state

Thus, we can obtain the square of the inner product of two qubits|φ〉and|φ〉,i.e.,|〈φ|φ〉|2=1-2P(|1〉).

If two qubits|φ〉and|φ〉are the same, equation (4) becomes|0〉(|φ,φ〉+〈φ,φ|). The measurement result of the ancilla qubit is|0〉. However, if two qubits|φ〉and|φ〉are not the same, the measurement result of the ancilla qubit will be either|0〉with a probability of (1/2)+(1/2)|〈φ|φ〉|2or|1〉with a probability of (1/2)-(1/2)|〈φ|φ〉|2. Therefore, two qubits|φ〉and|φ〉are different if the measurement result of the ancilla qubit is|1〉. We cannot make sure that two qubits|φ〉and|φ〉are the same if the measurement result of the ancilla qubit is|0〉. Further,the error probability of the swap test fornqubits can be given by

The error probability of the swap test can be reduced to anyδ ＞0 by performing the swap testλtimes,resulting in an error probability belowδ,whereλ ∈O(log21/δ).

Theorem 1 Let|φ〉=cosα0|0〉+sinα0|1〉and|φ〉=cosα1|0〉+sinα1|1〉be arbitrary qubits,by performing swap test on them,the probability of the ancilla qubit in state|1〉is(1/2)-(1/2)cos2(α0-α1).

Proof By performing swap test on|φ〉= cosα0|0〉+sinα0|1〉and|φ〉=cosα1|0〉+sinα1|1〉, the probability of the ancilla qubit in state|1〉can be given by

be the rotation operation, which is used to encrypt|φ〉and|φ〉. By performing swap test on the encrypted|φ〉and|φ〉,the probability of the ancilla qubit in state|1〉is (1/2)-(1/2)cos2(α0-α1).

Proof Using the rotation operation

According to Theorem 1 and Theorem 2, it can be concluded that the same rotation operationR(θ) applied to|φ〉and|φ〉does not change the probability for the ancilla qubit to reside in state|1〉by performing swap test.

3. Proposed QPC of arbitrary single qubit states based on swap test

3.1. QPC protocol description

Suppose that there are two participants, says Alice and Bob,who want to compare whether their secret qubits|φi〉=cosαi|0〉+sinαi|1〉and|φi〉=cosβi|0〉+sinβi|1〉are equal under the semi-honest third party TP), whereαi,βi∈[0,π].The TP may behave improperly, but she is not allowed to conspire with any participant. Assume that the protocol runs in ideal conditions (i.e., there are no technical errors and the transmission channels are lossless and noiseless),then the proposed QPC of arbitrary single qubit states based on swap test will be able to be described as follows.

Step 5 By performing Steps 1-4λtimes,if in the measurement results of the ancilla qubit there exists|1〉, TP announces Alice’s (Bob’s) qubits are different. If the measurement results of the ancilla qubit are all|0〉,the TP announces that Alice’s(Bob’s)qubits are equal.

3.2. Security analysis

In this subsection,the security of the proposed QPC protocol is analyzed from the prospect of both outsider attacks and participants’attacks.

3.2.1. Outsider attacks

Since the confidentiality of Alice (Bob’s) qubits are encrypted with rotation operation and the decoy photons technology is adopted to guarantee the security of qubit transmission,besides,the corresponding rotation operations are unknown to Eve, she cannot learn anything about Alice’s (Bob’s) qubits.Thus,Eve has to adopt some common attack strategies to steal something about Alice’s (Bob’s) qubits as much as possible,such as the intercept-resend attack,the direct measurement attack, the entangle-measure attack, the man-in-the-middle attack,and the Trojan horse attacks.

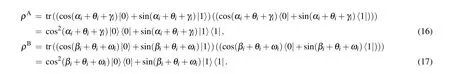
However, the measurement outcomeMAi(MBi) is encrypted with the secret keyθiandγi(ωiandγi), she cannot infer the confidentiality of Alice(Bob’s)qubits without knowingθi(ωiorγi).

Case 3 Entangle-measure attack

The entangle-measure attack is that Eve intercepts the transmitted qubits and performs the unitary operationUto entangle the prepared ancilla qubits in state|E〉and the intercepted qubits. The unitary operationUis given by

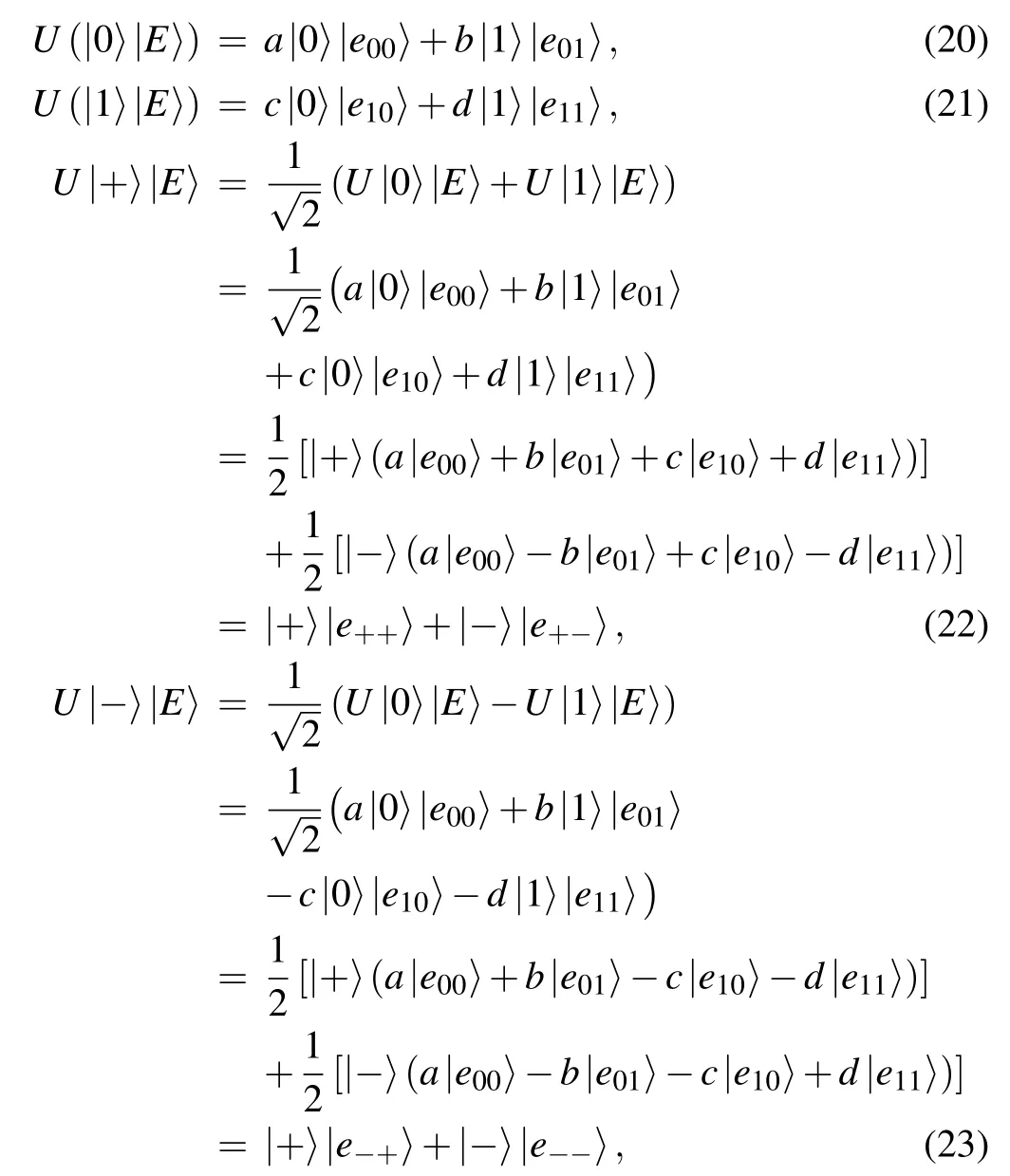
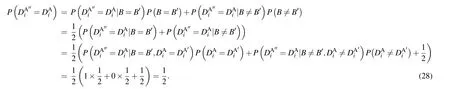
The man-in-the-middle attack can be detected in the security check process with a probability of 1-(1/2)δ, whereδis the number of decoy photons. The probability that Eve is detected is approximate to 1 whenδis sufficiently large.Therefore, the man-in-the-middle attack is invalid. Similarly,the same method can show that Eve cannot derive Bob’s qubits by performing the man-in-the-middle attack either.

Case 5 Trojan horse attacks

The Trojan horse attacks mainly include the invisible photon eavesdropping attack and the delay-photon attack.[54]To prevent it, wavelength quantum filters and photon number splitters must be equipped.[16,17]However, the proposed QPC protocol is a one-way communication protocol,the Trojan horse attacks does not work,and it can be prevented automatically.

According to the above analysis, it can be deduced that the proposed protocol possesses good performance in resist outsider attacks.

3.2.2. Participants’ attacks

Participants’ attacks are more powerful than outsider attacks and the participants have more opportunities and advantages to attack the QPC protocol because they know partial information and can legally utilize this information. Two cases are considered as follows.

Case 1 Security against malicious Alice(Bob)

3.3. Comparison

The comparison mainly focuses on the following aspects:quantum state used,quantum measurement,need of entanglement swapping,quantum communication,the technology used and content of comparison. The comparison results between the presented QPC protocol and several representative QPC protocols are shown in Table 1.

Table 1. Comparison results between proposed QPC protocol and several representative QPC protocols.

Compared with other representative QPC protocols, the propose QPC protocol has many advantages as follows. (i)It provides a new method to compare two participants’qubits and it can compare the equality of two participants’qubits and secret integers.(ii)It does not require any entanglement swapping technology, and it only needs rotation operations and swap test, which is easier to implement with current technology. (iii)It is a one-way communication protocol,and it cannot equip wavelength quantum filters or photon number splitters to resist the Trojan horse attack.

4. Expansibility

4.1. Multi-qubit swap test

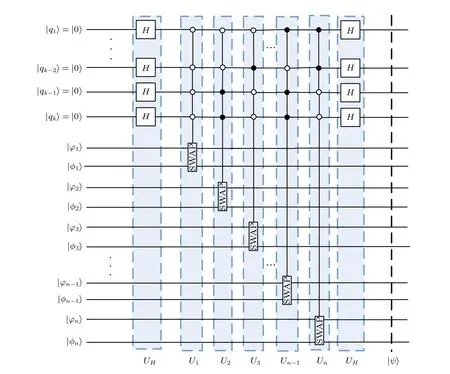
Fig.2. Quantum circuit of the multi-qubit swap test.

In Fig.2,the unitary operators corresponding to the quantum circuit of the multi-qubit swap test in each box are shown as follows:

According to Eq.(31),the probability that|qk-1〉and|qk〉stay in state|1〉is given by

Therefore,nqubit pairs (|φi〉,|φi〉) are different if the measurement result of the ancilla qubit is|1〉.We cannot make sure that n qubit pairs(|φi〉,|φi〉)are the same if the measurement result of the ancilla qubit is|0〉. Further,the error probability can be given by

The error probability of the swap test can be reduced to anyδ ＞0 by performing the swap testγtimes,resulting in an error probability belowδ,whereγ ∈O(log21/δ).

Theorem 3 Let|φi〉=cosαi|0〉+sinαi|1〉and|φi〉=cosβi|0〉+sinβi|1〉be arbitrary qubits,and perform the multiqubit swap test on them, the probability that the ancilla qubit|qk-1〉and|qk〉are in state|1〉will be

Proof By performing swap test on|φi〉= cosαi|0〉+sinαi|1〉and|φi〉=cosβi|0〉+sinβi|1〉, the probability that the ancilla qubit|qk-1〉and|qk〉are in state|1〉can be given by

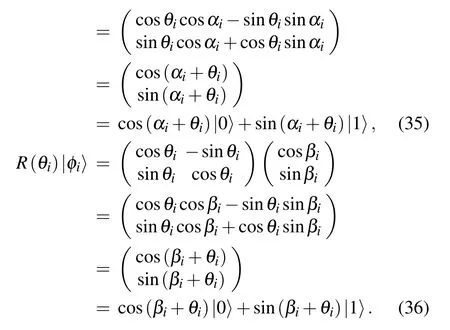
By performing the multi-qubit swap test on the encrypted|φi〉and|φi〉, the probability that the ancilla qubit|qk-1〉and|qk〉reside in state|1〉can be written as

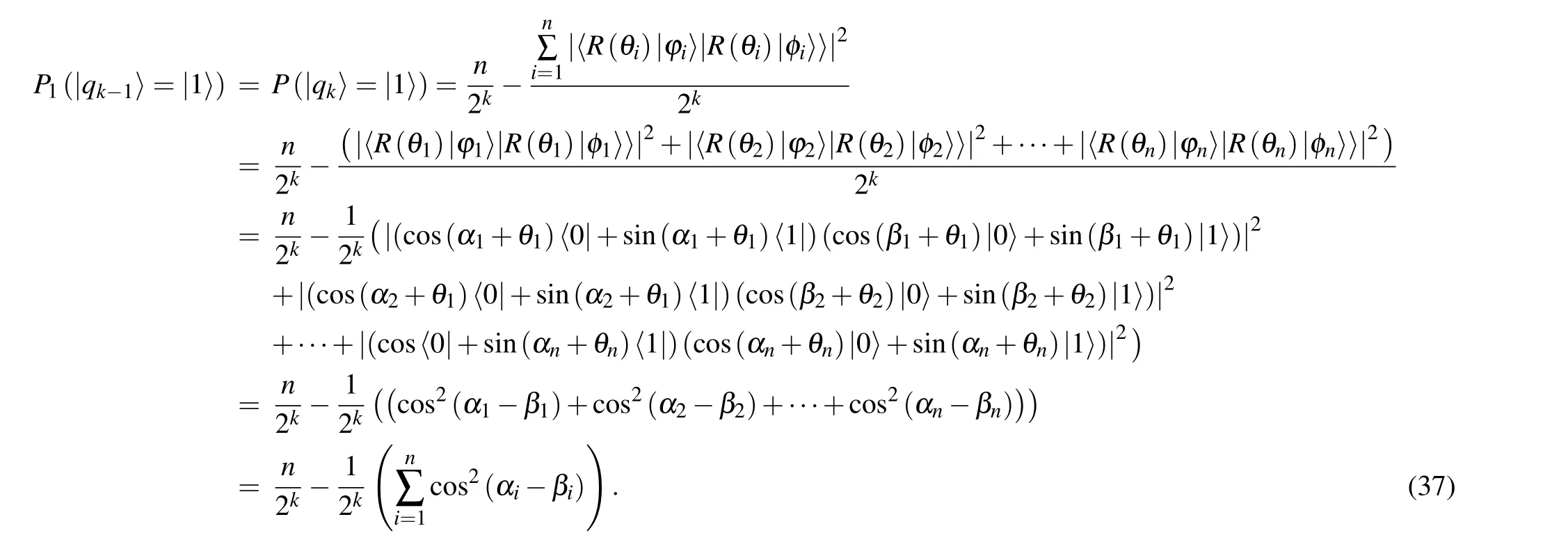
According to Theorems 3 and 4,it can be concluded that the same rotation operationR(θi)applied to|φi〉and|φi〉does not change the probability that the ancilla qubit|qk-1〉and|qk〉stay in state|1〉by performing the multi-qubit swap test.

4.2. QPC protocol of arbitrary single qubit states by using multi-qubit swap test

The proposed QPC protocol of arbitrary single qubit states based on the swap test needs to performirounds of comparison in the worse condition. To reduce comparison times and perform one comparison, the proposed QPC protocol is extended to the QPC of arbitrary single qubit states by using the multi-qubit swap test. The only difference between these two protocols lies in Step 4. Here, the QPC protocol of arbitrary single qubit states based on the multi-qubit swap test is described. Steps 1-3 are the same as those in the proposed QPC protocol of arbitrary single qubit states based on the swap test.

Step 5* By performing Steps 1-4γtimes,if the measurement results of the ancilla qubit|qk-1〉and|qk〉both possess|1〉, it is indicated that Alice’s(Bob’s)qubits are different. If the measurement results of the ancilla qubit|qk-1〉and|qk〉are both|0〉,it is implied that Alice’s(Bob’s)qubits are equal. Finally,TP announces the comparison results to Alice and Bob.

Now we come to discuss the security of the proposed QPC protocol of arbitrary single qubit states based on the multi-qubit swap test. In these two protocols, rotation operations and the decoy particle technology are used to guarantee the security of qubits transmission,and Steps 1-3 in these two protocols are identical. Hence,their security analysis is identical. Security analysis in Subsection 3.2 shows that the proposed QPC of arbitrary single qubit states based on the swap test can resist both the outsider attacks and the participants’attacks. Therefore,the proposed QPC of arbitrary single qubit states based on the multi-qubit swap test can resist both the outsider attacks and the participants’attacks as well.

5. Conclusions

To sum up,in this paper,by using the swap test,the first quantum private comparison of arbitrary single qubit states is proposed. The participants can compare their secrets by performing the proposed QPC protocol without revealing their private information. In this protocol, Alice and Bob use rotation operations and decoy particle technology to guarantee the security of qubits transmission. Their qubits are encrypted by performing rotation operations and are sent to TP.After the TP performs the swap test on the encrypted qubits,the TP can know whether their secrets are equal and she announces the comparison results to the participants. Additionally, the proposed protocol can compare secret integers as well. It encodes secret integers into the amplitude of quantum state,and the encoded quantum state is compared by performing this protocol.In the process of comparison,TP cannot learn anything about Alice’s(Bob’s)qubits except the comparison results. The security analysis demonstrates that the proposed QPC protocol is secure against both the outsider attacks and the participants’attacks. Finally, to reduce comparison times, the proposed QPC protocol is extended to the QPC of arbitrary single qubit states by using the multi-qubit swap test.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 62076042), the Key Research and Development Project of Sichuan Province, China (Grant Nos.2020YFG0307 and 2021YFSY0012), the Key Research and Development Project of Chengdu Municipality, China(Grant No. 2019-YF05-02028-GX), the Innovation Team of Quantum Security Communication of Sichuan Province,China (Grant No. 17TD0009), and the Academic and Technical Leaders Training Funding Support Projects of Sichuan Province,China(Grant No.2016120080102643).