Studies on aluminum powder combustion in detonation environment

Jian-Xin Nie(聂建新), Run-Zhe Kan(阚润哲), Qing-Jie Jiao(焦清介), Qiu-Shi Wang(王秋实),Xue-Yong Guo(郭学永), and Shi Yan(闫石)

State Key Laboratory of Explosion Science and Technology,Beijing Institute of Technology,Beijing 100081,China

Keywords: aluminum particle combustion model,aluminum powder,burn rate equation,burning time

1. Introduction

As a high-energy metal fuel, aluminum has been widely used in high-energy explosives[1,2]to increase explosive energy and damage power.[3,4]Compared with ideal explosives,aluminized explosives are typical nonideal explosives,and the detonation process is more complicated. In recent years,studies on the explosive reaction mechanism of aluminized explosives have been extensive,[5,6]but there are few studies on the combustion of aluminum powder in detonation environments. In addition,research on aluminum powder combustion has been mostly carried out under normal pressure and normal temperature environmental conditions. It remains a challenge to study the aluminum powder combustion model in the detonation environment with ultrahigh temperature, ultrahigh pressure and strong convection characteristics formed by detonation explosions. The study of the combustion theory of aluminum particle in detonation environment is of great significance to further understand the explosion mechanism of aluminized explosives,improve the energy release rate of aluminized explosives and enrich the theoretical model of combustion of metal powder.

Burning time in any combustion environment is an important parameter for aluminum combustion research. Researchers have studied the aluminum burning time and the influence of various parameters on the burning time.Glassman[7]proposed that the combustion of metal particles obeys theD2law,that is,the burning time of particles is proportional to the square of the particle size, which is consistent with the pure droplet combustion model. Friedman and Maˇcek[8]proposed that for combustion without fragmentation,the burning time is proportional to the 1.5 power of the particle diameter. However,if the gas and vapor diffuse to the surface of the particles(or oxides)in the model and the reaction is a surface type, then the burning time may be proportional toD. The relationshiptc～D1.2-1.5was established through experiments. In the same year,Davis[9]reported the relationship oftc～D1.8. Brzustowski and Glassman[10]first established a single spherical aluminum particle static combustion model based on the diffusion rate of reactants in an oxygencontaining gas closed chamber. Their model considered that the reaction of aluminum particle is mainly the gas-phase reaction between aluminum vapor and oxidizing gas. After deduction,the burn rate of aluminum particle is inversely proportional to the square of the diameter,so the model is also called the classicD2model.Belyaevet al.[11]modified theD2model based on a large amount of experimental data,and further corrected the square of the particle size in theD2model proposed by Glassman to the 1.5 power. In 1973,Law[12,13]established a diffusion-controlled combustion model for aluminum particles based on theD2model and conservation equations of mass and energy. Studies have shown that oxides diffusing into particles will increase the burn rate of aluminum particles,while oxides diffused into the surrounding environment have little effect on the burn rate. Brooks and Beckstead[14]proposed amendments to theD2law by analyzing a large amount of experimental data. The burning time of aluminum particles was proportional toD1.5-1.8.Tanguayet al.[15]performed aluminum particle combustion experiments using a detonation tube. Their results showed that aluminum particles tend to burn in a kinetically limited manner when they are accelerated in highly convective flows, conforming to theD0.5.Houim[16]developed a calculation model for the interaction between shock waves and a reacting aluminum droplet. The results showed that the combustion of aluminum droplets may be kinetically controlled mechanisms. The shock waves reduce the evaporation rate for nonreacting aluminum droplets,while increasing the burning rate when chemical reactions are considered.

In recent years, researchers have used experimentation and simulation to study the combustion of aluminum powder under different conditions. Sundaram[17]tried to determine the key physical and chemical processes of particle combustion by summarizing the latest progress in the study of nano aluminum particle combustion and determining the combustion mechanism under different particle sizes and pressures by comparing the time scales in various studies. Glorian[18]solved the effect of heterogeneous reactions in the process of aluminum combustion through a numerical simulation of single aluminum combustion particles and considered both the gas phase and surface dynamics mechanisms. Lombaet al.[19]conducted a constant volume combustion experiment of micron aluminum-magnesium powder, and the results showed that the flame temperature of aluminum powder with an average particle size of less than 12 µm was close to the particle surface temperature. Analysis of the combustion products further confirmed the existence of a gas phase reaction.Sundaram[20]proposed the general theory of ignition and combustion of nano and microaluminum particles, which is the best theory to date. He divided the oxidation process into four stages according to the phase transition and chemical reaction.In the first stage,the particles are heated to the melting temperature of the aluminum core. The second stage starts when the aluminum core melts. In the third stage, nanoparticles react violently with oxidation gas. In the fourth stage, large particles are combusted by the gas phase or surface reactions.Yunchaoet al.[21]studied the ignition and combustion of a single aluminum particle size (40 µm-160 µm) in a hot gas flow. The total ignition and combustion process of aluminum particles can be divided into three stages: preheating,ignition and combustion. The burning timetccan be well described byD1.0. Vladimir[22]studied the effect of molecular oxygen on the combustion of aluminum nanoparticles in water vapor.The model analysis showed that a small amount of oxygen (mole fractions 1%-3%)can accelerate the combustion of aluminum in steam by an approximate order of magnitude. This study is of great significance for research into aluminum and different reactive gases. In 2021,Braconnieret al.[23]considered a new experimental setup to image and study the combustion of a single burning aluminum droplet(30µm-130µm),and proposed a new Beckstead-style empirical correlation for burning times. The burning time is proportional to the 1.72 power of the particle size.

In summary, scholars from various countries have performed much research on the combustion model of aluminum particles under normal pressure and high-temperature(＜1000 K) environments. However, the determination of the burning time is mostly based on experimental data fitting,which lacks theoretical derivation. For detonation environments, such as combustion environments with high temperature, high pressure, and high-speed movement characteristics, theoretical studies have been insufficient. In this study,an aluminum particle combustion model is established within a detonation environment,and the burn rate equation for a single aluminum particle is derived. Furthermore, by considering the particle size distribution,the burn rate equation of aluminum powder is given and verified by electrical conductivity measurements. This may theoretically explain the combustion process of aluminum particle after detonation wave.

2. Detonation environment combustion model

There is a layer of alumina shell on the surface of aluminum particles, forming a typical “core-shell” structure.Jiaoet al.[24]studied the core-shell response process of aluminum particles subjected to detonation shock waves. After detonation,the aluminum particles were squeezed by the detonation wave,the shell on the windward side was cracked and broken,and then the particles rebounded and stretched. Under the action of peeling of the surrounding high-speed detonation products and internal aluminum core stress,the shell was massively crushed and peeled, and the internal aluminum vapor contacted and combusted with the detonation products. Due to the velocity difference between the detonation products and particles, alumina could not adhere to the surface of the aluminum,so the aluminum continued to vaporize and combust.

The combustion model of aluminum particles is shown in Fig.1. To simplify the model, the following points are assumed:

(i)Under the action of detonation waves,the shell of the aluminum particles breaks and is peeled off immediately.

(ii) The aluminum particle vaporization process is static and isotropic.

(iii)Aluminum particles started burning in the form of a gas-phase reaction.

(iv) The decreases in system temperature decreases caused by heat conduction and heat radiation are not considered.

(v)The local hot spots generated by the surface combustion of aluminum particles are ignored, as it is believed that the combustion temperature of aluminum particles is uniform.

Fig.1. Combustion model of a single particle aluminum powder in a detonation environment.

Based on the above analysis and assumptions, the combustion of aluminum particles in a detonation environment can be divided into the following three stages.

The first stage Under the action of the detonation wave,the alumina shell is peeled off, and the high-temperature environment generated by the detonation makes the aluminum particles heat up. Aluminum particles deform under the impact of detonation wave, and cracks appear on the windward side and begin to fracture. Under the action of peeling of the surrounding high-speed detonation products and internal aluminum core stress, the shell crushes and is peeled on a large scale. At the same time,the aluminum particles heat up in the high-temperature environment created by the detonation.

The second stage The aluminum particles are vaporized at high temperature, and the aluminum atoms react with the detonation products. When the alumina shell is peeled off,the detonation products contact the aluminum core, and aluminum particles vaporize, diffuse, and combust. Moreover,the combustion temperature of aluminum particles is higher than the vaporization point of aluminum, the aluminum particles continue to vaporize, and the aluminum vapor further reacts with the detonation products. Due to the velocity difference between the detonation products and the aluminum core,the surface of the aluminum particles formed a separate tail flame.

The third stage Due to the relative movement of the solid and gas,the aluminum combustion products undergo“purge”diffusion until the aluminum particles are completely vaporized and the combustion ends. The combustion products of aluminum move in the direction of the detonation products with their velocity faster than that of the core, so the combustion products do not adhere to the surface of the core. The aluminum particles continue to vaporize until the combustion is complete.

3. Combustion control equation

According to the model assumptions,aluminum particles are combusted in a gaseous state, so the dimensionless burn rate of the aluminum particles ˙Wccan be expressed as the product of the dimensionless vaporization rate ˙Wvof the particles,the diffusion coefficientΩof the product and the probability of the oxidation reactionRr:

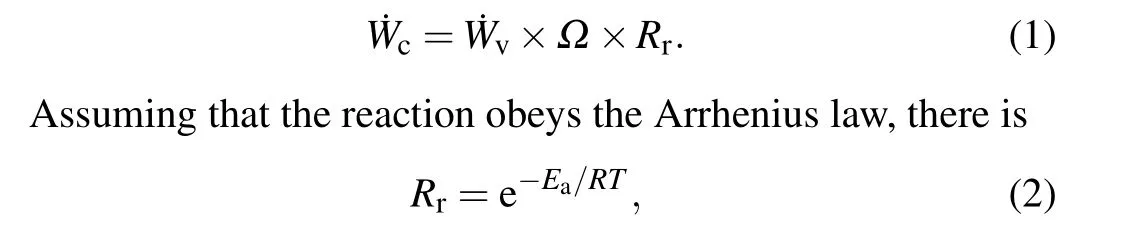
whereTis the system temperature,Eais the activation energy of the gaseous aluminum atom oxidation reaction,andRis the universal gas constant with a value of 8.314 J/(mol·K).

Therefore, to obtain the dimensionless burn rate of aluminum particles, it is necessary to analyse the dimensionless vaporization rate ˙Wvof the particles and the diffusion coefficientΩof the product.

3.1. Vaporization equation

According to the combustion model,the aluminum particles have a combustion reaction with the detonation products in the form of a gas-phase reaction,so the vaporization of aluminum is the prerequisite for the combustion reaction of aluminum particles.

Aluminum atoms are strongly attracted by other atoms in a condensed phase(including liquid aluminum and solid aluminum). Usually,aluminum atoms do not leave the surface of condensed matter due to this attraction. However,when solid aluminum is heated, some aluminum atoms obtain more energy than their vaporization enthalpyEv, and they “escape”the surface of the condensed aluminum and vaporize. According to Boltzmann’s law,

whereNis the number of atoms escaping the surface,Cis the total number of atoms in any region,andEvis the enthalpy of vaporization of aluminum.

Assuming that the surface area occupied by each atom on the surface of the condensed aluminum isA, the average velocity isv, and it has enough energy to move a distance of 2r(the diameter of the first layer atom). Then, the time that the aluminum atom passes through this distance is the time to leave the aluminum surface of the condensed phase. This time can be expressed as 2r/v, so the number of aluminum atoms evaporated per unit time can be

whereNvis the number of atoms vaporized per unit area per unit time,Ais the cross-sectional area of each atom in unit m2,vis the average rate of atoms in units m/s,ris the radius of the atom,andris the radius of an aluminum atom in unit m.

According to the kinetic theory of molecules, the average molecular velocity has the following relationship with the temperature of the system:

where ˙mvis the mass rate of aluminum vaporization per unit area,in units kg/(m2·s).

It can be seen from Eq. (7) that the vaporization rate of condensed aluminum per unit area per unit time is mainly determined by the system temperature. The higher the system temperature is,the greater the vaporization rate of aluminum.

Assuming that the aluminum particles are spherical, for spherical aluminum particles,aluminum atoms evaporate from the surface, as shown in Fig. 2. Therefore, the vaporization rate of the spherical condensed phase per unit time can be expressed as

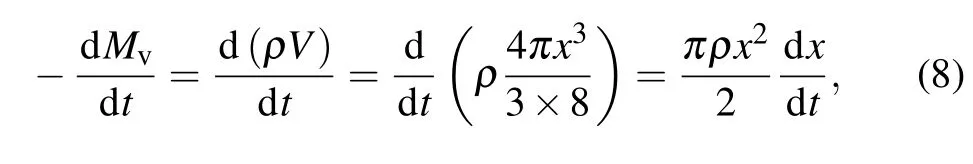
where dMv/dtis the mass vaporization rate of aluminum particles, dx/dtis the radial scale vaporization rate of aluminum particles,Vis the volume of spherical aluminum particles,xis the diameter of spherical aluminum particles, andρis the density of aluminum.

Fig.2. Diagram of the atomic vaporization process on the surface of spherical aluminum particles.

whereWvis the dimensionless evaporation fraction of aluminum particles.

By differentiating Eq. (14) to obtain the dimensionless vaporization rate ˙Wv,

To calculate the diffusion coefficient of aluminum particles,the finite element software AUTODYN is employed. The model is composed of TNT,aluminum,and alumina,as shown in Fig.3. TNT explosives are described by the JWL equation of state, and the left of the surface is detonated. The constitutive equation of aluminum is described by the Von Mises model, and the constitutive equation of alumina is described by the JH model.Meanwhile,points 1-4 are set to monitor the movement speed of detonation products and aluminum nuclei.

As shown in Fig.4,the initial breaking point appears on the surface of the aluminum shell under the action of detonation wave, and then the aluminum shell is broken, so that the contact combustion of aluminum and detonation products.The higher the intensity of the detonation wave is,the stronger the fragmentation degree of the alumina shell and the greater the diffusion coefficient. The diffusion coefficients of different explosives obtained by calculation are given in Table 1.Due to the speed difference between the detonation product and the aluminum particle, after the aluminum particle shell is broken, the speed difference accelerates the peeling of the alumina shell,which promotes the contact and combustion of the aluminum particle and the detonation product.

Therefore, it can be seen from the equation that the dimensionless evaporation rate of aluminum particles is inversely proportional to the particle diameter and increases with increasing ambient temperature.

3.2. Diffusion coefficient

According to the model in Section 2, the surface of the aluminum shell is broken by the detonation wave,and the oxidation reaction starts from the broken place. Therefore, the degree of aluminum particle crushing determines the rate of the combustion reaction. This study introduces the dimensionless diffusion coefficientΩ, which is defined as the ratio of the purge area of the detonation wave to the surface area of the spherical aluminum particles. The ratio depends on the relative movement speed of the detonation product and the aluminum particles and is related to whether the product condenses on the aluminum surface and the actual diffusion area of the aluminum.

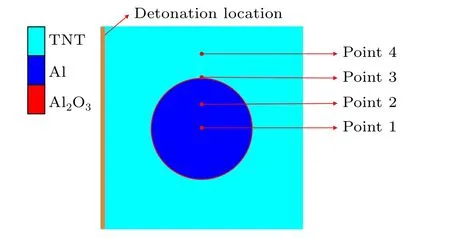
Fig.3. Simulation calculation simplified model.

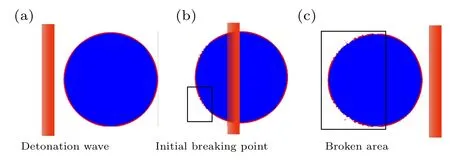
Fig.4. The crushing process of aluminum core and alumina shell.

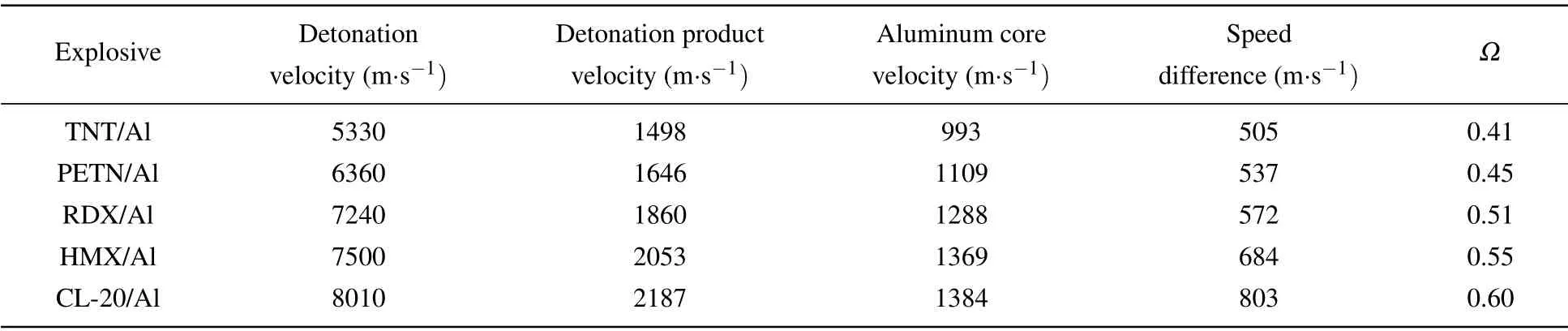
Table 1. Diffusion coefficient with different detonation wave intensities.

3.3. Combustion equation of aluminum particles

With the purge diffusion model, adding the product dimensionless diffusion coefficientΩ,equation(1)can be transformed into the dimensionless burn rate of aluminum particles

Therefore,when the system temperature is higher than the vaporization temperature of aluminum,the burn rate and burn ratio are determined by the vaporization enthalpy. When the system temperature is low, the sublimation rate of aluminum particles is very low, so the activation energy of aluminum plays a major role.

WhenEais much less thanEv,equation(1)can be

It can be seen from Eq.(22)that the burning time of the aluminum particles are mainly affected by the particle size,system temperature,and diffusion coefficient.

Equations (20) and (21) are used to calculate the timedependent curves of the burn ratio and burn rate of 10-µm aluminum particles at different system temperatures,as shown in Fig.5.

From the curve change in Fig. 5, the initial burn rate of aluminum particles is the largest, and the burn rate decreases as the reaction time increases. As the system temperature decreases,the initial burn rate of the aluminum particles continues to decrease, and the burning time gradually increases.This is because temperature directly affects the burn rate equation and changes the vaporization enthalpy to indirectly affect combustion. The higher the temperature, the smaller the aluminum gasification enthalpy,the easier the vaporization combustion,and the higher the burn rate.

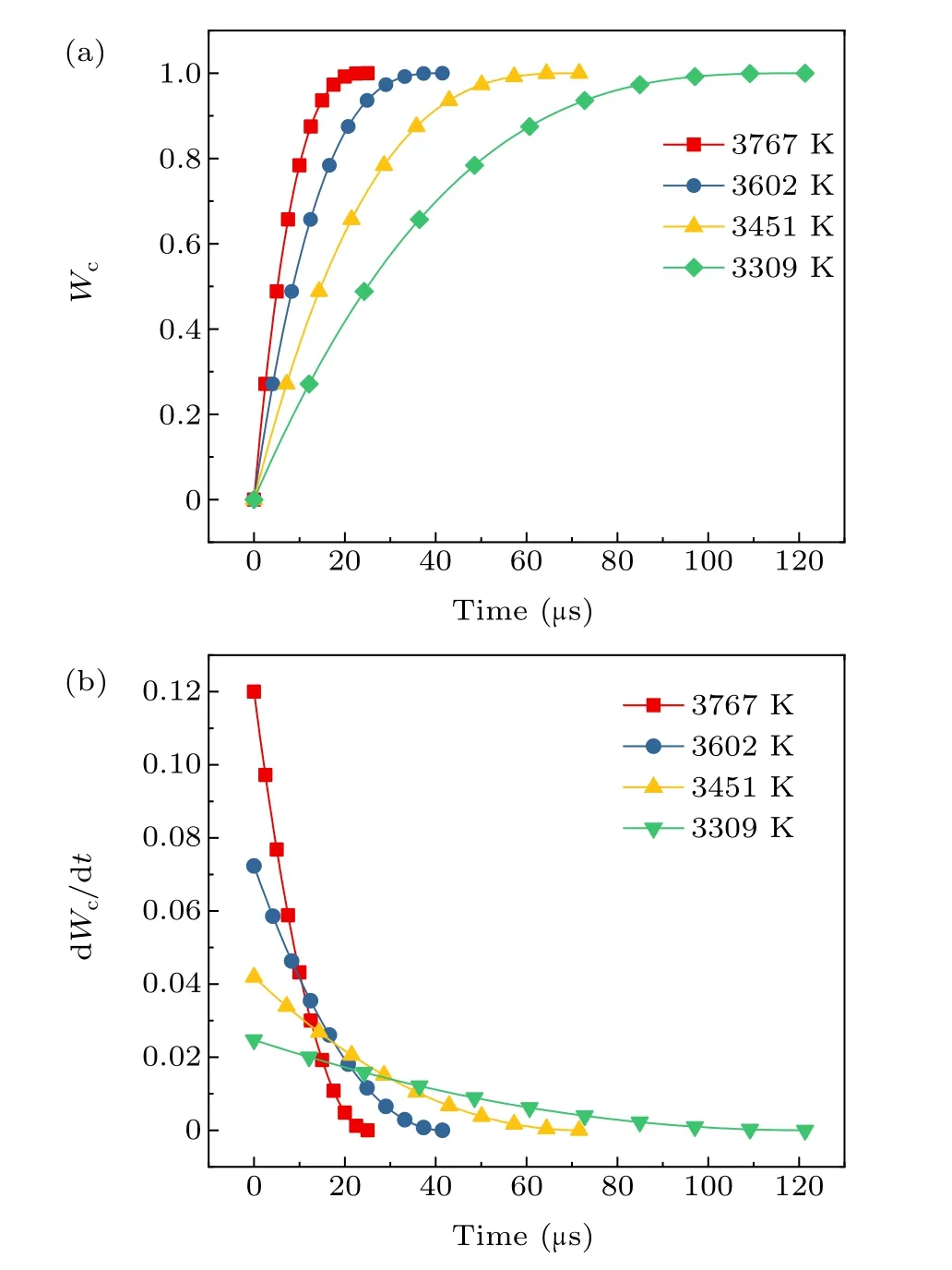
Fig. 5. (a) The burn ratio and (b) the burn rate of aluminum particles at system temperatures of 3309 K,3451 K,3602 K,and 3761 K.

Fig. 6. (a) The burn ratio and (b) burn rate of aluminum particles sizes of 2µm,10µm,50µm,and 100µm at a system temperature of 3602 K.

The changes in the burn ratio and burn rate of aluminum particles with different particle sizes for the same system temperature over time are shown in Fig.6.

Figure 6 shows that the reaction rate of aluminum particle is the largest at the beginning of the reaction. As the reaction time increases,the burn rate gradually decreases. As the particle size increases,the initial burn rate decreases continuously,and the burning time gradually increases. This is because the reaction rate is inversely proportional to the particle size. The larger the particle is,the lower the burn rate and the longer the burning time.

3.4. Combustion equation of aluminum powder

The particle size analysis results[25]show that the particle size of aluminum powder meets a lognormal distribution,expressed as follows:

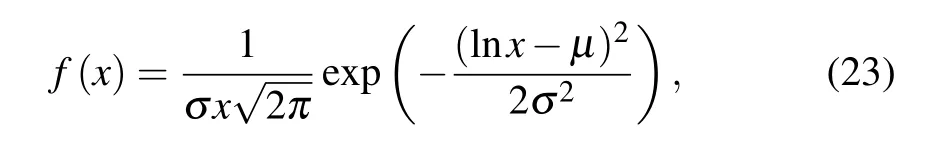
whereµandσare the parameters of the lognormal distribution fitting function.

According to statistical law, 99.9% of aluminum particle can be covered by the calculation of particle size [d50-3σ,d50+3σ]. The equation of the burn ratio and burn rate of aluminum powder can then be expressed as follows:

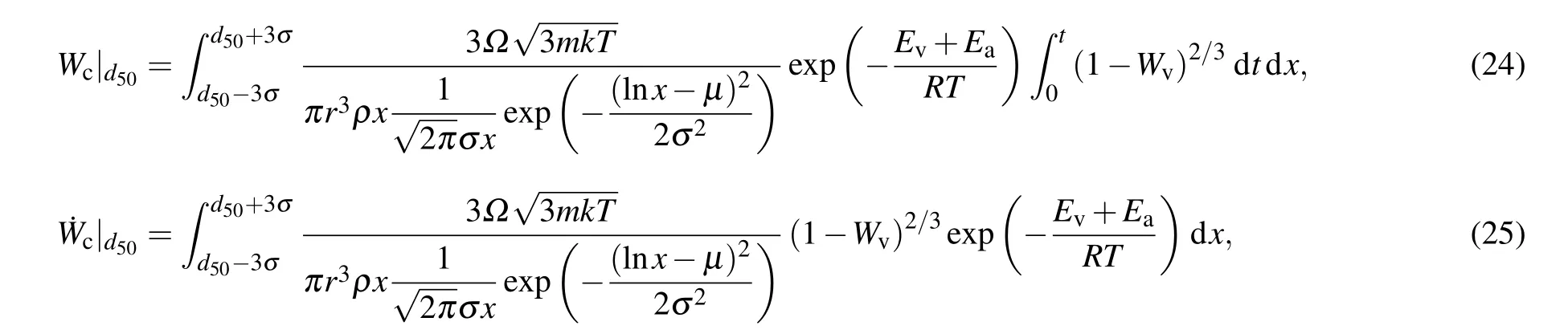
whered50is the median diameter in unitµm.According to the equation,there are two main parameters affecting the combustion degree and burn rate of aluminum powder: the combustion temperature,T,and the particle size distribution.

4. Electrical conductivity test

It is difficult to directly test the burn rate of aluminum powder in a detonation environment by using experimental methods, so conductivity testing[26,27]is used for indirect proof. This research group has improved the traditional coaxial test method, eliminated the bypass resistance effect, increased the effective time,and improved the sensitivity of the conductivity experiment. Figure 7 shows a schematic diagram of the improved conductivity experimental device.

Fig.7. Test arrangement of the experiment.

According to Hayes[28]of the Los Alamos Laboratory,it is known that the electrical conductivity of detonation products has a strong correlation with the solid carbon content in detonation products. Both the explosive detonation reaction and the oxidation-reduction reaction of Al and CO can reduce a large amount of conductive carbon. Therefore,the chemical reaction rate of the detonation reaction zone and the expansion zone of the detonation product can be determined through conductivity experiments to obtain the burning rate of the aluminum powder.[29]

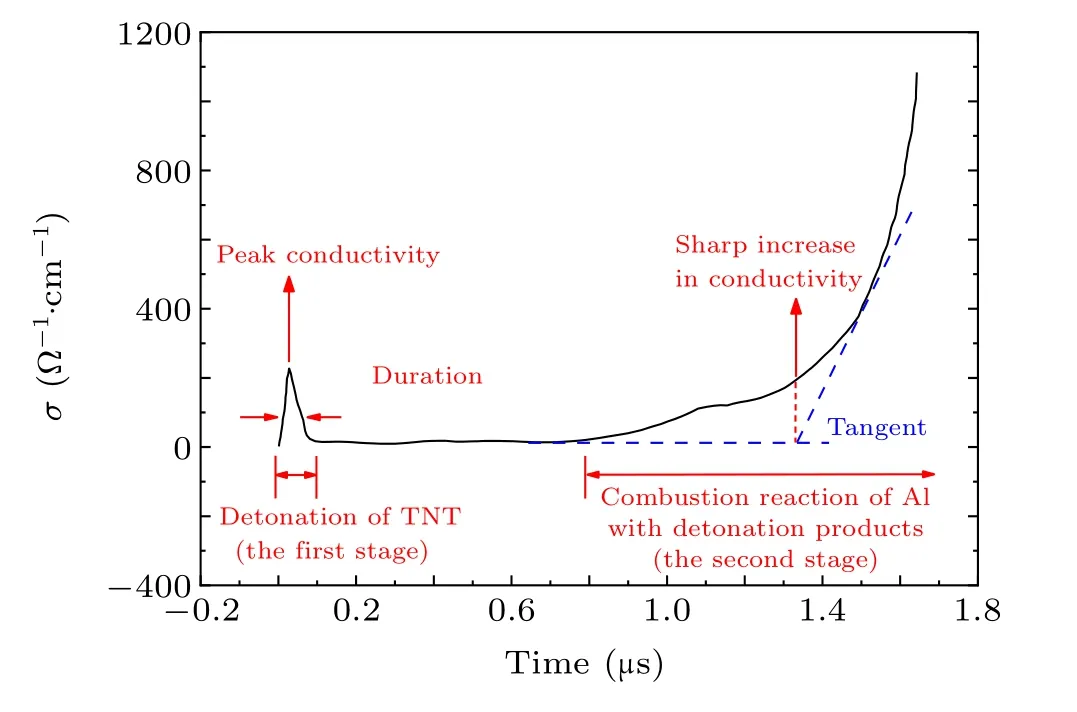
Fig.8. Typical results of conductivity experiments.[30]

It is evident from the typical test results of the conductivity test in Fig. 8 that the detonation of TNT/Al is divided into two stages. The first stage is the detonation reaction of TNT,i.e., C7H5O6N3→1.5N2+2.5H2O+3.5CO+3.5C.The second stage is the burning reaction of Al with the detonation products,i.e., Al+1.5H2O→0.5Al2O3+1.5H2,Al+1.5CO→0.5Al2O3+1.5C.[31]In the first stage,the TNT explosion process produces conductive free carbon,which increases the carbon content, and the conductivity increases sharply for the first time. In the second stage, Al begins to react with detonation products to form conductive media such as C and Al2O3, causing the conductivity to rise sharply for the second time. According to the results of the electrical conductivity experiments, the burn rate of aluminum in TNT/Al can be determined.

5. Results and discussion

In this study, combined with an improved conductivity test method proposed by Zhou,[29,30]the burn rate of aluminum powder in a detonation environment is studied for different system temperatures and aluminum particle sizes. The time corresponding to the peak value of the burn rate formula is calculated and compared with the results of the sharp growth time from the experimental conductivity.

5.1. Effect of combustion temperature on combustion characteristics

The equilibrium temperature between the main explosive and the aluminum powder after detonation can be calculated by the heat capacity method.[32]The corresponding detonation temperatures of the four different explosive contents(80%to 95%)are 3767 K,3602 K,3451 K,and 3309 K.

Using Eqs.(24)and(25), the burn ratio and burn rate of aluminum powder used in Ref. [30] can be calculated. The specific calculation results are shown in Figs.9-11.

Table 2. Comparison of the theoretical value at the peak time of aluminum powder burn rate and experimental value for the sharp growth time of electrical conductivity at different ambient temperatures.

Fig.9. Burn ratio and burn rate of aluminum particles at system temperatures of(a)3761 K,(b)3602 K,(c)3451 K,and(d)3309 K.

As the system temperature increases,the maximum burn rate of aluminum powder gradually increases,and the burning timetcgradually decreases. According to the relationship between the burn rate and time,the burn rate is lower at the start,and then increases rapidly. The reason for this is that as the surface of the aluminum particles is continuously vaporized,the particle size decreases, and the burn rate is inversely proportional to the particle size. This is the main reason for the increasing burn rate.

The calculation and experimental results are shown in Table 2. The results show that the difference between the theoretical calculation results and the experimental data for conductivity is less than 10%, indicating that the burn rate equation for aluminum powder has a good correspondence with the experimental data. However,the theoretical calculation value is smaller than the experimental value and the reason for this may be that the conductivity directly corresponds to the content of conductive carbon. After the combustion of aluminum and oxides containing carbon, carbon is produced. The process lags behind the combustion of aluminum powder, so the experimental value is relatively large.

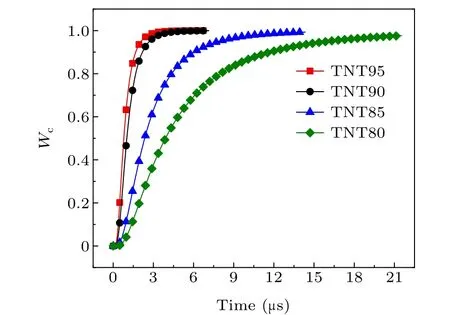
Fig.10. Burn ratio of aluminum powder at different system temperatures.

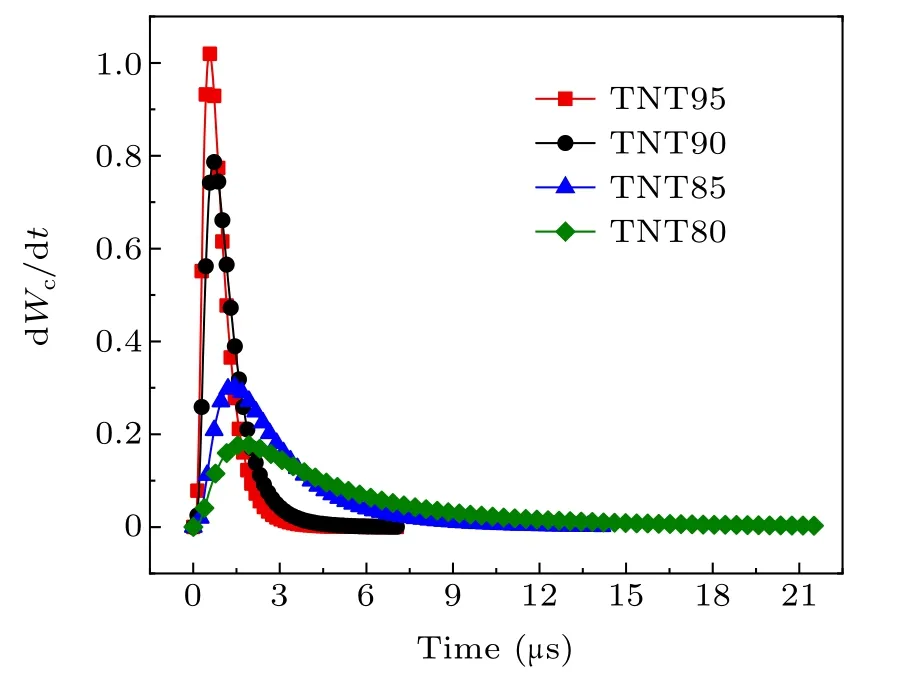
Fig.11. Burn rate of aluminum powder at different system temperatures.

5.2. Combustion equation of aluminum particles

The particle size of aluminum powder also has an important influence on the combustion characteristics of aluminum particles. To further study the influence of aluminum particle size on the burn ratio and burn rate under the same system temperature,combined with Ref.[29],this was calculated for aluminum powder with median diameters of 1.50µm and 9.79 µm at a system temperature of 3602 K. The calculation results are shown in Figs.12-14.

As seen in Table 3, when the particle size of aluminum powder increases,the maximum burn rate decreases and is delayed, and the burning time gradually increases. The difference between the theoretical calculation result and the electrical conductivity measurement data is within 15%.

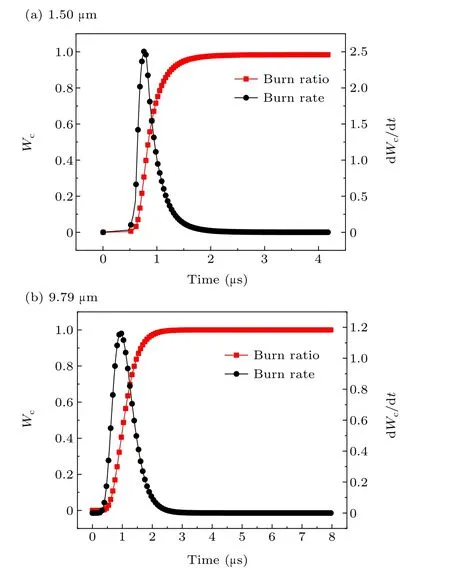
Fig.12. Burn ratio and burn rate of aluminum powder with particle sizes of(a)1.50µm and(b)9.79µm.

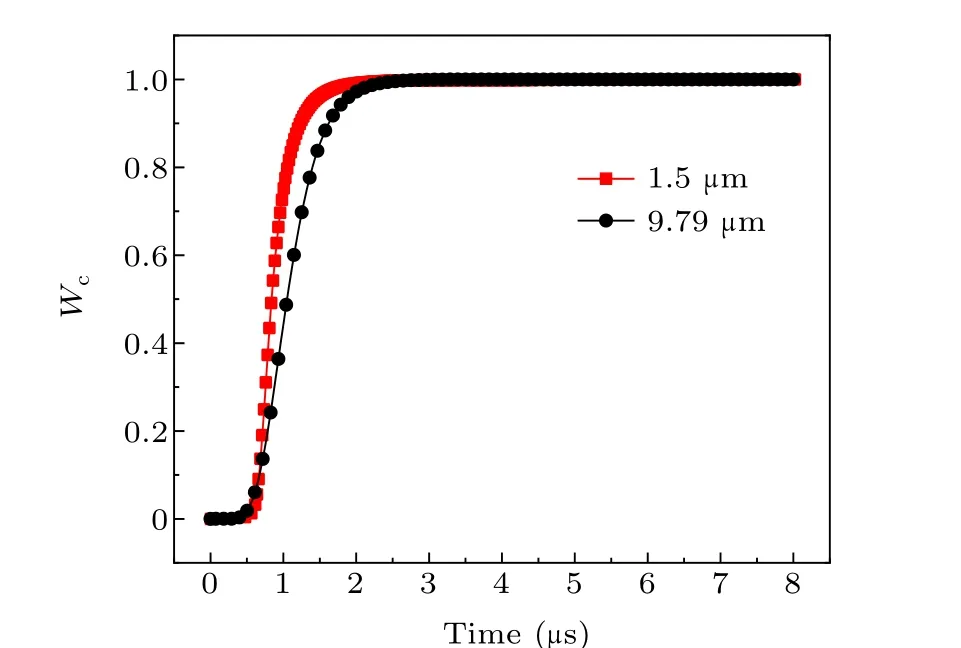
Fig.13. Burn ratio of aluminum powder with different particle sizes.

Fig.14. Burn rate of aluminum powder with different particle sizes.

Table 3. Comparison of theoretical values at the peak time of aluminum powder burn rate and experimental values for the sharp growth time of electrical conductivity under different particle sizes.

6. Conclusion

The combustion problem of aluminum powder after detonation wave is discussed. The established model and equation take into account the characteristics of high temperature,high pressure, and high-speed movement in detonation environment, which provides strong theoretical support for the study of the combustion of aluminum particle in detonation environment.

(i) A combustion model of aluminum particles in a detonation environment is established,and a combustion control equation of aluminum particles is theoretically deduced.It can be seen from the control equation that the burning time of aluminum particle is mainly affected by the particle size,system temperature and diffusion coefficient. The calculation result shows that a higher system temperature,larger diffusion coefficient and smaller particle size will lead to a faster burn rate and shorter burning time of aluminum particles.

(ii) Combined with the particle size distribution of the aluminum powder, the combustion control equation of aluminum powder is further established. The calculation results show that with increasing system temperature, the maximum burn rate of aluminum powder increases,and the burning time decreases. When the particle size of aluminum powder increases,the maximum burn rate decreases and is delayed,and the burning time gradually increases.

(iii)The difference between the time corresponding to the peak burn rate of aluminum powder obtained by theoretical calculation and the experimental electrical conductivity data is within 15%. This proves that this equation can be used to describe the combustion process of aluminum particle after detonation wave,and this equation can be used as a means to quantitatively describe the combustion behavior of aluminum powder in detonation environment.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.11772058).