Influence of various shapes of nanoparticles on unsteady stagnation-point flow of Cu-H2O nanofluid on a flat surface in a porous medium: A stability analysis

Astick Banerjee Krishnendu Bhattacharyya Sanat Kumar Mahato and Ali J.Chamkha

1Department of Mathematics,Sidho-Kanho-Birsha University,Purulia 723104,India

2Department of Mathematics,Institute of Science,Banaras Hindu University,Varanasi 221005,India

3Faculty of Engineering,Kuwait College of Science and Technology,Doha District,Kuwait

Keywords: Cu-H2O nanofluid, various shapes of nanoparticles, unsteady stagnation-point flow, dual solutions,stability analysis

1. Background of the investigati on

The boundary layer flow forms adjacent to the surface on which the fluid flows,so its dynamics and effect are too much important in fluid mechanics. While, the heat transfer in the boundary layer is responsible for cooling the surface and consequently,it is a handy tool for many industries. Now,in this era of science, the ultra-high cooling rate is one of the most crucial requirements of many engineering processes and industries, but the primary limitation is small thermal conductivities of traditional fluids, like, water, oil, ethylene glycol,etc. Previously, solid particles are added in traditional fluids to increase the inherently poor thermal conductivity of those traditional fluids and all efforts are centered on the mixing of micrometer-sized particles,but this approach has some technical shortcomings,such as micro-particles are rapidly deposited as a sediment in fluids,those may block the flow and cause an extra pressure drop. This problem can be settled by adding nanometer-sized particles, called nanoparticles, in aforesaid host fluids and the mixture is known as “nanofluid” proposed by Choi.[1]Adding nanoparticles with typical sizes less than 100 nm in host fluids drastically improves many thermal properties, especially, the thermal conductivities of the mixtures, i.e., nanofluids. To describe the motion of a nanofluid two models have been proposed, namely, “two-phase”, and“single-phase” by Buongiorno[2]and Tiwari and Das,[3]respectively. The Tiwari and Das model is more useful between the two for Newtonian base fluids. There are several types of nanoparticles,namely,metals,oxides,carbides,nitrides,or CNTs,which are normally used. Different nanoparticle types have different impacts on the enhancement of thermal conductivity. In addition to the type, the shape of nanoparticles is equally liable to the increase of effective thermal conductivity of the mixture. Maxwell[4]proposed a model for thermal conductivity of a solid-liquid mixture and based on his model the effective thermal conductivity is given by

whereκpis thermal conductivity of solid particle andκlis thermal conductivity of liquid. Maxwell’s model of effective thermal conductivity is based on the assumption that the solid particles are of a spherical shape. Later, Hamilton and Crosser[5]suggested a new model for effective thermal conductivity of the mixture as

wherem= 3/ψ∗represents the shape factor,ψ∗being the sphericity which is defined as the ratio of the surface area of the sphere having same volume to that of the solid particle, to the surface area of the solid particle. So, obviously for spherical-shaped particlesmis equal to 3, i.e., form=3,Hamilton and Crosser’s model becomes Maxwell’s model.Also, for some standard particle shapes, the values ofmare given in Table 1. These two models are independent of size of the solid particles and it means that these two are equally valid for mixtures having nano-sized particles. One can also find some other proposed models[6,7]to describe effective thermal conductivity. Detailed analysis of thermal conductivity of nanofluid with alumina nanoparticles and ethylene glycol base fluid was reported by Becket al.[8]considering various factors along with different shapes of particles.Timofeevaet al.[9]experimentally verified the effective thermal conductivity model by Hamilton and Crosser[5]using alumina nanoparticles and the hybrid base fluid consisting of water and ethylene glycol in 1:1 volume ratio. Later, Ellahiet al.[10]described the effect of different shapes of nanoparticles on entropy generation in MHD natural convection and Hamidet al.[11]discussed the rotating flow of nanofluid along a stretching sheet considering various shapes of MoS2nanoparticles. Some other important investigations on nanofluid with various shapes of nanoparticles may be found in the literature.[12-17]

Table 1. The values of shape factor for various shapes of nanoparticles.

A porous medium can be used to achieve an adequate cooling rate, i.e., usage of porous media may be treated as a technique for heat transfer enhancement. Porous media are solid materials that have interconnecting pores or voids. So,these are open cell, rigid, and saturated, which indicates that inter-connected pores in the medium are completely fliled with some fluid and that fluid may easily flow through the pores.Simultaneous use of both porous media and nanofluid is capable of grabbing substantial attention as new technique to achieve a satisfactory cooling rate with a wide range of applications. For porous media usage,the contact area between fluid and solid surface increases, whereas nanofluids cause enhancement in effective thermal conductivity of the mixture and these increase the rate of heat transfer. The treatment of nanofluids along with porous media has various beneficial applications, such as higher heat transfer, minimum clogging,miniaturization of system,size reduction of heat transfer system, and microchannel cooling, etc. The thermal instability of nanofluid flow in porous medium was investigated by Nield and Kuznetsov[18]taking the Darcy model and Kuznetsov and Nield[19]for the Brinkman model. Ahmad and Pop[20]simultaneously considered nanofluid and porous medium for mixed convection on vertical flat plate,whereas,mixed convection on a vertical wedge was discussed by Gorlaet al.[21]with similar consideration. Hatami and Ganji[22]took sodium alginate(SA)as a base fluid and titanium dioxide(TiO2)as nanoparticles to explore heat transfer characteristics for flow inside two coaxial cylinders in a porous medium. Xuet al.[23]discussed the forced convective nanofluid flow through foam metals in a duct and reported a pressure drop. Xu and Xing[24]numerically investigated natural convective nanofluids flow in a metal foam cavity using the lattice Boltzmann(LB)model. Convective heat transfer in nanofluid flows in foam metals was studied by Xuet al.[25,26]with the local thermal non-equilibrium(LTNE) effect. Later, Xuet al.[27]described, in detail, various modes of heat transfer for nanofluid flow in a porous medium. Mehryanet al.[28]illustrated the flow of magnetic hybrid nanofluid inside a double-porous medium. Recently,Ros¸caet al.[29]studied stagnation-point flow of nanofluid towards a vertical plate.

Motivated by the engineering requirement of strong cooling rate and by the fact that nanofluid and porous medium together could be able to fulfill the requirement very efficiently,here we investigate the unsteady stagnation-point flow of Cu-H2O nanofluid on a flat surface in a porous medium taking effect of various shapes of nanoparticles. Viscous dissipation and thermal radiation effects are also considered. This study will explore how the shapes of the nanoparticles play a significant role in controlling heat transfer,i.e.,the cooling rate along with other physical parameters. This type of stagnation-point flow problem has many applications, like, the cooling of nuclear reactors and electronic devices,heat exchangers located in a region having small-velocity, solar pond, oil extraction and transportation,photo-catalysis,etc.

2. Problem formulation and basic equations

Consider the unsteady boundary layer flow near a stagnation-point in Cu-H2O nanofluid over a flat plate embedded in porous medium. The external stagnation-flow velocity is assumed to vary linearly in the form ofue(x,t) =ax(1-ct)-1, wherea(＞0) andcare constants. The wall temperatureTwis assumed variable. Asyattends to infinity,the value of temperature reaches to a constant valueT∞. In addition,the viscous dissipation effect and thermal radiation are considered. Under these assumptions, along with the boundary layer structure,the governing equations are

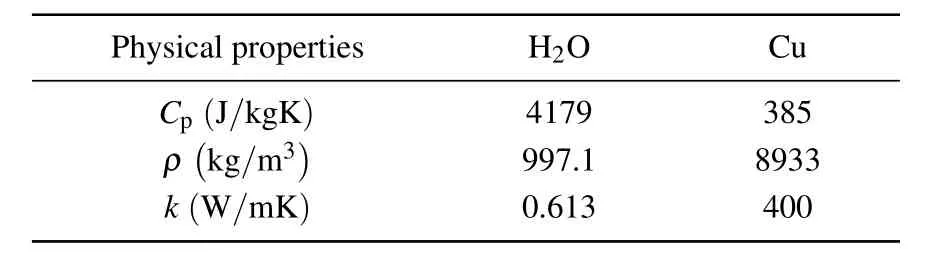
Table 2.Thermophysical properties of fluid and nanoparticles(Oztop and Abu-Nada[30]).

The transformed boundary conditions in Eq.(5)are

3. Solution methodology and its validation

The coupled nonlinear Eqs. (10) and (11) with Eq. (12)constitute a BVP and the BVP is numerically solved by a shooting method by converting it into an IVP.We are omitting details of the method,[33-39]which is already available in the literature. To confirm the accuracy of the numerical scheme and computational results,the values off＇＇(0)forφ=0.1 andK=0 are compared with the published results of Bachoket al.[40]and Salemet al.[41]in Table 3 and the results are found in brilliant agreement. In addition,a graphical comparison of velocity profiles forA=-0.5 withφ=0 andK=0 with the results of Bachoket al.[40]is performed in Fig. 1 and those profiles are observed to have an excellent match.

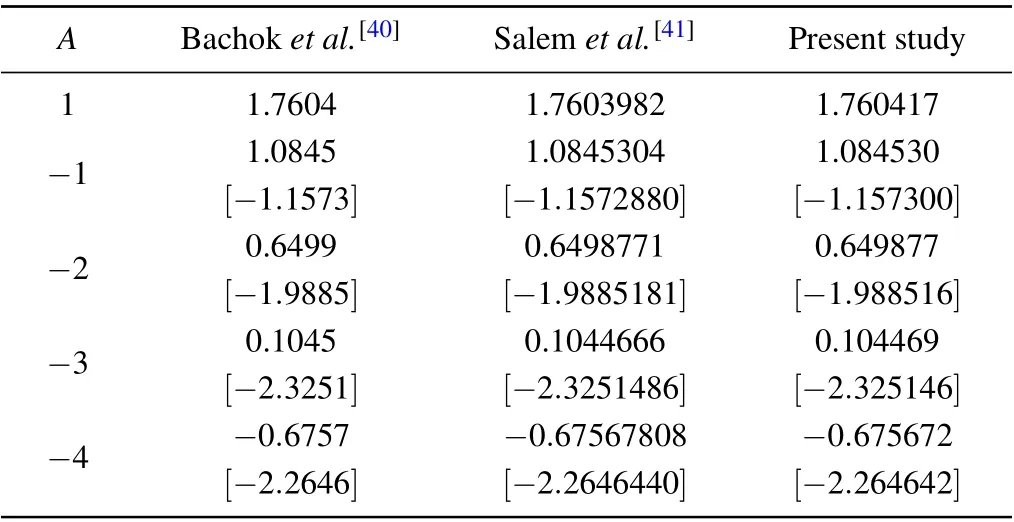
Table 3. Comparison of the values of f＇＇(0) for different values of A with φ =0.1 and K=0.

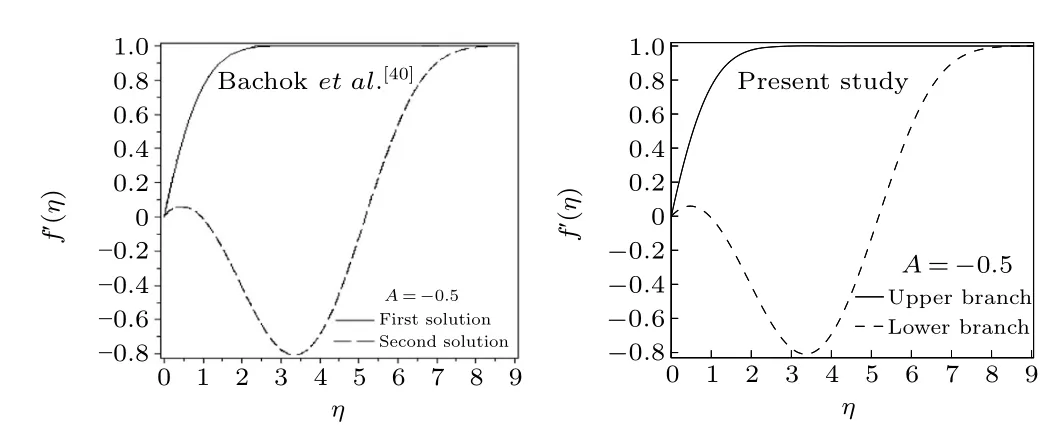
Fig.1. Comparison of velocity profiles for A=-0.5 with φ =0 and K=0.

4. Results and discussion

To know the impact of nanoparticles and its various shapes in controlling heat transfer in the unsteady stagnationpoint flow of Cu-H2O nanofluid on a flat surface in a porous medium, the numerically computed results of various physical properties are presented in Figs.2-18 for different values of involved parameters, namely, the unsteady parameter (A),nanoparticle volume fraction(φ),shape factor of nanoparticles(m),permeability parameter(K),radiation parameter(R),and the Eckert number (E) with the Prandtl number being taken as 6.13 (water) throughout the computations. The volume fraction of nanoparticles is considered 0 and 0.1,whereφ=0 represents the water without any nanoparticle. Results for skin friction coefficient and the Nusselt number demonstrate the existence of dual solutions for any value of decelerating unsteady parameter(A ＜0). But the dual solutions exist up to a certain critical value (say,Ac＜0) of decelerating unsteady parameter and beyond that critical value(A ＜Ac)there is no self-similar solution. Whereas, for accelerating unsteady and steady cases (A ≥0), the solution is single, i.e., unique. Due to decelerating unsteadiness of the flow dual solutions exist.The negative value of the unsteady parameter means that the constantctakes a negative value and it is the coefficient of the time variable. It consequently implies that for decelerating unsteadiness, the impact of the time variable on the flow dynamics is completely opposite and it creates a situation of uncertainty as time progresses. Therefore, dual solutions of the flow dynamics are witnessed for decelerating unsteadiness. On the other hand, the presence of nanoparticles only does not affect the critical value,Ac,[40]but if the medium of flow is a porous medium, then the nanoparticles’presence disturbs the critical value for the existence of dual solutions and so we can accept this as an important finding of the investigation. When the nanoparticle volume fraction is 0.1 then critical valueAcis-5.9135 forK=0.5 and whenφ=0,Acis-6.4843 forK=0.5 (Fig. 2). It directly means that in a porous medium the nanoparticles cause the reduction in the magnitude ofAc,i.e.,the range of existence of dual solutions reduces when nanoparticles are added to the flow field. It is also worth noting that the shapes of nanoparticles have no impact on the aforesaid existence range of dual solutions. In addition, for a unique solution and upper branch solution the drag force enhances due to the presence of nanoparticles for accelerating the unsteady parameter and some cases of decelerating the unsteady parameter. While in the lower branch solution the drag force reduces due to nanoparticles for all values of decelerating the unsteady parameter except near the zero value.Restriction on the surface drag force is very crucial in application viewpoints because the drag force is imposed on the solid surface. In Fig. 3, the Nusselt number is plotted for different shapes of Cu-nanoparticles, i.e., different values of shape factormand it is witnessed that asmincreases the Nusselt number also increases, i.e., the cooling rate enhances withm. The shape factor is inversely proportional to the sphericity, i.e., the ratio of the surface area of the sphere having equal volume to that of nanoparticle,to the surface area of the nanoparticle. So, asmincreases, sphericity decreases,i.e., the surface of the nanoparticle is large and hence the heat-carrying capacity of the nanoparticle becomes higher. As a consequence, the cooling rate is higher whenmhas larger values. So, the nanoparticles in the form of blades are the best for the heat transfer nanofluid when it is compared with the other shapes (spheres, bricks, cylinders, and platelets) of nanoparticles. Therefore, in many engineering and industrial processes related to heat transfer, blade shape nanoparticles are more beneficial than other shapes considered and so, the shape of nanoparticles can control the heat transfer and hence the final quality of the product.The permeability of the porous medium has a strong influence on the existence range of dual solutions, i.e., on the critical value,Ac(Fig. 4). The range of existence of dual solutions is wider when the permeability parameter is larger. The values ofAcare-4.5066,-5.9135,and-7.4581 forK=0,K=0.5,andK=1. The permeability parameter is inversely proportional to the permeability of porous material. So,asKincreases the permeability of porous medium becomes less, i.e., the Darcy resistive force due to porous medium is larger and it results in a significant augmentation of the range of existence of dual solutions. For the same reason,the drag force,i.e.,the skin friction coefficient is noticeably high with the permeability parameter in the upper branch solution and unique solution. For different values ofK, the Nusselt number is plotted for all considered values of shape factorm,i.e.,for various shapes of Cu-nanoparticles in Fig. 5. For the upper branch solution, the Nusselt number,i.e., the cooling rate rises withKfor all shapes of considered Cu-nanoparticles and physically,it is the consequence of less permeability of the porous medium. For less a permeable porous medium,i.e.,for a more compact porous medium though momentum transport obstructed,but it is quite suitable for high heat transport. So, this very high heat transfer rate due to porous medium in the nanofluid flow has colossal applications in many industrial and engineering problems,like the cooling of electronic devices, the cooling of metallic sheets,etc., while in the lower branch the contrasting effect is witnessed. The impact of the radiation parameter and the Eckert number on the cooling rate, i.e., the Nusselt number, are depicted in Figs.6 and 7,respectively. The cooling rate is higher for larger values of the radiation parameter. It implies that as the thermal radiation level is high the cooling rate raises and physically this is the excepted outcome. Whereas,a non-zero Eckert number cooling rate slightly reduces for many cases of decelerating unsteady flow and for accelerating unsteady flow a minute enhancement in cooling rate is observed. Moreover,in Fig.8 the Nusselt number is plotted withRfor differentEandm. It reveals that the effect of the Eckert number on heat transfer coefficient is less prominent with the rise of radiation and the radiation has a considerable impact on heat transfer for different-shaped nanoparticles. Radiative heat transfer is very effective,like convective heat transfer in the presence of nanoparticles.

Fig. 2. Skin-friction coefficient, CfrRe1/2x with A for different nanoparticle volume fractions.

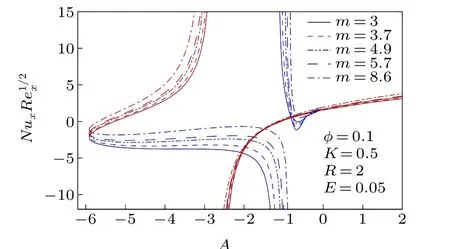
Fig. 3. Nusselt number, NuxRe-1/2xwith A for different shapes of nanoparticles.

Fig.4. Skin-friction coefficient,CfrRe1/2x with A for different values of K.

Fig.5. Nusselt number,NuxRe-1/2xwith A for different values of K.

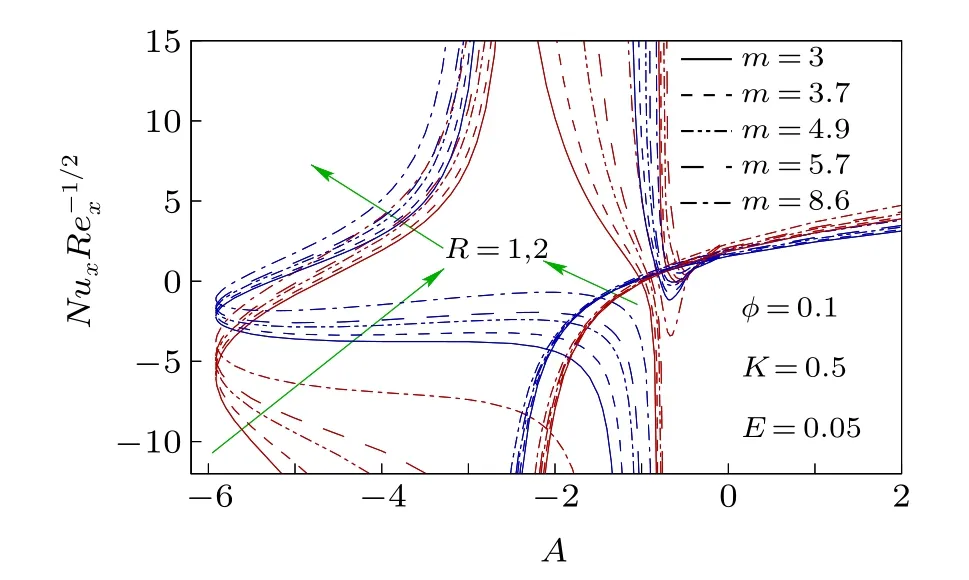
Fig.6. Nusselt number,NuxRe-1/2xwith A for different values of R.

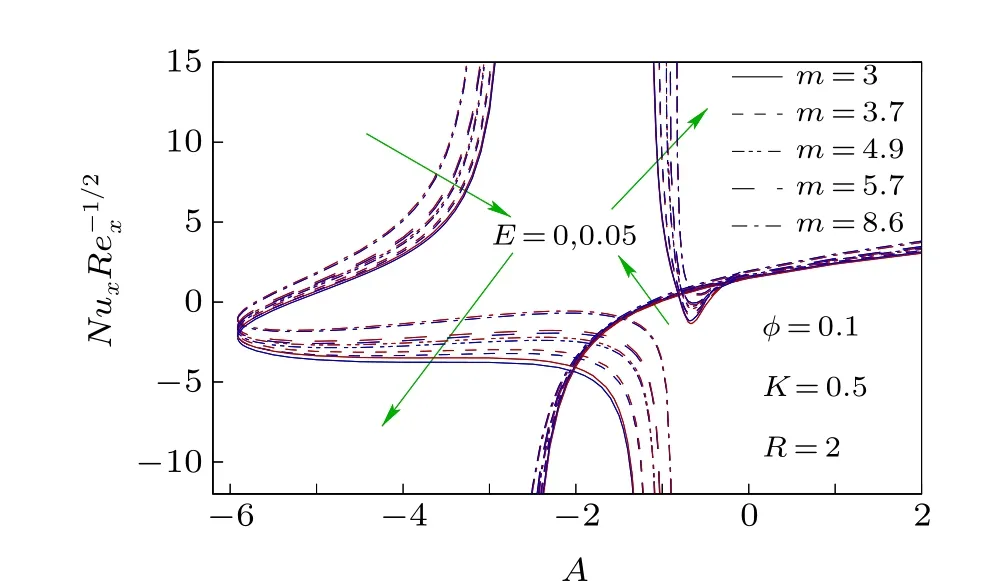
Fig.7. Nusselt number,NuxRe-1/2xwith A for different values of E.

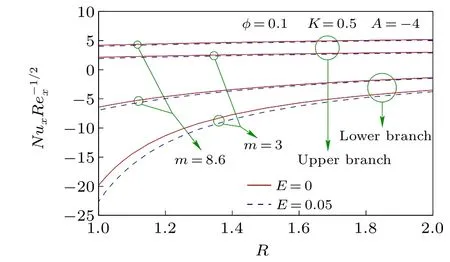
Fig.8. Nusselt number NuxRe-1/2xwith R for different values of E.

For different values of Cu-nanoparticle volume fractionφ, the velocity profiles are shown in Fig. 9. For both solution branches,in spite of initial decay in velocity the boundary layer thickness(BLT)is reduced withφ. Due to the nanoparticle presence the intermolecular force increases and as a consequence, the free stream velocity is achieved earlier and it causes the decline of BLT.In Fig.10, the temperature profileθ(η) is plotted for all considered values of shape factorm.It exhibits an early decrease of temperature and an increased thermal BLT withm. In reality,the high heat transfer rate with largerm(due to larger surface area)affects free stream temperature up to a longer distance from the flat surface and therefore thermal BLT becomes thick.

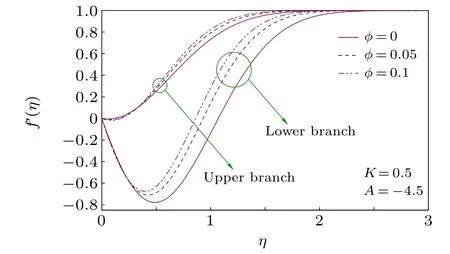
Fig.9. Velocity profiles for different nanoparticle volume fractions.

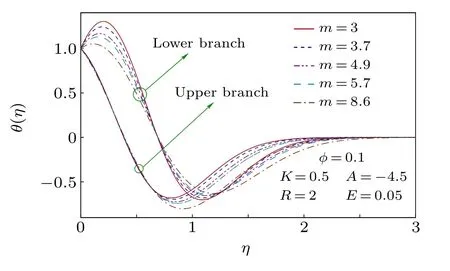
Fig.10. Temperature profiles for different shapes of nanoparticles.

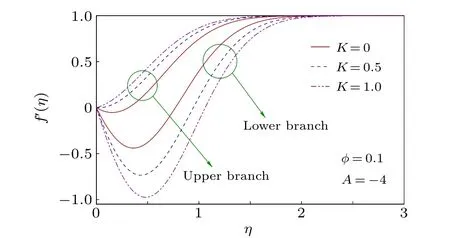
Fig.11. Velocity profiles for different K.

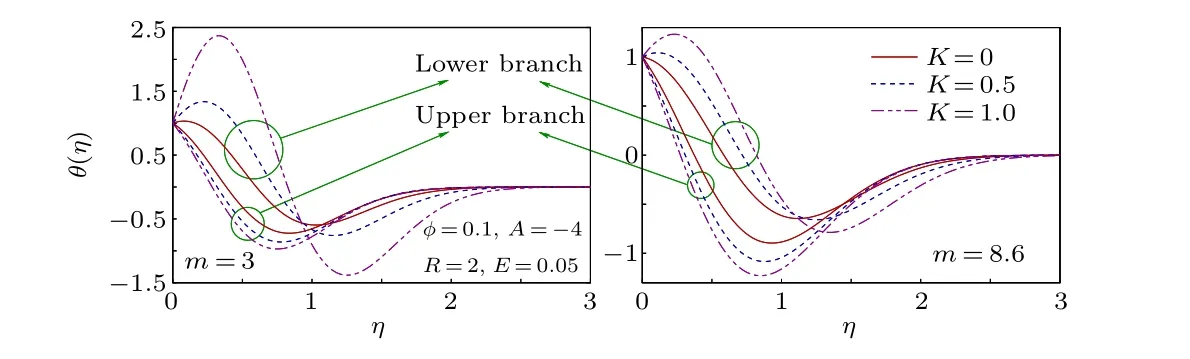
Fig.12. Temperature profiles for different K.

The impact of permeability parameterK(related to the permeability of the porous medium)on the nanofluid velocity and temperature profiles are illustrated in Figs. 11 and 12. It exhibits contrasting effects on two solution branches. In the upper branch solution,the velocity rises withKand BLT turns out to be thinner. The Darcy resistive force in porous medium is inversely proportional to its permeability and therefore,with the rise ofK,i.e.,with a medium having less permeability,this force grows. Consequently,a shrink of BLT occurs. Whereas the temperature(plotted for two values ofm)inside the boundary layer shows a decay withKin the upper branch and lower branch temperature exhibits an initial rise, while away from the surface,the reverse result is found.

Fig.13. Velocity profiles for different A(＜0,decelerating unsteady flow).

Fig.14. Velocity profiles for different A(＞0,accelerating unsteady flow).

The nanofluid velocity profiles are displayed in Figs. 13 and 14 for decelerating and accelerating unsteady flows. Due to increasing magnitude of decelerating unsteady parameter(A ＜0), the flow velocity reduces in the upper branch solution and it increases with accelerating unsteady parameter(A ＞0). Decelerating unsteadiness of the flow creates such a situation,for which dual solutions exist and no other parameter can control this uncertain situation of the flow. It is already witnessed that the Darcy force of porous medium increases the region of uncertainty of dual solutions. Whereas accelerating unsteadiness is natural and has no ambiguous property, like decelerating unsteadiness and consequently, the solution becomes unique. In Figs. 15 and 16, the nanofluid temperature profiles are presented for various values ofA. For decelerating unsteady flow, the temperature rises with increasing magnitude ofAin the upper branch with thermal BLT being thinner and though the initial behavior is the opposite for the lower branch,thermal BLT reduces with a magnitude ofA. Whereas the nanofluid temperature decreases withAin unique solution for accelerating unsteady flow.

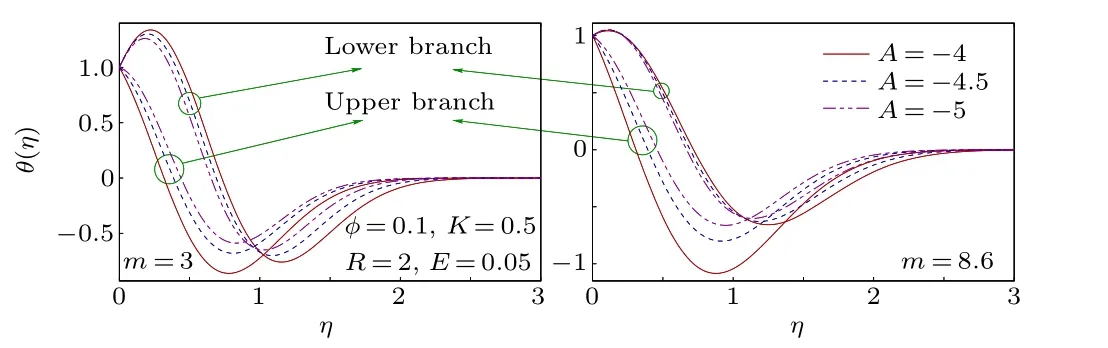
Fig. 15. Temperature profiles for different A (＜0, decelerating unsteady flow).

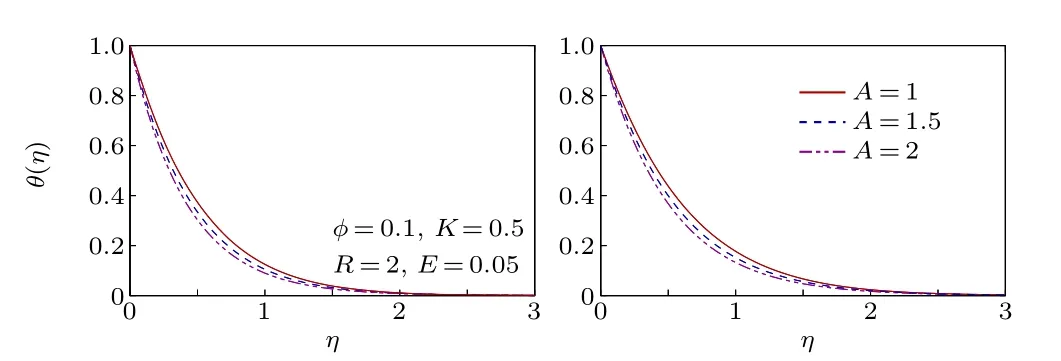
Fig. 16. Temperature profiles for different A (＞0, accelerating unsteady flow).

The nanofluid temperature profiles are depicted in Figs. 17 and 18 for different values of the radiation parameter and the Eckert number,respectively. For thermal radiation,the thermal BLT is expanded and it takes place because the radiative heat transfer disturbs the temperature in a free stream for a longer distance from the flat surface. The growth of thermal BLT is meaningfully large for blade-nanoparticles and so this thermal BLT expansion due to radiation is crucial in several engineering processes,like seawater desalinization,solar thermal chemical reaction and combustor,[27]when the choice of shape of the nanoparticles is made. For growth in the Eckert number, the temperature inside nanofluid boundary layer shows an increasing trend.

Fig.17. Temperature profiles for different R.

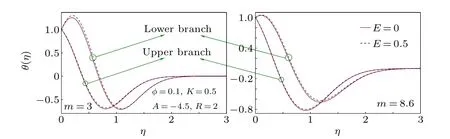
Fig.18. Temperature profiles for different E.

5. Stability analysis of obtained solutions

Due to the existence of dual solutions for a specific range of unsteady parameter (for decelerating unsteady flow) along with a unique solution (for steady and accelerating unsteady flow),it becomes necessary to check the stability of those solutions. So, a stability analysis is performed following Weidmanet al.[42]and Bakaret al.[43]A new dimensionless similarity variableτis introduced and the similarity solutions are taken as

Equations(23)and(24)with Eq.(25)constitute an eigenvalue problem withγan eigenvalue, to be determined. An infinite set of eigenvaluesγ1＜γ2＜γ3＜···will be obtained on solving the eigenvalue problem(23)-(25). The least eigenvalueγ1will regulate the stability of the solutionsf(η)andθ(η). Ifγ1has a positive value,then there will be an initial decay of disturbances to the solutions and in this case, the solutions will be stable. Now,ifγ1has a negative value,then there is a clear indication of initial growth of disturbances to the solutions and hence the solutions will be unstable.

After solving the above eigenvalue problem, the smallest eigenvaluesγ1are listed in Table 4 for upper and lower branch solutions(Ac≤A ＜0,decelerating unsteady flow)and the unique solution (A ≥0, steady and accelerating unsteady flow)for some values ofAwithφ=0.1 andK=0.5. The values ofγ1for the upper branch solution and the unique solution are found to be positive, while for the lower branch solution its value is negative. So, from the aforesaid analysis, it may be resolved that the upper branch and unique solutions are stable solutions,whereas the lower branch solution is an unstable solution. The stability or instability of solutions is not able to guarantee its physical existence or non-existence in real experiments. If an experiment is performed, then there will be two possibilities for decelerating unsteady flow(0＞A ≥Ac).There may be a real and visible boundary layer flow or no boundary layer formulation in the flow field. It means that when a stable solution occurs, it will be real and visible and when an unstable solution arises, it will have no physical existence,i.e.,due to many unavoidable disturbances during the experiment it will not be physically realizable. So, we may say that both solutions have physical meaning and relevance.

Table 4.Smallest eigenvalue,γ1 for some values of A with φ =0.1 and K=0.5.

6. Concluding remarks

The unsteady stagnation-point flow of Cu-H2O nanofluid on a flat surface in a porous medium is investigated taking effects of various shapes of Cu-nanoparticles.The effects of viscous dissipation and thermal radiation are taken into consideration. The governing equations of the problem are converted into self-similar coupled ODEs which constitute a BVP and it is solved by a shooting method. After a complete analysis, a summary of findings is as follows:

(i) Dual solutions exist for any value of the decelerating unsteady parameter(A ＜0),i.e.,decelerating unsteady flow and these solutions exist up to a certain critical valueAc(＜0). Whereas, for accelerating unsteady and steady flows(A ≥0),the solution is unique.

(ii) Only the presence of nanoparticles does not affect the value ofAc, but when flow is considered in a porous medium then the magnitude ofAcdecreases with nanoparticle volume fraction. Also,due to larger permeability parameter,the range of existence of dual solutions is longer.

(iii) The shapes of nanoparticles have no influence on the value ofAc, but it has a huge impact on surface heat transfer.

(iv) The Nusselt number,i.e.,the cooling rate enhances with increasing values of shape factormand the presence of thermal radiation. Also,for upper branch and unique solutions,the drag force and cooling rate rise withK.

(v) For the positive Eckert number,a minor reduction in the cooling rate is observed in some cases of decelerating unsteady flow and for the accelerating unsteady flow a contrasting effect is found.

(vi) For the upper branch solution, the velocity rises withKalong with a reduction in BLT and the opposite nature exhibits for the lower branch. Whereas,despite an initial decay of temperature,the thermal BLT enhances withm.

(vii) For decelerating unsteady flow(A ＜0),velocity reduces in the upper branch and it increases for accelerating unsteady flow (A ＞0). Opposite trends are observed in temperature.

(viii) After the stability analysis, it is obtained that the upper branch and unique solutions are stable, whereas the lower branch solution is unstable.