Acoustic radiation force on a rigid cylinder near rigid corner boundaries exerted by a Gaussian beam field

Qin Chang(常钦) Yuchen Zang(臧雨宸) Weijun Lin(林伟军)Chang Su(苏畅) and Pengfei Wu(吴鹏飞)

1Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China

2University of Chinese Academy of Sciences,Beijing 100049,China

3Beijing Deep Sea Drilling Measurement Engineering Technology Research Center,Beijing 100190,China

Keywords: acoustic radiation force,finite element method,Gaussian beam field,acoustic manipulation

1. Introduction

As the fundamentals in biomedical ultrasound, material science and other fields, acoustic radiation force has become hotspots in acoustic tweezers,[1,2]and acoustic levitation,[3]etc. Since King[4]first proposed the concept of acoustic radiation force for particles and figured out an analytical expression for the acoustic radiation force of a rigid sphere in the ideal fluid in 1934, scholars have developed many models to describe the acoustic radiation force of the particles in various acoustic fields.[5-21]In earlier researches, particles were usually defined as ideal geometries(cylinders or spheres)with simple solid mechanical properties(rigid or elastic)and these particles were commonly supposed to be suspended in a free acoustic field. However, in many practical applications, the walls of the container are more diverse and ignoring the influence will cause errors. For example, a round-bottomed flask can be regarded as a combination of two:a sphere and a cylinder, and the connection between two parts can be treated as a transition from a cylinder to a sphere. If researchers intend to solve the acoustic radiation force on a particle moved from the bottom of the flask to the top,the calculation will be difficult but critical when the particle goes through the connection.Therefore,researchers tried to study effects of the boundaries on the acoustic radiation force.

In 1994, Guanauard[22]calculated the acoustic scattering of a sphere near a plane boundary firstly. Later, Huang and Guanauard[23]computed the scattering of a plane acoustic wave by a spherical elastic shell near a free surface.On the basis of Guanauard’s research,Miriet al.[24]analyzed the effect of a porous wall on the acoustic radiation force for contrast agent shells in detail. Wanget al.[25]theoretically and numerically studied the acoustic radiation force exerted by a standing wave on a rigid cylinder near a flat wall. Qiaoet al.[26-30]systematically studied the acoustic radiation force on cylindrical particles near an impedance boundary for both plane waves and Gaussian beam fields. More recently, our group extended Qiao’s results to the case for a 3D spherical shell near the interface.[31]

In fact,for the limitation of calculation method,it is hard to process transmission and reflection between particles and complex boundaries manually. However, benefiting from the development of analysis software, utilizing the computer to compute the acoustic radiation force via simulating the scattering sound field seems to be an effective method. In this investigation,a 2-D acoustic model is built by a finite element method(FEM)software and most of the calculations are performed by computer. In this model, there is a rigid corner boundary and a rigid cylindrical particle near the boundary in a Gaussian beam field. The spatial positions of geometries are adjustable,such as the angle between two rigid boundaries and the distances between particle and boundaries. In addition, particular emphases are paid to the beam frequency, the incidence angle,and the beam waist radius. It is convenient to study the effects of boundaries on the acoustic radiation force by changing the parameters. On the basis of studies on the rigid corner case, a demonstration of calculating the acoustic radiation force exerting on a rigid cylindrical particle immersed in fluid near a rigid circular corner is briefly introduced to verify the universality of the FEM model.

2. Method

2.1. Theoretical analyses

As shown in Fig.1,a corner is full of fluid with two rigid boundaries forming an angleα. A rigid cylindrical particle immersed in the fluid is perpendicular to theX-O-Yplane near by the corner,d1andd2represent the distance from the central of particle to boundary 1 and boundary 2,respectively.A weakly focused Gaussian beam field is incident upon the particle,whereφrepresents the angle between the beam axis and theX-direction.

Fig. 1. The 2D acoustic model used to calculate the acoustic radiation force on a rigid cylindrical particle near a rigid corner immersed in water.

2.2. Theoretical analyses in the case of right angle

Partial wave series expansion method(PWSEM)is a classical method to analyze the acoustic radiation force. When the two flat boundaries form a right corner,it is convenient to deal with the problem analytically based on the image method.Three image cylinders are placed at the symmetrical positions to equate the effects of boundaries. The incident wave in thejth coordinate system is expressed in the coordinate system of thepth cylinder as

An object will experience a mean force,known as acoustic radiation force, when subjected to a harmonic-continuous sound field.Considering that the surrounding fluid is ideal and cannot absorb any momentum from the sound wave,the acoustic radiation force can be computed by integrating the radiation stress tensor over a circular cylindrical surfaceS0enclosing the cylinder.It has been proved to be advantageous to evaluate the radiation force using the far-field scattering,which can be expressed as[32]

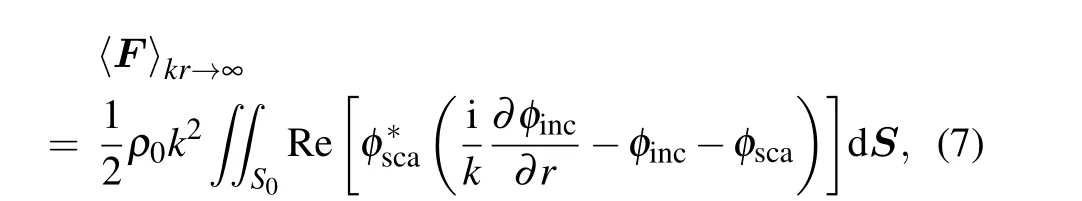
where dS= dSerwith dS=Lrdθbeing the scalar differential element of a cylindrical surfaceSin lengthLtaken at a large radiusrenclosing the cylinder, the outward unit vector iser=cosθex+sinθey, withexandeybeing the unit vectors in the coordinate systemxOy,Re denotes the real part of a complex function,the superscript∗denotes the complex conjugate of a complex function, and the symbol〈〉represents time averaging.

Projecting Eq. (7) into thexandyaxes, we can obtain the expression of the two component radiation forces,respectively,as

2.3. Numerical model

Based on the simplification from the tensor integral approach,YxandYyare defined as

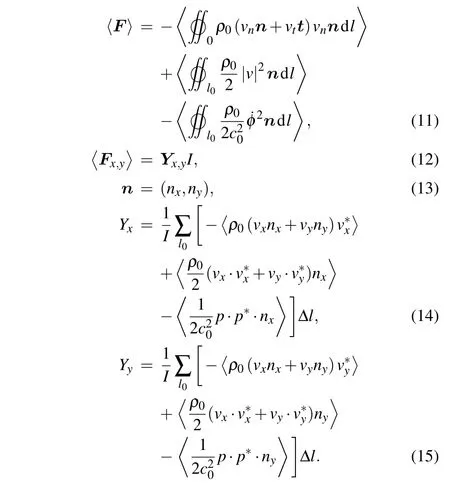
The values ofYxandYycan be calculated by Eq.(14)and(15),if the parameters of medium and the scattering sound field are known.

In this study, the acoustic pressure and particle velocity distributions in the fluid medium are calculated by COMSOL Multiphysics (version 5.6, COMSOL AB, Stockholm, Sweden). COMSOL is one of the most commonly used FEM software in acoustics,optics,electromagnetics,mechanics and other relevant fields.In the acoustics module(Pressure Acoustics,Frequency Domain)of COMSOL,the total acoustic pressure fieldPtis caused by the superposition of background pressure fieldPband scattered acoustic pressure fieldPs, and the total velocity is described by its root-mean-square valuevrms.The acoustic radiation force is considered to be induced by acoustic scattering, which is due to the momentum transfer between the acoustic wave and the particle.Psandvrmsare calculated by computer.Pbis the external incident Gaussian beam field.

As shown in Fig. 2, the calculated domain is comprised of a fluid domain and a perfectly matched layer (PML) domain. The PML domain is used to absorb the acoustic waves at the edge of the fluid domain. The corresponding parameters are clearly listed in Table 1. Especially,the radius of scatterer particleais a constant in this research.

Fig. 2. The FEM model used to calculate the acoustic radiation force on a rigid cylindrical particle near a rigid corner immersed in water.

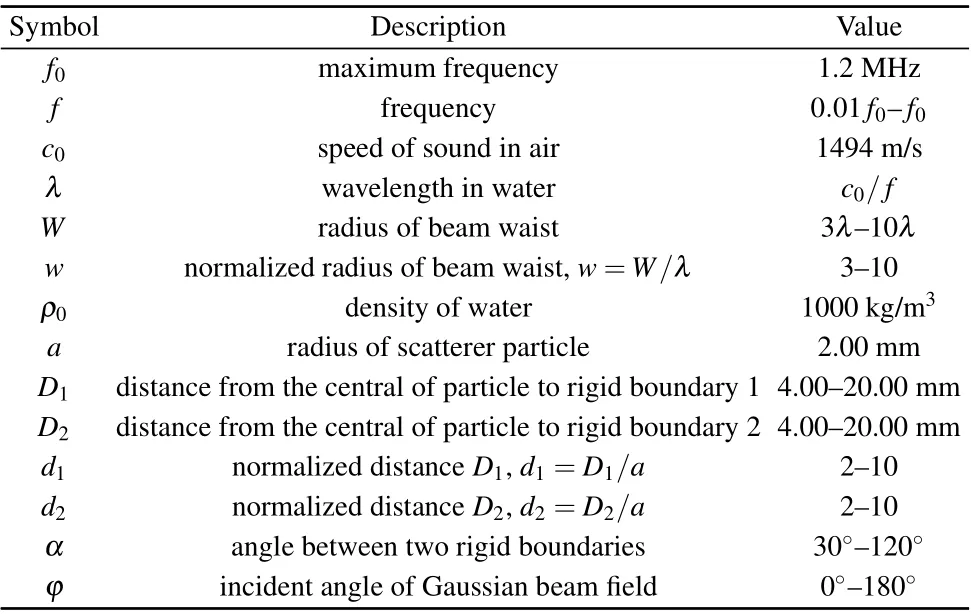
Table 1. Parameters used for the simulation.

After executing the Mesh module,the geometry is divided into plenty of area elements and then computer will process the model on the basis of meshes by execute the Study module.Figures 3 and 4 show the meshes and the total acoustic pressure field of a sample generated by COMSOL.In this sample,f=1.2 MHz,w=3,α=120°,φ=60°,andd1=d2=6.

Fig.3. The meshes for the sample divided by COMSOL.

Fig. 4. The total acoustic pressure field Pt for the sample calculate by COMSOL.

3. Numerical calculations and analyses

The axial acoustic radiation force function componentYpon a rigid cylinder in free space exerted by a plane wave is one of the most classical model and the results have been verified by many researchers. A comparison between the theoretical results of PWSEM and the numerical results of FEM to figure out the accuracy of the numerical model is shown in Fig. 5.The maximum absolute error is 0.0229 and the correlation coefficient between PWSEM and FEM is 0.9994,which can verify the reliability of the FEM model.

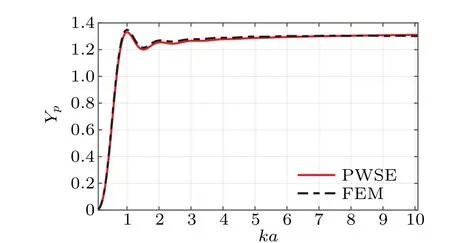
Fig. 5. The axial acoustic radiation force function component Yp on a rigid cylinder in free space exerted by a plane wave.

In theoretical researches, the 2D Gaussian beam field is defined as

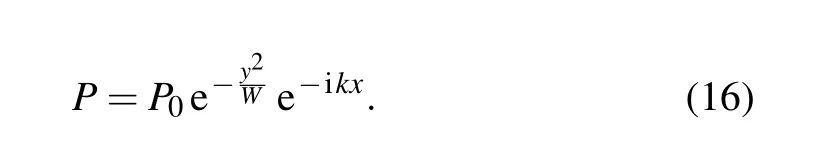
It is worth noting that a weakly focused Gaussian beam field emitted from a transducer cannot be described by Eq.(16)because the phase variety is ignored. In this case, the weakly focused Gaussian beam field only remains a half as shown in Fig.6.

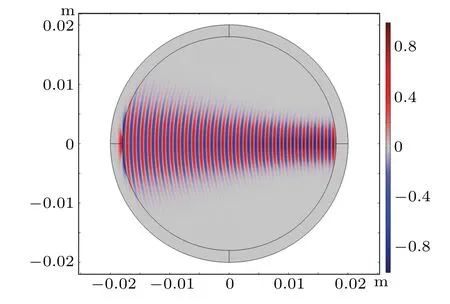
Fig.6. A phase-ignored weakly focused Gaussian beam field simulated by COMSOL.

In this investigation, the weakly focused Gaussian beam field is considered to be back to the original 2D Gaussian beam in optics:

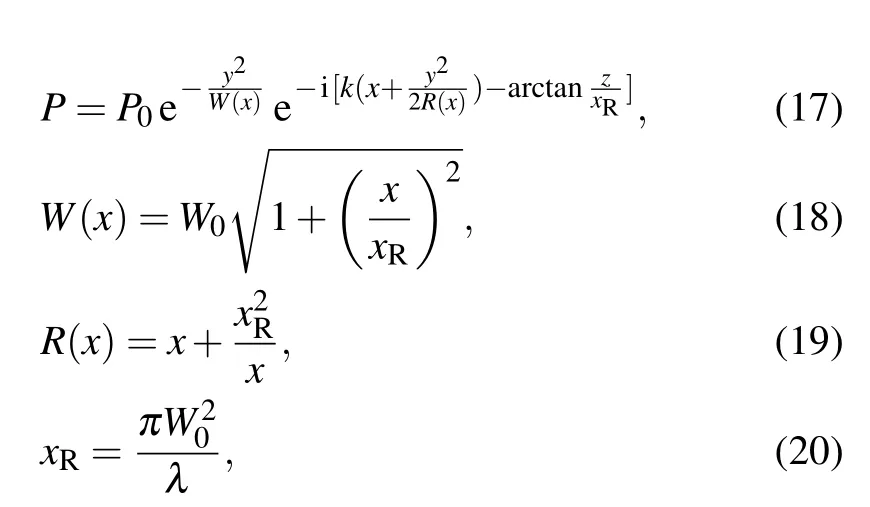
whereW(x)is the Rayleigh radius in optics that is often substituted by the radius of beam waistW0in acoustics,xRis the Rayleigh range,andR(x)is curvature radius. The relationship of these parameters is shown in the Fig. 7. Equation (17) is confirmed to be more realistic than Eq.(16)because the Gaussian beam field defined by Eq.(17)can describe the complete Gaussian beam field correctly. The correct Gaussian beam field is shown in Fig.8.

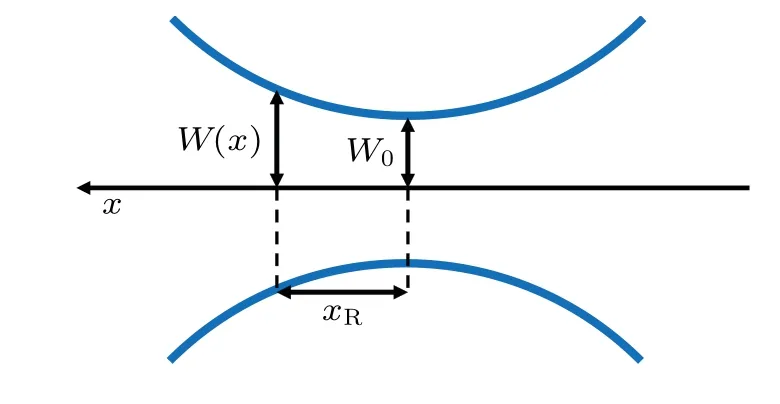
Fig.7. An optical Gaussian beam.

Fig.8. An optical Gaussian beam.

Because of the different expressions of Gaussian beam field,it is necessary to check the applicability of Eq.(17). The result of the axial acoustic radiation force function componentYpon a rigid cylinder in free space exerted by an optical Gaussian beam is shown in Fig.9. Whenkaincreases,Ypdecrease asaincreases. However,according to the results of PWSEM studied by many researchers,if thekais defined,there will be no direct relation betweenYpanda. This phenomenon suggests that Eqs. (16) and (17) are approximate only in a certain range (a=2-3 mm). In this research,ais finally set as 2.00 mm for the comparison with the theoretical results from other studies.

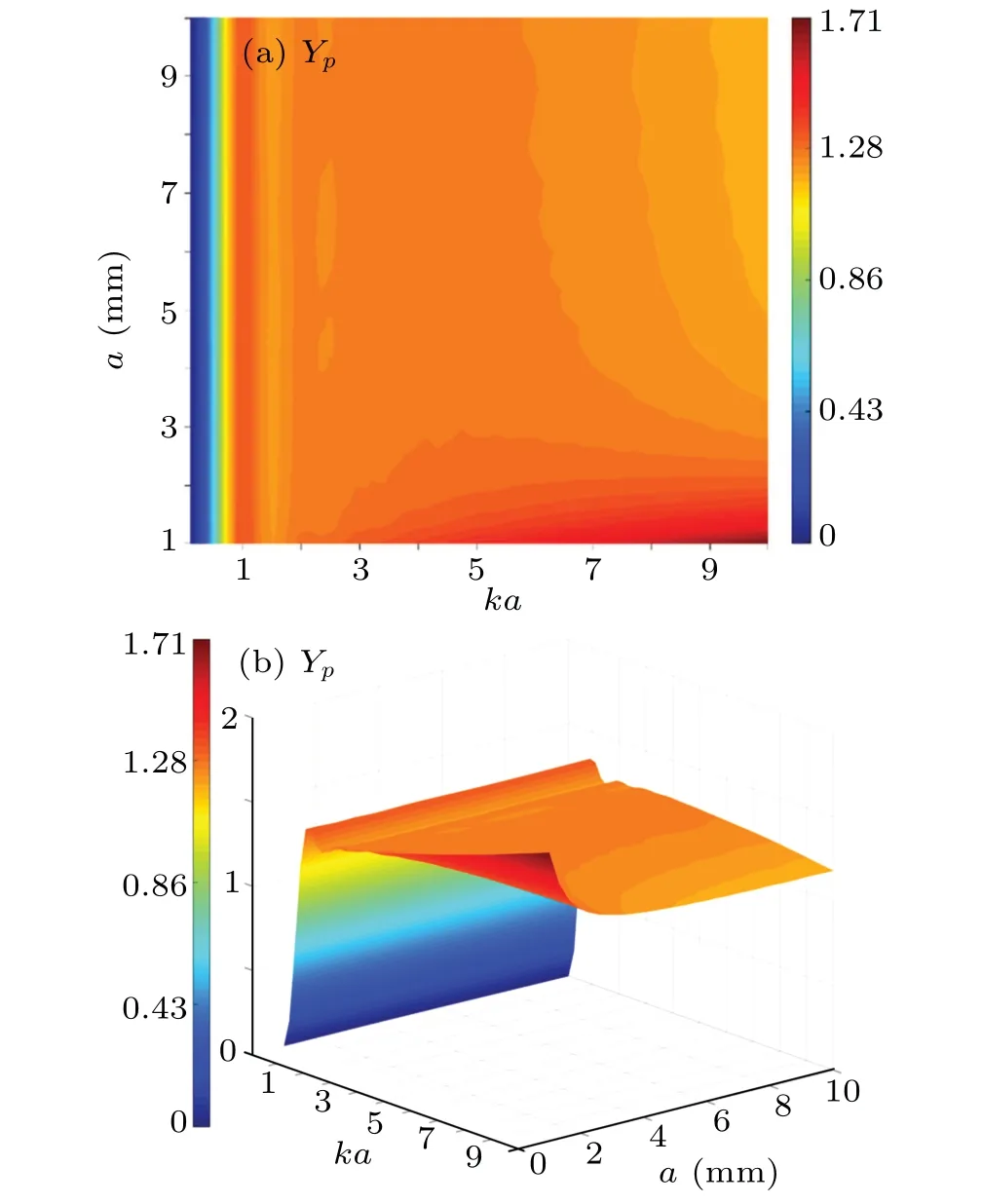
Fig.9. The axial acoustic radiation force function component Yp versus a and ka for a rigid cylindrical in free space exerted by an optical Gaussian beam field. (a) The 2D plots of Yp. (b) The 3D plots of Yp, with ka=10.

Varying the values ofwandka, the simulated results of the axial acoustic radiation force functionsYxandYyare shown in Fig. 10. It is shown thatYxandYyare both constant whenkais lower than 6. However, ifkais larger than 6,YxandYydecrease with increasingw. The results suggest that the axial acoustic radiation force is affected by the ratio ofatoλ. Only when the radius of particle is large enough (the ratio is large enough),YxandYyare sensitive to the variation ofw.

It is particular to note that all of the color bars in these figures are set symmetric about zero to make the positive values red and the negative values blue,which makes it easier for readers to distinguish the positive and negative values.

Fig. 10. The 2D plots of the acoustic radiation force function components versus ka and w for a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The angle α between two rigid boundaries is set as 120°,the incident angle φ is set as 0° and the normalized distance d1 =d2 =2. (a) The acoustic radiation force component in the X direction. (b) The acoustic radiation force component in the Y direction.

Figure 11 plots the axial radiation force functionsYxandYyversus the normalized distancesd1andd2. It is found thatYxandYyvaries periodically along with the change ofd2at a certaind1value. However, the amplitudes of theYxandYypeaks decrease with the increase ofd1when the value ofd1is around from 2 to 5; whend1is more than 5, the amplitudes ofYxandYyare stable. Switchingd1andd2will lead to the analogous results.

The regular patterns verify thatYxandYyare influenced by the standing wave existing between rigid boundaries and the surface of particle. As the distancesd1andd2change,YxandYywill be enhanced or weaken frequently when they meet the conditions of the standing wave. In addition,it shows that the positions of the maximal values are identical whereas the values are opposite.This phenomenon is due to the fact thatYxandYyare two components of the acoustic radiation force. If each one becomes the maximum,the other must be minimal.

It is noteworthy that there exists the negative acoustic radiation force at selectedd1andd2values,where the backscattering of the sphere is suppressed.

All the parameters are kept the same as those in Figs. 11(a) and 11(b) exceptka(ka=1) and the results are shown in Figs.11(c)-11(f). Since the value ofkais smaller in this case,the details of transformation tendency of the acoustic radiation force function in large wavelength are clearer. Considering thatd2ranges from 2 to 7,YxandYyare more sensitive to the variation ofd1and it can be observed that the transformation frequency of acoustic radiation force tends to be higher asd2becomes smaller. Ifkais smaller (ka=0.5), the phenomenon is more obvious as shown in Figs. 11(e) and 11(f).Combined with the conclusionska=3,the increase ofd2does not influence the transformation frequency whend2increases so as to generate the third peak. In addition,negative acoustic radiation force is also found, in that case the backscattering acoustic scattering is suppressed.

Fig.11. The 2D plots of the acoustic radiation force function components versus d1 and d2 for a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The angle α between two rigid boundaries is set as 120°,the incident angle φ is set as 0° and the beam waist w is set as 3. [(a),(c),(d)]The acoustic radiation force component in the X direction. [(b),(d),(f)]The acoustic radiation force component in the Y direction. In(a),(b),(c),(d),(e)and(f),the ka is set as 3,3,1,1,0.5 and 0.5,respectively.

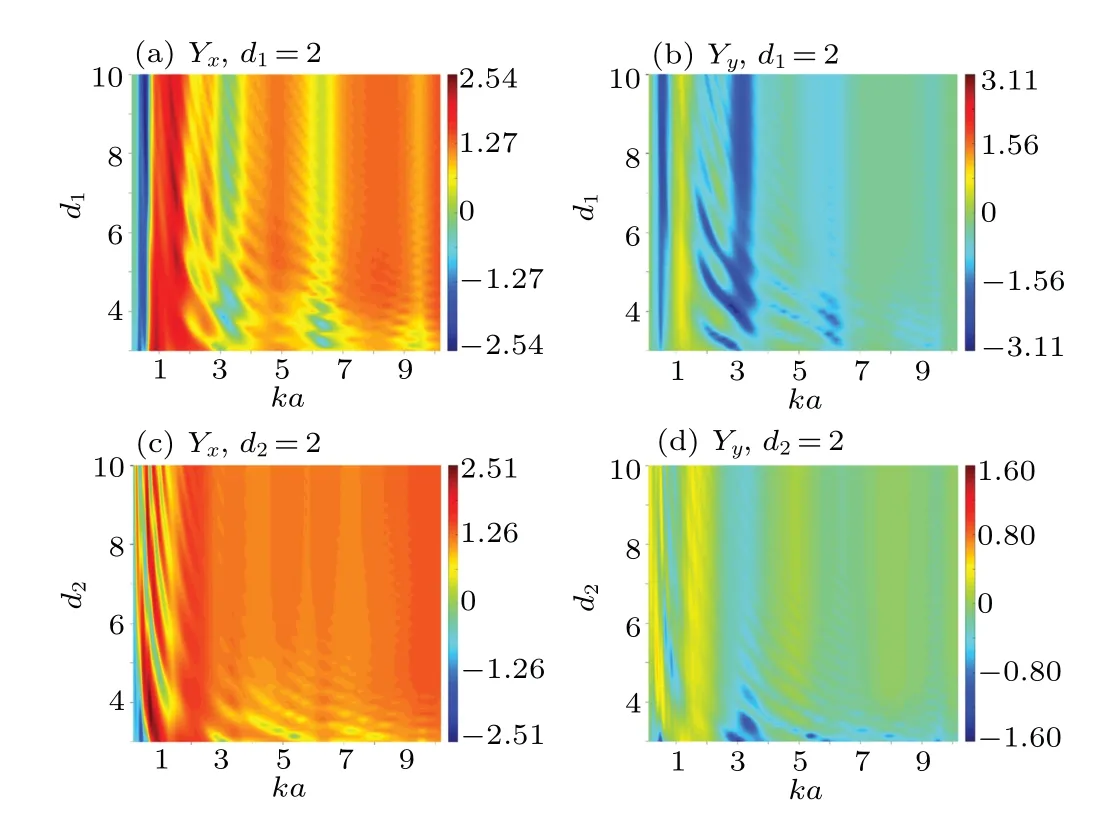
Fig. 12. The 2D plots of the acoustic radiation force function components versus ka and each normalized distances for a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The angle α between two rigid boundaries is set as 120°, the incident angle φ is set as 0°and the normalized radius of beam waist w is set as 3. [(a),(c)]The acoustic radiation force component in the X direction. [(b), (d)]The acoustic radiation force component in the Y direction. [(a), (b)]The d2 is set as 2. [(c),(d)]The d1 is set as 2.

According to the results in Fig.12,the values ofd1andd2are varied independently to figure out the relationship between the normalized distance andka. It is similar to Fig.10,when the normalized wavelength is larger than particle radius(kais small enough),YxandYyare insensitive tod1ord2. However,askaincreases,YxandYyexhibit periodical variations along withd1ord2and there is a positive correlation between the beam frequency andka. All of the above phenomena are also caused by the standing wave. Whenkais fixed, the quantity of peaks will increase with the increase ofd1ord2, and vice versa.

In real applications, the angle between two boundaries and the incident angle are often varied to meet different demands. Figure 13 predicts the 2D plots of the acoustic radiation force function components versuskaandαfor a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The incident wave is set to be in parallel to theXaxis, and the normalized radius of beam waistwis set as 3. Figure 14 shows the corresponding plots for the radiation force functions versuskaandφatα=120°andw=3. The maximal and minimal values of the acoustic radiation force function can be easily observed in the simulated plots.

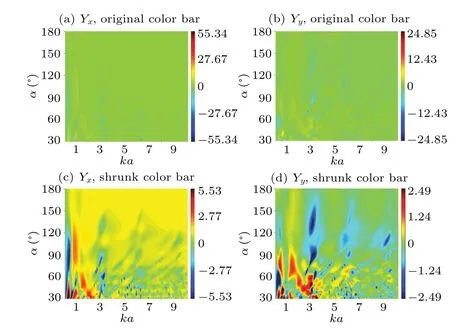
Fig. 13. The 2D plots of the acoustic radiation force function components versus ka and α for a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The incident angle φ is set as 0°,and the normalized radius of beam waist w is set as 3. [(a),(c)]The acoustic radiation force component in the X direction. [(b), (d)] The acoustic radiation force component in the Y direction. In (a) and (b), the color bar is original. In(c)and(d),the color bar is shrunk to one tenth of the original.

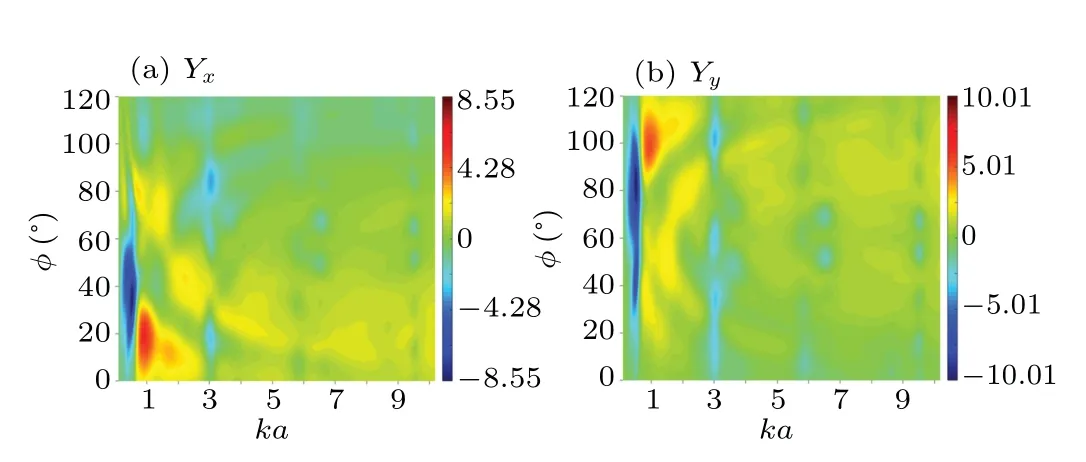
Fig. 14. The 2D plots of the acoustic radiation force function components versus ka and φ for a rigid cylindrical particle near a rigid corner placed in a Gaussian beam field. The angle α between two rigid boundaries is set as 120°, and the normalized distance d1 =d2 =2. (a) The acoustic radiation force component in the X direction. (b)The acoustic radiation force component in the Y direction.

On the basis of the results of the rigid corner case, it is convenient to calculate the acoustic radiation force function on a particle nearby arbitrary boundaries.An example is given here to demonstrate the calculation of the acoustic radiation force function on a rigid cylindrical particle nearby a circular rigid corner,in which the curvature radius of circular corner is set as 2a. The comparison between the numerical models for a right angle rigid corner and a circular rigid corner is shown in Fig.15.

Fig. 15. The numerical models of two types of rigid corners. The angle α between two rigid boundaries is set as 90°, the incident angle φ is set as 0° and the normalized distance d1 =d2 =2. (a)The meshes for the right angle rigid corner model. (b)The meshes for the circular rigid corner model. (c)The total acoustic pressure field Pt for the right angle rigid corner model. (d)The total acoustic pressure field Pt for the circular rigid corner model.

Figure 16 exhibits the 2D plots of the acoustic radiation force function components versuskaandwfor a rigid cylindrical particle near two types of corners placed in a Gaussian beam field. The color bars of Figs. 16(c) and 16(d) are, respectively,adjusted to the same as in Figs. 16(a) and 16(b) to contrast clearly with other figures. The transformation tendencies of the acoustic radiation force function of two types boundaries are basically the same, butYxis weakened andYxis enhanced in the circular rigid corner case due to the reflection of the circular boundary. It is feasible to analyze more complex boundaries by changing the parameters of model.

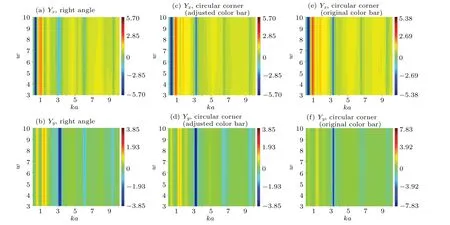
Fig. 16. The 2D plots of the acoustic radiation force function components versus ka and w for a rigid cylindrical particle near two types of rigid corners placed in a Gaussian beam field. The angle α between two rigid boundaries is set as 90°,the incident angle φ is set as 0° and the normalized distance d1=d2=2. (a)The acoustic radiation force component in the Y direction of the right angle rigid corner. (b)The acoustic radiation force component in the Y direction of the right angle rigid corner. [(c),(e)]The acoustic radiation force component in the X direction of the circular rigid corner. [(d),(f)]The acoustic radiation force component in the Y direction of the circular rigid corner.

4. Conclusions

In summary, an FEM numerical model is presented for the acoustic radiation force exerting on a rigid cylindrical particle immersed in fluid near a rigid corner,which is so difficult to figure out by PWSEM because of the complex reflection from boundaries. Compared with PESEM,FEM is more suitable to calculate the acoustic radiation force existed in intricate geometries.

Numerical simulation shows that the amplitude of the acoustic radiation force function has visible changes at smallkadue to ratio ofatoλ. The transformation of the acoustic radiation force depends on the generation of standing wave that the tendency is significantly affected bykaand the distance from the center of cylinder to each boundary. Whenkadecreases, the variation frequency of acoustic radiation force function appears obvious oscillations along with the distance.The positions of the acoustic radiation force function peaks change withka. This study provides a numerical method to calculate the acoustic radiation force on a particle nearby multiple boundaries and is expected to improve and develop the acoustic particle manipulation in practical applications.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11604361 and 11904384), the National Key R&D Program of China (Grant No.2018YFC0114900),and Youth Innovation Promotion Association,Chinese Academy of Sciences(Grant No.2019024).