Decoding the electron dynamics in high-order harmonic generation from asymmetric molecular ions in elliptically polarized laser fields

Cai-Ping Zhang(张彩萍) and Xiang-Yang Miao(苗向阳)

1College of Physics and Information Engineering,Shanxi Normal University,Taiyuan 030031,China

2Key Laboratory of Spectral Measurement and Analysis of Shanxi Province,Shanxi Normal University,Taiyuan 030031,China

Keywords: asymmetric molecular ion,high-order harmonic generation,electron dynamics,elliptically polarized laser field

1. Introduction

High-order harmonic generation (HHG),[1-5]a hot topic in the strong-field physics, has wide applications such as generating the attosecond pulse,[6,7]detecting the ultrafast electron motion,[8]imaging the molecular orbital,[9]reconstructing the band structures,[10,11]and exploring structural strain.[12,13]The physical mechanism of the gas HHG has been well explained via a three-step model:[14]ionizationacceleration-recombination, indicating the dominant role of the ground-state dynamics. In fact, the harmonic generation also records the excited-state dynamics.[15,16]For the symmetric molecular ions, it can be encoded in both the lower-order[15]and the higher-order harmonics.[16]The former is attributed to the two-center interference, while the latter is ascribed to the electron localization. With dynamical symmetry breaking, the even harmonics from the symmetric molecular ions can manifest the excited-state dynamics in both linearly and elliptically polarized laser fields.[17,18]For the asymmetric molecular ions, the electron dynamics in the harmonic generation process is more complex due to the existence of the permanent dipole.[19-22]Based on the Born-Oppenheimer approximation (BOA), the four-step model (excitation-ionization-acceleration-recombination) has been proposed to interpret the related underlying mechanism in linearly polarized laser fields.[23,24]Additionally,the lowerorder resonant peak has been ascribed to the electron transition between the ground state and the excited state. It indicates the important role of the excited state in harmonic emission.[25]Moreover, by establishing the multichannel recombination model based on the non-BOA,our group has discussed the electron dynamics of the ground and the excited states in detail.[26-28]

As mentioned above, both the ground state and the excited state can contribute to the harmonic emission in strong laser fields. Thus the harmonics from different electronic states will strongly couple with each other. It is known that an elliptically polarized laser field affects the harmonic emission along the minor axis and the major axis of the polarization ellipse.[29]Then, the elliptically polarized laser pulse can be probably used to explore the complex harmonics from asymmetric molecular ions. To understand the related electron dynamics,we select the simple single-electron HeH2+as the model to study the harmonic generation process in elliptically polarized laser fields. Via solving the two-dimensional(2D) time-dependent Schr¨odinger equation (TDSE), the harmonic intensity is periodically ellipticity-dependent.This phenomenon records the important role of the excited-state dynamics in harmonic emission. With the time-frequency distribution,the populations of different electronic states and the laser-dressed double-well model, the underlying electron dynamics is tracked in detail. Moreover,we propose an efficient way to decode the harmonics from the ground state and the excited state by combining the elliptically polarized laser field and the static electric field. Atomic units(a.u.) are used in this paper unless otherwise stated.

2. Theoretical method

The harmonic emission from HeH2+has been investigated by solving the 2D TDSE.Providing the molecular axis along with thexaxis, in the dipole approximation and the length gauge,the 2D TDSE can be written as[30-32]

Here,Z1= 0.81 andZ2= 1.62 are the effective charges of H and He, respectively;R1=Z2R/(Z1+Z2) andR2=Z1R/(Z1+Z2),respectively;a=b=0.05 is selected to avoid the Coulomb singularity.[21]WithR=4 a.u., the eigenfunctions and energy eigenvalues of different electronic states can be obtained via the diagonalization of the field-free Hamiltonian. The energy of the ground state is-2.25 a.u. forR=4 a.u.[33]With higher ionization potential for the ground state,stronger laser intensity can be used to emit higher harmonic energy. It can benefit the observation of the interesting phenomena. Thus the ground state is selected as the initial state,which has been widely used in theoretical studies for strongfield-induced dynamics of asymmetric molecules.[21,24]

The strong elliptical laser field is expressed as

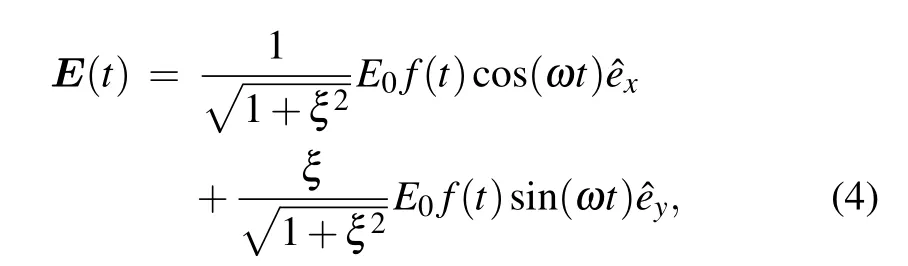
whereξis the ellipticity, ˆexand ˆeyare the unit vectors alongxandyaxes, respectively (i.e., the major axis and the minor axis of the polarization ellipse);f(t)is a trapezoidal envelope function with total duration of ten optical cycles (o.c.) and three cycles ramp on, four cycles are constant and three cycles ramp off. Here, 1 o.c.=2.0 fs corresponds to the wavelength of 600 nm. Moreover, with cos1/8mask function, the time-dependent wave function is achieved by the second-order split-operator method.[16,34]The converged numerical parameters are as follows: the grid ranges inxandydirections are from-200 a.u. to 200 a.u. with Δx=Δy=0.4 a.u., respectively. The time step is Δt=0.05 a.u.

3. Results and discussion

3.1. Electron dynamics of harmonic emission from HeH2+in elliptically polarized laser fields

Due to the laser polarization along with the molecular axis, the electrons in the ground state can be pumped to the first excited state in a strong linearly polarized laser field.[26,27]Then,both the ground state and the first excited state will contribute to the harmonic generation. Different from the linearly polarized laser field, an elliptical laser pulse affects the harmonic emission in two directions, i.e., along with the major(x) and minor (y) axes of the polarization ellipse. So much richer electron dynamics can be obtained from the harmonic emission in elliptically polarized laser fields. Figure 1 demonstrates the time-frequency maps of HeH2+in elliptically polarized laser fields expressed as Eq. (4) with different values of ellipticityξ. The corresponding wavelength is 600 nm and the laser peak intensity isI= 3.0×1015W/cm2. Forξ= 0.1, the harmonic intensity aroundtr= (n+0.25) o.c.is stronger than that aroundtr= (n+0.75) o.c. However,with the increase ofξfrom 0.2 to 0.3, the harmonic intensity aroundtr=(n+0.25) o.c. tends to be weaker than that aroundtr=(n+0.75) o.c. as illustrated in Figs. 1(b)-1(d).Heretrrepresents the recombination moment. Additionally,with similar periodical character of harmonic intensity as that in Fig. 1(a), the related results for 0≤ξ ＜0.1 are not displayed here. How about the electron dynamics in strong elliptically polarized laser fields? The detail discussion will be provided in the following part.

In the strong elliptically polarized laser field,the electricfield strength alongyaxis will be enhanced with the increase ofξ.Moreover,the second excited state will be excited for the perpendicular orientation.As shown in Figs.2(a)and 2(b),the population of the second excited state is obviously enhanced fromξ=0.1 toξ=0.25, especially from (n+0.5) o.c. to(n+1) o.c. (i.e., the negative laser field alongydirection).In this case,the ground state is dressed up,and then the electrons in the ground state can be easily pumped to the second excited state. To get across the physical origin of the periodical harmonic intensity in elliptically polarized laser fields as mentioned above,the probabilities ofP0(t)=1-|〈0|φ(t)〉|2(red solid line),P1(t)=1-∑1n=0|〈n|φ(t)〉|2(gray solid line)andPion(t)=1-∑9n=0|〈n|φ(t)〉|2(black solid line)are presented forξ=0.1 andξ=0.25 in Figs.2(c)and 2(d),respectively. The difference betweenP0(t) andPion(t) can reflect the possible contribution of the ionization from excited states.Moreover, the areas of shadow regionScan reflect the effective ionization process occurring in the falling edge of electric field. Here the harmonic emissions aroundtr=4.25 o.c.(ti=3.5 o.c.) andtr=4.75 o.c. (ti=4.0 o.c.) are selected as examples;tirepresents the ionization moment. Clearly,S1in Fig. 2(c) is nearly equal toS2in Fig. 2(d). Namely, the similar ionization probabilities from the excited states. Comparisons of Figs.2(c)and 2(d)demonstrate that the ionization from the ground state aroundti=3.5 o.c. decreases with the increase ofξas shown by pink dashed lines. Thus, the related harmonic emission aroundtr=4.25 o.c.becomes weaker forξ= 0.25. Furthermore, with smaller ionization potential,much more electrons of the second excited state can contribute to the harmonic emission aroundtr=4.75 o.c. Then,the harmonic intensity aroundtr=4.75 o.c. is stronger than that aroundtr=4.25 o.c. forξ=0.25. Additionally, this phenomenon tends to be much more obvious for largerξas displayed in Fig. 1(d). Generally speaking, the excited-state dynamics makes a great effect on the harmonic emission from asymmetric molecular ions in elliptically polarized laser fields.

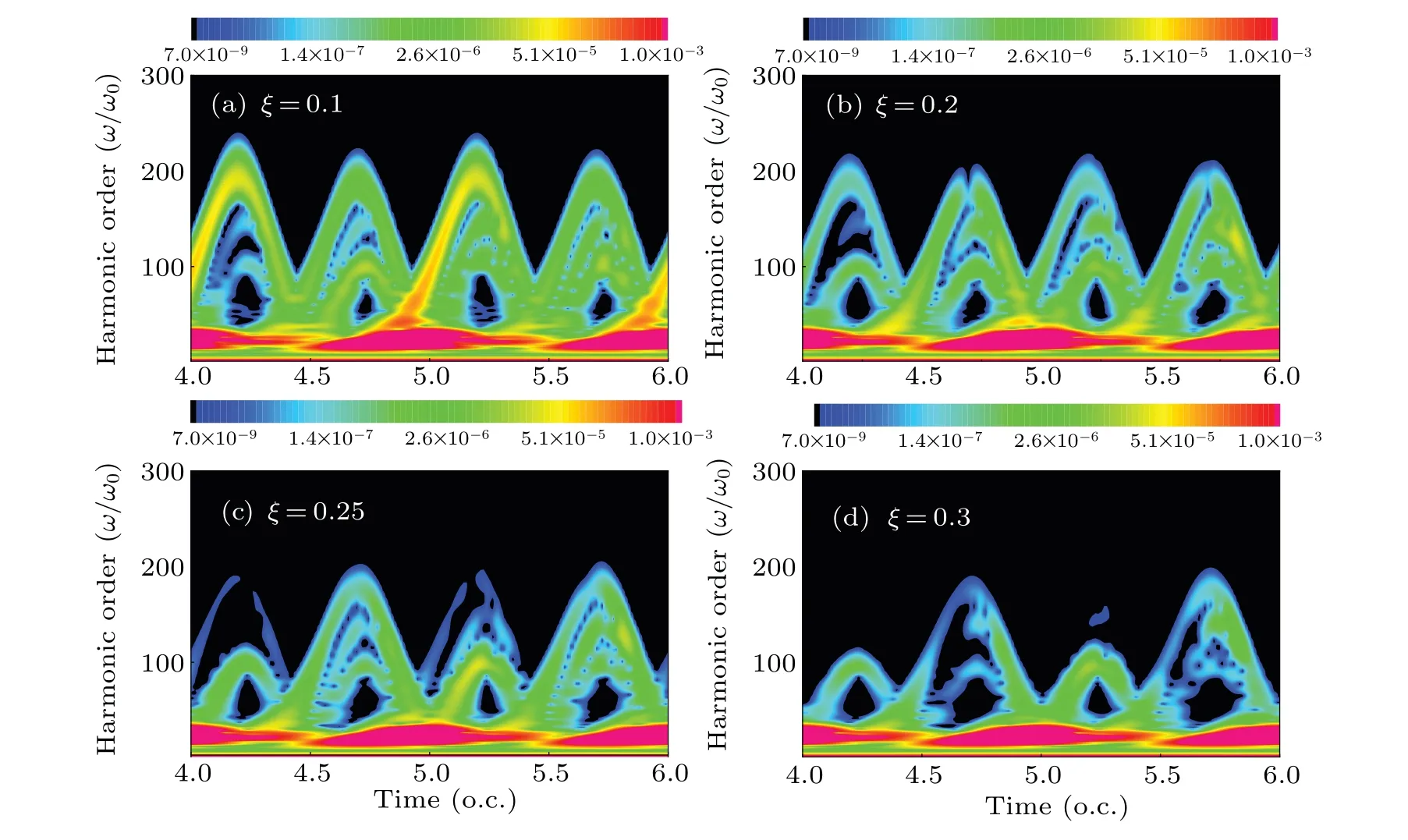
Fig. 1. Time-frequency maps of HeH2+ in elliptically polarized laser fields with the wavelength of 600 nm and laser peak intensity of I =3.0×1015 W/cm2 for different values of ellipticity ξ: (a)ξ =0.1,(b)ξ =0.2,(c)ξ =0.25,and(d)ξ =0.3.

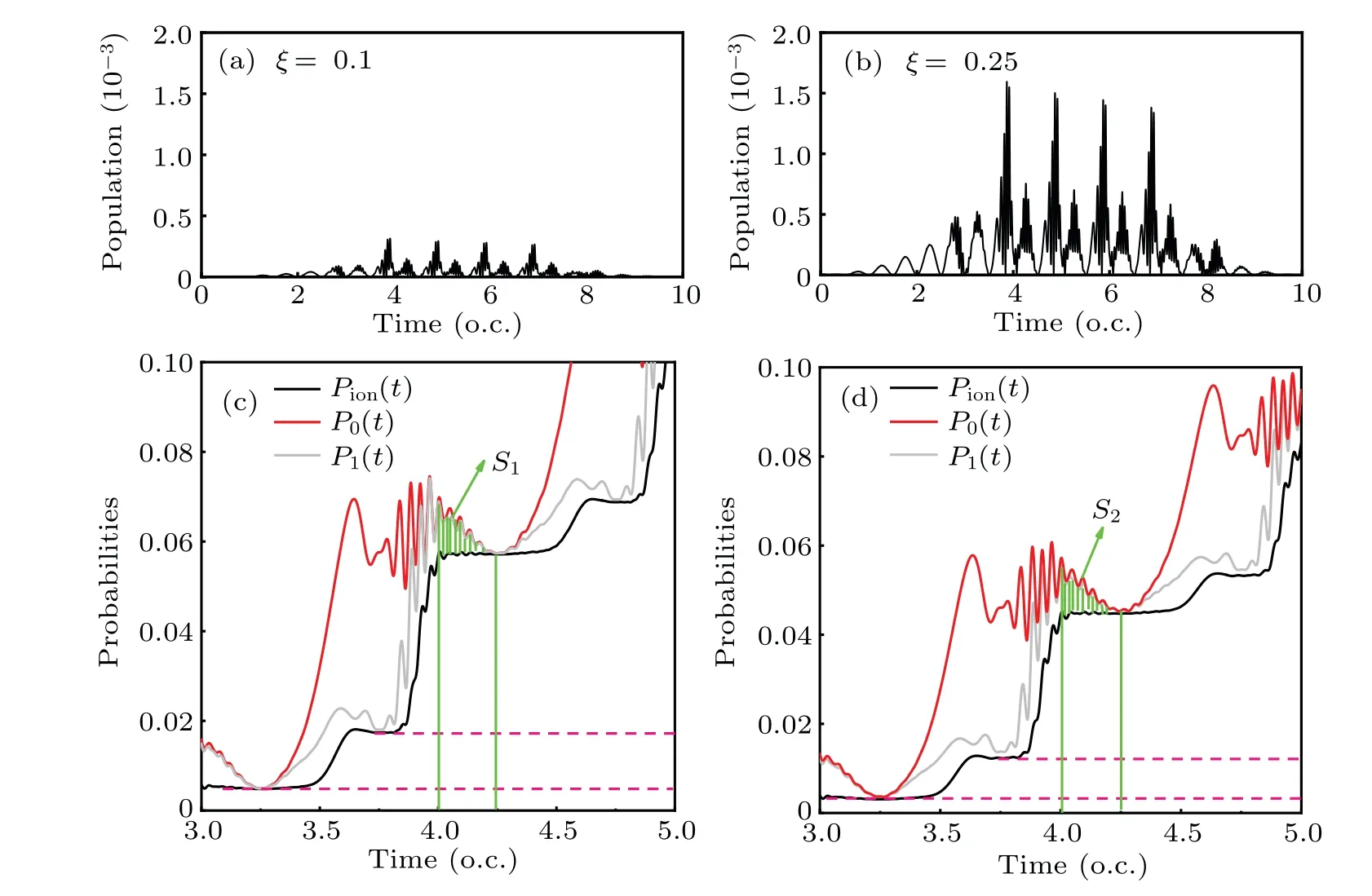
Fig. 2. Populations of the second excited state for different ξ: (a) ξ =0.1 and (b) ξ =0.25, respectively. (c) and (d) The probabilities of P0(t)=1-|〈0|φ(t)〉|2(red solid line),P1(t)=1-∑1n=0|〈n|φ(t)〉|2(gray solid line)and Pion(t)=1-∑9n=0|〈n|φ(t)〉|2(black solid line)for the cases of ξ =0.1 and ξ =0.25,respectively.

To further reveal the underlying mechanism,the physical image of the harmonic generation from HeH2+is established.In Fig.3,the purple,red and magenta dots represent the electrons in the ground state(|0〉), the first excited state(|1〉)and the second excited state (|2〉), respectively. The electron motion can be described as follows: forEx ＜0 andξ= 0 in Fig. 3(a) (i.e., in the linearly polarized laser field), the electron in the ground state can be transited to the excited states,especially the first excited state (process 1, black solid line).Moreover,the stronger the laser intensity is,the more the electrons are pumped to the first excited state. Under the interaction of the peak intensity aroundt=(n+0.5) o.c. alongxdirection, the electron in the dressed-up ground state can tunnel out the inner barrier (process 2, red solid line) and propagates in the external laser field (process 3, blue solid line). When the laser field reverses its direction, the ionized electrons can return back to recombine with the ground state(progress 4,green solid line)because the electrons mainly locate in the ground state and few can survive in the first excited state.[21,22]Additionally, forEx ＞0 andξ=0 in Fig. 3(b),the potential well of the first excited state is dressed up while that of the ground state is dressed down. Thus the electrons in the first excited state can also contribute to the harmonic emission via ionization(red solid line)-acceleration(blue solid line)-recombination (green solid line) process. The excitedground state channel still dominates the harmonic generation.Forξ ＞0, enhanced amplitude of electric field inydirection will induce complex electron motion in elliptically polarized laser fields. As shown in Fig. 3(c), forEy ＜0, the electrons in the ground state can be pumped to the second excited state(process 1＇, black dashed line). For smaller value ofξ, the electrons pumped to the second excited state are few,and then the harmonic generation process is mainly affected byEx. In this case, the harmonic intensity as shown in Fig. 1(a) will exhibit similar periodical characters with that in a linearly polarized laser field. However, with the increase ofξ, the electrons of the dressed-up ground state can be much more easily pumped to the second excited state in negative field along withydirection. Then the electrons in the ground state are reduced, resulting in the suppressed harmonic emission from the ground-state channel via ionization(process 2＇,red dashed line)-acceleration(process 3＇,blue dashed line)-recombination(process 4＇, green dashed line). However, forEy ＞0, more electrons can be ionized from the second excited state, and the harmonic emission process from the second excited state shown in Fig. 3(d) will be enhanced. Additionally, with few electrons,the electron dynamics of the higher excited states is not discussed in this section.

Fig. 3. The sketch of electron motion in strong laser field. The black solid(dashed) line, red solid (dashed) line, the blue solid (dashed) line and the green solid(dashed)line represent the excitation,ionization,acceleration and recombination processes for ξ =0(ξ ＞0),respectively. The purple dot,red dot and magenta dot represent the electrons of the ground state|0〉, the first excited state|1〉and the second excited state|2〉,respectively.

As discussed above, the elliptically polarized laser field can exert great effects on the electron transition process.Moreover, for smallerξ= 0, it mainly affects the electron transition between the ground state and the first excited state,while the larger one mainly affects the electron transition between the ground state and the second excited state.In general,the excited states can play an important role in the harmonic emission from HeH2+.

3.2. Decoding the electron dynamics in different electronic states

When asymmetric molecular ions are irradiated by strong laser pulses, both the ground state and the excited state contribute to the harmonic generation. In this case, the electron dynamics becomes more complicated and the harmonics from different electronic states are difficult to be chosen. As we know that the static electric field has been widely used to adjust the fundamental laser field to manipulate gas HHG.[25,35]In this section, we will resolve the harmonic emission from different electronic states via combining an elliptically polarized laser field and a static electric field expressed in the following. The laser intensity alongycan be adjusted by the static electric field

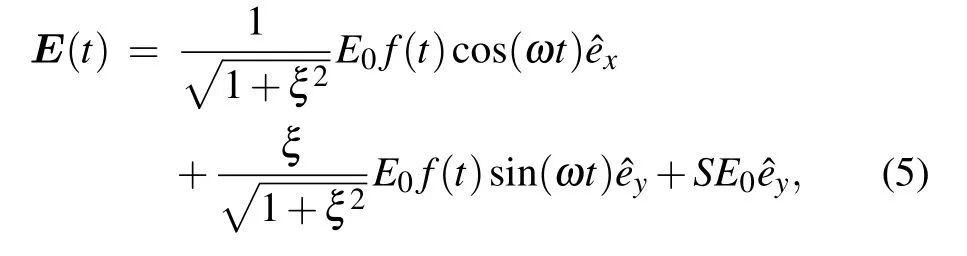
where parameterSis used to adjust the amplitude of the static electric field. Withξ=0.25 andI=3.0×1015W/cm2, the combined electric fields inydirection are plotted for different values ofSin Fig.4(a):S=0(gray solid line),S=0.16(blue dashed line) andS=-0.2 (red dotted line), respectively. The related time-frequency distributions in the combined laser fields are displayed in Figs.4(b)and 4(c). Clearly,withS=-0.2(the strength of the static electric field is about 2.98×108V/cm), the negative peak intensity alongyaxis is increased while the positive peak intensity is decreased as shown by the red dotted line. Based on the physical model described in Fig.3,on the one hand,with stronger negative peak intensity,the population of the excited states will be enhanced,which results in the strong ionization from the excited states.On the other hand, the ionized electrons from the ground state are difficult to return back under the interaction of the weaker positive field compared with the case ofS=0. Consequently,the harmonics are dominated by the electrons in the excited state as displayed in Fig.4(b). It is easy to understand that, when the positive static electric field withS=0.16 (the strength of the static electric field is about 2.39×108V/cm)is superposed to the elliptically polarized laser field alongyaxis,the harmonic emission is mainly controlled by the ground state as demonstrated in Fig.4(c). In conclusion,the complex harmonic emission from different electronic states can be selected by the combination of an elliptically polarized laser field and a strong static electric field. Moreover, the strong static electric fields mentioned above can be generated by low-frequency sources,such as free-electron lasers.[36]

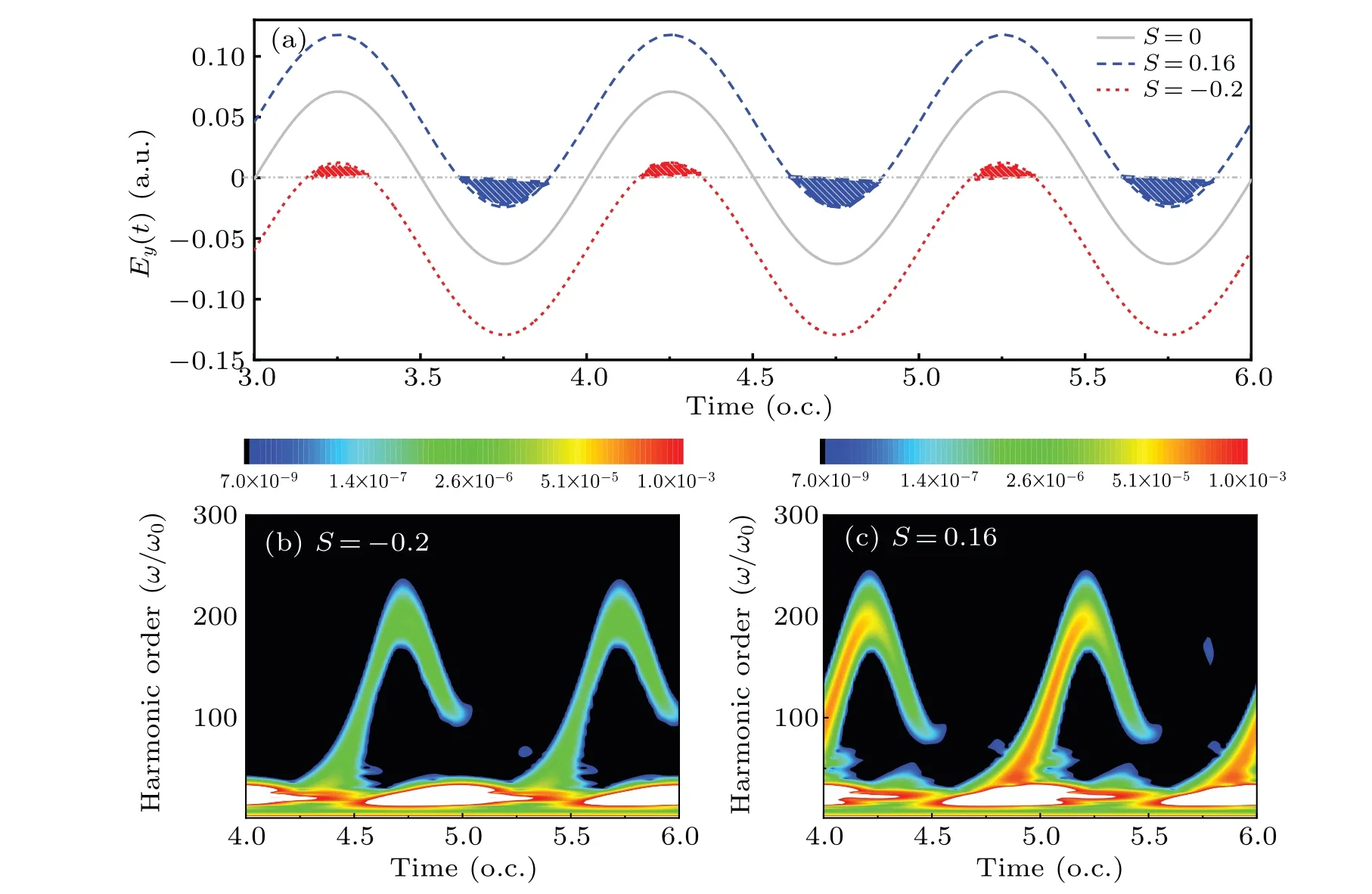
Fig.4. (a)The sketch of the combined electric fields along y axis with ξ =0.25 and I=3.0×1015 W/cm2 for different static parameters:S=0(gray solid line), S=-0.2 (red dotted line) and S=0.16 (blue dashed line), respectively; (b) and (c) time-frequency maps in the combined laser fields with S=-0.2 and S=0.16,respectively.

4. Conclusion

In summary, we have investigated the electron dynamics in the harmonic generation from asymmetric molecular ions in elliptically polarized laser fields by numerically solving the two-dimensional time-dependent Schr¨odinger equation based on the Born-Oppenheimer approximation. The harmonic intensity exhibits an ellipticity-dependent periodical character,which is closely related to the electron transition from the ground state to the higher excited states. In addition, the harmonic emission from different electronic states can be resolved by the combination of an elliptically polarized laser field and a static electric field.For the case ofξ=0.25 andI=3.0×1015W/cm2, the harmonic emission mainly originates from the ground state around(n+0.25)o.c. with the strength of the positive static electric field of 2.39×108V/cm,while it is mainly from the excited state around(n+0.75)o.c.with the strength of the negative static electric field of 2.98×108V/cm.Here, the strong static electric field can be achieved via low frequency laser field. In general,the electron dynamics of the ground state and the excited state can be detected by harmonic emission despite of the strong coupling of electronic states in strong laser fields.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11974229, 11404204, and 11947002) and the Scientific and Technological Innovation Program of Higher Education Institutions in Shanxi, China(Grant No.2021L255).