Quantum and quasiclassical dynamics of C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction:Coriolis coupling effects and stereodynamics

Dong Liu(刘栋) Lulu Zhang(张路路) Juan Zhao(赵娟) Qin Zhang(张芹)Yuzhi Song(宋玉志) and Qingtian Meng(孟庆田)

1School of Science,Shandong Jiaotong University,Jinan 250357,China

2School of Physics and Electronics,Shandong Normal University,Jinan 250358,China

Keywords: quantum dynamics,quasiclassical trajectory method,C+H2

1. Introduction

The reactions containing neutral carbon atom play a significant part in the astrophysics of interstellar medium and combustion chemistry.[1-3]As the simplest carbon-containing reaction, C+H2is important in atmospheric and hydrocarbon combustion. So far, a lot experimentalists[4-9]and theoreticians[10-24]focus on this reaction,its reverse reaction,and potential energy surface(PES).

The reactions of C(1D)+H2(1Σ+g) based on the singlet states of methylene molecule have been extensively explored,but the investigations about the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction based on the triplet electronic ground state of CH2(˜X3A＇＇) are limited. In order to study C(1D)+H2(1Σ+g)reactions, Bussery-Honvault team respectively constructed the full dimensional and adiabatic PESs of CH2for the first 11A＇(BHL PES)[20]and second 11A＇＇(BJHL PES)[21]singlet states using 1748 and 4644ab initiopoints. Then Ba˜nares and co-authors[25]rebuilt the 11A＇state PES based on the same 1748ab initiopoints employing the reproducing kernel Hilbert space (RKHS) interpolation method. Their dynamic results are consistent with those obtained on the BHL PES.Based on the BHL PES,Luet al.[26]studied the scalar and vector properties of H(2S)+CH(2Π)→C(1D)+H2(1Σ+g) reaction applying the quasiclassical trajectory(QCT)and time-dependent wave-packet(TDWP)methods. Lin and Guo[27,28]calculated the probabilities, integral cross sections (ICSs), and rate coefficients using the Chebyshev wave packet method based on RKHS PES.Soon after,another 11A＇PES was constructed by Joseph and Varandas[11]employing double many-body expansion(DMBE)formula and about 2500ab initiopoints. They further investigated CD/CH branching ratio and isotope effect on the C(1D)+H2(1Σ+g) reaction with QCT method. Different from the previous 11A＇PES, the PES (called ZMB-a PES) fitted by Zhang and co-workers[29]can accurately describe the regions around conical intersections (CIs) and of van der Waals (vdW) interactions. Due to the differences of the PESs in the regions around the CIs and vdW complexes,Wuet al.[30]found that at low collision energies, the values of ICS are much bigger than the previous QCT. Afterwards,based on ZMB-a PES,a lot of dynamic calculations have been done.[31-35]

Concerning the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction, its dynamical calculation needs a full-dimensional PES of CH2(˜X3A＇＇). In 1993, Hardinget al.[17]fitted an accurate three-dimensional (3D) PES of triplet electronic state of CH2by employing multireference configuration interaction (MRCI) method. This PES can well describe the conical intersections includingC2vgeometries between the3B1and3A2states and linear geometries between the3Πand3Σ-states. Then the rate constant of H(2S)+CH(2Π)→C(3P)+H2(1Σ+g)reaction was calculated in their work.Based on this PES,Harreveltet al.[36]explicated minor quantum effects in the CH(2Π)+H(2S)→C(3P)+H2(1Σ+g)reaction by testing calculated reaction probabilities, which illustrates the QCT method can supply realistic estimates of ICSs and the rate constants. Lately, the dynamics of H(2S)+CH(2Π)→C(3P)+H2(1Σ+g)/H(2S)+CH(2Π) reactions were explored in depth by Gamalloet al.[23]with quantum mechanical(QM)method. In their work, by analysis of the correlation diagram of the CH2electronic states ˜X3A＇＇, ˜A3A＇＇, ˜a1A＇, and ˜b1A＇＇, and by test of the Renner-Teller and spin-orbit nonadiabatic calculations on ˜X3A＇＇, ˜a1A＇, and ˜b1A＇＇, they found that the H(2S)+CH(2Π) reactions occur essentially on the uncoupled ˜X3A＇＇ground surface. Recently, our team also fitted the CH2(˜X3A＇＇)PES,[24]and based on it the probabilities,ICSs,and rate coefficients were calculated,which are in good agreement with other theoretical results. Subsequently,the reaction mechanism, vibrational excitation, and isotope effects on the H(2S)+CH(2Π) reaction were analyzed in detail by our group[37]using the QCT method.

The present work is to explore the dynamics of the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π) reaction based on recent CH2(˜X3A＇＇)PES[24]according to QM and QCT methods.The schematic representation of the reaction energy profile of the PES is depicted in Fig.1(a). This panel reflected the title reaction with an endothermic of 1.109 eV, and existence of a deep well with 3.467 eV.

The rest of this paper is organized as follows: In Section 2,we briefly describe the method including QM and QCT calculations. In Section 3, we discuss the Coriolis coupling effects on the title reaction and analyze its stereodynamics.Finally,the conclusions are summarized in Section 4.

2. Methods

2.1. QM calculations

The QM TDWP method is employed to numerically solve the time-dependent nuclear Schr¨odinger equation using the second-order split-operator scheme, referred to the relevant articles.[38-43]In calculations,the Hamiltonian is expressed in the reactant Jacobi coordinates. Convergence tests are carried out with the total reaction probability forJ=0 and the optimal numerical parameters are as follows.In the reactant Jacobi coordinates, theRcoordinate is set in the range of 0.1 a.u.-30.0 a.u. and the diatomic vibrational coordinate is set to be 0.5 a.u.-25.0 a.u. The number of translational and vibrational basis functions is 300 and 210, respectively. The total propagation time is 6×104a.u. with the time step being 10 a.u.All calculations are performed using both centrifugal sudden(CS) approximation and coupled-channel (CC, including the Coriolis coupling)withK=5 used in the CC calculations.

2.2. QCT calculations

Figure 1(b) describes the angle relationship between the initial relative velocity and the final relative velocity vectors in the center-of-mass reference frame, which can be well understood as product rotational polarizations.[44-48]kandk＇respectively denote the relative velocity vectors of reactant and product inx-zplane,and they are connected by the angleθt.j＇is the product rotational angular momentum,andθrandφrare the dihedral and the azimuthal angles of it respectively. The distribution functionP(θr)describes thek-j＇correlation withj＇·k=cosθr,expanded in a series of Legendre polynomials,

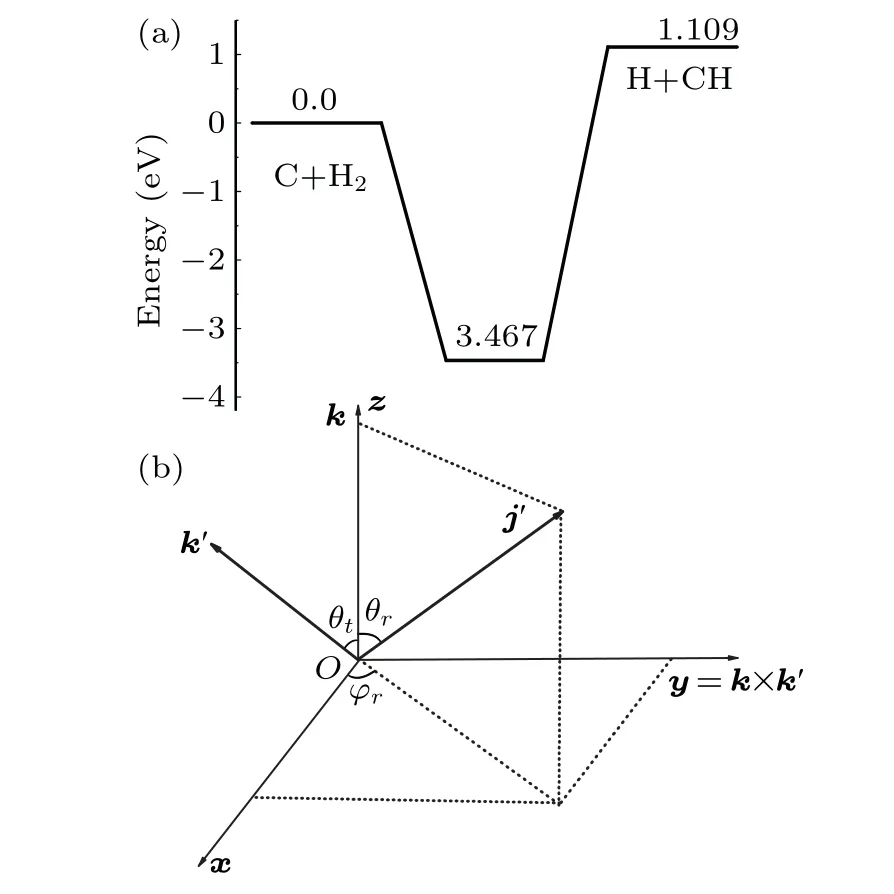
Fig. 1. (a) Schematic diagram of the PES for C(3P)+H2(1Σ+g ) →H(2S)+CH(2Π)reaction.(b)The xyz center-of-mass coordinate system used to describe the k-k＇-j＇ correlations.

3. Results and discussion

3.1. Probability,integral cross sections,and rate constant

The reaction probabilities are calculated as a function of collision energy by employing QCT and QM methods for total angular momentumJ=0 displayed in Fig.2(a). It is easily found that the reaction probability obtained by QM method presents a strong oscillation in the range of 1.0 eV-2.0 eV.It is mainly because of the property of the CH2(˜X3A＇＇)PES that has a deep potential well with the complex-forming mechanism. Overall, the reaction probability increases with the increase of collision energy, which is originated from that the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction is an endothermic reaction. It should be noted that in the range of 1.0 eV-1.1 eV,the collision energy is not big enough to cross the barrier of the system(greater than 1.1 eV),but the reaction probability is still not zero, which can be explained by the quantum tunneling effect. It is noteworthy that the inferiority of QCT reaction probabilities compared to the QM results enlarges with the increase of collision energy,from which we can conclude that the tunneling and zero-point energy effects cannot be ignored for the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction.

Figure 2(b)shows the ICSs in the collision energy range of 1.0 eV to 2.0 eV. The ICSs first increases rapidly and then moderately with a small fluctuation in the same collision range. Compared with the probability in the upper panel,the oscillation structures in the QM ICS curves are obviously weakened, caused by theJ-average effect washing out the structures. Unlike the QM results, the ICSs calculated by QCT method show a least fluctuation and a most smoothness among the three methods. It can be indicated that the quantum effects caused resonances originated from the PES with the deeper potential well. We note that the ICSs calculated by QM method including the Coriolis coupling are always higher than the corresponding ICSs of CS in the entire collision energy range, and as the collision energy increases, the gap between the CS and CC ICSs is more obvious,indicating that the Coriolis coupling should not be ignored. Moreover, the QCT results are moderate among the three methods for collision energy bigger than 1.25 eV and become smallest for lower energy range. This significant discrepancies between QCT and CC methods are on account of the title reaction involving double H atoms causing obvious quantum effects. According to the above discussion, we can conclude that the QCT method is not appropriate for studying the ICSs and rate constants of the title reaction, which could provide theoretical support for the future study of this system.

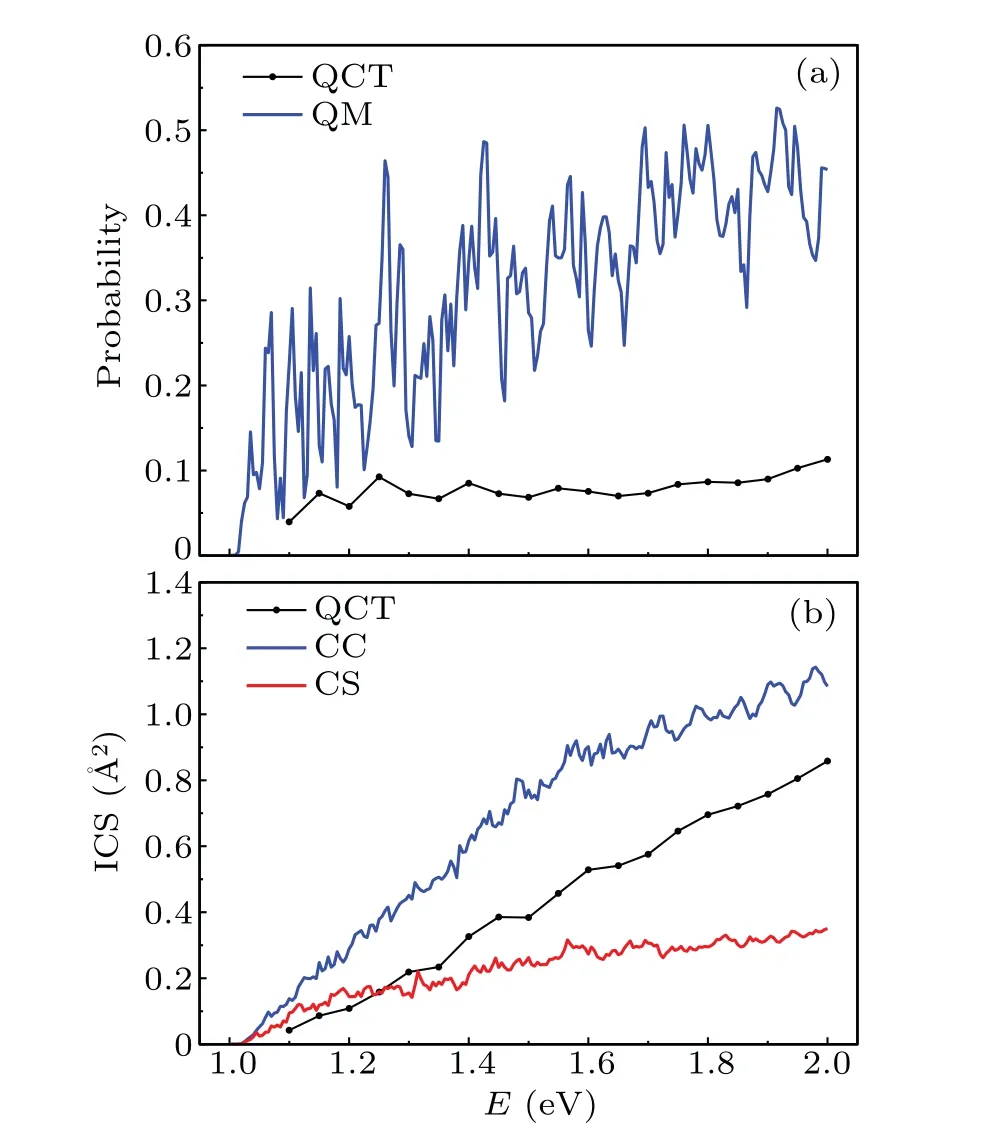
Fig. 2. The calculated reaction probability and ICS as a function of collision energy by employing QCT and QM methods.

Figure 3 indicates the CS and CC reaction probabilities for C(3P)+H2(1Σ+g)→H(2S)+CH(2Π)reaction forJ=5,10, 20, 30, 40, and 50 to explore the role of Coriolis coupling in this reaction with a deep well. Many sharp resonance peaks of probability appear because of the deep well on the CH2(˜X3A＇＇) PES. Both the CS and CC methods results increase with the increasing energy 1.0 eV-2.0 eV but decline with increasingJ. The reactional thresholds arise and become larger asJrises. This indicates that the centrifugal barrier impedes the combination of C and H atoms. ForJ=5, the CS probabilities are larger than CC probabilities, while forJbeing bigger than 5, the probabilities are reversed and the dispersion between the two methods is more remarkable for largerJ. It is owing to the reactant molecule,H2,confined by just includingK0=0 quantum states in the CS approximation,which increases the opportunity for the sudden collision with C atom and then forms the product more easily with fewer resonances,resulting in overestimation of the reaction probability. WithJincreasing to a certain extent, much more partial waves contribute to the breaking of the collision complex through Coriolis coupling and thus facilitating the formation of the CH molecule. Consequently, whenJbecomes larger,the differences between the CS and CC probabilities are observed to be more and more remarkable, and in more details,theJ-dependent behavior is observed that the CC probabilities tend to increase with increasingJ. The above analysis shows that the Coriolis coupling effect is large and cannot be ignored.

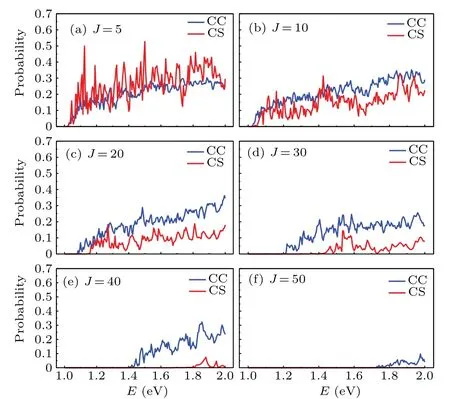
Fig.3. Comparison between the CC and CS probabilities in the collision energy range of 1.0 eV to 2.0 eV for the total angular momentum(a)J=5,(b)J=10,(c)J=20,(d)J=30,(e)J=40,and(f)J=50.

In the temperature range from 1000 K to 2000 K,the rate constant of the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π) reaction is given in Fig. 4, obtained from the two different QM calculations. In calculations,the electronic population

is introduced. The two different QM calculations suggest the rate constant of CC calculations is stably higher than the corresponding CS method. Both the CC and CS results show the similar decline trend with the temperature reduced and the CC rate constant reduces among 10-16cm3/s to 10-13cm3/s from 1000 K to 2000 K.For the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π) reaction, it is obvious that the influence of Coriolis coupling on the title reaction is significant,and neglecting the Coriolis coupling for the title reaction is inappropriate.

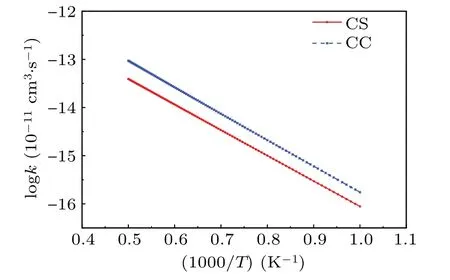
Fig.4. Comparison between the CC and CS rate coefficients.

3.2. Stereodynamics

Because the trend of ICS calculated by QCT method is consistent with that by QM method, we can use QCT method to explore the stereodynamics information of the title reaction. Figure 5 shows thek-k＇-j＇correlation and the scattering direction of the product molecule CH for the C(3P)+H2(1Σ+g)→H(2S)+CH(2Π) reaction according to the collision energy ranging from 1.0 eV to 2.0 eV described by the PDDCSs. Because the PDDCS00explains thek-k＇correlation and is just proportional to the differential cross section (DCS), it is easily found in panel (a) that the products are scattered both forward and backward. The larger the collision energy, the stronger the backward scattering. The reason for these results may be the PES has a deep potential well, and the indirect reaction mechanism dominates in the lower collision energy. And the complex in the indirect reaction has a long lifetime, so a symmetric product distribution can be easily formed. As the collision energy increases,the direct reaction mechanism begins to work. The shortened life of the complex leads to the partial forward or backward scattering, which gives the asymmetric distribution of DCS with the scattering angle. The panel (b) displays the PDDCS20of(2π/σ)(dσ20/dωt),which is not only related toθt,but also a function of〈(3cos2θr-1)〉. When the value of〈(3cos2θr-1)〉is negative,j＇is strongly aligned perpendicular tokdirection. The behavior of PDDCS20is opposite to that of PDDCS00, and it is negative for both backwards and forwards scattered products,indicating thatj＇is preferentially aligned along the direction perpendicular tok.

The PDDCSs withq/= 0 are shown in panels (c) and(d). Because thek-k＇scattering plane is uncertain at the extreme of the scattering angle, so the values of PDDCSs are zero atθ=0 andθ=π. Otherwise, the PDDCSs provide information aboutφr. And the values of PDDCSs are nonzero between 0 andπ, this indicates that theP(θr,φr) distribution is anisotropic for scattering products. The PDDCSs of (2π/σ)(dσ22+/dωt) and (2π/σ)(dσ21-/dωt) are respectively in connection with the〈(sin2θrcos2φr)〉and〈(sin2θrcosφr)〉. When the PDDCS22+is negative, product alignment is along theyaxis,otherwise,the product alignment is along thexaxis. And when the PDDCS21-is negative,the product alignment is along the direction of the vectorx+z,while the PDDCS21-is positive means the product alignment along the direction of vectorx-z. As shown in Fig.5(c),the PDDCS21-distribution is negative in most scattering angles,especially atθt=140°andEc=1.2 eV-1.6 eV, showing a clear product alignment along theyaxis. While in panel (d),the value of the PDDCS21-is clearly negative atθt=160°andEc=1.7 eV-1.9 eV, so the product alignment is along the direction of the vectorx+z.

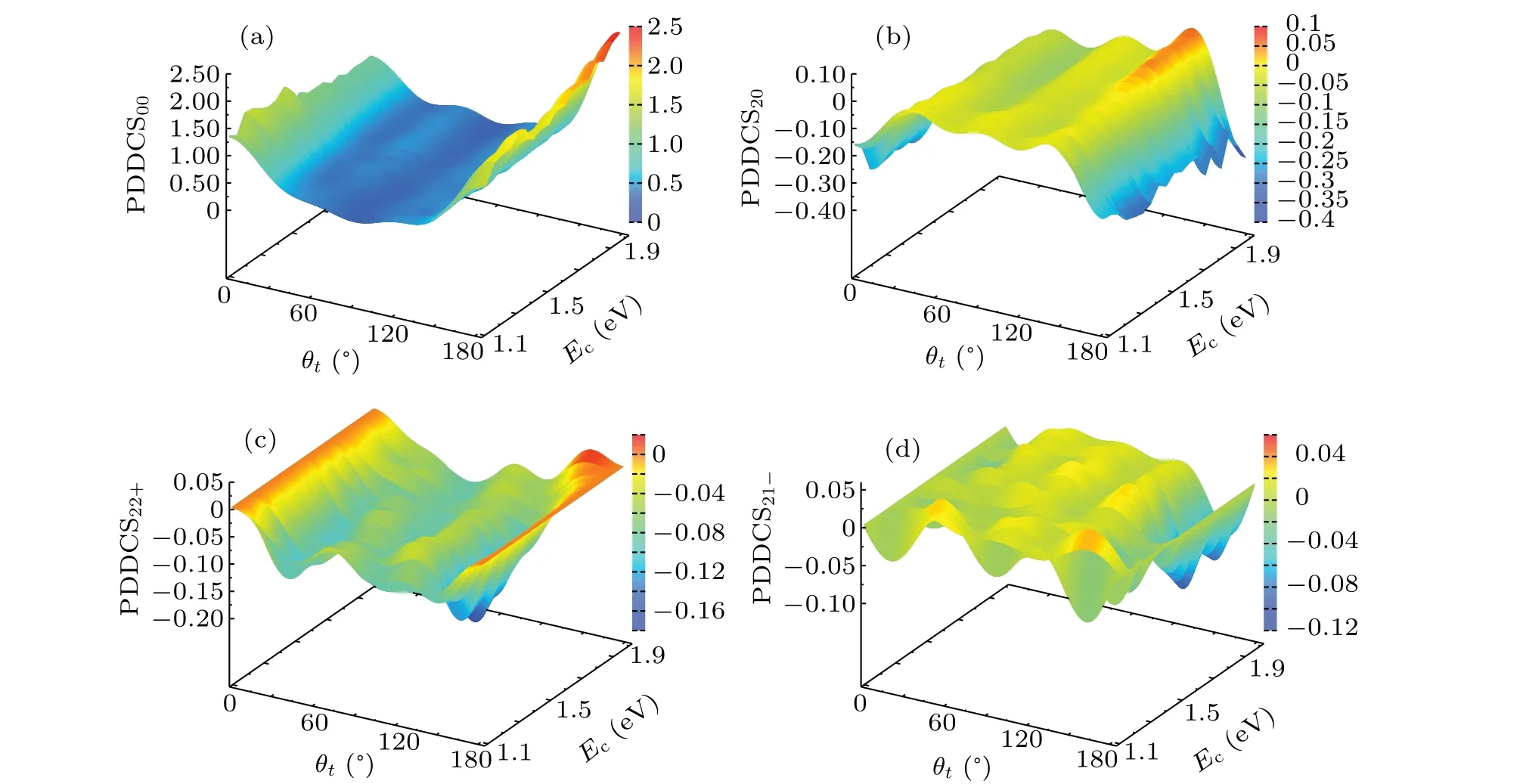
Fig.5. The differential cross sections as functions of both the scattering angle θt over the range of 0°-180° and the collision energy over the range of 1.0 eV-2.0 eV.

TheP(θr)distribution over the range of 0°-180°and energy covering the range of 1.1 eV-2.0 eV is described in Fig.6.The distribution are symmetric aboutθr=90°,and a 90°peak is obvious, which shows the rotational angular momentum alignment vertical to the reactant relative velocity and the remarkable polarization. Overall, there are a slight increase ofP(θr) with increasing collision energy ranging from 1.0 eV-2.0 eV. The collision energy influences theP(θr) distribution positively and moderately.1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, and 2.0 eV. In this figure we can find that theP(φr)is asymmetric with respect to thekk＇scattering plane,and the peak atφr=90°is higher than atφr=270°. The result indicates that the rotational angular momentum vectorj＇of the product molecule is not only aligned,but also strongly oriented along the positiveyaxis.

Fig.6. The angular distribution of P(θr)replacing k-j＇ correlation as functions of both angles of 0°-180° and the collision energy over the range of 1.0 eV-2.0 eV.

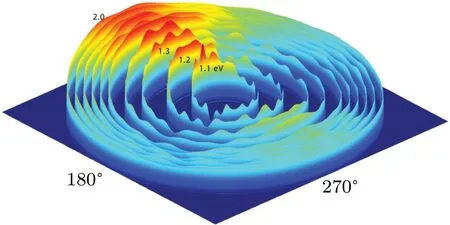
Fig.7. The dihedral angle distributions of P(φr)describing the k-k＇-j＇correlation as functions of the dihedral angle φr at ten collision energies of 1.1,1.2,1.3,1.4,1.5,1.6,1.7,1.8,1.9,and 2.0 eV.

Figure 7 shows the dihedral angle distributions ofP(φr)describing thek-k＇-j＇correlation at collision energies of 1.1,

4. Conclusions

We have performed QM and QCT calculations for the C+H2→H+CH reaction on the lowest triplet state CH2(˜X3A＇＇)PES. The discrepancies between QM probabilities and QCT probabilities show that the tunneling and zero-point energy effects can not to be ignored for the reaction. The ICSs,probabilities and rate constants calculated by QM method including the Coriolis coupling are always higher than the corresponding that of CS in the entire collision energy range, indicating values the Coriolis coupling should not be ignored. The calculated normalized PDDCS shows that the products are scattered both forward and backward,and the larger the collision energy, the stronger the backward scattering. The analysis ofP(θr) andP(φr) distributions tells that thej＇of the rotational angular momentum of product molecule is not only aligned vertical to the reactant relative velocity, but also strongly oriented along the positiveyaxis. The present work can provide theoretical support for choosing which method to study the system in the future.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 11904394 and 12004216) and the Natural Science Foundation of Shandong Province,China(Grant No.ZR2020QA064).