Thermodynamically consistent model for diblock copolymer melts coupled with an electric field

Xiaowen Shen(沈晓文) and Qi Wang(王奇)

1School of Physical and Mathematical Sciences,Nanjing Tech University,Nanjing 211816,China

2Beijing Computational Science Research Center,Beijing 100193,China

3Department of Mathematics,University of South Carolina,Columbia,SC 29208,USA

Keywords: thermodynamical consistency,diblock copolymer melts,electric field,phase field model

1. Intro duction

The block copolymer comprises of two or more homopolymer subunits linked by covalent bonds. Copolymer melts consist of copolymers in liquid phase in high temperatures while copolymer solutions are mixtures of copolymers and solvents. In the diblock copolymer melt, the copolymer consists of polymerAand polymerBexclusively in two distinctive blocks. In the copolymer solution,either water or another homopolymer can serve as the additional phase,known as the solvent. Diblock copolymer systems can self-assemble into various ordered mesoscopic structures as the result of polymer-polymer and/or polymer-solvent interactions, which are often exploited in materials science and engineering, in particular,in nanotechnologies.[1-5]

The self-consistent field approach and associated numerical simulation have been proven to be effective means to investigate coarsening dynamics in copolymer systems. The seminal work of Ohta and Kawasaki[6]laid the foundation of phase field models for diblock copolymer systems. Ohtaet al.also considered models for mixtures of diblock copolymers and a third immiscible phase.[7]Choksi and Ren[8,9]analyzed the models with rigorous mathematical techniques in minimization of free energy functionals. Coupling an external electric field or magnetic field to copolymer systems is one of the effective ways to manipulate and fabricate various nanostructured materials in materials’ self-assembly involving copolymers and the nanoparticle phase.[10,11]Interesting mesoscopic morphologies can be obtained by quenching in melts or applying evaporation in solutions. The electric or magnetic field assisted self-assembly is a cutting-edge research in materials science and engineering today.

When the electric field is coupled to a diblock copolymer system, dipoles are induced so that the electric field is fully coupled to dynamics of the copolymer system.The existing phase field models for this system,however,have adopted an effective or simplified coupling term to include the electric field effect, resulting in models that do not have proper free energies not mention corresponding energy dissipation laws.[12-26]Because of this, we declare the resulting simplified models thermodynamically inconsistent. These thermodynamically inconsistent phase field models coupled with the electric field are based on two original papers,[27,28]where significant simplifications were carried out. The thermodynamical inconsistency may prevent one from accurately predicting transient morphology of the diblock copolymer system when coupled with the electric field. Note that thermodynamical consistency here refers to the positive entropy production principle or equivalently the free energy dissipation principle in isothermal cases in nonequilibrium thermodynamics expressed either as the generalized Onsager principle or as the second law of thermodynamics.[29-33]It is an important principle to follow when one devises quantitative models for any material systems and accompanying numerical algorithms for these models.

The rest of this paper is organized as follows. The mathematical model and accompanying second order numerical algorithms for diblock copolymer melts coupled with an electric field is developed in Section 2. In Section 3,the numerical investigations are carried out,where we compare relaxation dynamics of the thermodynamically consistent model developed with that of the existing thermodynamically inconsistent one.The conclusion is summarized in Section 4.

2. Thermodynamically consistent model and numerical algorithms

2.1. Diblock copolymer melts coupled with an electric field

We cannot find any proper free energy functional for this model that yields a negative energy dissipation rate. Hence,we regard this model as thermodynamically inconsistent!

2.2. Second order linear numerical algorithms

We present a 2n order energy dissipation rate preserving numerical algorithm to solve the thermodynamically consistent model numerically. We also use a numerical algorithm of the same order to solve the thermodynamically inconsistent model.

In order to mitigate potential numerical singularity, we regularize the logarithmic potential in the model by aC2piecewise function.[35]Specifically,for 0＜σ ≪1,we modified the bulk free energy as follows:

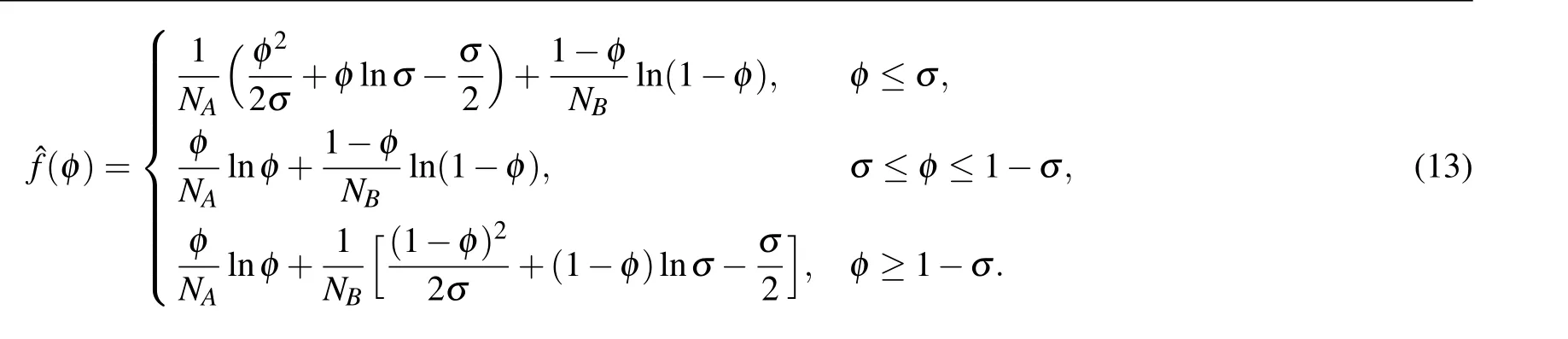
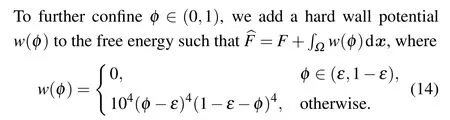
We useσ=ε=0.01 in the following numerical simulation. However,for simplicity,we retain all original mathematical symbols in the presentation of algorithms.

2.2.1. Notations used in discretization

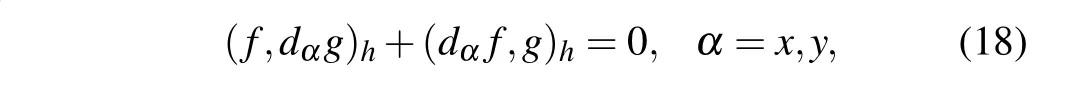
whenfandgsatisfy proper boundary integrals with vanishing boundary conditions.

On the cell-centered grid,the boundary conditions we use in this study can be easily implemented by using the scheme and the discrete summation-by-parts formulae.

2.2.2. Linear implicit Crank-Nicolson schemes

Applying the linear implicit Crank-Nicolson discretization in time, we obtain a second order EQ algorithm for the E-BCP model(7)as follows.

Alorithm 1 E-BCP Assumingφn-1,φnare known, we computeφn+1by

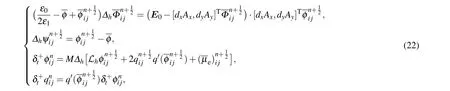
where 1≤i ≤Nxand 1≤j ≤Ny.

This numerical scheme is thermodynamically consistent at the discrete level.

For completeness, we present a second order EQ algorithm for the S-E-BCP model(12)as follows.

Algorithm 2 S-E-BCP Assumingφn-1,φnare known,we computeφn+1through

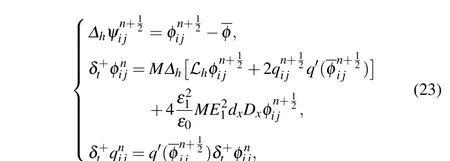
where 1≤i ≤Nxand 1≤j ≤Ny.

This numerical scheme is not thermodynamically consistent at the discrete level.

3. Numerical results

We numerically compare differences of transient dynamics between E-BCP model (7) and S-E-BCP model (12). We fixΩ=[0,1]×[0,1], Δt=10-5,hx=hy=1/128 to conduct the numerical investigation. We setNA= 3,NB= 7,χ=6,γ=1.8×10-3,M=4×10-3,ε0=1,E0=[10,0]Tandε1= 0.2, 0.3 respectively. The initial conditions areφ0=φ0A=0.3+10-3×rand(x,y) andφ0B=1-φ0A, where rand(x,y)∈(-1,1)is a random number generator that follows the uniform distribution. Some phase portraits and induced electric fields at selected time slots are plotted in Figs. 1-4 and the total free energy of the E-BCP model is depicted in Fig.5.

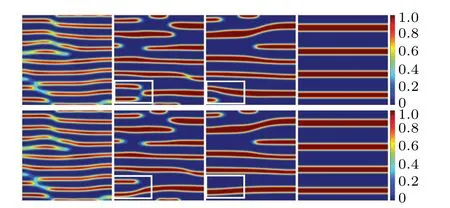
Fig. 1. Transient dynamics of phase separation and coarsening when ε1=0.2(S-E-BCP and E-BCP model in the 1st,2nd row respectively).Color map of phase φA at t=0.2,0.6,1,20 respectively.The rectangles highlight the difference.

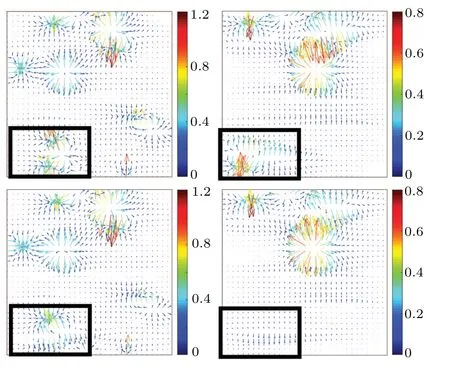
Fig.2. Induced electric field ∇Φ at t=0.6, 1 when ε1=0.2(S-E-BCP and E-BCP model in the 1st,2nd row respectively). The rectangles highlight the difference.

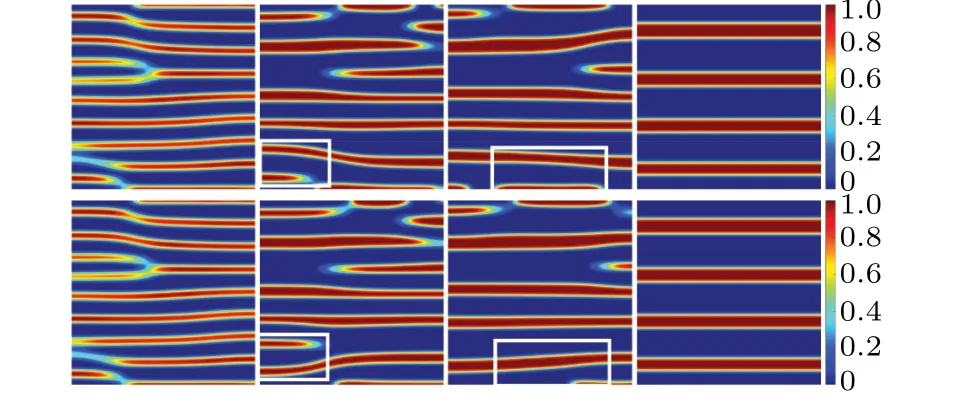
Fig. 3. Transient dynamics of phase separation and coarsening when ε1 =0.3 (S-E-BCP and E-BCP model in the 1st, 2nd row respectively). Color map of phase φA at t=0.2,0.6,1,20 respectively. The rectangles highlight the difference.

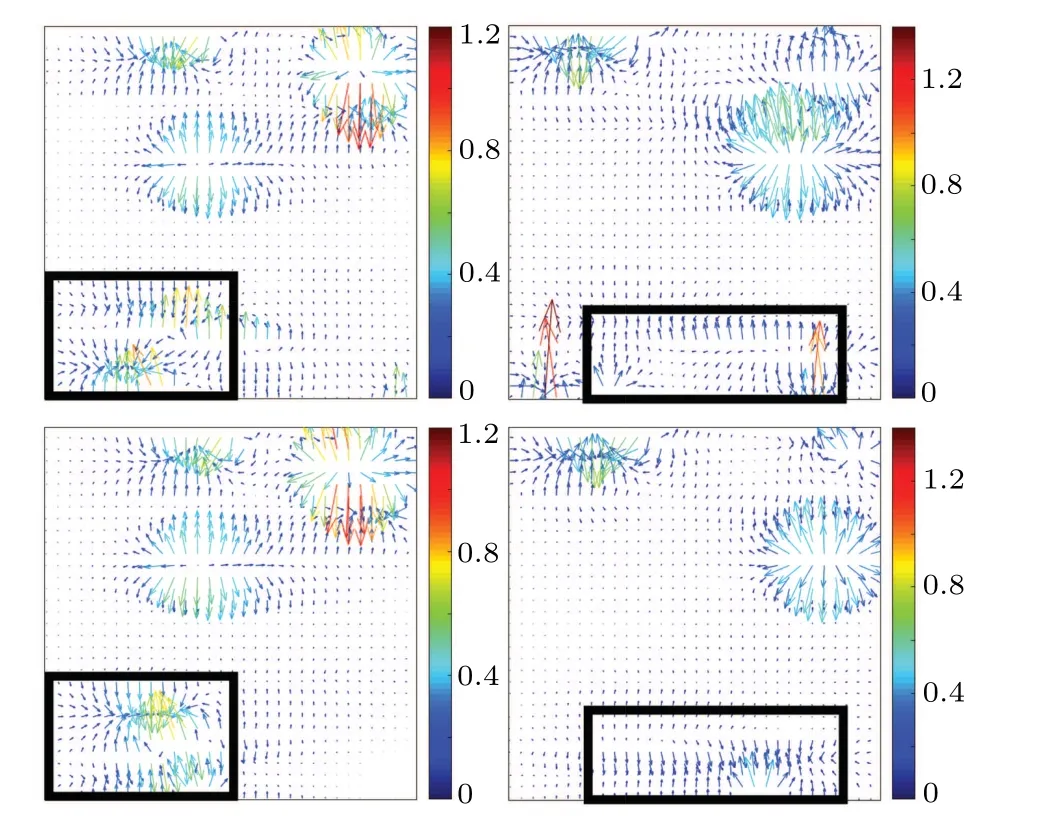
Fig.4. Induced electric field ∇Φ at t=0.6,1 when ε1=0.3(S-E-BCP and E-BCP model in the 1st, 2nd row respectively). The rectangles highlight the difference.

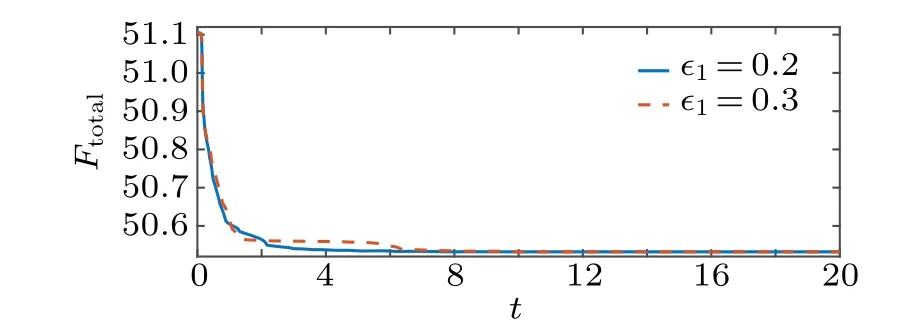
Fig. 5. Total free energy evolution in t ∈[0,20] of E-BCP model at 2 different values of ε1.

When an electric field is coupled to copolymer melts,lamellae normally emerge in time. During transient from an irregular initial phase morphology to the lamellar pattern,branches or bridges are formed momentarily and annihilated eventually by the electric field. This is a process of defect removal in diblock copolymers assisted by external field in material processing,where one refers to the branches as defects.Under the influence of the electric field,structures coarsen to form stripes as well as defects in transient.Defects move along the direction of the electric field and disappear at the boundary of the domain driven by the electric field. The morphology of final structures forms a lamellar pattern with stripes along the direction of the electric field. For different parameter valuesε1=0.2 and 0.3,which parameterize material’s dielectric responses to the electric field,we compute solutions of the two models with the same initial conditions up to when they reach steady states att=20. The two models generate somewhat different induced electric potentials at the sameε1,leading to different transient structures in Figs.1 and 3,respectively. For anyε1, similar patterns emerge at the beginningt=0.2 and similar steady states emerge att=20 between the two models,while transient dynamics are somewhat different(highlighted by rectangle marked areas). The total free energy curves of the thermodynamically consistent model(7)settle down to the steady state with time in Fig.5.

4. Conclusion

In this paper, we derive a thermodynamically consistent phase field model for diblock copolymer melts coupled with the electric field,following fundamental principles of electrodynamics and the generalized Onsager principle. The resulting model respects an energy dissipation law for the total free energy. We then numerically compare the thermodynamically consistent model with an inconsistent one previously used to highlight their differences and thereby to emphasize the importance of thermodynamical consistency. The upshot of this study is that transient dynamics of thermodynamically consistent and inconsistent models can be quite different in morphological details, which can be significant in annealing for copolymer melts and therefore should not be ignored.

Acknowledgements

Xiaowen Shen’s research is partially supported by the National Natural Science Foundation of China (Grant Nos. 11971051 and U1930402). Qi Wang’s research is partially supported by National Science Foundation grants(award DMS-1815921, 1954532 and OIA-1655740) and a GEAR award from SC EPSCoR/IDeA Program.