Effect of carbon nanotubes addition on thermoelectric properties of Ca3Co4O9 ceramics
2022-04-12YaNanLi李亚男PingWu吴平ShiPingZhang张师平YiLiPei裴艺丽JinGuangYang杨金光SenChen陈森andLiWang王立
Ya-Nan Li(李亚男) Ping Wu(吴平) Shi-Ping Zhang(张师平) Yi-Li Pei(裴艺丽)Jin-Guang Yang(杨金光) Sen Chen(陈森) and Li Wang(王立)
1Beijing Key Laboratory for MagnetoPhotoelectrical Composite and Interface Science,School of Mathematics and Physics,University of Science and Technology Beijing,Beijing 100083,China
2School of Energy and Environmental Engineering,University of Science and Technology Beijing,Beijing 100083,China
Keywords: Ca3Co4O9,carbon nanotubes,thermal conductivity,thermoelectric properties
1. Introduction
With the increasingly serious energy shortage and environmental pollution,people need to find green energy and energy conversion methods. Thermoelectric materials can realize the direct conversion of thermal energy and electric energy based on Seebeck effect and Peltier effect, and they have attracted much attention in recent years.[1]The conversion efficiency of thermoelectric materials depends on the figure of meritZT=σS2T/k, whereσis the electrical conductivity,Sis the Seebeck coefficient,Tis the absolute temperature,andκis the thermal conductivity.[2]It can be observed from the above formula that high-efficiency thermoelectric conversion requires high electrical conductivity and Seebeck coefficient,as well as low thermal conductivity,which is quite challenging. The optimization of one parameter of thermal conductivity or electrical conductivity usually causes the reduction of the other parameter. In recent years, compared with intermetallic thermoelectric compounds, such as Bi2Te3,[3]PbTe,[4]etc.,thermoelectric oxide material Ca3Co4O9(abbreviated as CCO) has attracted extensive attention because of its good stability, convenient preparation, green environmental protection and low cost.[5]At present, theZTvalue of polycrystalline Ca3Co4O9still cannot meet the requirements of practical application, which limits its commercial application.
Ca3Co4O9has monoclinic structure, and the chemical formula is[Ca2CoO]b1[CoO2]b2.This represents a monoclinic mismatched sandwich like structure,and a calcium salt disordered layer is mixed between CdI2type CoO2layers,extending along thec-axis. The two layers share the same lattice parameters:a=4.8270(5),c=10.8300(2),β=98.1360(1).The unit cell mismatch changes along theb-axis. The lattice parameterbvalues of Ca2CoO3and CoO2layers areb1=4.5615(2) °A andb2=2.8173(1) °A,respectively,which are usually expressed as[CaCoO][CoO2]1.61.[6]The mismatch and weak connection between Ca2CoO and CoO2layers enhance phonon scattering, reduce thermal conductivity, and lead to significant anisotropy.[7]Due to its unique staggered structure,in order to improve the thermoelectric performance of Ca3Co4O9, the traditional method is to adjust the carrier concentration by doping ions at the Ca position[8-12]or Co position,[13-16]so as to affect the electric transport and phonon scattering. Another strategy is to add nano materials into Ca3Co4O9as the second phase. Theoretically,an appropriate number of composite nanoparticles can enhance the connectivity between grains and grain growth,improving the electrical conductivity. Due to the energy filtration effect, it may help to improve the Seebeck coefficient of the material. Simultaneously, the phonon scattering center is increased, thereby reducing the thermal conductivity. In recent years, the addition of nanoparticle materials to Ca3Co4O9, such as SiC,[17]Bi2O3,[18]NaF,[19]B4C,[20]Ag nanoparticles,[21]etc., has been used to improve the thermoelectric properties of materials. Carbon nanotube (CNT) is a low dimensional material with high conductivity and light weight. Adding carbon nanotubes to reduce the weight of materials for the application of weight sensitive thermoelectric materials is very competitive, for example, microelectronic devices, sensors,etc. Ceramic nano powders are widely used as nano dispersions of thermoelectric nanocomposites because of their low thermal conductivity, but the nanocomposites prepared from these nano dispersions show serious conductivity degradation.In contrast, carbon nanotubes are excellent nano dispersions of thermoelectric nanocomposites because CNTs have high conductivity, and their dispersion in the thermoelectric matrix will not deteriorate the conductivity to the extent caused by ceramic nano powder. Yeoet al.[22]added 0.12% CNTs to (Bi0.2Sb0.8)2Te3, the thermal conductivity of the composite was significantly lower than that of the matrix, which increased theZTvalue by 34%. Kimet al.[23]found that the thermal conductivity decreased significantly by compounding Bi0.5Sb1.5Te3with porous carbon nanomaterials. Theoretically, although carbon nanotubes have high thermal conductivity,the interface between carbon nanotubes and matrix can increase the phonon scattering at the interface and reduce the thermal conductivity, which is expected to improve theZTvalue of the material. Tanget al.previously studied the effect of carbon nanotubes addition on the thermoelectric properties of Ca3Co4O9at low temperature.[24]The thermoelectric properties of carbon nanotubes doped at room temperature and higher temperature have not been studied.
In this work,Ca3Co4O9/xwt.%CNTs(x=0,3,5,7,10)composite thermoelectric materials were prepared by sol-gel method. The effects of adding carbon nanotubes on the electrical properties and thermal conductivity of Ca3Co4O9were systematically investigated.
2. Experimental details
Ca3Co4O9powder samples were prepared by sol-gel method. Weigh the precursor raw materials Ca(NO3)2·4H2O and CO (NO3)2·6H2O at a certain stoichiometric ratio, dissolve the raw materials in deionized water and mix evenly,add a certain amount of citric acid, heat and stir continuously at 352 K until sol is formed. The sol was dried at 393 K for 12 h to obtain the precursor. The precursor was fully ground and sintered at constant temperature of 1073 K for 12 h after selfpropagating treatment.After sintering,the powder sample was evenly mixed with carbon nanotubes(CNTs;0 wt.%,3 wt.%,5 wt.%,7 wt.%,10 wt.%)with a certain mass ratio,and then pressed under the pressure of 30 MPa. Crystallographic structure analysis was performed by Rigaku D/max2500 X diffractometer with CuKαray (λ=1.54056 °A) (40 kV, 200 mA),step size 0.01°,conventional 2θof 10°-60°. The phase composition of the sample was analyzed by angle range diffraction spectrum. The microstructure of the samples was observed by field emission scanning electron microscopy (FESEM,Zeiss supra55). The Seebeck coefficient/electrical conductivity measurement system(Netzsch SBA458)was used to measure the electrical conductivity and Seebeck coefficient of the sample in argon atmosphere. The thermal conductivity of the sample was obtained according tok=DCpd, wheredis the geometric density of the sample. The diffusion coefficientD(Netzsch instruments/LAF457) perpendicular to the pressure direction of the sample was obtained by laser scattering method.
3. Results and discussion
3.1. Phase composition and microstructure
The phase purity and crystallinity of Ca3Co4O9samples with carbon nanotubes addition of different mass ratios were characterized by XRD. Figure 1 shows the XRD spectra of all samples. All samples are single-phase, and the major crystal phase matches with the standard JCPDS card(No. 21-0139) of Ca3Co4O9. No other peaks are detected,indicating that the purity of all samples is very high, and the content of carbon nanotubes is relatively small. It can also be seen from the figure that the diffraction peak in the (00l)plane is relatively strong, while other peaks are relatively weak. The results show that the samples have obvious preferred orientation in thecdirection, which is mainly caused by the preferential growth of grains on the plane perpendicular to the pressure direction during sintering. Simultaneously, with the increase of the amount of carbon nanotubes,the orientation of the sample in the(00l)direction decreases.Figures 2(a)-2(e)show the morphology of the samples added with different proportions of carbon nanotubes. It can be observed from the figure that the sample presents a sheet shape.It is found that the grain size does not change significantly with the increase of carbon nanotubes. The average particle size of the sample is 700-800 nm. Figure 2(f)shows the morphology of the sample with carbon nanotubes doping of 10 wt.% at a higher multiple.The filamentous carbon nanotubes in the sample are circled with a blue circle. The density and atomic ratio of Ca3Co4O9/xwt.% CNTs (x=0, 3, 5, 7, 10) samples are provided in Table 1. The density of the sample decreases with the increase in the content of carbon nanotubes (the theoretical density of Ca3Co4O9is 4.68 g/cm3).[25]After normalizing the atomic ratio,the content of carbon atoms in the sample increases with the increase of the amount of carbon nanotubes.
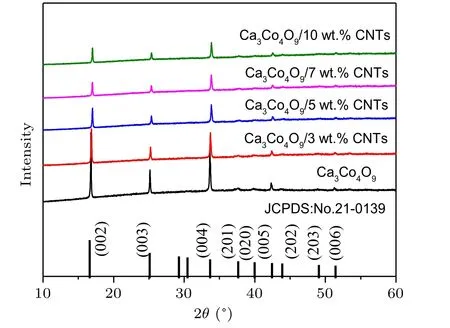
Fig.1. XRD pattern of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)sample.
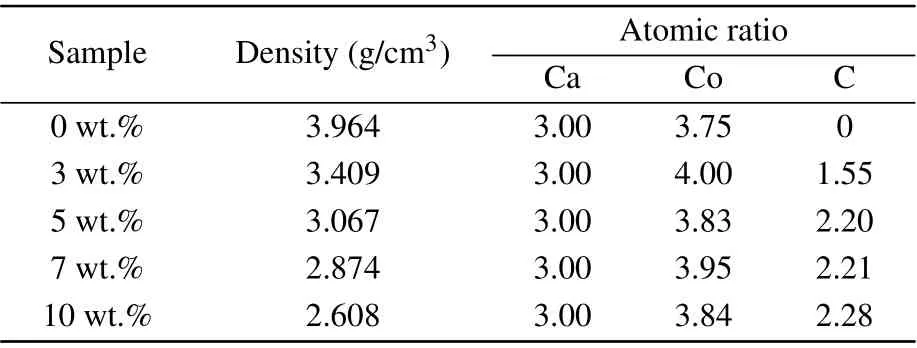
Table 1. Density and atomic ratio of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.

Fig.2. SEM images of sintered sample surfaces: (a)Ca3Co4O9,(b)Ca3Co4O9/3 wt.%CNTs(c)Ca3Co4O9/5 wt.%CNTs,(d)Ca3Co4O9/7 wt.%CNTs,(e)Ca3Co4O9/10 wt.%CNTs and(f)filamentous carbon nanotubes in Ca3Co4O9/10 wt.%CNTs are circled with a blue circle.
3.2. Electrical transport properties
The relationship between electrical conductivity and temperature of Ca3Co4O9/xwt.%CNTs(x=0,3,5,7,10)samples are exhibited in Fig. 3. Due to the limitation of the stability of carbon nanotubes, the test mainly studies the thermoelectric properties of samples from room temperature to 625 K. It can be observed from the figure that the electrical conductivity of all samples increases with the increase of temperature in the temperature range of 275 K to 625 K,showing significant semiconductor behavior. However, the conductivity of the sample with carbon nanotubes addition is significantly lower than that of the original sample. Although carbon nanotubes have high conductivity, it is mainly reflected along its length. In this study,the orientation of carbon nanotubes added to Ca3Co4O9is random, then its excellent conductivity cannot be brought into full play. The relationship between conductivity and resistivity can be expressed asσ=1/ρ. Adding carbon nanotubes to Ca3Co4O9sample introduces pore structure and interface, which increases the electron scattering center of the composite sample, increases the resistivity of the sample, that is, the electrical conductivity decreases,and the electrical conductivity of the composite decreases with the increase of carbon nanotube content.
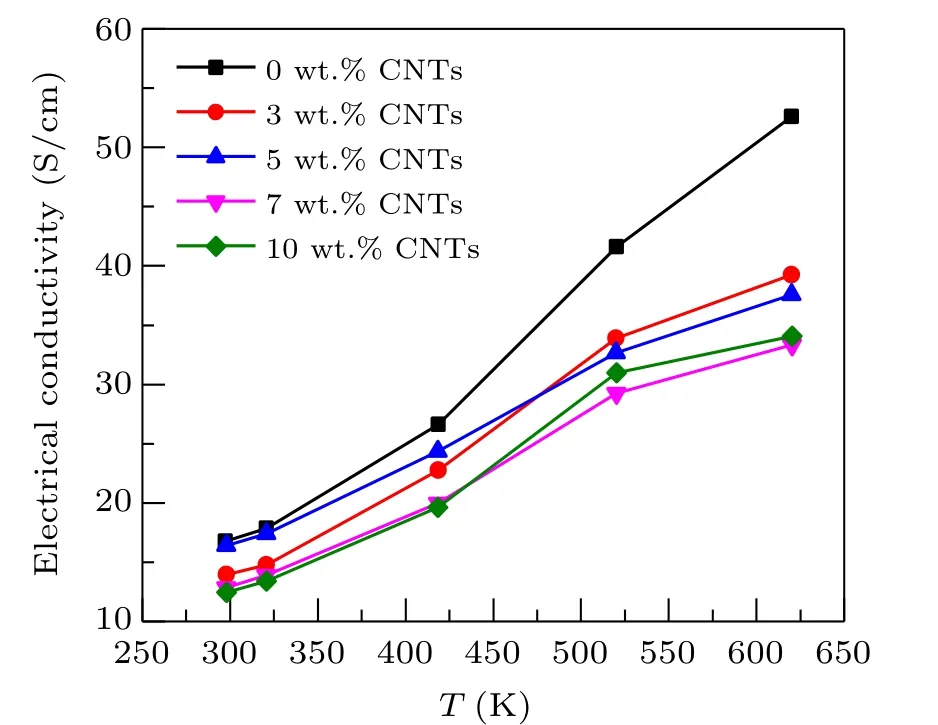
Fig.3. Relationship between the electrical conductivity and temperature of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.
Figure 4 shows the relationship between Seebeck coefficients and temperature of Ca3Co4O9samples with different contents of carbon nanotubes. The Seebeck coefficients of all samples in the figure increase with the increase of temperature.The Seebeck coefficients of all samples are positive,indicating that the samples are p-type semiconductors,dominated by hole conduction. The Seebeck coefficient increases monotonically with the increase of temperature,which may be related to the phonon traction effect,that is,the phonons in the semiconductor flow from the high-temperature end to the low-temperature end. Through the collision with the carriers, the phonons transfer energy to the carriers, forming the flow of carriers in the same direction as the phonon flow,to improve the Seebeck coefficient. Simultaneously,it can be observed from the figure that the Seebeck coefficient of the sample decreases with the increase of carbon nanotubes content. At 625 K,the Seebeck coefficient of the Ca3Co4O9/10 wt.%CNTs sample decreases to 136.85 µV/K, compared with 82.02 µV/K of the undoped samples,reduced by about 40%. For the composite semiconductor material of two substances,the Seebeck coefficient can be expressed as[26]
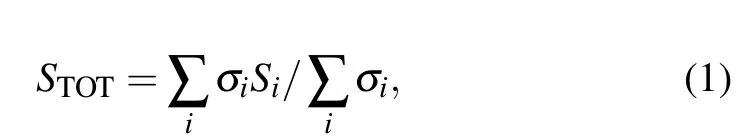
whereSTOTrepresents the total Seebeck of the sample,σirepresents the conductivity of different substances, andSirepresents the Seebeck coefficient of different substances. It can be seen from the formula that the conductivity has a great influence on the Seebeck coefficient. Carbon nanotubes have higher conductivity, that is, the denominator becomes larger,while the Seebeck coefficient of carbon nanotubes is smaller,and the molecular change is small.[27]Thus, the Seebeck coefficient of the composite sample is reduced.
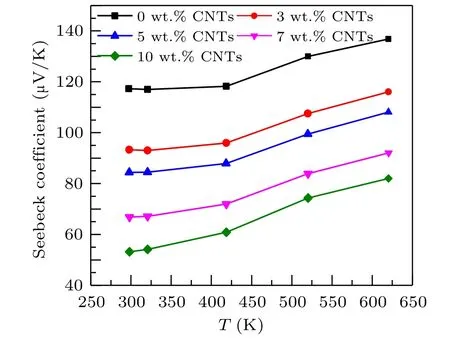
Fig.4. Relationship between the Seebeck coefficient and temperature of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.
Based on the measurement results of electrical conductivity and Seebeck coefficient,to evaluate the electrical properties of thermoelectric materials,the electrical properties part ofZT=σS2T/kis used,σS2,which is called the power factorPF(PF=σS2)of the material.The calculated power factor of Ca3Co4O9/xwt.%CNTs series samples is provided in Fig.5.The power factor increases with the increase of temperature which can be attributed the joint influence of electrical conductivity and Seebeck coefficient. In the whole temperature range,the power factor of the samples with carbon nanotubes added is lower than that of the original samples. At 625 K,the power factor of the undoped samples is 0.98µW/cm·K2. The power factor of Ca3Co4O9/10 wt.%CNTs samples decreases to 0.22µW/cm·K2.The above results show that doping carbon nanotubes will reduce the electrical properties of the materials.
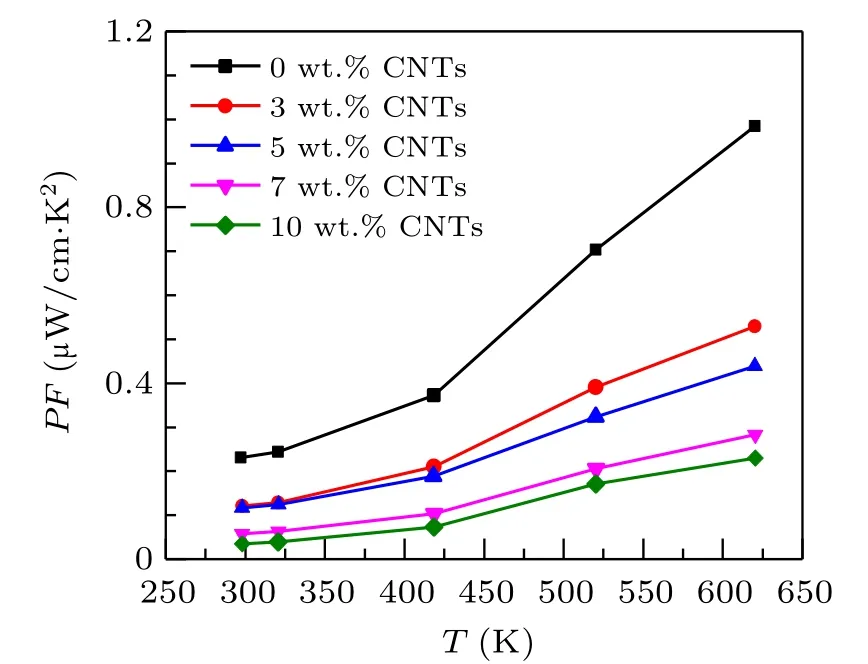
Fig. 5. Relationship between the power factor and temperature of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.
3.3. Thermal transport properties
Figure 6(a) shows the variation of the total thermal conductivity of the sample with temperature. The thermal conductivity of the sample with carbon nanotubes addition is significantly lower than that of the original sample. And the thermal conductivity decreases with the increase of the content of carbon nanotubes. For Ca3Co4O9/xwt.% CNTs system, in general,the total thermal conductivitykof the sample consists of two parts: the carrier thermal conductivitykcand phonon thermal conductivitykp, i.e.,k=kc+kp. The carrier thermal conductivitykcis related to the electrical conductivity via the Wiedemann-Franz equation,kc=LTσ, whereLis the Lorenz constant (L=2.45×10-8V-2·K-2), and the calculated value ofkccan be ignored for its relatively small value(Fig.6(b)). Therefore,kmainly depends onkp(Fig.6(c)). In the low order approximation,kp=1/3cvlp,wherec,vandlprepresent the specific heat capacity, phonon propagation velocity and average free path, respectively. Generally, doping will increasecand decreasevandlp. Moreover, the phonon propagation velocity is positively correlated with the average free path of the phonon. At 625 K, the thermal conductivity of the sample decreases from 1.527 W·m-1·K-1of Ca3Co4O9to 0.408 W·m-1·K-1of Ca3Co4O9/10 wt.% CNTs, which is decreased by about 73%.
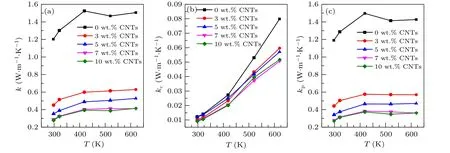
Fig. 6. Relationship between (a) total thermal conductivity k, (b) carrier thermal conductivity kc and (c) phonon thermal conductivity kp of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples with temperature.
The main factors affecting the thermal conductivity of composites include their own thermal conductivity, particle distribution of added phase, interfacial thermal resistance,porosity and so on. The thermal conductivity of carbon nanotubes is relatively high. The thermal conductivity of multi walled carbon nanotubes reaches 600-4000 W·m-1·K-1at room temperature. When adding high thermal conductivity carbon nanotubes to Ca3Co4O9, it is generally believed that the thermal conductivity will increase, while the actual measurement results decrease with the addition of carbon nanotubes. In this study,the particle phase of the composites obtained by fully mixing carbon nanotubes and Ca3Co4O9can be regarded as uniformly distributed, so the effect of particle distribution on it can be ignored.
According to Matthiessen’s law,the phonon thermal conductivity mainly depends on point defect scattering, grain boundary scattering,phonon-phonon scattering and resonance scattering.[28,29]The existence of composite interface will inevitably affect the thermal conductivity. Panget al.optimized the series parallel model based on the effective medium thermal conductivity theory, and gave the effective thermal conductivity of composite elements with interfacial thermal resistancekcomas[30]

wherek2is the thermal conductivity of the matrix material,k1is the thermal conductivity of the additive,V1is the volume fraction of the added phase,Ris the diameter of the added phase particles,andRBis the interfacial thermal resistance of the added phase in the composite. In this study, the particle size of Ca3Co4O9is about 700 nm,while the diameter of carbon nanotubes is only about 5 nm,which is much smaller than that of Ca3Co4O9and can be regarded as spherical particles.The effect of carbon nanotube addition on the effective thermal conductivity of Ca3Co4O9material can be discussed by using the model of formula (2). Therefore, for carbon nanotubes and Ca3Co4O9matrix composites,k2is the thermal conductivity of the matrix Ca3Co4O9without carbon nanotubes,k1is the thermal conductivity of carbon nanotubes,the carbon nanotubes added in the experiment are double-walled carbon nanotubes, the thermal conductivity is about 3000 W·m-1·K-1,V1is the volume fraction of carbon nanotubes,Ris the diameter of carbon nanotubes (5 nm), andRBis the interfacial thermal resistance of carbon nanotubes in the composites,According to a report of Cahill and Keblinski research group,the interfacial thermal resistance of carbon nanotubes is about 8.33×10-8m2·K·W-1.[31]By substituting the corresponding value into formula (2), the effective thermal conductivitykcomof Ca3Co4O9composites with different amounts of carbon nanotubes can be calculated when considering the interfacial thermal resistance. The calculation results are shown in Fig.7.
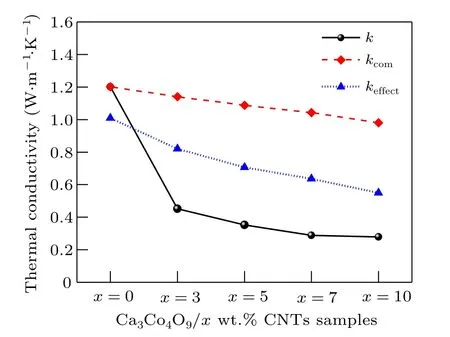
Fig.7. Relationship among kcom, keffect and k of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.
For ceramic samples, the effect of pores on the thermal conductivity of materials cannot be ignored. To study the effect of pores on thermal conductivity,Panget al.transformed the ideal composite into a single-phase solid material with effective thermal conductivity ofkcomand regarded the pore phase as one phase to build a model based on the model of formula(2),and deduced that the effective thermal conductivity(keffect)of the composite with voids and interfacial thermal resistance is[30]
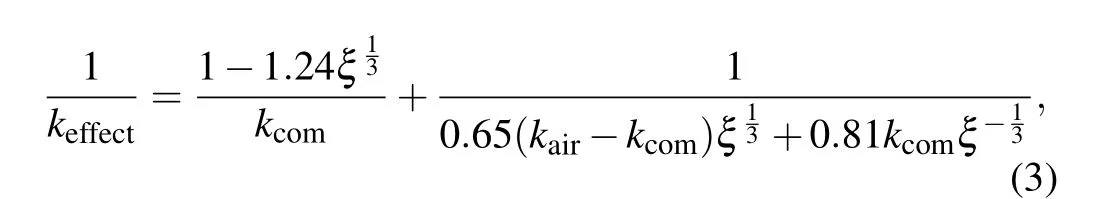
wherekairis the thermal conductivity of the stomatal phase,ξis the proportion of pore phase in the unit, that is, porosityξ=(ρ0-ρi)/ρ0,ρ0is the theoretical density of the base material,ρiis the density of each sample. In this study, the carbon nanotube with interface and Ca3Co4O9composite discussed in formula (2) are regarded as a single phase, and the pores are regarded as the second phase,that is,kairis the thermal conductivity of the pore phase(0.023 W·m-1·K-1),ρ0is the theoretical density of Ca3Co4O9(4.68 g/cm3),ρiis given in Table 1. Bring the above values into formula (3) to calculate the effective thermal conductivity of the composite containing pores and interfaces. The calculation results are given in Fig.7.
As shown in Fig. 7, when only the interfacial thermal resistance is considered, the effective thermal conductivitykcomvalue of carbon nanotubes and Ca3Co4O9composites decreases with the increase of the amount of carbon nanotubes,which is consistent with the experimentalk. The results show that the addition of carbon nanotubes into the interface hinders heat transfer and reduces the thermal conductivity of the composites. When the effects of interfacial thermal resistance and pores on the effective thermal conductivitykeffectof the composites are considered at the same time, the effect value also decreases with the increase of the amount of carbon nanotubes,and the decreasing trend is greater thankcomand closer to the experimental valuek,indicating that pores have a great influence on the effective thermal conductivity of the composites.In conclusion, adding carbon nanotubes to Ca3Co4O9introduces interfacial thermal resistance and pores,which plays an important role in reducing the thermal conductivity,indicating that adding carbon nanotubes is one of the effective ways to reduce the thermal conductivity of Ca3Co4O9.
3.4. Dimensionless figure of merit
Figure 8 shows the relationship between theZTvalue and temperature of Ca3Co4O9/xwt.% CNTs (x= 0, 3, 5,7, 10) samples . TheZTvalue is the result of the coupling of electrical conductivity, Seebeck coefficient and thermal conductivity. It can be seen from the calculation results that theZTvalues of the Ca3Co4O9/3 wt.% CNTs and Ca3Co4O9/5 wt.% CNTs samples increase significantly, and that of Ca3Co4O9/7 wt.% CNTs has little change. With the increase of the content of carbon nanotubes, theZTvalue of the Ca3Co4O9/10wt.% CNTs sample decreases. At 625 K,theZTvalue of the sample with the addition content of 3%is the highest, reaching 0.052. Compared with pure Ca3Co4O9samples at the same temperature,theZTvalue is increased by 29%. The sample with 3 wt.%CNTs has the best thermoelectric performance at 625 K.The above results show that an appropriate amount of carbon nanotubes is an effective method to improve the thermoelectric properties of Ca3Co4O9.
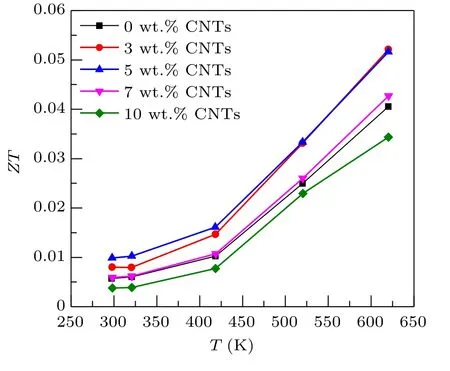
Fig. 8. Relationship between the ZT value and temperature of Ca3Co4O9/x wt.%CNTs(x=0,3,5,7,10)series samples.
4. Conclusions
We systematically studied the thermoelectric properties of Ca3Co4O9/xwt.% CNTs (x= 0, 3, 5, 7, 10) composite samples prepared by sol-gel method. XRD and SEM showed that the samples were single phase and showed sheet like morphology. The electrical conductivity and Seebeck coefficient of all samples with carbon nanotubes addition were lower than those of the original sample. Proper addition of carbon nanotubes can effectively reduce its thermal conductivity. At 625 K, the thermal conductivity of the sample (Ca3Co4O9/10 wt.% CNTs) decreased from 1.527 W·m-1·K-1of undoped samples to 0.408 W·m-1·K-1,which decreased by about 73%. When the addition content was 3%, theZTvalue reached 0.052, which was 29%higher than that the original sample. These show that an appropriate amount addition of CNTs can reduce the thermal conductivity of Ca3Co4O9ceramic samples and improve the thermoelectric properties.
Acknowledgement
This work was supported by the National Natural Science Foundation of China(Grant No.51836009).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Helium bubble formation and evolution in NiMo-Y2O3 alloy under He ion irradiation
- Dynamics and intermittent stochastic stabilization of a rumor spreading model with guidance mechanism in heterogeneous network
- Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
- Low-overhead fault-tolerant error correction scheme based on quantum stabilizer codes
- Transmembrane transport of multicomponent liposome-nanoparticles into giant vesicles
- Molecular dynamics simulations of A-DNA in bivalent metal ions salt solution
