双向等压圆形巷道塑性区径向位移时变解求解及岩爆防治分析

樊宝杰， 赵伏军， 吴秋红， 刘永宏， 王 斌

(1.湖南科技大学 资源环境与安全工程学院， 湖南 湘潭 411201； 2.湖南省城市地质调查监测所， 湖南 长沙 410000)

1 研究背景

20世纪90年代，有关时变力学的研究逐渐兴起。时变力学是一门研究物体内部参数随时间变化的力学学科。目前大多力学学科的基本理论和控制方程都是建立在研究对象外部条件的变化上，如施加的载荷场、温度场、能量场随时间变化，但内部参数如几何形状、物理性质、边界条件等在研究过程中总认为是恒定不变的[1]。随着我国科学技术和基建的高速发展，研究对象内部的结构参数和力学特征随时间变化的重要性日益凸显，如建筑物长期在风力和自重作用下内部结构的疲劳损伤随时间随机变化[2]；桥梁根据桥面通过车辆的总数和重量的不同，桥梁的受力、几何形状、边界条件等都随时间具有不确定性[3-4]。国内外学者对于时变力学的相关问题进行了大量研究。Su等[5]在分数麦克斯韦模型和时变粘度麦克斯韦模型之间建立了等效粘弹性，揭示了分数粘弹性模型的物理意义；Wu等[6]分析了时变网络，将其用于矿井突水疏散规划，为人员逃生提供了导航；何文正等[7]研究了隧道衬砌在硫酸盐侵蚀下的时变力学特征，得到受侵蚀的混凝土衬砌承载能力明显降低，发生偏心破坏的几率随时间增加的结论；谷中元等[8]研究了浅埋空区群结构的时变力学特征，发现空区群内矿柱两侧横向位移随时间增大，空区群顶板下沉量随时间加速增加；张贤达[9]利用时变理论分析了隧洞内锚杆支护-围岩耦合系统的力学效应，结果显示加强支护可减少围岩变形，围岩位移量对围岩本身的粘滞性系数比较敏感；王立波等[10]基于时变力学研究了近海钢筋混凝土结构抗震性能的劣化规律，发现其极限抗震能力随时间近似呈线性劣化关系，劣化速率随设防水平的降低而增大；倪卫达[11]选取地震和库水作为外部载荷，结合土体内部时变强度参数，开展了边坡动态变化特点的研究，将边坡稳定系数拓展为与时间有关的函数。纵观上述研究，地下空间工程领域中有关时变力学的研究相对较少。地铁、矿山巷道等地下空间工程，具有周期长、规模大、工序复杂繁琐等特点，各种地质灾害频发，施工过程中不同阶段结构的完整性和承载受力情况均不相同，工程设计和安全生产的研究亦需考虑时间变量[12-15]。在巷道施工中，随着掘进面不断推进，巷道围岩的边界条件、围岩岩性、受力特征等参数亦随时间不断变化，巷道的弹性时变解、弹塑性时变解、径向位移时变解对于了解巷道的稳定状态和防治岩爆等地质灾害具有重要意义。

2 双向等压圆形巷道模型建立及其时变解求解

线弹性、边界问题可利用经典力学代入对应的时间求其时变力学解。非定常(黏性、渗流、固结)、非线性(物理、几何边界、非线性耦合)、动力学等时变问题与不同时刻耦合是非常复杂的。深部巷道岩爆的发生实质可归结于几何边界随时间的变化或开挖引起围岩岩性的弹塑性转变，所以巷道的弹塑性时变解和径向位移时变解对于研究岩爆问题至关重要。

2.1 双向等压圆形巷道模型建立及岩石本构关系选取

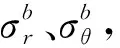
图1 圆形巷道弹塑性力学计算模型

岩石本构方程如图2中所示的双线性应力-应变关系。具体如下，

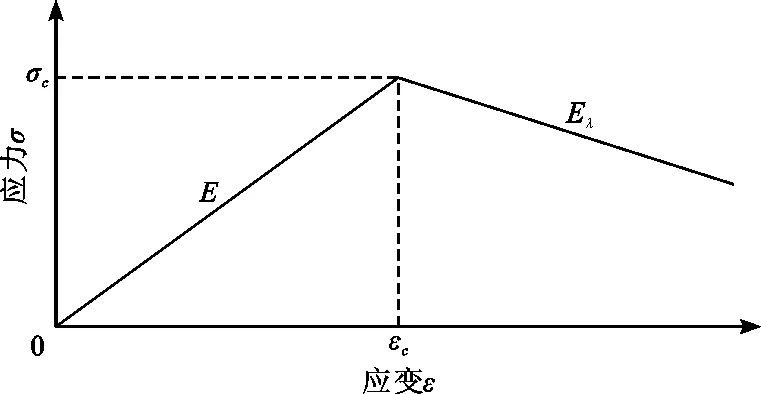
图2 岩石双线性应力-应变关系

弹性阶段：

σ=Eε(ε<εc)

(1)

式中：σ为岩石所受应力，MPa；E为岩石弹性模量，MPa；ε为岩石在应力σ下对应的应变，%；εc为岩石在单轴峰值应力σc下对应的应变，%。

软化阶段：

σ=σc-Eλ(ε-εc) (ε>εc)

(2)

式中：σc为岩石峰值强度，MPa；Eλ为降模量，即峰后单位应变增长对应的应力下降值，MPa。

该本构关系可用来研究脆性煤岩的力学问题，岩石脆性越强，Eλ越大；脆性越弱，Eλ越小；Eλ=0为理想塑性材料[16]。

2.2双向等压圆形巷道弹性时变解

由弹性理论可求得双向等压圆形巷道弹性解(平面应变问题)为[17]：

(3)

(4)

式中：σr为围岩径向应力，MPa；σθ为围岩切向应力， MPa；p0为无限远处初始地应力，MPa；a0为巷道半径，m；r为式中应力及其位移所对应的围岩到巷道轴线的距离，m；ur为围岩的径向位移，m；μ为泊松比。

假设塑性区内体积不可压缩，取μ=1/2，则εr+εθ+εz=0，径向位移解为:

(5)

式中：εr为围岩径向应变，%；εθ为围岩切向应变，%；εz为围岩轴向应变，%；G为剪切模量，MPa。

将以上结果引入时间变量t，把时不变弹性解中的物理或几何参数替换为相应时变函数，则无体积变形时的弹性时变解为：

(6)

(7)

式中：a(t)为时变巷道半径，m。

2.3双向等压圆形巷道弹塑性时变解及径向位移时变解

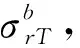
(8)

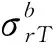
r轴、θ轴所在平面为巷道横截面，r轴、θ轴相互垂直；z轴位于弹性区和塑性区的交界面内且垂直于巷道横截面。

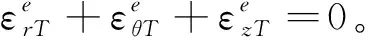
(9)

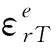
(11)

将公式(11)代入公式(10)可得：

(12)

2.3.2 双向等压圆形巷道塑性区时变力学解 对于塑性区，其基本方程如下：

(1)几何方程

(13)

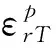
(2)平衡方程

(14)

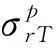
(15)

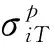
将εc=σc/E代入公式(15)可得峰值后的本构关系为：

(16)

(17)

公式(17)的通解为：

(18)

将公式(18)代入公式(13)可得：

(19)

由公式(19)可得塑性区的等效应变强度为：

同时由公式(16)可得塑性区的等效应力强度为：

(21)

2.3.3 双向等压圆形巷道塑性区径向位移时变解 根据弹、塑性区交界面的等效应力强度相等且等于σc，此时r=b(t) ，联系公式(20)、(21)和(12)可得：

(22)

式中：b(t)为塑性区时变半径，m。

将公式(22)代入公式(18)得到塑性区的径向位移为：

(23)

由公式(20)和(21)得到：

(24)

(25)

(26)

式中： e为自然常数。

2.4时变速度相关性分析

设圆形巷道开挖半径为a0，塑性区边界以速率c向外扩展T时间后结束时变，塑性区半径变为b(T)=b0，则T=(b0-a0)/c。

(27)

设塑性区半径的时变函数为:

(28)

当t∈[0，T]时，塑性区径向位移解为

(29)

3 实例计算与分析

以陕西省汉中市宁强县铁锁关镇戚家垭隧道为例[18]，该隧道开挖断面近似圆形，半径为7.38 m，将相关数据代入公式(29)可得到图3和表1。

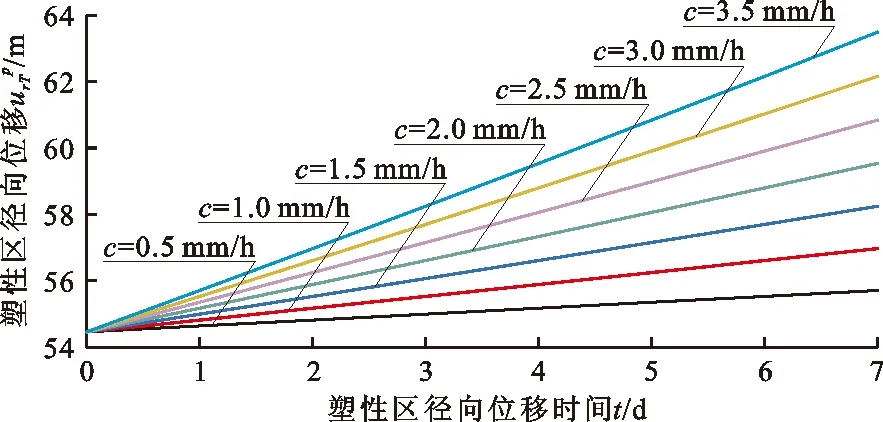
图3 塑性区边界不同移动速率下相同半径巷道塑性区径向位移随时间变化(a0=7.38 m)

当塑性区边界移动速率c较小时(ct相对于a0可忽略)，塑性区内岩体径向位移随时间的增长近似为线性增大；分析公式(29)知，塑性区边界移动速率c较大时，塑性区内岩体径向位移随时间的增长呈抛物线状增大。

表1为相同塑性区边界移动速率下不同半径巷道塑性区径向位移。由表1和公式(29)可知，相同边界移动速率同一时间塑性区的径向位移主要受巷道半径影响，巷道半径越大，则塑性区径向位移越大。因此，大断面巷道的一次性全断面开挖易造成巷道围岩塑性区径向位移较大，从而诱发一系列地质灾害。

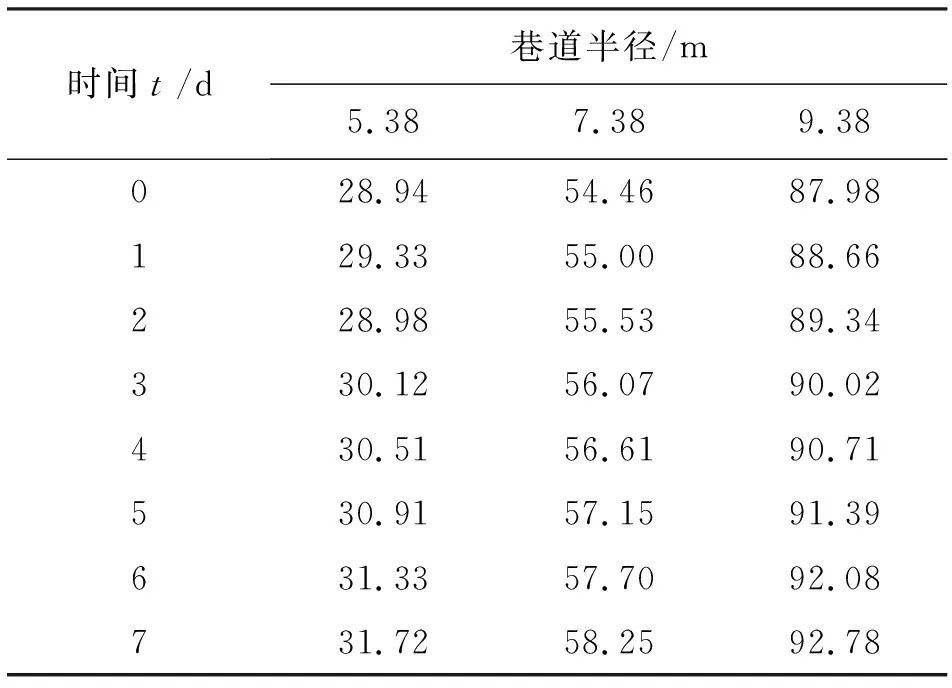
表1 相同塑性区边界移动速率下不同半径巷道塑性区径向位移(c=1.5 mm) m

根据文献[16]针对圆形巷道稳定性动力准则的分析，可以得到临界塑性软化区深度的表达式如公式(30)所示。

(30)

式中：ρ*为临界塑性软化区深度，m；a0为巷道半径，m；E为弹性模量，MPa；Eλ为降模量，MPa。

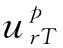
4 讨 论

岩爆是由于开挖和扰动引起的一种突然和剧烈的围岩破坏形式，触发时以岩石薄片、岩块、岩屑抛射的形式出现，并伴有嘶嘶声或轰鸣声[19-21]。岩爆具有随机性和剧烈性，容易造成严重的人员伤亡、机械损伤和经济损失[22-24]。由于岩体的物理力学性质、地质条件和人为干扰因素的相互耦合和多变性，岩爆机理十分复杂。岩爆往往在开挖加卸载完成后，滞后一段时间才发生，这无疑增加了岩爆灾害的隐蔽性和破坏性，增大了对岩爆预测、预报及防治的难度。因此在研究有岩爆危险倾向的煤岩体力学行为时，必须考虑时间因素的影响。大量工程实践表明，岩爆的发生是与时间相关的。文献[25]根据现场监测结果，总结岩爆频率与爆破间隔时间的关系见图4，大量观测记录表明中等以上岩爆区的岩爆在放炮后1 h和6～7 h时比较频繁。

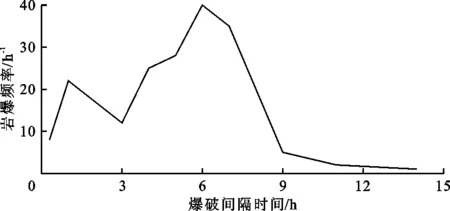
图4 岩爆频率与爆破间隔时间的关系

岩爆时间效应的研究近年来才得到重视。Zhang等[26]通过单轴恒载试验研究了岩石破坏的时间特性，结果显示在高应力条件下，岩石破坏具有明显的时间特性，与裂纹扩展的时间特性相对应，当损伤积累到一定程度时，岩体失稳，进而引发岩爆。徐鹏飞等[27]研究了不同应力水平下砂岩单轴压缩滞后破坏的特征，得到随应力水平提高，砂岩孕育岩爆的时间呈指数降低的结论。翁磊等[28]利用数值模拟分析了深埋巷道围岩板裂化和屈曲型岩爆的发生机制，发现巷道围岩薄板结构形成后，随时间增加其蠕变变形量达到极限后，发生滞后岩爆现象。纵观其研究状况，可将岩爆时间效应的研究分为两种类型：加载时间增加导致的岩爆和岩体强度随时间衰减引发的岩爆，其本质还是围岩塑性区径向位移达到了临界塑性软化深度，所以在临界塑性软化深度确定的情况下，应尽量减小塑性区径向位移。分析公式(29)可知，利用支护结构降低塑性区径向位移速率、满足使用功能时尽量采用较小半径的巷道、缩短塑性区径向位移时间，可有效控制塑性区径向位移，对防治岩爆起到了积极作用。成兰铁路平安隧道D8K169+000～D8K168+950段在施工过程中岩爆频发，现场支护方案由最初的常规锚网支护+拱墙格栅拱架支护调整为加强型锚网支护(5 m 长锚杆)+全环 I18 型钢拱架支护，现场岩爆情况得到了初步防治[29]。可见围岩应力重分布初步完成后，及时加强支护减小塑性区径向位移速率、控制塑性区径向位移时间，对岩爆防治具有显著效果。杨敏等[30]对宜昌某磷矿的岩爆特征进行了研究，发现其采区几何尺寸大于开拓巷道，采区发生岩爆的频率和烈度明显高于开拓巷道。岩爆时间效应的研究无疑会对岩爆的研究提供新的认识论和方法论，这对于开拓和发展岩爆理论，准确预测岩爆，都具有极为重要的理论意义与现实意义。

5 结 论

本文利用时变力学理论研究了双向等压圆形巷道的塑性区径向位移时变解，对岩爆的防治进行了时变分析。主要结论有以下几点：

(1)结合时变力学和双向等压圆形巷道塑性区的几何方程、平衡方程，得到双向等压圆形巷道的弹塑性时变解。根据弹性区和塑性区交界面等效应力相等，求解得到双向等压圆形巷道塑性区径向位移时变解。

(2)根据双向等压圆形巷道塑性区径向位移时变解得到，塑性区边界移动速率c较大时，随着时间的增长，塑性区径向位移显著增加。塑性区边界移动速率相同且在同一时刻时，巷道半径是影响塑性区径向位移的主要因素。

(3)临界塑性软化深度确定的情况下，降低塑性区径向位移速率、选取较小半径的巷道、缩短塑性区径向位移时间，可有效控制塑性区径向位移，可对防治岩爆起到积极作用。双向等压圆形巷道塑性区径向位移时变解对岩爆的研究具有启发意义。