基于混合-浓度模型的泄洪洞内水流掺气数值模拟研究
2022-04-12练继建任盼红刘东明何军龄
练继建, 任盼红, 刘东明, 何军龄
(1.天津大学 水利工程仿真与安全国家重点实验室, 天津 300350; 2.天津大学 建筑工程学院, 天津 300350)
1 研究背景
水体中掺入空气形成水气二相流是水利工程中常见的现象。水体掺气对泄水建筑物有利有弊,有利的方面主要有:水体掺气可以降低脉动压强[1],还可以减免空蚀破坏,通过采用掺气设施使过水建筑物表面水流发生强迫掺气从而保护泄水建筑物[2-4]。不利的方面主要有:水体掺气会使水深增加[5-6],若是对水体掺气量估计不足,会导致开敞式溢洪道边墙设计高度偏低,从而使得掺气水流越过边墙,危害泄水建筑物安全,或导致溢洪洞和泄洪洞洞顶余幅减小,通气不畅,从而造成泄水建筑物的损坏[7-8]。泄洪洞与溢洪道的不同之处在于泄洪洞中水体掺入的空气并非直接来自于大气,而是大气先经补气洞流入泄洪洞中,随后部分空气掺入水体中,余下部分则随水流流出泄洪洞[6,8]。影响洞内掺气特性的因素不仅包括来流流速、来流水深及水流流态等水力因素,还包括泄洪洞几何形态和闸门型式等结构布置因素[9]。
多位学者基于模型试验对洞内掺气进行了研究。Hohermuth等[10-12]基于来流水头达30.0 m、水槽长度达20.6 m的模型试验对洞内掺气进行了研究,发现空气需求量随着闸门后收缩断面弗劳德数的增加而增加,且掺气浓度与水流流速等水力参数均表现出与明渠流掺气相似的特性。Aydin[13]通过建立闸门关闭后水流的非恒定数学模型,得到了通风井内的空气流量以及闸门后压力随时间的变化规律。Speerli等[14]基于隧道物理模型试验,研究了不同工况下隧道内高速水流的水-气特征,并分析了水体中空气浓度的发展过程,得到了计算最大空气浓度的公式。岳书波等[15]对高速明流泄洪洞进行了分析与研究,发现闸室处的进气量随着闸门后水流弗劳德数的增大而增大。何佳等[16]对龙落尾泄洪洞起始段掺气设施进行了试验研究,发现随着工作水头的增加,过坎弗劳德数先减小后增大。物理模型试验一般仅满足重力相似准则,难以反映原型水体的表面张力和粘滞力,造成模型试验存在难以忽略的缩尺效应[17-18]。
近年来,计算机技术快速发展,数值模拟使得研究掺气水流的手段更加丰富[19]。黄宗柳[20]和Tang[21]采用数值模拟方法对明渠自掺气水流与破碎波掺气进行了计算,得到的掺气浓度与试验数据[22]吻合良好。针对隧道内不同条件下气流量的计算,Yazdi等[23]基于FLUENT对平板闸门后隧洞中的高速水流进行了三维数值模拟研究,并推导了关于隧洞内补气量和水流上方空气速度的公式。张法星等[24]采用标准k-ε紊流模型和VOF(volume of fluent model)方法对糯扎渡水电站泄洪洞进行了模拟计算,验证了k-ε紊流模型结合VOF方法可以用于预测大型泄洪洞的需气量。邓军等[25]采用FLUENT对某泄洪洞进行了计算,得到的压强和通气设施进气量等参数的计算结果和模型试验对比较好。此外,李玲等[26]采用k-ε紊流模型和VOF方法对溪洛渡泄洪洞进行了数值模拟研究,得到了沿程水面线以及底板中心线的压力分布。罗永钦等[27]对溪洛渡水电站的一条泄洪洞进行了数值模拟研究,结合模型试验数据,认为分段计算方法对于高流速、大梯度泄洪洞问题来说可以提高计算效率。Wei等[28]对隧道中的自由面水流供气特性进行了数值模拟研究,在不考虑掺气的条件下,提出了水流上方平均风速的计算公式,其平均误差为±25%。王孝群[8]采用改进的拖曳力模型对补气洞的补气量进行了计算,总体误差近20%。刘嘉夫等[29]与李明达等[30]分别基于FLOW-3D、FLUENT对掺气水流进行了数值模拟研究,计算结果同样与试验数据存在误差。针对以往数值模拟结果存在误差这一问题,本文基于自主开发的NEWTANK[31]数值模型,构建了研究掺气问题的混合-浓度模型,通过有限差分方法进行离散并求解,对洞内掺气试验进行了数值模拟计算,并探究了不同来流水头对水流流速和掺气浓度等参数的影响。
2 数值模型建立
2.1 混合模型
本研究针对的是洞内掺气水流,水体和气体的速度均小于声速,因此采用不可压缩流体的控制方程。采用的混合模型首先对除重力项外的其他项进行了水-气两相之间的平均,获得混合流场和混合压力场;然后采用基于雷诺平均的方法简化流场内的紊动发展过程,这种方法计算量小,运算速度快。混合模型具体表达式如下:
连续性方程:
(1)
动量方程:
(2)
式中:下标i、j=1,2,3分别表示x,y,z3个方向;um为混合流体的速度,m/s;t为时间,s;pm为混合流体的压强,Pa;ρ0为流体背景密度,kg/m3;ν为分子的运动黏滞系数,m2/s;νt为混合流体的紊动黏滞系数,通过紊流模型来获取,m2/s;ρm为混合流体的密度,kg/m3;g为重力加速度,m/s2。
重力项可通过下式进行化简,体现了掺气水流中空气与水体间的相互作用:
(3)
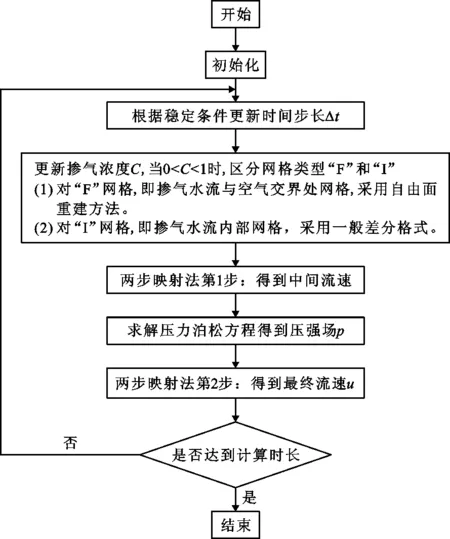
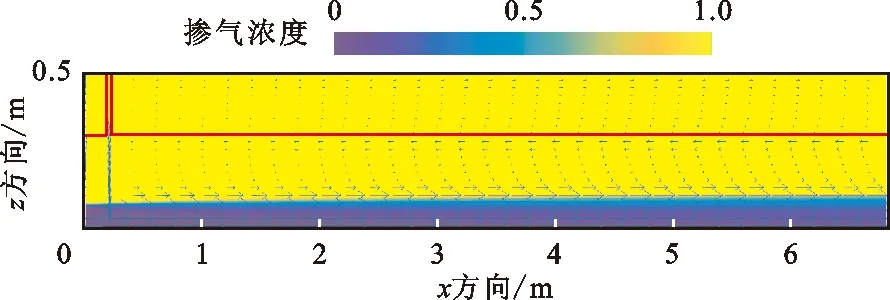
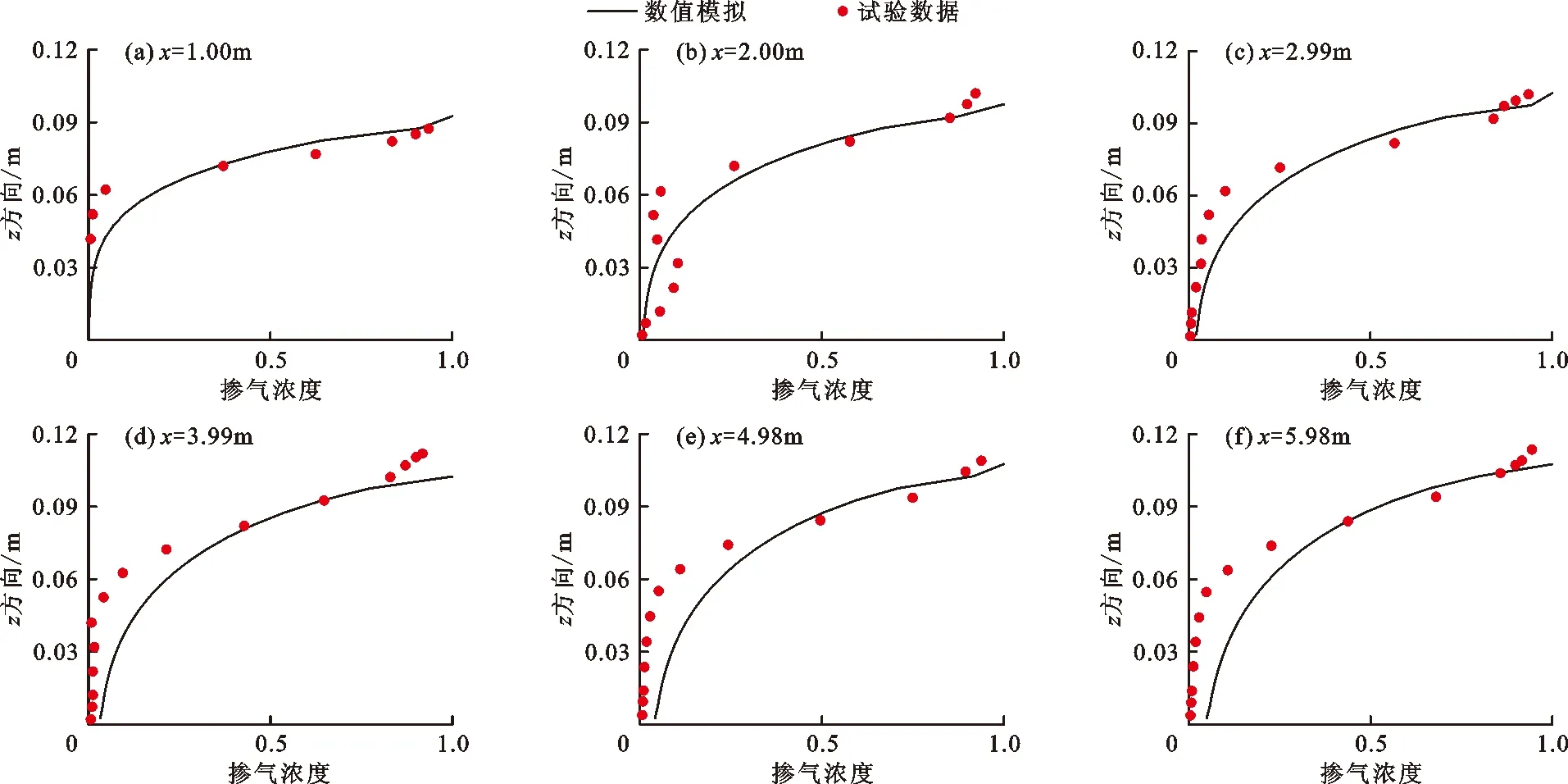
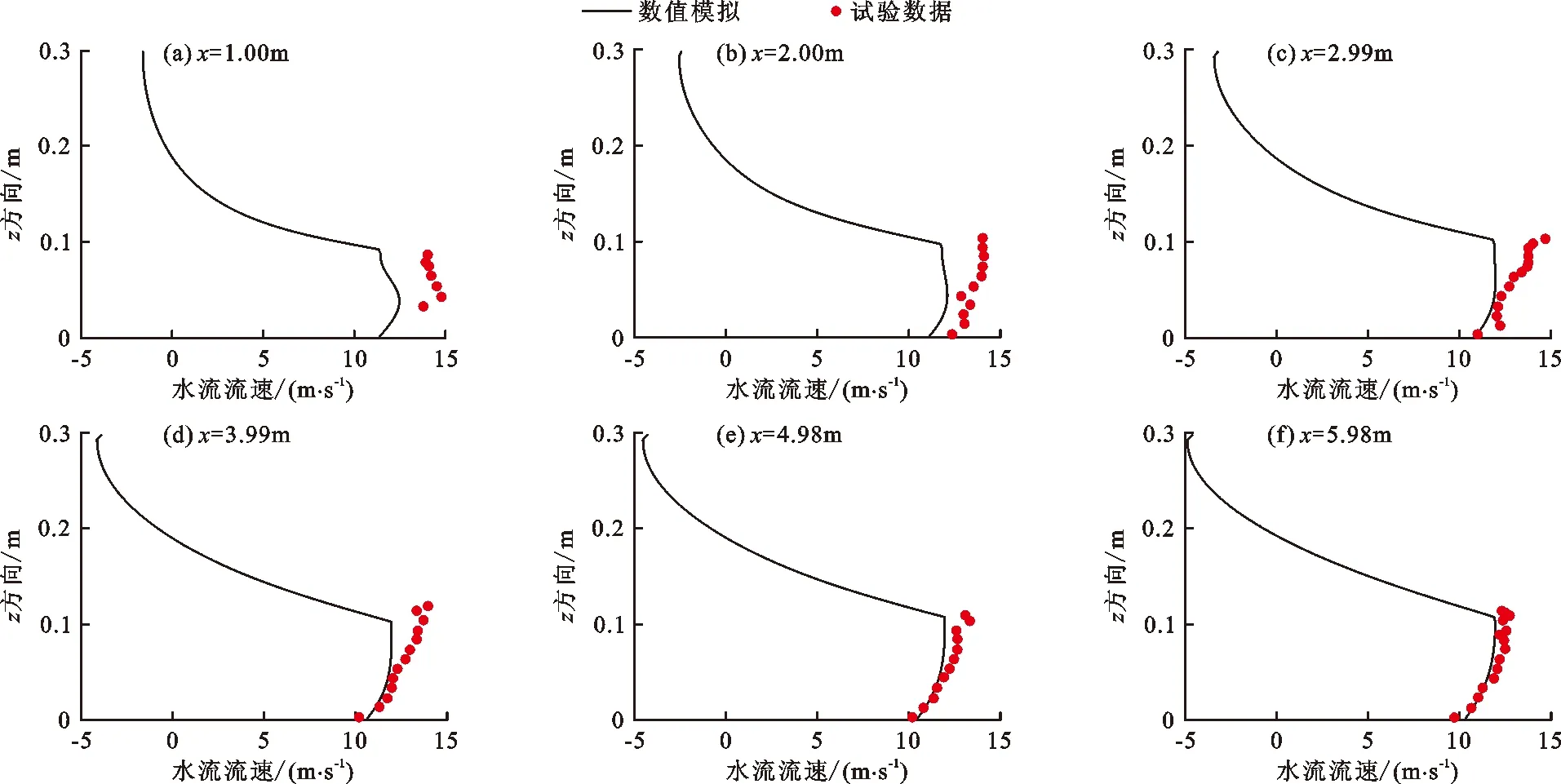
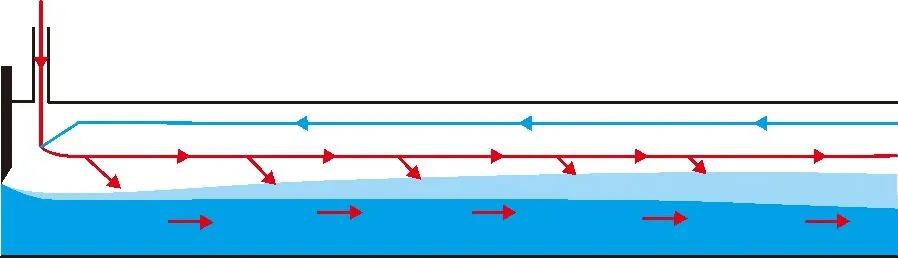
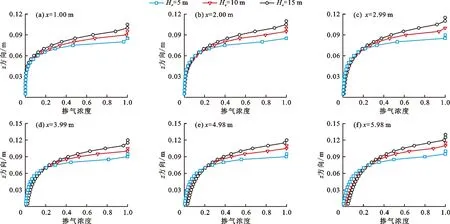
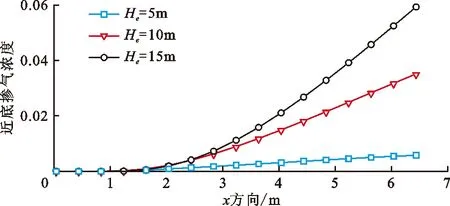
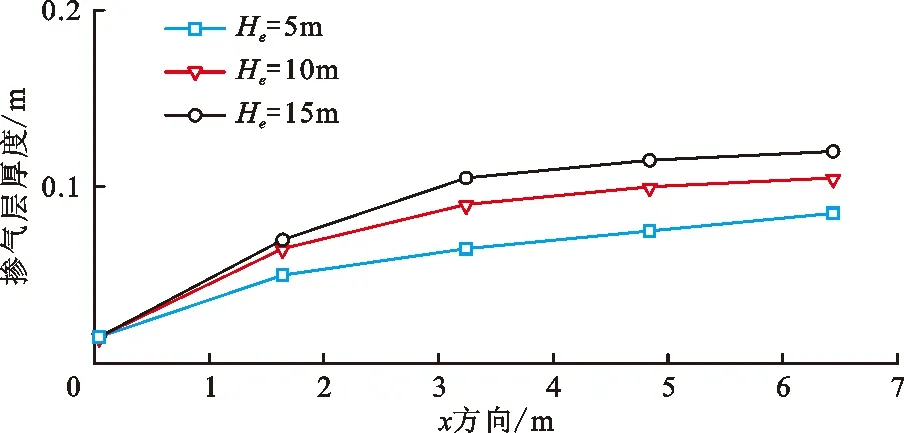
式中:C为每个网格中空气所占体积比,即掺气浓度。当C=1时,表示该网格中充满了空气;当C=0时,表示该网格中充满了水体;当0 将公式(3)代入公式(2)中,动量方程最终可表示为如下形式: (4) 为方便表示,后续水-气混合相关参数均无下标“m”,但依旧代表各相流体的混合量。 紊流模型采用应用较为广泛的k-ε两方程模型,具体表达如下: (5) (6) (7) (8) 式中:k为紊动动能,m2/s2;ε为紊动耗散率,m2/s3;Pb为浮力制造项,m2/s3;Prt取常数为0.85;σk、σε、C1ε、C2ε、C3ε、Cd均为经验系数,分别取值为σk=1.0、σε=1.0、C1ε=1.44、C2ε=1.92、C3ε=1.44、Cd=0.09。 本文采用的浓度模型[32]不考虑气体在水体中的溶解,亦不考虑各相流体间的化学反应,用于追踪自由液面位置以及获取掺气水流内部的掺气浓度分布信息,具体表达式如下: (9) 式中:σa为气体的扩散系数,表示紊动和气泡间的相互作用,在此其值取为1;ub为各相流体间的相对滑移速度,m/s。 Haberman等[33]提出了单个气泡在静水中的上浮速度计算公式: (10) 式中:ub0为气泡在静水中的上浮速度,m/s;Da为气泡直径,m;σt为表面张力,在此式中其值取为0.073 2 N/m。 然而,气泡在高速水流中的上浮速度的影响因素要比静水中复杂很多。当水流紊动作用剧烈时,紊动会将大气泡撕裂成小气泡,气泡互相接触、干扰,导致气泡间的碰撞、变形、破碎与聚并,造成气泡动能的损失,从而造成气泡上浮速度减小。在浮力作用下气泡倾向于向水体自由面上浮,在湍流扩散作用下气泡倾向于从高浓度区域移动到低浓度区域,当周围水体中均含有空气时,掺气浓度梯度减小,造成气泡上浮速度减小。为尽量体现紊动水流中的气泡上浮情况,本文建立的数值模型采用的气泡上浮速度同时考虑了紊动作用和掺气浓度的影响[20],计算公式如下所示: (11) 本数值模型的计算流程如图1所示。 图1 数值模型计算流程图 高水头结构物出口处常配置闸门,从闸门后流出的水流会带走大量空气,易导致负压,从而引发空蚀空化等问题。通过通风口提供充足的空气可有效缓解该问题,然而,尽管通风口对闸下出流的安全很重要,但关于这方面的设计研究却很少。Hohermuth[12]在苏黎世联邦理工学院水力学、水文学和冰川实验室进行了关于明流隧洞内水流掺气特性的物理模型试验研究,试验中,进口水深通过不带闸门槽的矩形尖顶闸门进行控制,闸门最大高度为0.25 m,明流隧洞宽度为0.2 m,高度为0.3 m,隧洞坡度为0.04。靠近闸门处连接一个圆形通风口,其直径为0.1 m。本文对上游来流水头为10 m(相应的单宽流量为0.88 m2/s),隧洞长度为6.6 m,闸门开度为40%的试验工况进行了数值模拟计算。 依据试验中物理模型的设置以及水流的来流条件,将数值算例计算域设置为6.8 m×0.5 m,并采用均匀网格进行离散。在x和z方向分别设置均匀网格170和100个,最小网格尺寸分别为0.040和0.005 m。在数值模拟过程中,采用坐标变换的方法,将原来倾斜的隧洞变成水平。z方向位于闸门处,垂直于槽底,x方向与隧洞底部重合。上游通风口设置在距离进口0.2 m的位置,由于通风口采用圆形截面,而隧洞采用矩形截面,因此可通过圆形面积除以隧洞宽度从而求得通风口的等效长度,即0.04 m。进口依据工况条件给定水深和水流流速,其中流速大小通过闸门开度和流量计算求得;出口处给定自由出流;底部采用墙边界条件;顶部给定压力进口。洞内水流掺气数值模型边界条件示意图见图2。 图2 洞内水流掺气数值模型边界条件示意图 数值模拟得到的掺气浓度和流场分布如图3所示。由图3可见,水流自闸门流出后,由于水体流速较高,紊动作用剧烈,空气逐渐掺入水体中,使水深逐渐增大。随着水流流向下游,掺气量逐渐增多,水深继续增大,最后达到相对稳定状态。 图3 掺气浓度和流场分布数值模拟结果 物理模型中,在x=1.00 m、x=2.00 m、x=2.99 m、x=3.99 m、x=4.98 m和x=5.98 m 6个断面进行掺气浓度和水流流速的测量。掺气浓度的数值模拟结果与试验数据对比如图4所示。 图4 掺气浓度数值模拟结果与试验数据对比 由图4可看出,掺气浓度的数值模拟结果与试验数据总体上较为吻合,仅局部存在差异。靠近进口位置的隧洞底部掺气浓度与试验数据吻合程度较高,而靠近出口位置处,底部的掺气浓度数值模拟结果大于试验结果,分析其原因是由于底部气泡上浮速度被低估,导致气泡不能及时逸出水面,造成数值模拟计算的掺气浓度比试验值偏大。 x=1.00 m断面数值模拟计算得到的掺气水深略大于试验值,其他断面处数值模拟计算得到的掺气水深均略低于试验值。差异的原因可能来自两个方面:一是距闸门较远位置靠近自由面的气泡上浮速度在数值模拟计算中被高估,使得气泡过早地逸出水面,造成水深偏低;二是相较于数值模拟计算得到的相对光滑自由表面,在模型试验实际过程中,由于水流流速较大,紊动程度较高,掺气过程的发生使得自由面不规则,波动的自由面掺杂着飞溅而出的小水滴,从而造成掺气水深偏大。 各断面处掺气浓度分布形状基本一致:在低掺气浓度区域(C<0.2),掺气浓度随深度的变化较为明显;在高掺气浓度区域(C≥0.2),即靠近水-气自由面位置,掺气浓度变化梯度较小,随水深变化不明显。x=2.00 m处靠近隧洞底部的试验数据局部突然增大是由于模型试验自身突出的接缝而产生的,在数值模型的设置中此处无法正确建模,因而造成数值模拟计算结果和试验数据存在较大差异。 6个断面处水流流速的数值模拟结果与试验数据对比如图5所示。 由图5可看出,在距离入口较近的位置,数值模拟得到的速度比试验值偏小;随着与入口位置距离的增加,差异逐渐减小;直至在靠近出口处(如x=5.98 m)差异基本消失,此时数值模拟得到的流速和试验数据几乎重叠。气泡大小随时间和空间的变化而变化,而本数值模型选取的固定气泡直径或许更加接近下游水流中的真实情况,因而造成这种差异沿程变化的现象。模型试验只给出了掺气水流的混合流速,而未给出空气的速度,由图5数值模拟计算结果可明显看出:仅在掺气水流上方一定高度,空气是流向下游出口方向的,而在靠近隧洞上壁面位置,存在与水流流向相反的气流,且靠近上壁面位置的气流速度随着与入口位置距离的增大而逐渐增大。在x=1.00 m处空气速度达到了-2 m/s左右,而在x=5.98 m处空气速度接近-5 m/s,随着与入口位置距离的逐渐增加,掺气水流的水深逐渐增加,因而逆向补气区域高度逐渐降低,由于逆向补气量是恒定的,因而造成气流速度逐渐增大。 图5 水流流速数值模拟结果与试验数据对比 前文中图3显示了此工况下计算域内的流场分布情况。空气自上游通风孔进入隧洞后,靠近水体的部分空气从通气孔位置流向下游出口,与此同时还存在隧洞出口处的逆向补气,这相反方向的两股气流在洞内形成一个大的逆时针气流旋涡。进口处流出的水流因流速高、紊动大,洞内的部分空气被掺入水体中,并带向下游,导致负压产生,在压差的作用下,上游通风口将外部大气带入洞内。若不考虑水流的拖曳作用,在压差的作用下空气会从出口位置进入隧洞;若不考虑压差作用,水流的拖曳作用将使空气向出口方向运动。该工况下洞内余幅较大,掺气水流的拖曳能力较为有限,仅能抵抗一部分压差作用,因而在拖曳作用下仅带走靠近掺气水体的部分空气,靠近洞顶位置的空气将在压差的作用下由隧洞出口进入洞内,形成一个大的气流循环,对应的气流循环示意图如图6所示。 图6 隧洞内气流循环示意图 基本的水气特征参数包括水流流速和掺气浓度,设定同一闸门开度,通过改变来流水头(对应单宽流量见表1)对掺气浓度、平均掺气浓度和水流流速等参数沿水流方向的变化规律进行了探究。 表1 闸门开度为40%时不同来流水头对应单宽流量 对于给定的闸门开度,当改变来流水头时各断面水流流速分布如图7所示。由图7可以看出,当闸门开度不变,来流水头逐渐增大时,水流流速的分布形式相似;当闸门开度一定,来流水深保持一致时随着来流水头的增加,来流流量逐渐增大,水流流速也随之增大。 图7 闸门开度为40%时不同来流水头He下各断面水流流速分布 保持闸门开度为40%时,不同来流水头各断面掺气浓度分布如图8所示。由图8可以看出,对于给定来流水头,距离闸门较近位置,掺气现象仅在靠近自由面一定深度内发生,空气还未贯穿至隧洞底部,因而底部还存在清水区。随着与闸门距离的增加,掺气现象进一步发生,掺入水体的空气逐渐到达隧洞底部,清水区逐渐消失。此外,掺气浓度分布曲线变化趋势更加平缓,相比靠近闸门位置分布更加均匀。当来流水头逐渐增大时,各断面处掺气浓度分布基本一致。对于某一断面位置而言,由于来流水头逐渐增大,来流流速增大,水-气紊动作用更加剧烈,掺气量增大,造成掺气水深增大,掺气浓度分布更加平缓。在x=1.00 m断面处,3种来流水头下隧洞底部附近均存在清水区,当来流水头增大时,自由面位置掺气区域深度越大,且掺气水深越大;在x=5.98 m断面处,隧洞底部附近清水区均已消失,随着来流水头增大,近底掺气浓度增大。 图8 闸门开度为40%时不同来流水头He下各断面掺气浓度分布 当闸门开度为40%时,不同来流水头近底掺气浓度沿程变化如图9所示。由图9可见,距离闸门较近的位置,掺入水体的空气量较少,未扩散至隧洞底部,因而近底掺气浓度均为零,随着与闸门距离的增大,空气在剧烈的紊动作用下扩散至隧洞底部,近底掺气浓度大于0。由出口位置近底掺气浓度可明显得到:随着来流水头He的逐渐增大,水-气紊动作用更加剧烈,造成出口位置近底掺气浓度由He=5 m时的0.006增大至He=15 m时的0.060。 图9 闸门开度为40%时不同来流水头He下近底掺气浓度沿程变化 掺气层厚度反映了空气对掺气水流的影响范围,将掺气层厚度定义为0.01 (12) 式中,haw为掺气层厚度,m;ZC=0.01为C=0.01时的水深,m;ZC=0.99为C=0.99时的水深,m。 闸门开度为40%时,不同来流水头掺气层厚度沿程变化如图10所示。图10中结果表明,对于不同来流水头,掺气层厚度变化趋势一致,即在距闸门较近位置处的掺气层厚度较小,随着与闸门距离的增大,掺气层厚度开始迅速增大,流动一段距离后,增加趋势变缓,趋于稳定状态。 图10 闸门开度为40%时不同来流水头He下掺气层厚度沿程变化 对于某一断面来说,随着来流水头的增大,水流流速增大,水-气之间的紊动作用更加剧烈,洞内空气更易于掺入水体中,造成水体掺气程度进一步加强,断面上掺气量随之增大,出口位置掺气层厚度由0.08 m增大至0.12 m。 数值模拟是目前研究掺气问题的重要方法,本文基于自主开发的NEWTANK数值模型,构建了混合-浓度数值模型用于研究水气二相流问题,通过有限差分方法进行离散并求解,并对洞内掺气水流进行了数值模拟研究,主要结论如下: (1)通过混合模型获得混合流场和压力场,紊流模型简化流场内的紊动发展过程,浓度模型用于追踪自由液面位置并获取掺气水流内部的掺气浓度分布信息。水流流速与掺气浓度的数值模拟结果和试验结果吻合良好,验证了该数值模型研究洞内掺气问题的可行性。 (2)距闸门较近位置,隧洞底部存在清水区,随着与闸门距离的增加,掺气进一步发生,空气贯穿至底部,清水区逐渐消失,掺气浓度分布曲线变化趋势更加平缓。当洞内余幅较大时,掺气水流的拖曳能力有限,仅能抵抗部分压差作用带走靠近掺气水体的空气,洞顶位置的空气将在压差作用下由隧洞出口位置进入洞内,形成一个大的气流循环,且洞内上方逆向气流速度沿水流方向由2 m/s增大至5 m/s。 (3)当闸门开度一定,来流水头由5 m增大至15 m时,水流流速分布相似,流速逐渐增大,水-气间紊动作用更加剧烈,洞内空气更易于掺入水体中,掺气程度进一步加强,造成靠近出口位置的近底掺气浓度由0.006增大至0.060,掺气层厚度由0.08 m增大至0.12 m。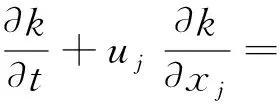

2.2 浓度模型
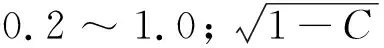
2.3 数值模型计算流程
3 模型设置与验证
3.1 模型设置

3.2 掺气浓度验证
3.3 水流流速验证
4 来流水头对水流流速和掺气浓度的影响

4.1 对水流流速的影响

4.2 对掺气浓度的影响
5 结 论
