空位对Hf-Ta-C体系的结构、力学性质及电子性质影响的第一性原理研究

2022-04-12彭军辉TIKHONOVEvgenii

无机材料学报 2022年1期

彭军辉, TIKHONOV Evgenii

彭军辉1,2, TIKHONOV Evgenii1

(1. 西北工业大学材料学院, 材料发现国际中心, 西安 710072; 2. 太原工业学院材料工程系, 太原 030008)

本研究理论预测了三元Hf-Ta-C空位有序结构以及空位对力学性质的影响。采用第一性原理进化晶体结构预测软件USPEX, 预测得到了5种热力学稳定和3种亚稳的(Hf, Ta)C1–x空位有序结构, 这些结构都属于岩盐结构。采用第一性原理方法, 计算了(Hf, Ta)C1–x空位有序结构的力学性质, 并分析了力学性质随空位浓度的变化。(Hf, Ta)C1–x都具有较高的体模量、剪切模量、杨氏模量和维氏硬度；各(Hf, Ta)C1–x的Hf/Ta比相同时, 其模量、硬度等随空位浓度增大而减小。最后, 计算了(Hf, Ta)C1–x的电子态密度, 发现其均具有强共价性和弱金属性。本研究结果对于了解Hf-Ta-C体系的空位结构及其力学性质和应用, 具有重要参考价值。

Hf-Ta-C体系; 空位有序结构; 维氏硬度; 第一性原理方法

现代航空航天工业面临的一个重要问题是, 开发使用温度超过3300 K的耐高温材料[1]。在超高温陶瓷体系中, 碳化铪和碳化钽是已知熔点最高的二元化合物, 熔点均超过4000 K (TaC的熔点为4041～4256 K[2-4], HfC为4023～4232 K[2-4])。此外, 碳化铪和碳化钽具有高杨氏模量、高硬度和物理化学性能稳定等优良的综合性能, 是航空航天领域的热门候选材料[5-6]。常温常压下, HfC和TaC具有岩盐结构, 可形成具有更高熔点、杨氏模量和硬度的三元固溶体[2,7-9]。因此, 三元Hf-Ta-C化合物也受到了广泛关注[2-4,7-15]。

Andrievskii等[2]测量发现HfTa4C5的熔点最高, 达到4263 K。Smith等[7]采用理论和实验结合的方法, 研究了HfC-TaC体系的结构、杨氏模量、维氏硬度和滑移性能, 发现Hf3TaC4的硬度和杨氏模量最大。采用第一性原理方法, Peng等[8]预测了HfC-TaC体系的结构和力学性质等, 发现HfTa2C3具有最高的剪切模量和杨氏模量。Zhang等[9]采用热压法制备了Hf4TaC5、Hf3TaC4、HfTaC2、HfTa4C5等, 在2373 K和70 MPa条件下得到了均匀的单相, 相对密度大于95%。由于固溶强化作用, HfC-TaC固溶体的硬度>30 GPa, 明显比二元化合物高。目前, 国内外对三元Hf-Ta-C体系的研究, 主要集中在HfC-TaC固溶体特别是HfTa4C5的制备、表征和熔点测量上[2-4,7-15]。

但正如Gusev等[16]研究发现, 过渡金属碳化物、氮化物及碳氮化合物均是强非化学计量比化合物, 在低温和退火条件下, 会形成空位有序化合物；除化学组成外, 其性能还受到空位浓度和有序度的影响。Gusev等[16]总结了二元过渡金属碳化物和氮化物的有序结构, 以及有序性对力学、热学、电学等性能的影响。Holleck[17]研究了二元过渡金属碳化物和氮化物的硬度随空位浓度的变化, 空位浓度大约为0.15时, TaC的微观硬度最大, 而HfC的微观硬度随空位浓度增大而减小。Rudy[3]分别测量了Hf-C体系和Ta-C体系的熔点, 发现HfC0.97和TaC0.94的熔点最高。Zeng等[18]采用从头算变成分进化结构预测方法, 搜索了Hf-C体系的有序结构, 除HfC外, 还发现空位有序结构Hf3C2和Hf6C5, 且均为岩盐结构, 同时研究了空位对力学性质和电子性质的影响。Yu等[19]预测了Ta-C体系的热力学稳定结构和亚稳结构, 发现了两类结构: 岩盐结构和Ta2C型结构。

但是目前还没有三元Hf-Ta-C空位有序结构的报道。Rudy[3]总结了Hf-Ta-C体系在高温下(1273 K以上)的相图, 发现存在两类三元无序固溶体结构–岩盐结构和Ta2C型固溶体, 但没有发现三元空位有序结构。鉴于此, 本研究基于第一性原理进化算法, 对Hf-Ta-C体系的三元空位有序结构进行了搜索, 发现了8种热力学稳定或亚稳结构, 且都满足力学稳定性和晶格动力学稳定性。继而研究了空位对力学性能等的影响, 为该类材料的实验研究和工程应用等提供了理论依据。

1 计算方法

本研究基于第一性原理进化算法, 采用USPEX软件[20-22]搜索(Hf, Ta)C1–x的空位有序结构,包括HfTa2C2、HfTa3C3、HfTa5C5、Hf2TaC2、Hf2Ta2C3、Hf2Ta4C5、Hf2Ta6C7、Hf3TaC3、Hf3Ta3C5、Hf4Ta2C5、Hf5TaC5、Hf6Ta2C7等共12种组分的结构, 单胞中原子数不超过20个。初始结构(60个原子)由USPEX[20-22]随机产生, 从第二代开始, 每代结构(总共50个原子)分别由遗传(40%)、软模变异(20%)、晶格变异(10%)、原子位置交换(10%)、随机(20%)等进化操作产生。对USPEX[20-22]产生的每个结构, 采用第一性原理VASP软件[23]计算其能量, 筛选出每种组分下能量最低的结构。当连续20代最稳定结构相同时, 或搜索完成30代结构时, 计算停止。

对(Hf, Ta)C1–x各组分下能量最低的结构, 提高计算精度, 采用VASP软件[23]进行结构优化和性质计算。结构优化时, 采用PAW方法[24], 截断能为600 eV, 交换关联能采用GGA-PBE赝势[25], 布里渊区高对称点间距为2π×0.18 nm–1, 能量收敛判据为: 能量差10–8eV/atom, 压力为10–2eV/nm。然后, 采用有限位移法计算(Hf, Ta)C1–x的弹性常数, 采用Phonopy软件[26]计算(Hf, Ta)C1–x的声子谱曲线, 采用VESTA软件[27]画出其晶体结构和模拟X射线衍射图谱。

2 结果与讨论

2.1 晶体结构预测及(Hf, Ta)C1–x空位有序结构

采用进化晶体结构预测软件USPEX[20-22], 搜索了常压下Hf-Ta-C体系的三元空位有序结构。图1(a)为Hf-Ta-C体系的能量凸包图, (Hf, Ta)C1–x形成焓的计算公式如下:

Δf={[(Hf1–yTa)C1–x]–[(1–)(Hf)+

(Ta)+(1–)(C)]}/(2–) (1)

如图1(a)所示, 除了已报道的不含空位的Hf1–xTaC外[8], 还发现了5种热力学稳定和3种亚稳的空位有序化合物及其结构。这些结构的化学组成、空间群、晶格常数、高于凸包线的能量、空位浓度等, 如表1所示。对于这3种亚稳结构, 其高出凸包线的能量大约在0.001 eV/atom, 非常接近凸包线, 可以看作是近似稳定结构。实验中发现的高温(Hf, Ta)C1–x均为无序结构[3], 目前还没有空位有序结构的报道, 因此这些结构均为首次发现。

图1(b)是(Hf, Ta)C1–x空位有序结构的模拟X射线衍射图谱, (Hf, Ta)C1–x的衍射峰形状与HfC、TaC相似, 衍射角位于两者之间, 证明其结构与HfC和TaC类似, 即具有岩盐结构。

除了满足热力学稳定性或亚稳性外, 如表2和图2所示, (Hf, Ta)C1–x空位有序结构同时满足力学稳定性[28]和晶格动力学稳定性条件。

图3为(Hf, Ta)C1–x空位有序结构的某一晶面图, Hf、Ta原子形成[Hf6–xTa]八面体, 碳原子和空位有序地分布在八面体间隙。由于空位取代了C原子的位置, Hf或Ta原子的配位数小于6(表1)。空位浓度小于或等于1/6时, 具有3阶及以上最近邻空位对; 空位浓度大于或等于1/4时, 存在1阶最近邻空位对,但不存在2阶最近邻空位对。

2.2 (Hf, Ta)C1–x空位有序结构的力学性质

本研究采用VASP软件[23]计算(Hf, Ta)C1–x空位有序结构的弹性常数, 如表2所示。根据计算的弹性常数, 基于Hill近似[29], 得到体模量()、剪切模量()、杨氏模量()、泊松比()。采用Chen模型[30]计算了维氏硬度(V), 计算公式如下:

V= 2(2)0.585–3 (2)

其中, Pugh比[31]=/。表2为(Hf, Ta)C1–x空位有序结构的弹性常数和力学性质, 可以看到这些空位有序结构都具有非常高的模量和硬度。

图1 晶体结构预测及(Hf,Ta)C1–x空位有序结构

(a) Enthalpy convex-hull of ternary Hf-Ta-C system (black sphereindicating stable structure, while others indicating metastable structure,and red square representing the structure with high enthalpy above the convex-hull, but not considered here); (b) Simulated X-ray diffractions of (Hf, Ta)C1–xvacancy ordered structures with a copperKX-ray source

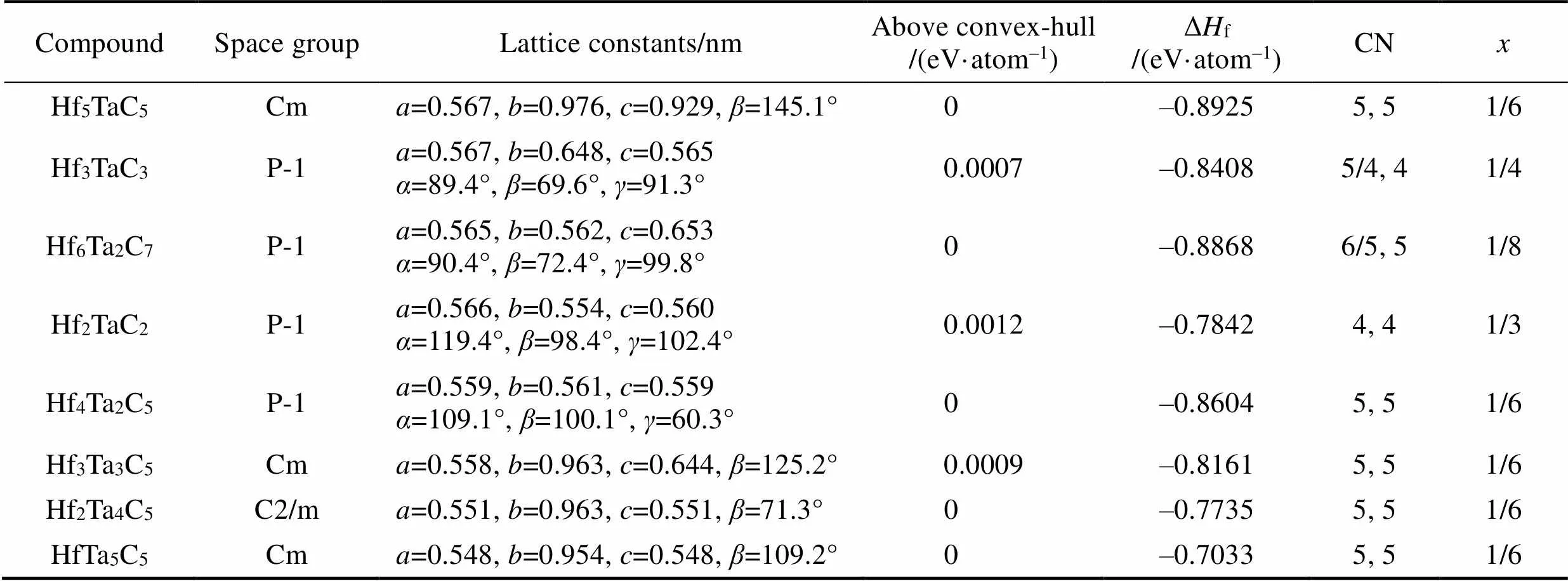
表1 (Hf, Ta)C1–x空位有序结构的空间群、晶格常数、高于凸包线的焓值、形成焓(ΔHf)、原子配位数(CN)、空位浓度(x)

*CN: coordination number of Hf or Ta;: the concentration of vacancy

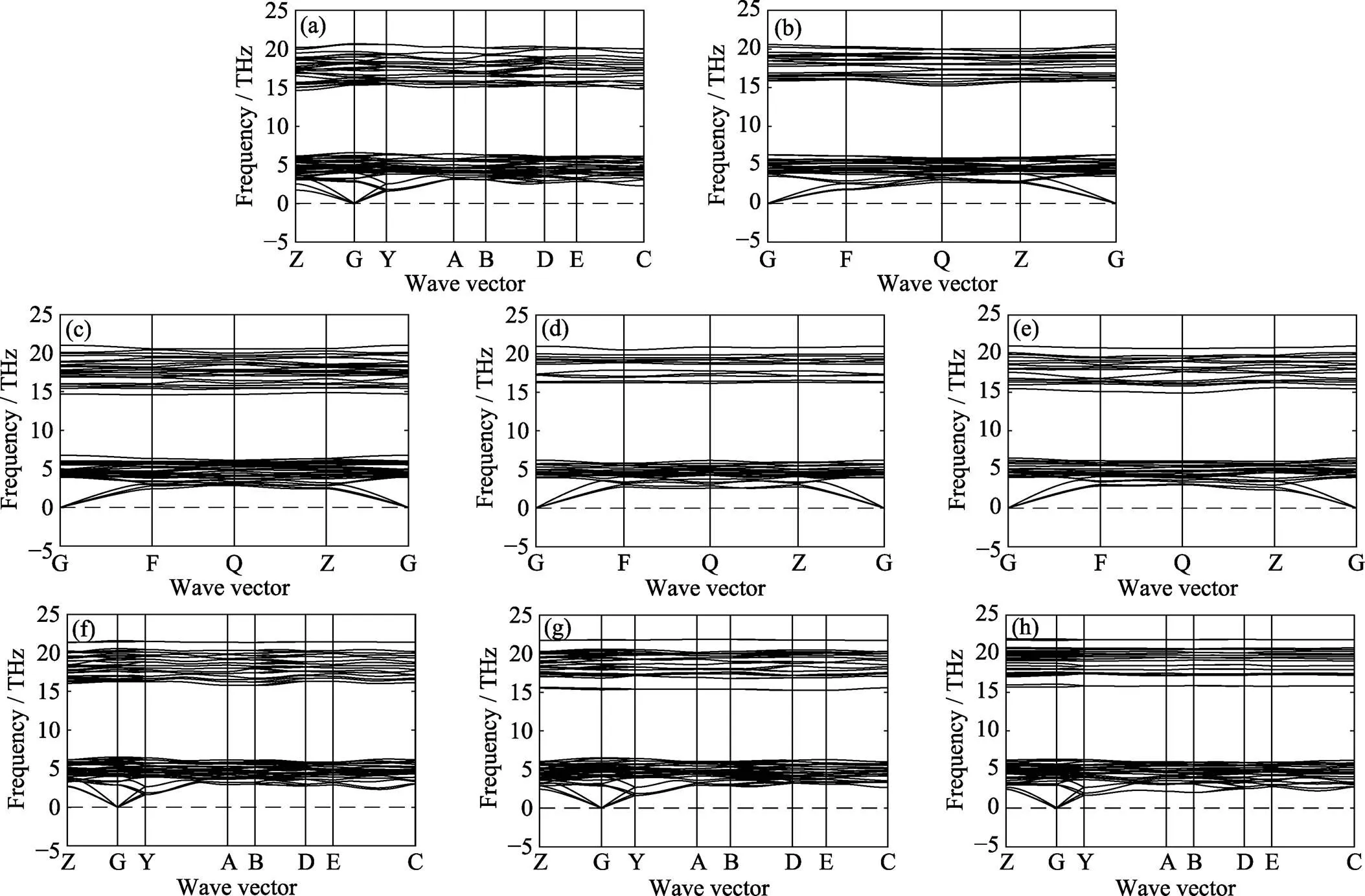
图2 (a) Hf5TaC5、(b) Hf3TaC3、(c) Hf6Ta2C7、(d) Hf2TaC2、(e) Hf4Ta2C5、(f) Hf3Ta3C5、 (g) Hf2Ta4C5和(h) HfTa5C5的声子谱曲线

They are all dynamical stable because no imaginary frequencies were found in Brillouin zone

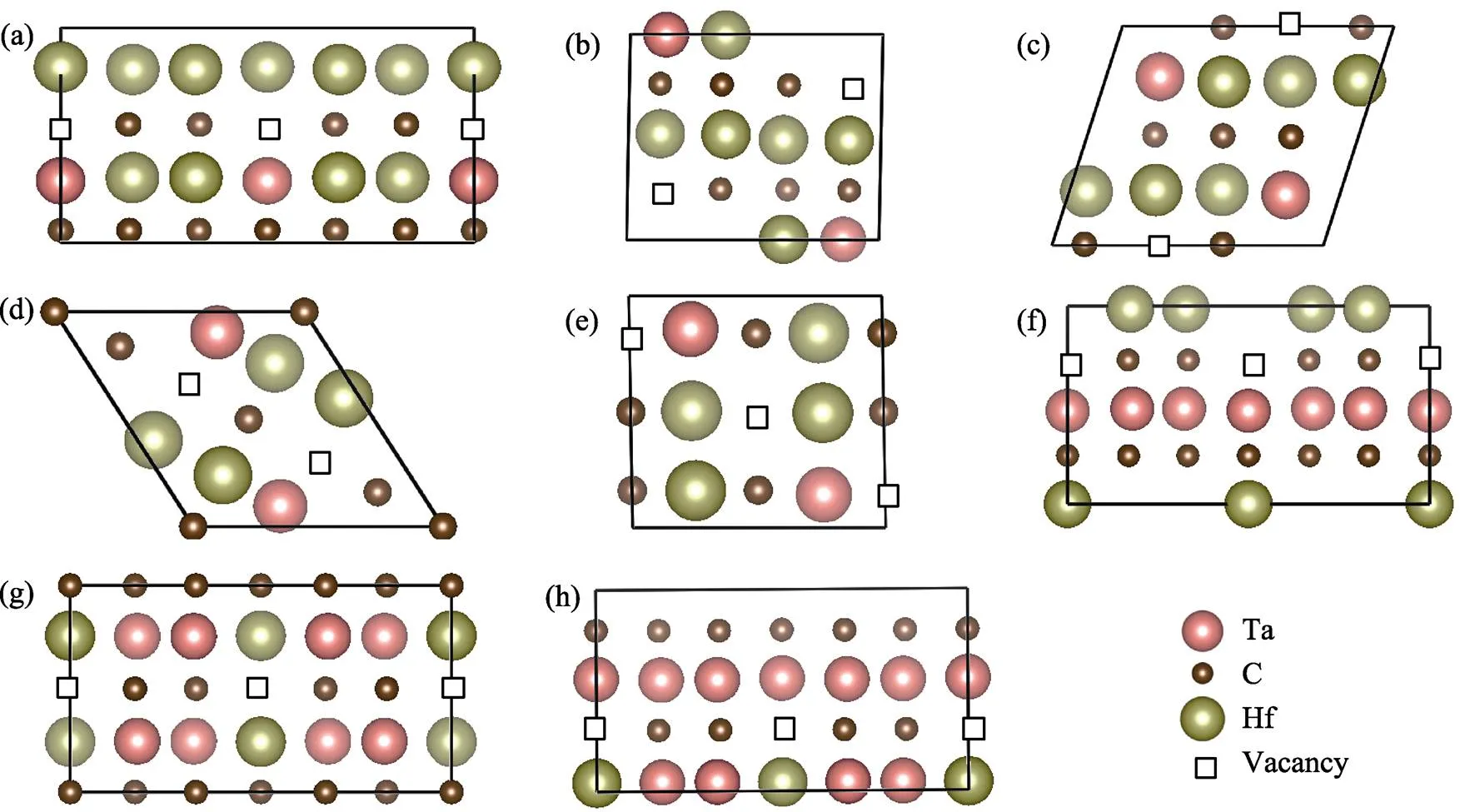
图3 (a) Hf5TaC5、(b) Hf3TaC3、(c) Hf6Ta2C7、(d) Hf2TaC2、(e) Hf4Ta2C5、(f) Hf3Ta3C5、 (g) Hf2Ta4C5和(h) HfTa5C5的晶体结构

图4为(Hf, Ta)C1–x空位有序结构的力学性质随空位浓度变化的关系, 其中文献[8]已报道Hf1–xTaC的力学性质。相同Hf/Ta比例下, (Hf, Ta)C1–x的、、、V、/等随空位浓度的增大而降低, 而泊松比随之增大。这是由于空位抵抗外力的能力很弱, 空位比例越高, 模量和硬度越小。

表2 (Hf, Ta)C1–x空位有序结构的弹性常数(Cij)、体模量(B)、剪切模量(G)、杨氏模量(E)、泊松比(μ)、维氏硬度(Hv)和Pugh比(G/B)

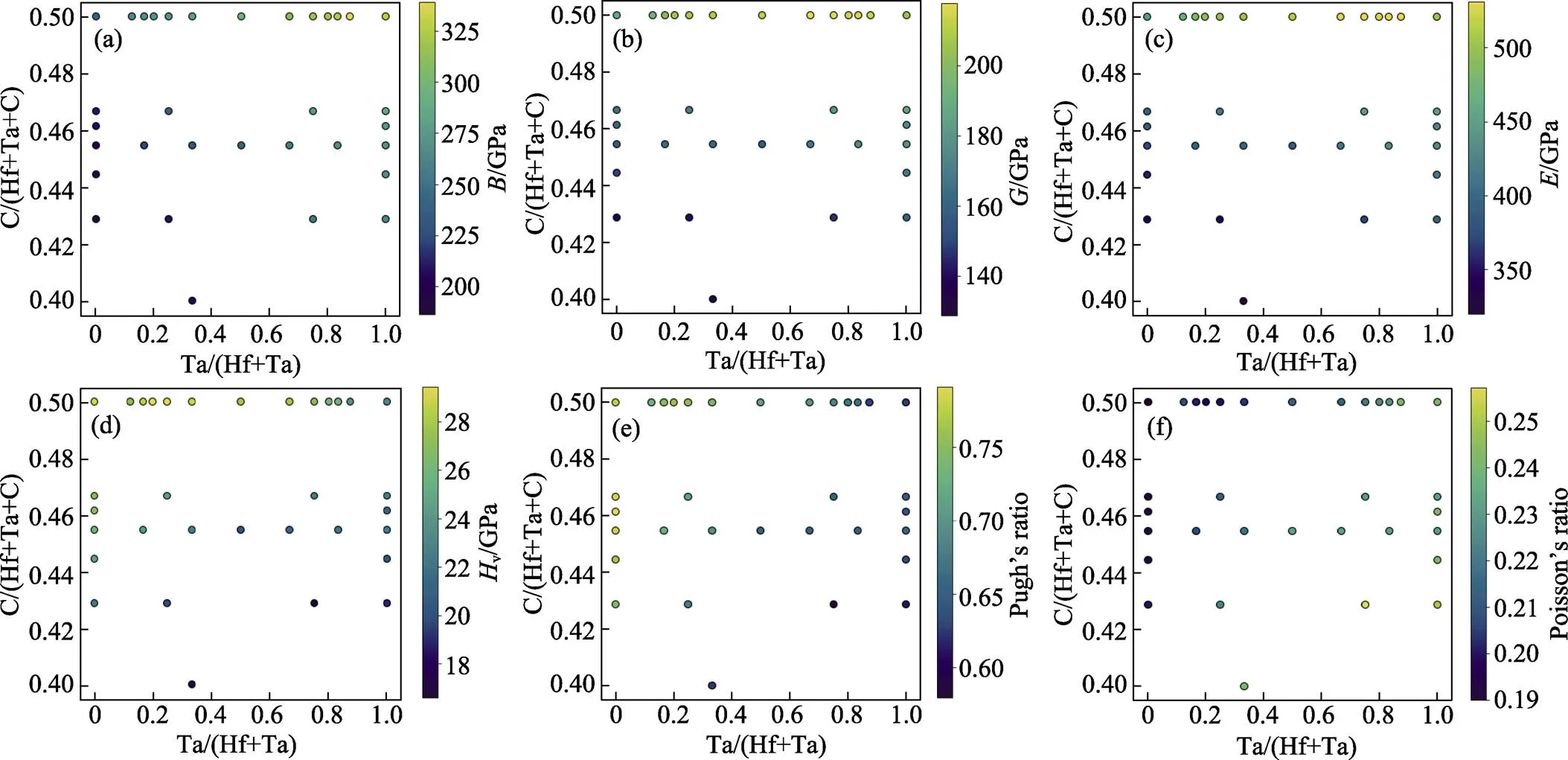
图4 空位对Hf-Ta-C体系力学性质的影响

(a) Bulk modulus (); (b) Shear modulus (); (c) Elastic modulus (); (d) Vickers hardness (V); (e) Pugh’s ratio (/); (f) Poisson’s ratio ()

2.3 (Hf, Ta)C1–x空位有序结构的电子性质

为了研究化学键特点, 本研究计算了(Hf, Ta)C1–x空位有序结构的电子态密度和分态密度(图5)。在–5～–2 eV范围内, Hf-d或Ta-d轨道与C-p轨道存在很强的杂化作用, 即Hf–C和Ta–C键具有非常强的共价特性。这是(Hf, Ta)C1–x具有非常高的模量和硬度的原因。且在Fermi面处, 存在少量自由电子, 即具有弱的金属性。则(Hf, Ta)C1–x空位有序结构的化学键具有强共价性和弱金属性, 这一特点与二元过渡金属碳化物相同[18-19]。

Razumovskiy等[32]和Zhang等[33]研究发现, 二元过渡金属碳化物、氮化物空位有序结构中, 除二阶最近邻空位对外, 其它有序分布空位的相互作用能量都比较低, 使其能够稳定存在。对于具有相同结构类型的(Hf, Ta)C1–x结构(图3), 不存在二阶最近邻空位对, 因而形成焓很低(表1), 且其焓值位于或非常接近凸包线; 即(Hf, Ta)C1–x空位有序结构能够稳定存在。如图5所示, 尽管存在一定浓度的空位, (Hf, Ta)C1–x空位有序结构中Hf-C和Ta-C间仍存在强的共价键作用。因此, 不管从能量还是结合角度, (Hf, Ta)C1–x都能够形成稳定的空位有序结构。

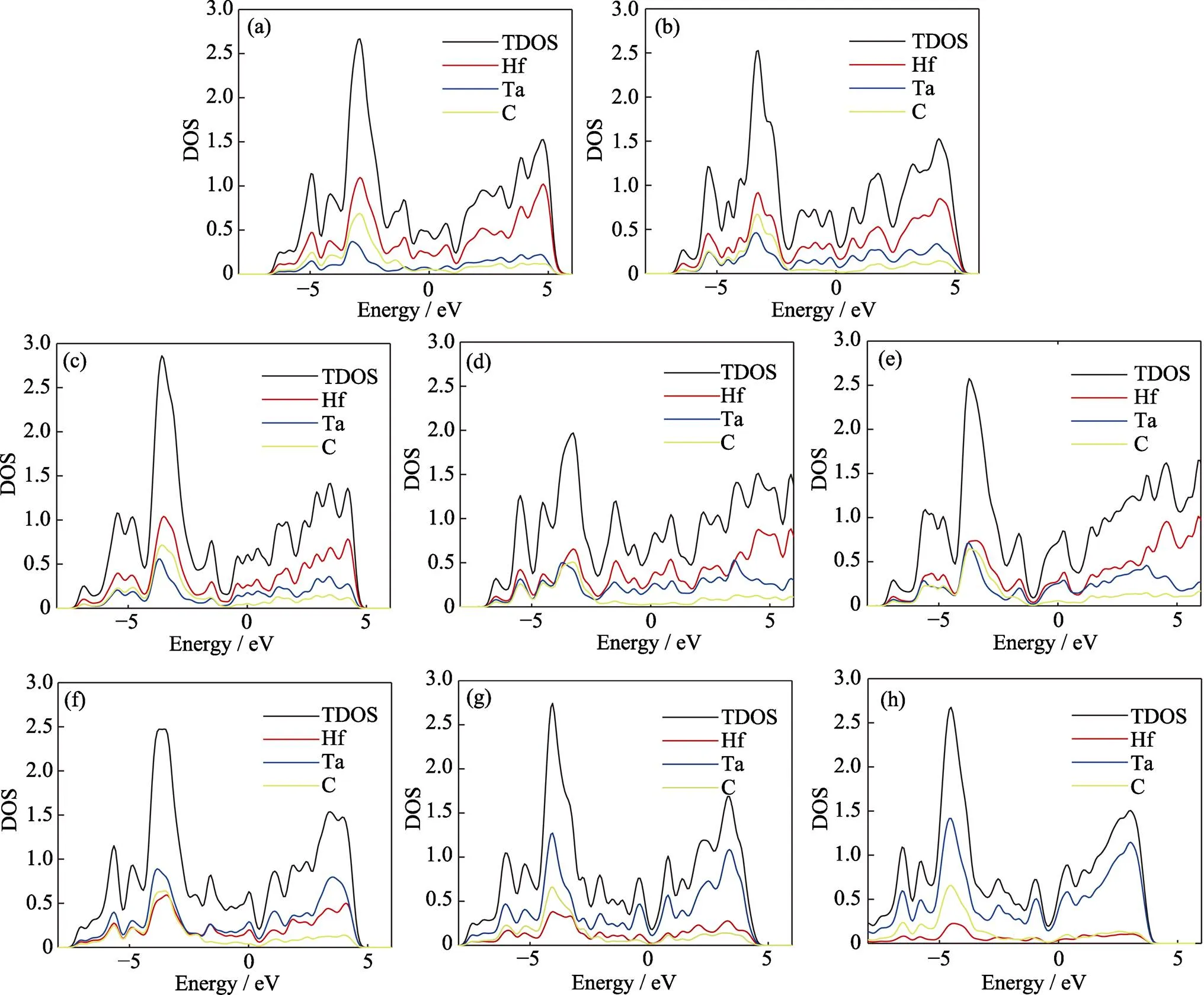
图5 (a) Hf5TaC5、(b) Hf3TaC3、(c) Hf6Ta2C7、(d) Hf2TaC2、(e) Hf4Ta2C5、(f) Hf3Ta3C5、 (g) Hf2Ta4C5和(h) HfTa5C5的态密度和分态密度(Fermi能级位于0 eV)

DOS is density of state / (states/eV); TDOS is total DOS; Hf, Ta, C are PDOS of Hf atom, Ta atom and C atom, respectively

Colorful figures are available on the website

3 结论

本研究发现了5种稳定和3种亚稳的(Hf, Ta)C1–x空位有序结构; 这3种亚稳结构的能量非常接近凸包线, 可以看作近似稳定结构。(Hf, Ta)C1–x空位有序结构均属于岩盐结构类型。(Hf, Ta)C1–x具有高体模量、剪切模量、杨氏模量和维氏硬度; 相同Hf/Ta比下, (Hf, Ta)C1–x的模量、硬度等随着空位浓度增大而减小。(Hf, Ta)C1–x的化学键具有强共价性和弱金属性, 这一特点与二元碳化物相同。(Hf, Ta)C1–x具有较低的形成焓和强的结合, 因此能够形成稳定的空位有序结构。

[1] KURBATKINA V V, PATSERA E I, LEVASHOV E A,. Self-propagating high-temperature synthesis of single-phase binary tantalum-hafnium carbide (Ta, Hf)C and its consolidation by hot pressing and spark plasma sintering., 2018, 44(4): 4320–4329.

[2] ANDRIEVSKII R A, STRELNIKOVA N S, POLTORATSKII N I,. Melting point in systems ZrC-HfC, TaC-ZrC, TaC-HfC., 1967, 6: 65–67.

[3] RUDY E. Ternary phase equilibria in transition metal-boron- carbon-silicon systems. Part II. Ternary systems, Vol. I. Air Force Materials Laboratory: Wright-Patterson Air Force Base, 1965: 35–73.

[4] CEDILLOS-BARRAZA O, MANARA D, BOBORIDIS K,. Investigating the highest melting temperature materials: a laser melting study of the TaC-HfC system., 2016, 6: 37962.

[5] ZHANG X H, HILMAS G E, FAHRENHOLTZ W G,. Hot pressing of tantalum carbide with and without sintering additives., 2007, 90(2): 393–401.

[6] CEDILLOS-BARRAZA O, GRASSO S, NASIRI N A,. Sintering behaviour, solid solution formation and characterisation of TaC, HfC and TaC-HfC fabricated by spark plasma sintering., 2016, 36(7): 1539–1548.

[7] SMITH C J, YU X X, GUO Q,. Phase, hardness, and deformation slip behavior in mixed HfTa1–xC., 2018, 145: 142–153.

[8] PENG J, TIKHONOV E. Improving the mechanical properties of HfC-based ceramics by exploring composition space of Hf1–xTaC and HfC1–xN., 2021, 195: 110464.

[9] ZHANG J, WANG S, LI W. Consolidation and characterization of highly dense single-phase Ta-Hf-C solid solution ceramics., 2019, 102: 58–62.

[10] GABALLA O, COOK B A, RUSSELL A M. Reduced-temperature processing and consolidation of ultra-refractory Ta4HfC5.,2013, 41: 293–299.

[11] GHAFFARI S A, FAGHIHI-SANI M A, GOLESTANI-FARD F,. Spark plasma sintering of TaC-HfC UHTCdisilicides sintering aids., 2013, 33(8): 1479–1484.

[12] PABLO G, LUIS Y, MERCY S,. Characterization of the micro-abrasive wear in coatings of TaC-HfC/Au for biomedical implants., 2017, 10(8): 842.

[13] ZHANG C, GUPTA A, SEAL S,. Solid solution synthesis of tantalum carbide-hafnium carbide by spark plasma sintering., 2017, 100: 1853–1862.

[14] FOROUGHI P, ZHANG C, AGARWAL A,. Controlling phase separation of TaHf1–xC solid solution nanopowders during carbothermal reduction synthesis., 2017, 100: 5056–5065.

[15] KIM J, KWON H, KIM B,. Finite temperature thermal expansion and elastic properties of (Hf1–xTa)C ultrahigh temperature ceramics., 2019, 45: 10805–10809.

[16] GUSEV A I, REMPEL A A, MAGERL A J. Disorder and order in strongly nonstoichiometric compounds. Berlin Heidelberg: Springer, 2001: 179–243.

[17] HOLLECK H. Material selection for hard coatings., 1986, 4(6): 2661–2669.

[18] ZENG Q, PENG J, OGANOV A R,. Prediction of stable hafnium carbides: stoichiometries, mechanical properties, and electronic structure., 2013, 88: 214107.

[19] YU X X, WEINBERGER C R, THOMPSON G B.investigations of the phase stability in tantalum carbides., 2014, 80: 341–349.

[20] OGANOV A R, GLASS C W. Crystal structure prediction usingevolutionary techniques: principles and applications., 2006, 124(24): 244704.

[21] LYAKHOV A O, OGANOV A R, STOKES H T,. New developments in evolutionary structure prediction algorithm USPEX., 2013, 184: 1172–1182.

[22] OGANOV A R, LYAKHOV A O, VALLE M. How evolutionary crystal structure prediction works and why., 2011, 44(3): 227–237.

[23] KRESSE G, FURTHMULLER J. Efficient iterative schemes fortotal-energy calculations using a plane-wave basis set., 1996, 54(16): 11169–11186.

[24] BLOCHL P E. Projector augmented-wave method., 1994, 50(24): 17953–17979.

[25] PERDEW J P, RUZSINSZKY A, CSONKA G I,. Restoring the density-gradient expansion for exchange in solids and surfaces., 2008, 100(13): 136406.

[26] TOGO A, OBA F, TANAKA I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2at high pressures., 2008, 78: 134106.

[27] MOMMA K, IZUMI F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data., 2011, 44: 1272–1276.

[28] COWLEY R A. Acoustic phonon instabilities and structural phase transitions., 1976, 13(11): 4877–4885.

[29] HILL R. The elastic behavior of a crystalline aggregate., 1952, 65(5): 349–354.

[30] CHEN X Q, NIU H, LI D,. Modeling hardness of polycrystalline materials and bulk metallic glasses., 2011, 19(9): 1275–1281.

[31] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals., 1954, 45(367): 823–843.

[32] RAZUMOVSKIY V I, POPOV M N, DING H,. Formation and interaction of point defects in group IVb transition metal carbides and nitrides., 2015, 104: 147–154.

[33] ZHANG Y, LIU B, WANG J. Self-assembly of carbon vacancies in sub-stoichiometric ZrC1–x., 2015, 5: 18098.

Vacancy on Structures, Mechanical and Electronic Properties of Ternary Hf-Ta-C System: a First-principles Study

PENG Junhui1,2, TIKHONOV Evgenii1

(1. International Center for Materials Discovery, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China; 2. Department of Materials Engineering, Taiyuan Institute of Technology, Taiyuan 030008, China)

In this study, the first-principles method was used to predict the vacancy ordered structures of ternary Hf-Ta-C system and the effect of vacancy on its mechanical properties.Crystal structure of (Hf, Ta)C1–xunder ambient pressure were predicted by first-principles evolutionary using USPEX software. This calculation found 5 stable and 3 metastable vacancy ordered structures which all share the rock-salt structure. Then, mechanical properties of (Hf, Ta)C1–xvacancy ordered structures were calculated by the first-principles method, and change of mechanical properties with the concentration of vacancy was analyzed. They all showed high bulk modulus, shear modulus, elastic modulus, and Vickers hardness. Their moduli and hardness decreased with the increase of the concentration of vacancy at the same Hf/Ta ratio. Finally,their electronic density of states are calculated, revealing that their chemical bonding is a mixture of strong covalence and weak metallic. Data from this study are promising for understanding vacancy ordered structures, mechanical properties and applications of Hf-Ta-C system.

Hf-Ta-C system; vacancy ordered structure; Vickers hardness; first-principles method

1000-324X(2022)01-0051-07

10.15541/jim20210179

O411

2021-03-20;

2021-04-30;

2021-06-10

外国人才引进与学术交流项目(B08040)

Foreign Talents Introduction and Academic Exchange Program of China (B08040)

彭军辉(1989–), 男, 博士研究生. E-mail: pjh1989@yeah.net

PENG Junhui(1989–), male, PhD candidate. E-mail: pjh1989@yeah.net

TIKHONOV Evgenii, 助理教授. E-mail: tikhonov.e@nwpu.edu.cn