教与学信息交互粒子群优化算法

聂方鑫，王宇嘉，贾欣

（上海工程技术大学电子电气工程学院，上海 201620）

0 引言

粒子群优化（Particle Swarm Optimization，PSO）算法［1］于1995 年由Kennedy 与Eberhart 提出，该算法以群体智能作为基础，采用没有体积、没有质量的粒子作为个体，并规定每个粒子的行为方式，使得整个种群呈现出复杂的特征以求解优化问题。PSO 算法因其简单性和强大的收缩能力被广泛用于不同领域，并得到了极为迅速的发展和推广。虽然PSO 算法在很多方面有着不错的表现，但其具有易陷入局部最优和优化后期收敛慢的缺陷。为了解决上述问题，研究者提出了各种方法来提高粒子群算法的搜索效率［2-4］，主要分为两类：

第一类，与其他优化算法相结合。例如，文献［5］中提出了一种改进型粒子群算法，将PSO 算法、遗传算法和模拟退火算法三者相融合，增强了算法的收敛能力，同时也抑制了算法“早熟”；文献［6］中将量子行为粒子群和人工蜂群算法相结合来辨识模型参数，对于有噪声的数据，双种群算法表现最好；文献［7］中将人类学习优化算法与PSO 算法相融合，在人类学习优化算法指导下，增强粒子学习能力，提高PSO搜索效率；文献［8］中提出了一种新的粒子群与混合蛙跳融合算法，采用多种群方法，在每次进化后，将各子群中最优粒子组成新的群体，并采用混合蛙跳模式进行进化，以提高种群多样性；文献［9］中提出了一种融合Rosenbrock 搜索法的混合粒子群算法，利用Tent 混沌序列将种群初始化，接着对个体极值进行扰动，增强了种群多样性，并利用Rosenbrock搜索法对全局最优个体进行局部搜索，最终提高了解的精度。上述研究都是将算法进行融合改进，在一定程度上提高了PSO 算法的性能，但并没有从根本上解决PSO 算法收敛能力和多样性之间的冲突。

第二类，研究各种改进PSO 算法。例如，文献［10］中提出了一种具有重组学习和混合变异的动态多种群粒子群优化算法，动态地划分了多个子种群，并融入重构粒子作为引导因子，同时对最优个体实施混合变异、反向学习策略和邻域扰动操作，帮助粒子快速跳出局部最优；文献［11］中提出了一种快速多种群粒子群多模优化算法，采用动态半径和种群划分策略，同时引入拓扑机制，使种群在快速收敛和多样性之间达到了平衡；文献［12］中提出了一种多种群综合学习算法，引入多种群策略以提高全局勘探能力，并采用全局学习策略更新学习样本，增加了种群多样性；文献［13］中提出了一种基于多种群的自适应迁移PSO 算法，将两种常用邻居拓扑结构进行融合，同时使多个子种群并行进化，利用不同的加速因子组合赋予了各子种群不同的搜索特性，最终提升了算法综合性能。上述研究都是对种群划分策略进行了改进，分群策略虽然能改善其性能，但是子种群间的交流也影响着算法收敛能力和种群多样性，并且粒子学习模式固定，对算法性能的提升有限。

本文提出一种教与学信息交互粒子群优化（Teaching and Learning information interactive PSO，TLPSO）算法，该算法根据进化过程将种群动态地划分为两个子种群，分别使用PSO 算法和教与学优化（Teaching-Learning-Based Optimization，TLBO）算法［14］进行迭代，利用教与学优化算法中学习者阶段进行信息交互，发挥优势种群长处，提升个体成绩，同时分别计算个体适应度值和个体间距离，采用指标加权策略，使粒子收敛性和多样性得到平衡，防止陷入局部最优。

1 基本理论

1.1 粒子群优化算法

在粒子群优化算法中，每个优化问题的潜在解都是搜索空间中的一个“粒子”，所有粒子都有一个速度来决定它们飞行方向和距离，粒子通过追寻当前最优粒子，在解空间中进行搜索。在每一次迭代中，粒子在追寻全局极值的同时，也追寻个体极值来更新自己位置。设在一个D维空间中，由m个粒子组成的种群X=(x1，x2，…，xi，…，xm)，其中，第i粒子位置为xi=(xi1，xi2，…，xiD)，其速度为vi=(vi1，vi2，…，viD)。个体 极值 为pi=(pi1，pi2，…，piD)，全局极值 为pg=(pg1，pg2，…，pgD)［15］。粒子xi的速度和位置更新公式为：

其中：ω表示权重系数；vid(t)和xid(t)分别表示粒子i在第d维第t次迭代中的速度和位置大小；c1和c2是加速因子；r1，r2和r3是分布在［0，1］内的随机数；pid和pgd分别表示粒子最优位置和群体最优位置。

1.2 教与学优化算法

教与学优化算法由Rao 等［14］提出，它模拟了班级中教师的教学行为和一些学习者的学习行为，教师和学习者等同于进化算法中的个体。在TLBO 算法中，将种群中所有个体集合称之为班级，班级中某个点xi=(xi1，xi2，…，xiD)称之为一个个体，D为优化问题的维数，当前适应值最好的个体称之为教师，用xteacher表示。该算法分为两个阶段，分别为教学阶段和学习阶段，这两个阶段的目标都是为了提高每个个体的成绩［16］。

在教学阶段，每个个体向群体中最好的个体xteacher学习，以提高自己的成绩。考虑到教师的教学成果也受平均成绩的影响，因此个体在教学阶段的更新公式为：

其中：xold，i和xnew，i分别是第i个个体学习前和学习后的个体；学习因子ri=rand(0，1)；教学因子TF=round[1 +rand(0，1)]；xmean是整个种群适应度值均值。如果xnew，i的适应度值优于xold，i，就更新xold，i，否则不更新。

在学习阶段，每个个体也通过与其他个体进行交流，来提高自己的成绩。具体来说，个体xi随机选择另一个个体xj进行交流学习。

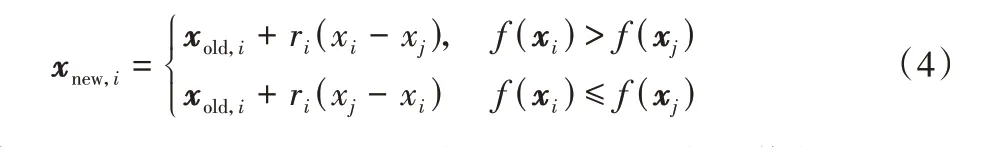
其中：学习因子ri=U(0，1)；如果xnew，i的适应度值优于xold，i，则更新个体，否则不更新。

2 教与学信息交互粒子群优化算法

2.1 种群动态调整方案

为了提高算法全局搜索能力，本文采用种群动态调整方案来增加种群多样性。首先根据式（5）和式（6）将种群动态划分为PSO 种群（P 群）和TLBO 种群（T 群），如图1（a）所示。

其中：NP和NT分别是P 群和T 群种群规模；NP是整个种群规模；a1～a4是影响因子，a1和a4是调整P 群最终占比和初始占比的影响因子，a1越大说明算法后期T 群所占比例越大，a4越大说明算法初期P 群所占比例越大，a2和a3调整P 群增长速度，a2和a3越大说明P 群增长速度越快；iter是当前迭代次数；MaxIt是最大迭代次数。

在算法迭代初期，P 群中粒子采用PSO 算法进化；而在T群中，从中挑选出NT1个粒子组成A 组，只采用TLBO 算法中学习阶段进行进化；剩下的粒子组成B 组，采用完整TLBO 算法进化，如图1（b）所示。因为在P 群和T 群B 组中粒子会向全局极值学习，导致多样性逐渐丧失，使算法陷入局部最优；而在T 群A 组中的粒子向除自己之外任何粒子学习，相对于使用PSO 算法，可有效地提高全局搜索能力［17］。

在算法迭代中期，P 群种群规模比T 群小。随着迭代次数增加，P 群种群规模逐渐变大，T 群种群规模逐渐变小，如图1（c）所示。在T 群A 组中处于TLBO 算法学习阶段的粒子具有良好的全局搜索能力，因此在调整子种群规模时，将这些粒子分配给P 群，但是在T 群中进化的粒子缺失速度这一参数，受PSO 算法位置更新策略启发，由式（7）求出P 群中被分配来的粒子速度：

在算法迭代后期，T 群A 组中粒子都已经分配给P 群，如图1（d）所示。此时由于在P 群和T 群B 组中粒子会向全局极值学习，所以可以使粒子在极值点附近进行更精细的局部搜索，提高收敛速度。

图1 子种群规模随迭代次数变化的动态过程Fig.1 Dynamic process of subpopulation size changing with number of iterations

由上面描述可知，这两个种群规模大小会影响算法全局探索和局部开发。因此，本文采用动态调整方案来控制进化过程中两个种群规模，使所提算法在进化前期可以保证种群多样性，提高全局搜索能力，进化后期可以提高收敛速度。

考虑到在整个种群进化过程中全局最优位置对个体运动的影响［18］，本文对PSO 算法中个体速度更新公式如式（8）所示：

其中：pp，gd是P 群全局最优位置；pgd是整个种群的全局最优位置；b1和b2是影响因子，使c3从0.5 线性增长到1.5。

2.2 种群信息交互

将整个种群动态划分为两个子种群后，子种群之间信息交互也影响着算法的效果，因此采用了两阶段学习策略使粒子互相交流学习。

在第一阶段，如图2 右下角所示：T 群内部A 组和B 组进行交流学习。首先比较两个小组适应度值大小，拥有最小适应度值小组称之为优秀小组，另一个小组为普通小组。然后从优秀小组中随机挑选一个学习粒子xl，普通小组中所有粒子使用TLBO 算法学习阶段的规则向学习粒子xl学习，并产生新后代。在T 群内部学习后，可以使T 群保持良好的全局探索能力，同时采用分组措施，可以防止因为粒子被分配到P 群而导致的信息流失，并且在算法后期阶段，还可以提升整个种群收敛速度，其更新公式为：

其中：xo，old，i和xo，new，i分别是A 组或者B 组中第i个个体学习前和学习后的个体；如果A 组拥有最小适应度值，则o为B，如果B 组拥有最小适应度值，否则o为A；xo，i表示A 组或者B 组中第i个粒子。

在第二阶段，如图2 所示，进行P 群和T 群交流学习。比较P 群和T 群适应度值大小，将拥有最小适应度值粒子称之为xmin，并且拥有最小适应度值种群称之为优势种群，另一个种群为普通种群。粒子xmin使用TLBO 算法教学阶段的规则向普通种群中所有粒子进行教学，其更新公式为：

图2 子种群的信息交互Fig.2 Information interaction of subpopulations

其中：xh，old，i和xh，new，i分别是P 群或T 群中第i个个体学习前和学习后的个体；如果P 群拥有最小适应度值，则h为T，如果T群拥有最小适应度值，则h为P；xaver为普通种群适应度值均值。

整个种群在进行信息交互后，算法具有了良好的全局探索能力，又提高了收敛速度。

2.3 收敛性和多样性指标

为了使粒子收敛能力和多样性在进化过程中保持平衡，引入收敛性和多样性指标，分别用来计算粒子与最近邻粒子以及全局最优点s的距离。首先利用种群中适应度函数最大值和最小值对粒子xi进行归一化，这种归一化方法有助于消除振幅影响［19］。粒子xi归一化适应度函数f′(xi)为：

其中fmax和fmin分别是整个种群适应度函数最大值和最小值。

归一化多样性距离D反映粒子xi与最近邻粒子的距离，D较大则表示粒子xi距离它的邻居较远：

其中：dismax和dismin分别是整个种群中粒子之间最大和最小的欧氏距离，f″(xi)表示粒子xi与最近邻粒子的适应度值之差，如式（13）所示：

归一化收敛距离C反映粒子xi相对于理想点收敛能力［19］，C较大则说明粒子xi越接近理想点，如式（14）所示：

其中dis(xi)表示f′(xi)到理想点的欧氏距离。如式（15）所示：

对所有粒子按照式（11）～（15）进行收敛性和多样性计算后，将所有粒子收敛性和多样性按照式（16）进行加权：

将最大的mean(xi)值记为xleader。在t+1 次迭代后，如果xleader值没有更新，算法可能缺失多样性，并且陷入局部最优。因此，对所有粒子进行多项式变异：

其中：μi是分布在［0，1］内的随机数；η是分布指数，实验中η取11［20］。

2.4 TLPSO算法流程

TLPSO 算法具体步骤如下：

1）初始化所有粒子，种群大小为NP。

2）利用式（5）～（6）计算P 群、T 群大小，使用随机抽样的方法从T 群中选出相应粒子分配给P 群。

3）判断粒子是否属于P 群，如果是，则按照PSO 规则进行迭代：如果不是，则粒子属于T 群，再次判断粒子是否属于T 群中A 组；如果是，则按照TLBO 算法教学阶段进行迭代。如果不是，粒子属于T 群B 组，则按照TLBO 规则进行迭代。

4）信息交互第一阶段：T 群中A 组与B 组之间交流，普通小组向优秀小组中的学习粒子xl学习并产生后代。信息交互第二阶段：种群之间交流时，普通种群向优势种群中的粒子xmin学习产生后代。

5）先按照式（11）～（15）进行计算粒子收敛性和多样性，再根据式（16）判断xleader是否更新，没有则进行多项式变异。

6）如果满足迭代终止条件，则终止迭代，输出全局最优解；否则转到步骤2）。

3 仿真实验

3.1 测试函数

为了测试改进算法性能，本文采用15 个典型测试函数进行测试，给出了15 个函数的数学描述：

F1 函数：

其中：xi∈[-100，100]，维数D取30 和100，Global(fmin)为0。

F2 函数：

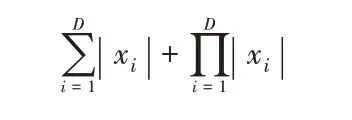
其中：xi∈[-10，10]，维数D取30 和100，Global(fmin)为0。

F3 函数：

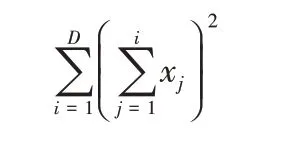
其中：xi∈[-100，100]，维数D取30 和100，Global(fmin)为0。

F4 函数：

其中：xi∈[-100，100]，维数D取30 和100，Global(fmin)为0。

F5 函数：

其中：xi∈[-30，30]，维数D取30 和100，Global(fmin)为0。

F6 函数：

其中：xi∈[-100，100]，维数D取30 和100，Global(fmin)为0。

F7 函数：

其中：xi∈[-1.28，1.28]，维数D取30 和100，Global(fmin)为0。

F8 函数：

其中：xi∈[-5.12，5.12]，维数D取30 和100，Global(fmin)为0。

F9 函数：

其中：xi∈[-32，32]，维数D取30 和100，Global(fmin)为0。

F10 函数：

其中：xi∈[-600，600]，维数D取30 和100，Global(fmin)为0。

F11 函数：

其中：xi∈[-5，5]，维数D取2，Global(fmin)为-1.031 6。

F12 函数：

其中：xi∈[-5，5]，维数D取4，Global(fmin)为0.000 307。

F13 函数：

其中：xi∈[0，1]，维数D取3，Global(fmin)为-3.86。

F14 函数：

其中：xi∈[0，1]，维数D取6，Global(fmin)为-3.32。

F15 函数：

其中：xi∈[-50，50]，维数D取30 和100，Global(fmin)为0。

3.2 算法设置

将提出的TLPSO 算法与粒子群优化算法（PSO）、协方差矩阵自适应进化策略（Covariance Matrix Adaptation Evolutionary Strategy，CMA-ES）算 法［21］、相量粒子群优化（Phasor PSO，PPSO）算法［22］、混合灰狼粒子群（Hybrid PSO and Grey Wolf Optimizer，PSOGWO）算法［23］、混合引力搜索的粒子群优化算法（PSO and Gravitational Search Algorithm，PSOGSA）［24］、重选精英个体的非线性收敛灰狼优化算法EGWO（improved Grey Wolf Optimizer algorithm using nonlinear convergence factor and Elite re-election strategy）［25］进行仿真对比。在实验中，所有算法的相关参数如表1 所示。对于所有的算法，群体大小设置为100，最大迭代次数是1 000。每种算法在实验中独立运行30 次，统计每个算法的测试函数平均值和标准差，平均值能够体现出算法的收敛能力，方差体现出算法的稳定性。

表1 不同算法参数设置Tab.1 Parameter settings for contrast algorithms

3.3 结果分析

表2～3 和图3 分别为改进算法与其他六种算法的对比结果和对照图。表格中：Ave 和Std 是30 次独立运行后所获得的平均值和标准差，加粗体字表示算法获得的最优值。图3中，除了测试函数F11、F13 和F14，其余测试函数的纵轴是采用对数处理后的数量级。

图3 低维收敛曲线对比Fig.3 Comparison of low dimensional convergence curves

表2 低维测试函数结果对比Tab.2 Experimental results comparison of low dimensional benchmark functions

从低维测试函数表3 中可以看到在测试函数F1、F2、F3、F4、F6、F7、F8、F9、F13、F14、F15 上，本文提出的TLPSO 算法性能明显优于其他六种算法，并且在测试函数F8、F10、F11、F12、F13、F14 上搜索到理论值，仅测试函数F5 上的优化性能微弱于CMA-ES。在12 个测试函数上，TLPSO 算法性能都优于PSOGWO 和PSOGSA，这说明粒子群优化算法与教与学优化算法的结合比上述两种算法优化效果更好，这是因为采用了指标加权策略，让粒子收敛能力和多样性在进化过程中保持平衡，提高了局部搜索能力，使TLPSO 算法可以获得更好的平均最优值。除了测试函数F4 和F12 以外，TLPSO 算法的标准差对于其他六种算法都是最好的，这表明TLPSO 算法具有良好的稳定性。

在表3 中，可以看到在多峰函数F10 上，CMA-ES、PSOGWO、PSOGSA、EGWO 和TLPSO 算法都搜索到了理论值0，但是在图4 的F10 上可以看出，TLPSO 算法收敛速度明显优于其他三种算法，在不到200 次迭代中就可以搜索到理论值0。对于测试函数F1、F2、F3、F4、F6、F9、F15 来说，TLPSO算法收敛精度和收敛速度都远超其他六种算法；而对于测试函数F7、F8、F12 和F14 来说，虽然TLPSO 算法前期收敛速度较慢，但是在收敛精度上也优于其他六种算法。这是由于教与学优化算法学习者阶段能够让粒子之间相互学习，提高全局搜索能力，从而探索到更多的可行域，使算法在求解精度上有了显著优势，并且通过动态调整种群规模，使TLPSO 算法在迭代后期仍保持良好的收敛速度。从高维测试函数表4 中可以看到，在测试函数F1、F2、F3、F4、F5、F7、F8、F9、F10、F15 上，TLPSO 算法相较于其他对比算法仍能找到更好的解，并且其算法性能相对于低维测试函数也没有明显下降，说明TLPSO 算法对维数不敏感。综上所述，TLPSO 算法与其他六种算法相比，具有更好的收敛性能和优化精度。

表3 高维测试函数结果对比Tab.3 Experimental results comparison of high dimensional benchmark functions

图4 是七种算法在低维测试函数F1、F2、F3、F4、F5、F6、F7、F9 和F15 上的最优解集箱线图，可以更加直观地对比七种算法在独立运行30 次后，最优解集分布情况。从整体上看，算法TLPSO 在测试函数F1、F2、F3、F4、F6、F7、F9 和F15上，都远比其他五种算法更接近理想值，在测试函数F5 上稍弱于算法CMA-ES，与表3 数据和图4 曲线一致，说明在大多数测试函数上，该算法收敛性能都远优于其他算法。从最优解集分布情况来看，算法TLPSO 在大部分测试函数上分布较小而其他算法分布较大，说明对大部分测试函数来说，算法TLPSO 的收敛性和稳定性效果更佳。因此，算法TLPSO 具有收敛速度快、寻优能力强、稳定性好的优点。

图4 低维最优解统计分布Fig.4 Low dimensional optimal solution statistical distribution

4 结语

针对单一种群在解决高维问题中收敛速度较慢和多样性缺失问题，提出了一种基于教与学信息交互粒子群优化算法。通过将种群动态地划分为两个子种群，分别采用粒子群优化算法和基于教与学的优化算法，通过子种群之间信息交互和收敛性和多样性指标，使粒子收敛能力和多样性在进化过程中得到平衡。为了验证TLPSO 的有效性，通过15 个Benchmark 测试函数，与PSO、CMA-ES、PPSO、PSOGWO、PSOGSA 和EGWO 算法在低维和高维测试函数上进行比较，实验结果验证了TLPSO 算法在收敛精度和收敛速度方面有着较为明显的改善效果。