基于GA-Adam优化算法的BP神经网络农业灌水量预测模型

王建辉，冉金鑫，沈莹莹，韩振中，崔远来，罗玉峰

（1.武汉大学水资源与水电工程科学国家重点实验室，武汉430072；2.中国灌溉排水发展中心，北京100054）

0 引言

农业水资源管理是区域水资源优化配置的重要环节，而合理配置农业水资源的前提是需要对农业灌溉用水量进行精确预测［1］。从机理层面看，农业灌溉用水量受区域降水量、蒸散量、灌溉面积、灌溉水利用系数等因素的影响，从宏观层面看，农业灌水量与区域水资源可利用数量、灌溉工程建设水平、农业结构调整和灌溉管理水平等诸多因素也存在着密不可分的联系［2］。因此农业灌水量的变化趋势既存在着可预见的规律性，又存在着一定的不确定性。要实现对其精确地预测，需要一种既能从机理层面解释，又能在高维非线性关系中找寻最优解的方法。人工神经网络模型便是一个比较合适的方法。

近些年国内外学者对神经网络应用于灌溉用水量预测做了许多探索性研究。徐建新［3］等提出BP 神经网络灌区灌水量预测模型，考虑了灌溉面积、年降雨量以及粮食产量对灌溉用水量的影响；方旭［4］等利用BP 神经网络模型，对辽宁锦州市为实例进行了灌水量预测，结果满足规范要求；张艺聪［5］利用BP神经网络模型郑州市农业灌溉用水量进行预测，预测精度较好。但这类方法采用传统神经网络模型算法，存在参数的初始值得不到优化、收敛速度慢等问题。迟道才［6］等在人工神经网络的基础上引入灰色预测方法，二者结合成并联型灰色神经网络预测方法。储诚山［7］等、严旭［8］等相继提出了基于遗传算法的BP 神经网络用水量预测模型，有效地提高了BP 神经网络的预测精度。Zhang［9］等通过非线性协整理论与小波神经网络相结合的方法，建立了灌溉水量小波非线性协整预测模型。但这类研究仍存在许多不足：并联型灰色神经网络和小波非线性协整预测模型只在中长期灌水预测中表现较好，在短期灌水预测中误差较大；单一遗传算法不能解决学习率固定导致的收敛速度缓慢问题。本文从原理角度分析了传统BP 神经网络在训练过程中存在的弊端，引入了GA 和Adam 两种优化算法，以黄河流域陇中片灌溉分区内7 个典型灌区的实测灌水数据为例，对GA-Adam-BP神经网络的性能进行了分析。

1 优化算法分析

1.1 传统GD算法存在的问题

BP 神经网络是一种按误差逆传播算法训练的多层前馈网络。模型运行过程包括正向传播和误差反向传播两部分。以3层BP 神经网络为例，如图1所示。首先，样本数据通过加权计算后，经过输入层、隐藏层以及输出层，然后通过激活函数，计算出网络输出值；最后将输出值从输出层到输入层反向遍历所有层，确定输出层与样本输出期望值之间的损失函数。当网络误差达到一定精度要求时，网络便训练成功［10］。

图1 3层BP神经网络结构图Fig.1 3-layer BP neural network structure diagram

在误差反向传播的过程中，梯度下降法（GD）是最原始的调整损失函数参数的方法。GD 法的原理是：当误差没有达到预设精度，将损失函数分别对权重w和阈值b进行求导，求得损失函数对应不同参数下的梯度dw和db，然后沿着负梯度方向进行迭代，就可以收敛到损失函数最小值［11］。迭代公式为：

式中：wt、bt是调整后的权值和阈值，wt-1、bt-1是待训练的权值和阈值，α是学习率，dw、db是梯度。

传统GD法存在着以下两个问题：

（1）参数的初始值选择问题。初始权值w和阈值b一般是模型设计者给出的参数，初始值选择不同，获得的最小值也有可能不同。因此GD 法求得的结果从理论上看只是局部最小值，除非损失函数是凸函数。因此传统GD 法存在着局部最优解而非全局最优解的风险，需要多次用不同初始值运行算法，选择损失函数最小化的初值。

（2）学习步长的选择问题。学习率α指定了反向传播过程中梯度下降的步长，在GD 法中，学习率α从始至终是固定不变的，学习率太小会导致收敛速度过慢，而学习率太大会阻碍收敛，同时还会导致损失函数在极小值周围波动甚至背离。因此选择合适的学习率变得尤为重要。

1.2 引入GA算法后的改进方案

遗传算法（GA）是一种并行随机搜索最优化方法。其基本要素包括：染色体编码、适应度函数、遗传操作和运行参数［12］。在本文中使用的编码方法为实数编码，每个个体均为一个实数串，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值共4 部分组成。由于个体包含了神经网络全部权值和阈值，因此在网络结构已知的情况下，就可以构成一个确定的神经网络。适应度函数F为预测输出和期望输出之间的误差绝对值和，函数表达式为：

式中：k为系数；Ti为期望输出值；为预测输出值。

然后通过GA 法中选择、交叉和变异操作找到最小适应度值对应个体，从全局得到最优个体对网络初始权值w和阈值b的赋值。因此引入GA 法可以实现对初始权值和阈值的预筛选，同时还可解决传统GD 法存在着局部最优解而非全局最优解的缺点。

1.3 引入Adam算法后的改进方案

Adam 算法来源于适应性矩估计（Adaptive Moment Estimation），是一种使用动量和自适应学习率来加快收敛速度的优化算法［13］。引入动量因子是为了抑制GD 法在收敛过程中的震荡作用。与GD 法相比，Adam 算法不直接使用梯度，而是用各个时刻梯度的指数移动平均值来代替GD 法中的梯度，也即是梯度的一阶矩估计，其表达式为：

式中：mt-1、mt分别为迭代前、迭代后的一阶矩估计；β1为指数加权平均参数；dk代表权值w或阈值b的梯度。

自适应学习率算法实质上是采用了梯度的二阶矩估计［14］。二阶矩估计表达式为：

式中：vt-1、vt分别为迭代前、迭代后的二阶矩估计；β2为指数加权平均参数；dk2代表权值w或阈值b的梯度平方。

将上述一阶动量mt、二阶动量vt结合在一起，对权值和阈值进行更新，表达式如下：

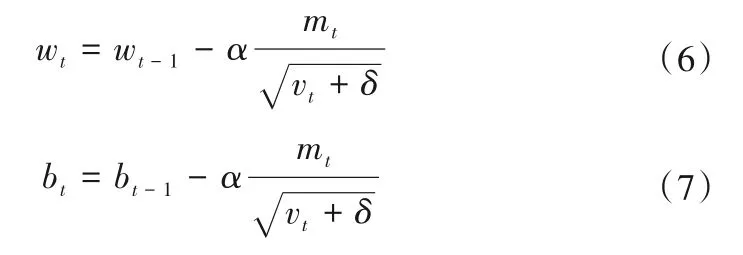
式中：wt、bt为调整后的权值和阈值；wt-1、bt-1为待训练的权值和阈值；α为学习率；δ为常数。

由式（6）和（7）可看出，Adam 算法利用一阶矩估计mt代替GD 法的梯度，从而控制权值或阈值的调整方向；利用二阶矩估计vt调整学习率的大小，让学习速率自适应于梯度变化，从而解决GD法难以选择学习率和影响模型收敛的问题。

2 模型的构建

2.1 GA-Adam-BP神经网络的构建

本文将GA 算法和Adam 算法同时应用到BP 神经网络的农业灌水量预测模型中，算法流程图如图2所示。

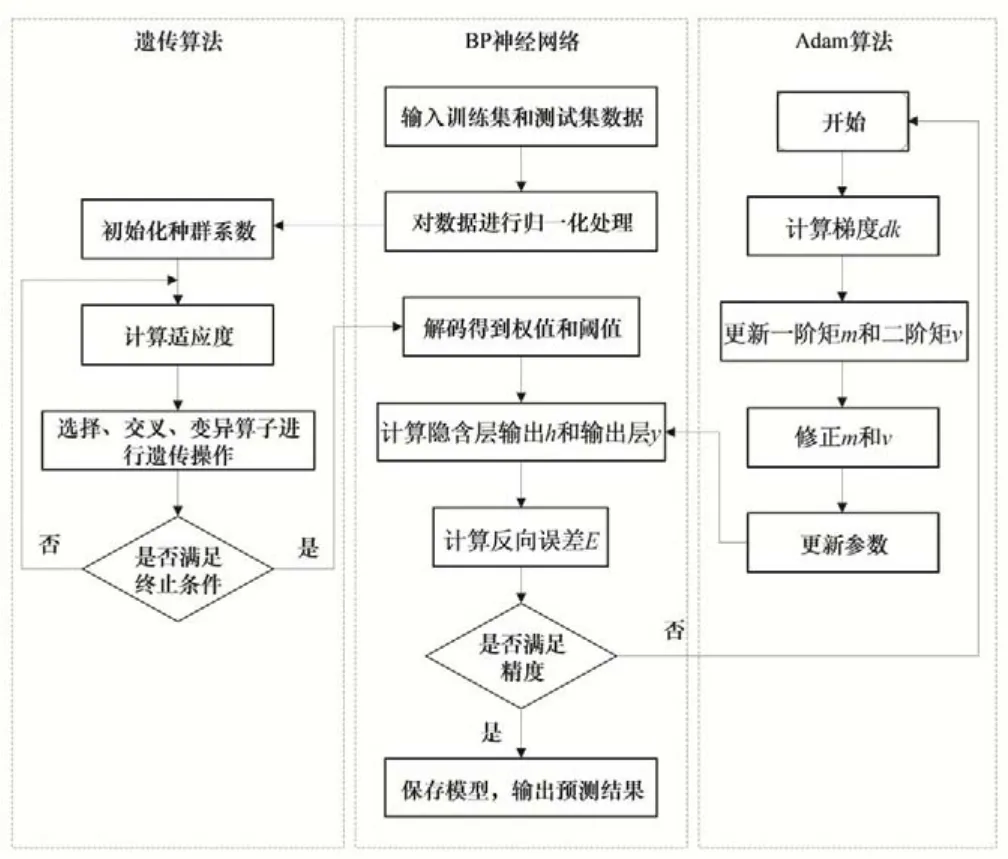
图2 GA-Adam-BP神经网络流程图Fig.2 GA-Adam-BP neural network flow chart

2.2 样本数据简介

样本数据为黄河流域陇中片灌溉分区内典型灌区的气象资料和作物实测灌水资料。典型灌区包括：兴电灌区、贾崖张井五家沟灌区、发源灌区、菜子口灌区、沣泰渠灌区、永固渠灌区、马寨南井灌区等7个灌区。样本数据主要包括：

（1）气象资料。气象资料包括典型灌区对应7 个气象站点的2015年1月1日-2018年12月31日的逐日气象数据，数据来源于中国气象数据网（http：//data.cma.cn/）。

（2）实测灌水资料。7 个典型灌区的玉米实测灌水资料（2015-2018年）。利用气象资料整理月降雨量，月ET0等因素作为模型输入层，从水量平衡机理层面解释农业灌水量的变化趋势；同时加入时间序列因子，增强模型的短期预测能力。以7个典型灌区2015-2017年的数据作为模型的训练集，2018年的数据作为测试集。表1 为兴电灌区的训练集与测试集数据示例。由于灌区实测灌水数据不全，有些年份和月份的实测灌水量是空值，将空值日期剔除后，共计64 组训练数据，14 组测试数据。

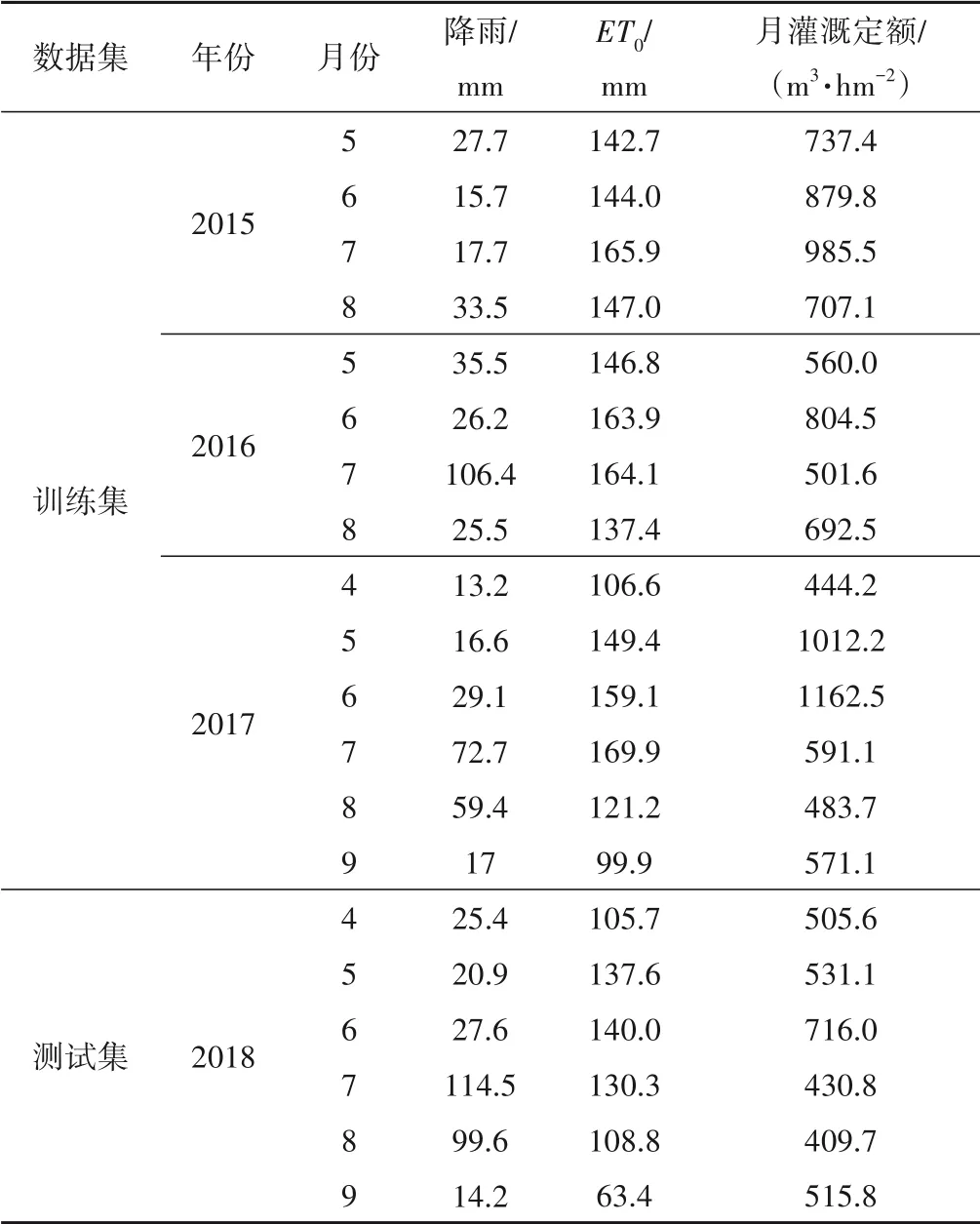
表1 兴电灌区训练集与测试集数据Tab.1 Xingdian Irrigation Area training samples and test samples

2.3 模型参数设置

（1）BP神经网络参数设置。以样点数据中月ET0、月降雨以及月份序列作为模型的输入层，输入节点为3。月灌溉定额作为模型的输出层，输出节点为1。从理论来看，当BP 网络结构为3 层时，可以无限趋近于任何有理函数。考虑本模型输入层节点数并不多，设置过多隐含层数容易导致过拟合现象。因此，将隐含层数设为1，隐含层节点数设为12。初始权重w和阈值b均设为0.5，训练结束次数设为5 000。

（2）GA 和Adam 算法参数设置。GA 法参数设置：种群规模为10，进化次数为50 次，交叉概率为0.4，变异概率为0.2。Adam 算法参数设置为：初始学习率α设为0.001，一阶矩、二阶矩估计的指数加权平均参数β1和β2分别设为0.9 和0.999，δ取值为10×10-8。

3 模型的性能评价

3.1 模型训练性能分析

本文分别使用GD算法、GA算法、Adam算法以及GA-Adam算法对BP 神经网络进行训练，共建立4 种农业灌水量预测模型，模型参数设置保持一致，以此检验GA-Adam 优化算法性能的好坏。

图3 为4 种算法在实际训练过程损失函数变化图。对比4种模型误差收敛速度，其中GA 法无法在指定训练次数达到预设精度，在训练次数达到5 000次仍未达到预设精度。由图3可看出，训练次数达到1 400 次左右时，GD 法的损失函数基本收敛在0.022 5附近，这说明传统BP神经网络模型学习能力不够，未能捕捉到样本数据集的特征信息；GA 法可以改进传统梯度下降法收敛速度慢的缺点，在训练次数达到1 084 次时，损失函数值降为0.001，达到预设训练精度；Adam 法能够快速收敛，在训练93 次时达到预设精度。GA-Adam 法所需训练次数最少，在训练67次时达到预设精度。

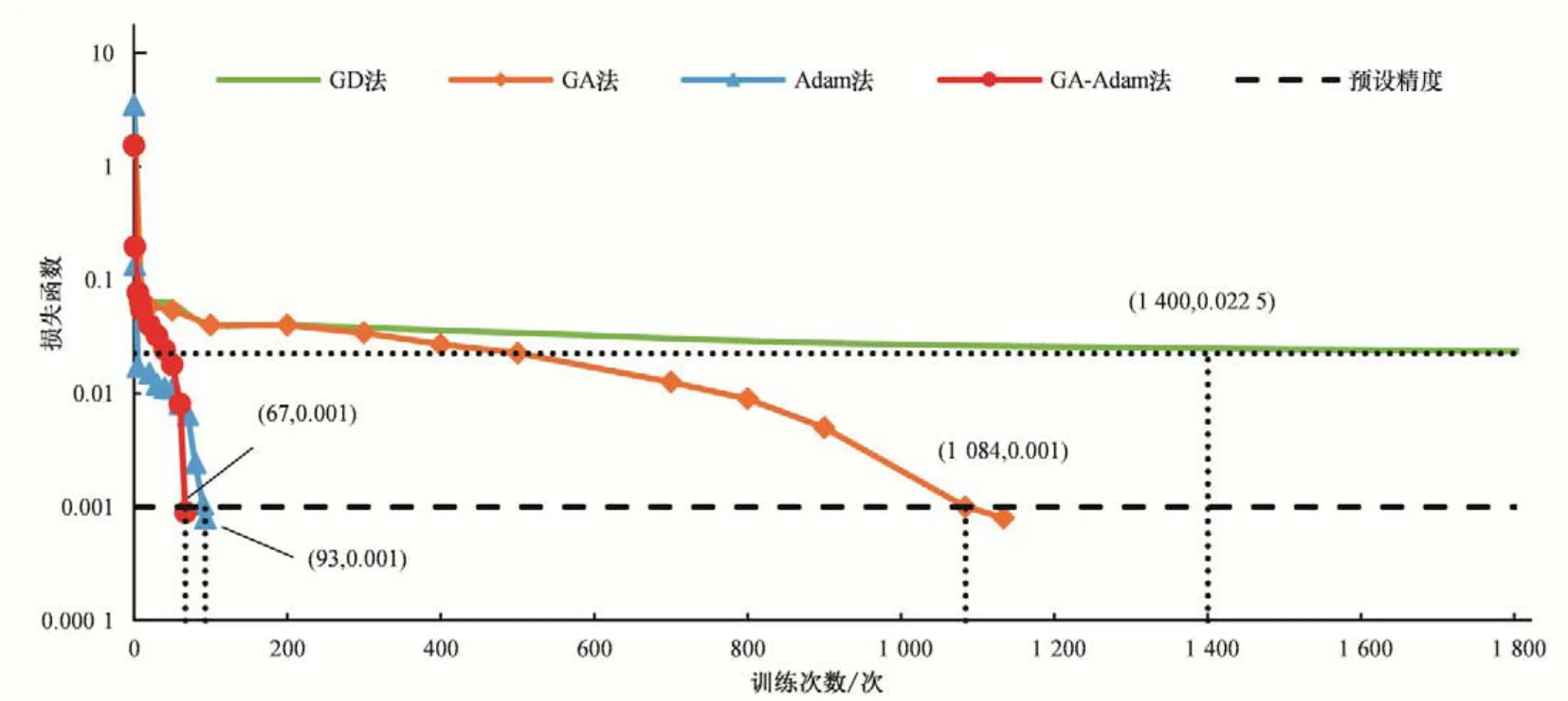
图3 不同算法的损失函数变化图Fig.3 Variation diagram of loss function of different algorithms

图4 是4 种算法的训练时长对比图。GD 法在训练过程中速度基本保持恒定，这可能是因为GD 法保持恒定学习率进行训练导致的结果。GD 法在预设5 000 次训练次数的限制下，用时3.926 s，而其损失函数在第1400 次训练次数时基本达到收敛，此时训练时长为1.113 s，同比其他算法依旧用时最多；GA法在训练末期速度加快，总训练时长达到0.966 s；Adam 法和GA-Adam 法在10 次训练次数以内，训练速度均较为缓慢，随后逐渐加快，在训练末期速度减慢。总训练时长达到0.528 s 和0.403 s。

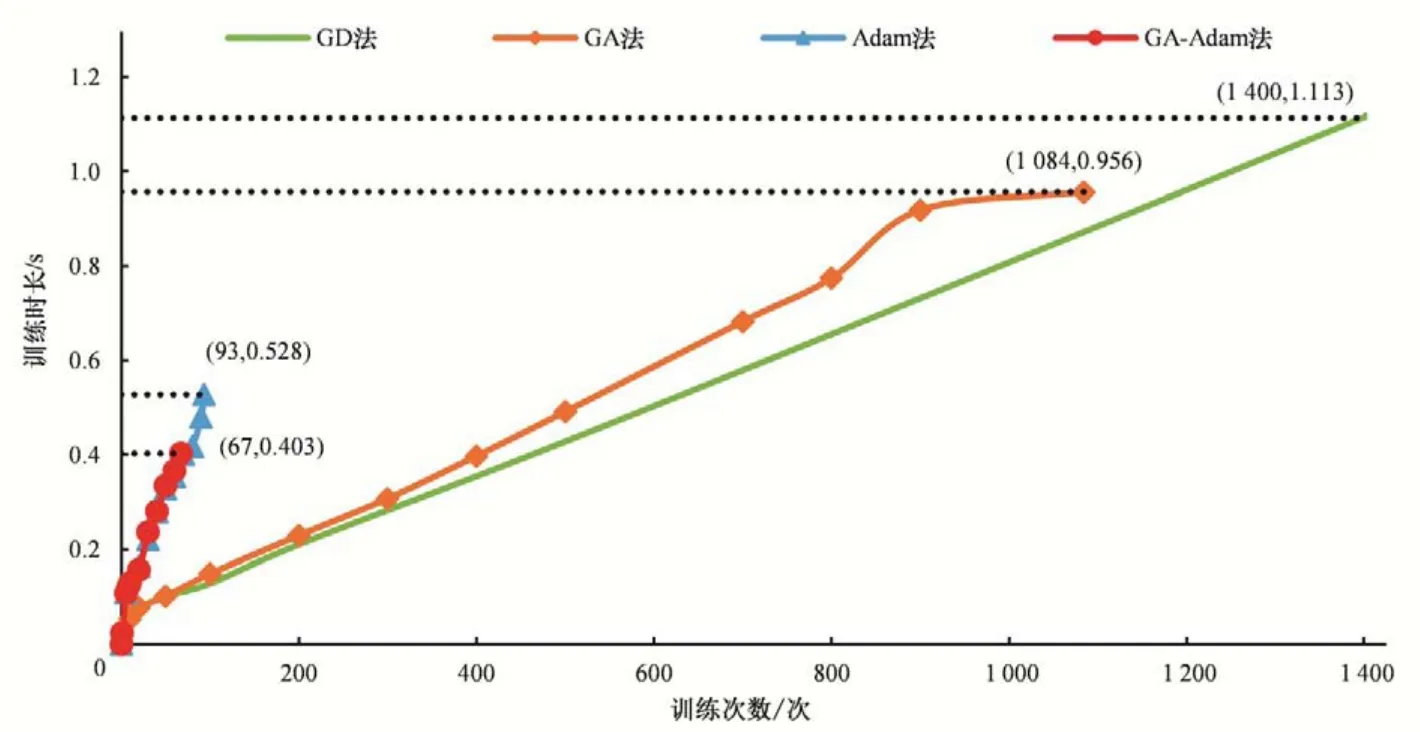
图4 不同算法的训练时长对比图Fig.4 Comparison of training duration of different algorithms

因此，结合训练精度和时长来看，GA-Adam法最为高效，仅在训练次数为67 次，训练时长为0.403 s 时就达到模型预设精度。

3.2 模型预测结果分析

图5 为4 种算法模型预测值与期望值的对比图。从图5 中可看出，GD 法和GA 法的预测值曲线变化趋势与实测值的变化趋势大致一致，除了个别与测试样本数据相差较大，例如GD 法与测试样本序列第3、6、9、11 的误差较大，GA 法与测试样本序列2、4、7、9 的误差较大。总体来看GD 法和GA 法的预测值与实测值之间的拟合情况一般。GD 法预测效果更差，GA 法相对较好。Adam 法和GA-Adam 法的预测值拟合效果较好，预测值曲线均大致分布在实测值附近，该两种方法较GD 和GA 法来看明显更优。

图5 不同算法模型预测值与实测值的对比图Fig.5 Comparison between predicted and measured values of different algorithm models

为了定性分析二者的优劣性，进行4 种算法预测值与实测值的回归分析。图6为预测值与实测值的回归分析图。采用均方根误差RMSE）、平均绝对误差MAE和决定系数R2等统计指标对预测值进行精度评价。均方根误差RMSE、平均绝对误差MAE越小，决定系数越接近1，预测值和实际值越接近，预测效果越好。表2 为4 种算法模型预测误差表。由表1 和图6 可看出，随着算法的改进，4种算法的均方根误差和平均绝对误差逐渐减小，预测误差从大到小的算法依次是GD 法、GA 法、Adam法、GA-Adam 法，GA-Adam 法的RMSE和MAE分别为54.73 和47.76。从决定系数R2来看，从大到小顺序为GA-Adam 法、Adam法、GA法、GD法，其中GA-Adam 法的R2为0.81，最接近于1。综上所述，不论从模型训练速度还是从预测结果精度来看，均是GA-Adam法为最佳优化算法。

表2 不同算法模型预测误差表Tab.2 Prediction error table of different algorithm models

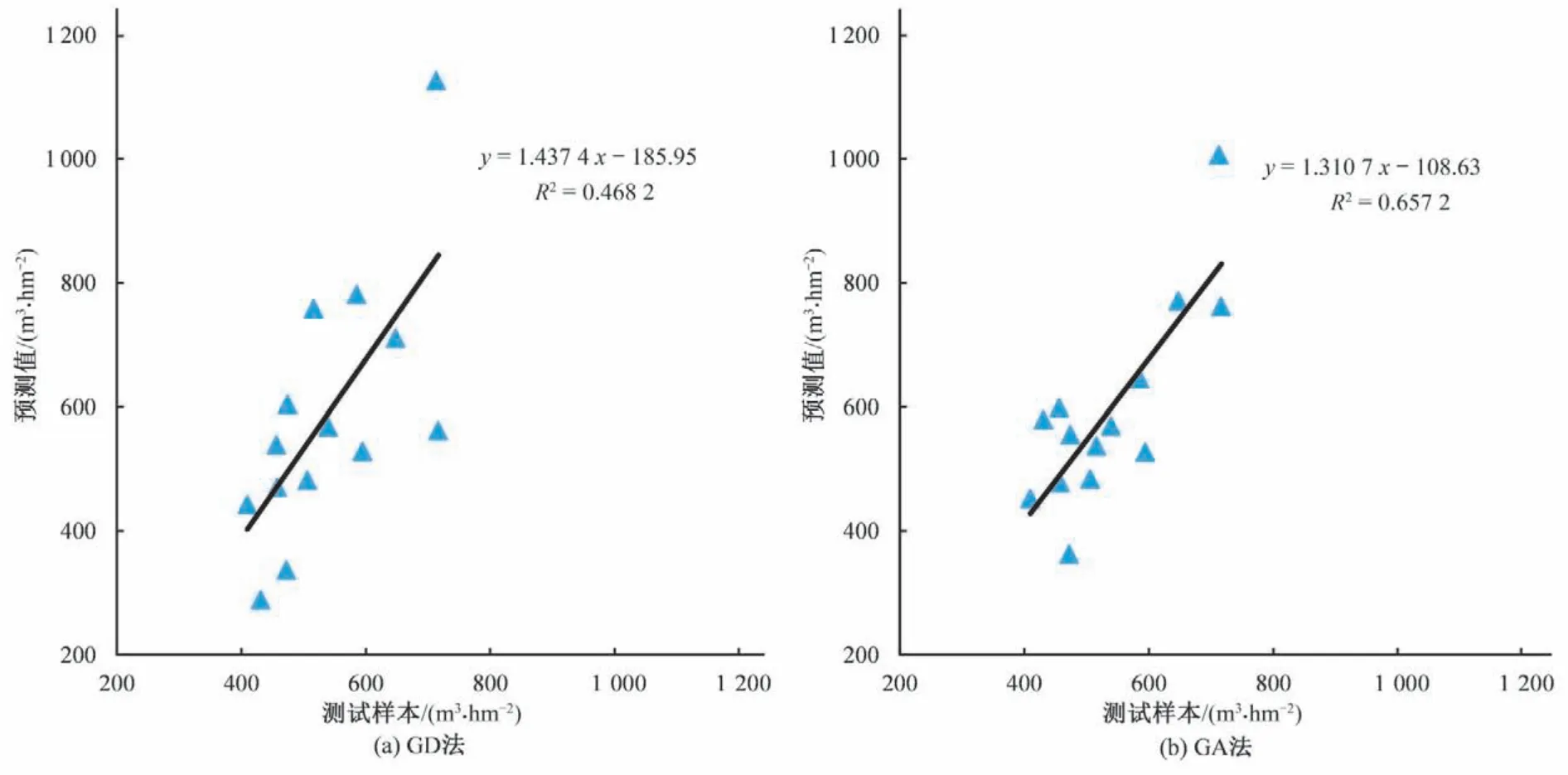
图6 不同算法模型预测值与实测值的对比图Fig.6 Comparison between predicted and measured values of different algorithm models

4 结论

GA-Adam算法在训练过程中表现出极高的精度，同时收敛速度最快，仅在训练次数为67 次，训练时长为0.403 s 时便达到预设精度；在模型测试误差分析中，GA-Adam 模型预测值与期望值的RMSE和MAE分别为54.73和47.76，决定系数R2为0.81，同样是GA-Adam 算法预测精度最好。综上所述，本文基于GA-Adam 优化算法的BP 神经网络农业灌水量预测模型，在农业灌水量预测方面有较高的可靠性和较好的应用性。□