基于CEEMD-TD模型的月径流随机模拟

王倩丽，马细霞，2，赵 璐，张静文，程 旭

（1.郑州大学水利科学与工程学院，郑州450001；2.郑州大学黄河生态保护与区域协调发展研究院，郑州450001；3.郑州航空港兴港投资集团有限公司，郑州450001；4.商丘工学院土木工程学院，河南商丘476000）

0 引言

水文随机模型是依据水文过程观测资料，分析水文过程随机变化特性的一种数学模型，其随机模拟的大量水文序列对于水资源评价、水库调度方案编制、各种水利参数确定等具有重要应用价值。解集类模型形象、简单、充分利用样本信息，能够进行多季节和多站点的水文序列模拟，在多个时间尺度或空间尺度上总量与分量序列的主要统计特性如均值、方差和协方差结构等能够得以保持，并且遵循了水量平衡［1］，因此被广泛地应用于水文模拟当中。徐利岗［2］等运用季节性随机模型的理论方法建立洛河状头站典型解集（TD）模型，经实用性检验，月径流模拟序列与实测序列各项统计参数吻合良好，符合精度要求。梅超［3］等以平寨水库入库径流随机模拟为例，分别采用双层模型法和典型解集法分解模拟月径流，其模拟结果显示典型解集分解法较双层模型分解法能更好地保持月径流的统计特性。TD模型具有直观、方便、能充分利用实测样本资料信息等优点，且解集而得的序列没有引入任何与概率分布有关的假定，可以全面反映样本序列的统计特性，但其在模拟过程中仅适用于平稳序列的随机模拟，具有一定的局限性［4］。

Huang 等［5］首次提出经验模态分解（EMD）法，该方法认为任何一个复杂的时间序列都可由EMD 分解为有限数量的本征模态函数（IMF），分解得到的原始信号与EMD 的近似正交基是随信号的变化而变化的，因而使得EMD 具备了更强的自适应性，更有利于非平稳数据处理［6］；Wu［7］等在对白噪声进行EMD分解深入研究的基础上，提出了集合经验模态分解（EEMD）法，以期遏制EMD 分解的模态混叠现象；EEMD 分解算法虽然可以通过增加白噪声来解决频率混叠问题并提高信号分解能力和算法稳定性，但是不能完全降低白噪声，因此在EEMD 算法基础上，CEEMD 算法通过在信号中增加分解次数来降低对符号的相反噪声，有效解决白噪声对误差精度的影响问题［8］；王燕鹏等基于CEEMD 具有非平稳信号平稳化的能力构建了CEEMDBP 灌区地下水埋深预测耦合模型，结果表明CEEMD-BP 耦合模型和其他模型相比具有较好的预测效果［9］。

本文以黄河流域的3 个典型水文站为例，将对非平稳序列有较强处理能力的互补式集合经验模态分解（CEEMD）法引入到径流随机模拟中，提出一种新的互补式集合经验模态分解-典型解集（CEEMD-TD）模型，通过检验截口的主要统计参数来评价随机模型的模拟效果，以验证该随机模型的可靠性。

1 CEEMD-TD模型介绍

TD模拟月径流的思路是：先对剔除确定性成分后的各站年径流随机序列进行平稳性检验，然后对平稳的实测的年径流量建立随机模型，采用自回归AR（p）模型进行随机模拟，得到模拟的年径流序列。在各站年径流实测系列中分别找出与每个年径流模拟量最为接近的那个值，以此为典型年，按照该年各月径流量占全年径流量的分配系数，对模拟的年径流量进行缩放，得到模拟的月径流序列。

CEEMD-TD 模型是对TD 模型的改进，其过程仍分为两大步，即年径流自回归随机模拟和年径流月分配过程的确定。具体思路是：①建立年径流CEEMD-AR 随机模型，首先剔除年径流实测序列中非周期成分与周期成分，剔除确定性成分后的随机序列进行CEEMD 分解，得到一组固有模态函数（IMF）分量和残差序列；对每个IMF 分量进行ADF 平稳性检验，经平稳检验后的各个IMF 分量进行AR（p）模型随机模拟，然后对残差序列进行多项式拟合；将随机模拟后的各IMF 分量序列与多项式拟合后的残差序列进行重构，并在此基础上还原实测序列中的确定性成分，便得到模拟的年径流序列；②月径流随机模拟，在年径流实测系列中找出与每个年径流模拟量最为接近的那个值，以此为典型年，按照该年各月径流量占全年径流量的分配系数，对模拟的年径流量进行缩放，得到模拟的月径流序列。

其中，CEEMD方法的具体步骤如下［11］：

（1）设原始信号为x(t)，为克服模态混叠，向其添加白噪声，使得信号分布到合适的振荡尺度上。白噪声记为ωi(t)，将原始信号与噪声叠加，得：

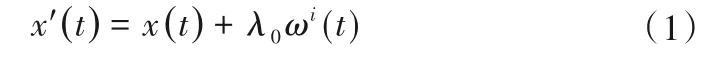
式中：λ0表示噪声系数。

（2）将信号x′(t)的局部极大值点用一条曲线连接起来，定义为上包络fmax（t）；同样将所有的局部极小值点也用一条曲线连接定义为下包络fmin（t）；并设上、下包络的平均值为m（t），则有：

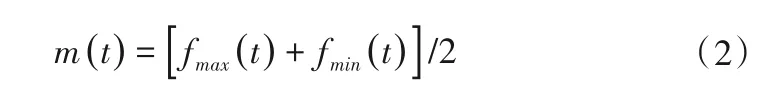
（3）将信号x′(t)与包络的平均值m（t）作差运算：

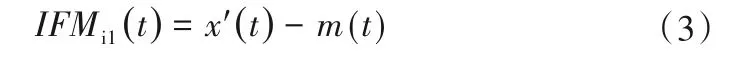
（4）对信号x′(t)分解N次，即重复N次步骤（2）、（3），得到第一个IMF分量：

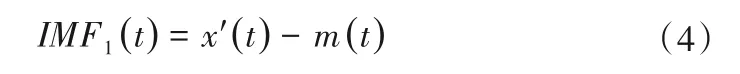
（5）得到第一个IMF分量IFM1（t）后，剩余信号用r1（t）表示：

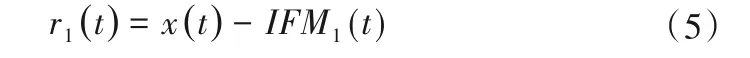
（6）继续执行以上步骤，将信号r1(t)+λ1E1[ωj(t)]进行N次分解，第二次分解后的结果可以表示为：

（7）对分解得到的模态分量用Ei表示，则第j个剩余的分量可以表示为rj（t）。

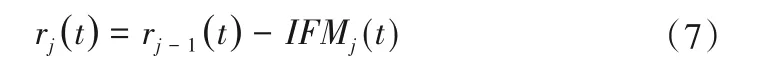
（8）对某次分解后的信号r1(t)+λ1Ej[ωj(t)]，对其再次进行分解，可以得到j+1个分量，表示形式如下：

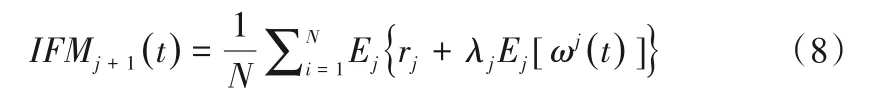
（9）重复执行以上过程，直至某次IMF分量不可再分时，停止分解过程。可以得到J个分量，将最终的残差值记为：

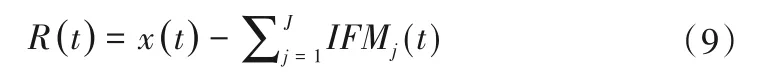
（10）整理以上公式可得原始信号x（t）表达如下：

2 实例应用

2.1 研究区概况

河南省位于我国中东部、黄河中下游，界于东经111°21′～116°39′和北纬31°23′～36°22′之间，全省总面积16.7 万km2，占全国总面积的1.73%。黄河干流自灵宝市进入河南境内，流经三门峡、济源、洛阳、郑州等8 个省辖市和27 个县（市、区），河道总长711 km，流域面积3.62 万km2，占黄河流域总面积的5.1%。为深入研究河南省黄河流域的水文情势，验证CEEMD-TD 模型的适用性，本文分别选择黄河流域的黑石关站、花园口站、白马寺站等具有较长径流实测资料且集水面积不一的典型水文站作为研究对象，各典型水文站的地理位置如图1所示。

图1 典型水文站示意图Fig.1 Schematic diagram of a typical hydrological station

2.2 数据来源

收集各典型水文站的径流实测资料作为基础数据资料，以期为径流序列的模拟与分析提供理论支持，详细信息见表1。资料来源于《河南省水情手册》，数据年限较长，资料经过审查，且数据全面、合理。

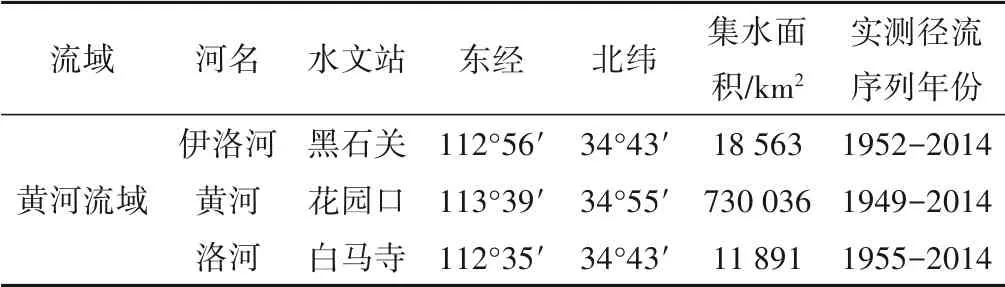
表1 典型水文站信息表Tab.1 Typical hydrographic station information table

2.3 年径流序列平稳性检验

CEEMD-TD 模型随机模拟的基本思路是先对年径流随机序列（不含非周期成分与周期成分）进行随机模拟，再将随机模拟得到的大量年径流序列分解为月径流序列。因此，开展CEEMD-TD 模型随机模拟前，需剔除年径流实测序列中非周期成分与周期成分，得到年径流随机序列，对剔除确定性成分后的序列随机项进行CEEMD分解和ADF平稳性检验。

2.3.1 非周期性成分识别

（1）趋势诊断项。采用Mann-Kendall 检验法［12］、Spearman秩相关检验法［13］分别对黑石关站、花园口站和白马寺站的年径流实测序列进行趋势项检验，结果见表2。

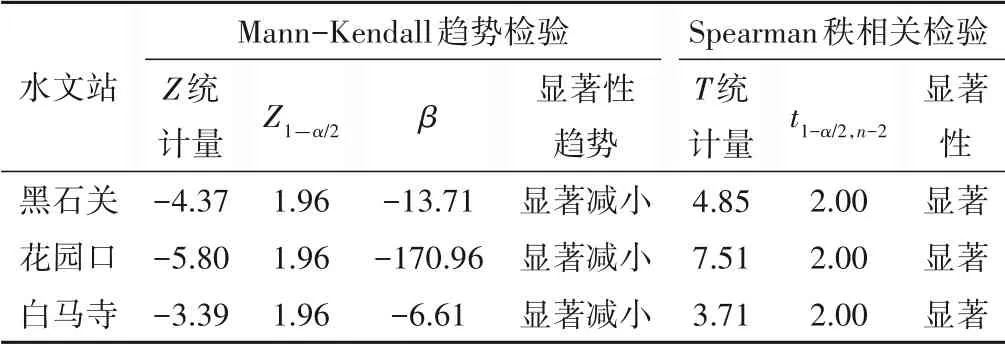
表2 各站趋势检验结果Tab.2 Trend test results of each station

结果表明：Mann-Kendall 检验法下黑石关站等3 个水文站年径流实测序列统计变量Z的绝对值均大于临界值Z1—α/2，且变化趋势β均小于0，说明各站年径流实测序列均具有显著的减小趋势；此外，Spearman秩相关检验法计算得各站统计量T的绝对值均大于自由度为n-2 的t分布在α=0.05 显著水平下的临界值t1-α/2，n-2，说明该趋势显著，结果表明Spearman 秩相关检验法的检验结果与Mann-Kendall检验法一致。

剔除趋势项成分后，黑石关站等3 个水文站年径流分解序列和实测序列的线性趋势对比见图2。

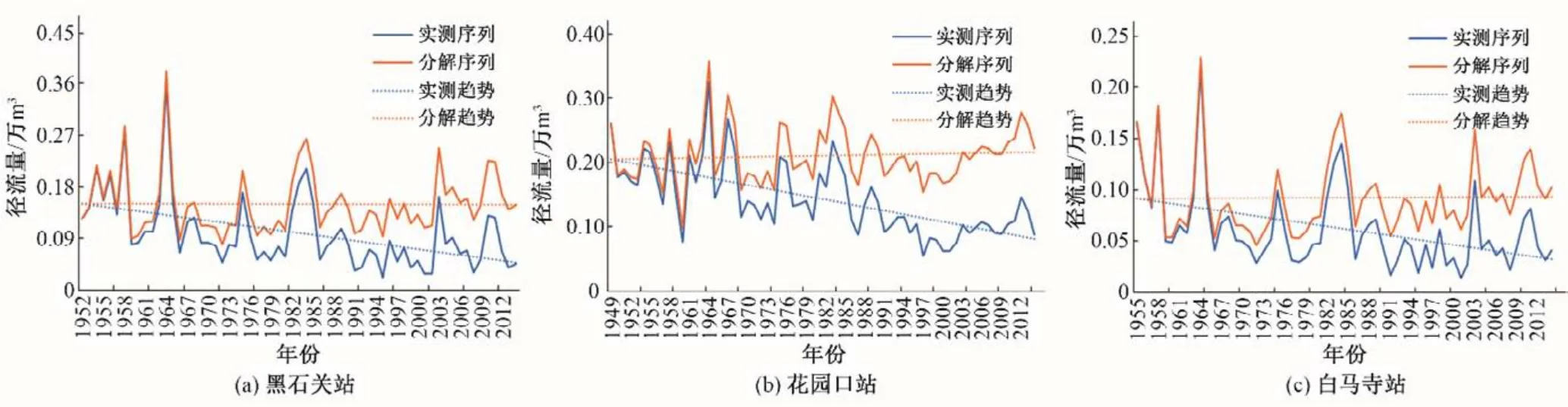
图2 各站年径流序列分解前后过程图Fig.2 Process diagram before and after decomposition of annual runoff sequence of each station

根据图2 趋势项诊断结果，可看出黑石关站等3 个水文站分解后的年径流过程线更加平缓，线性趋势更加平稳，趋近水平线，并在0.05显著性水平下对3个水文站分解后的各年径流序列进行一致性诊断，结果表明分解后的各序列不存在显著性趋势。

（2）跳跃诊断项。采用Mann-Kendall 突变检验法对黑石关站等3 个站分解后的年径流序列进行跳跃项检验，检验结果见图3。选取统计曲线UB和UF在临界区间内的交点作为最可能变异点。

由图3 可知，黑石关站、花园口站、白马寺站年径流序列的最可能变异点分别为2002年、2009年及2007年，引起变异的主要原因是在20世纪90年代后分别发生了3次大水灾和旱灾，以及大规模水利水电工程、农田设施建设、城市化进程和水土保

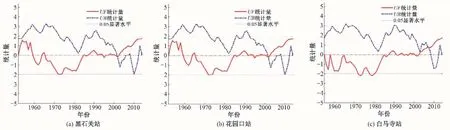
图3 各站年径流序列变异检验结果Fig.3 Test results of annual runoff sequence variation at each station

持工程等人类活动的影响，改变了下垫面水文过程的形成条件以及水循环的途径与速度。根据跳跃项诊断结果，对存在跳跃项的序列进行预处理，即将变异点之后的序列加上变异前后两序列均值之差，从而剔除确定性成分中的跳跃项部分。

将各站年径流序列从变异点处开始重新绘制过程线和趋势线，并与还原变异前的序列进行对比，结果如图4所示。

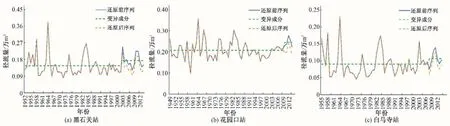
图4 各站年径流序列变异前后过程图Fig.4 Process diagram before and after variation of annual runoff sequence of each station

对黑石关站等3个水文站剔除趋势项和跳跃项后的年径流序列进行跳跃项诊断，结果表明经上述预处理后的各序列不存在显著性变异。

2.3.2 周期性成分识别

对经过预处理后的各水文站年径流序列xt采用方差线谱法进行周期分析，根据Fourier 级数的理论，分别计算出各站ωj对应的。

取显著性水平α=0.05，对各站查F分布表分别得到相应的F0.05（2，n-2-1），以黑石关站为例，黑石关站仅F7（4.23）大于F0.05（2，60），即其第7 个谐波显著，则黑石关站年径流序列有一个9年的显著周期。各站年径流序列周期项的相应统计量见表3，其中，aj、bj、Aj为第j个谐波的Fourier 系数，ωj为对应谐波的角频率，Tj为频率ωj对应的周期。

表3 各站年径流序列周期项统计量Tab.3 Periodic statistics of annual runoff sequence of each station

分别将各水文站相关统计量代入周期项公式，识别出各水文站年径流序列的周期项。以黑石关站为例，该站年径流序列的周期项为：

在剔除非周期成分的年径流序列基础上，剔除周期项，最终可得序列随机成分。根据各站得到的年径流随机序列重新绘制过程线和趋势线，并与还原周期成分前的年径流序列进行对比，结果如图5所示。

图5 各站年径流序列还原周期前后过程图Fig.5 Process diagram of the annual runoff sequence of each station before and after the restoration cycle

对各站剔除确定项成分后的年径流序列进行周期成分识别，结果表明各站经上述处理后的序列均不存在周期成分。

2.3.3 单位根平稳性检验

对剔除确定性成分后的各站年径流随机序列进行ADF 单位根法检验其平稳性，结果发现：黑石关站年径流随机序列为非平稳序列，不能直接采用AR 模型进行随机模拟；花园口站、白马寺站的年径流随机序列均为平稳序列，均可采用AR 模型进行随机模拟。

为解决黑石关站年径流随机模拟问题，同时也为了提出一种新的、精度高于AR 模型的年径流随机模型，本文根据确定性成分识别成果，将剔除趋势项、跳跃项和周期项后的黑石关、花园口和白马寺3个水文站年径流随机序列进行CEEMD 分解，总体平均次数N取为200 次，噪声标准差为原始序列标准差的20%。经CEEMD 分解后分别得到3 个水文站的各阶固有模态函数IMF序列及残差序列，如图6所示。

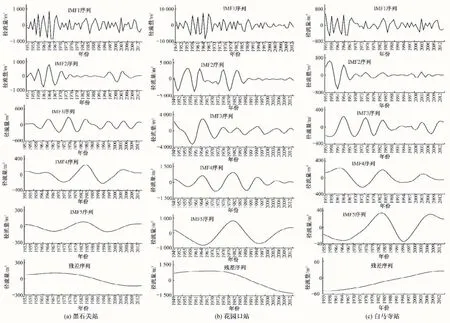
图6 各站年径流随机序列CEEMD分解结果Fig.6 CEEMD decomposition results of annual runoff random sequence at each station

经CEEMD 分解后黑石关站等3 个站的IMF 序列的|t|值均大于显著性水平α=0.05 时对应的临界值|t0.05|，且p值均小于0.05，即各站IMF 序列均为平稳序列，可采用AR 模型进行随机模拟。

2.4 年径流随机模拟

（1）残差序列的多项式模拟。采用多项式随机模拟法对黑石关站等3 个水文站经CEEMD 分解后的趋势项序列分别进行模拟，模拟结果如下：

式中：Rti为各站趋势项模拟值（i=1 表示黑石关站；i=2 表示花园口站；i=3表示白马寺站）；t为年份序号。

（2）各站年径流序列AR 模型建立。建立IMF1～IMF5 序列对应的AR 模型，采用RIC 准则进行AR 模型模式识别，确定模型阶数。其中AR（p）模型的数学表达式见下式，各站年径流序列AR模型参数见表4。

表4 IMF1～IMF5序列AR模型参数Tab.4 AR model parameters of IMF1～IMF5 sequence

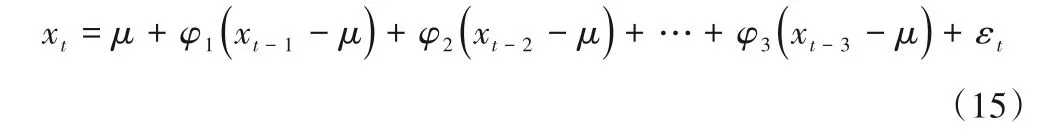
式中：μ为序列均值；σ为序列标准差；φ1，φ2，…，φp为自回归系数；εt为纯随机序列。

（3）年径流序列生成。将黑石关站等3 个水文站的各IMF序列的AR模型分别进行随机模拟，均模拟出100组与实测年径流序列样本容量相同的序列；然后将各IMF 序列模拟结果与趋势项模拟结果求和，并在此基础上还原实测序列中的确定性成分，即可分别得到基于CEEMD-AR 模型的各水文站100组年径流模拟序列。

为检验随机模拟生成的年径流序列是否具有实测序列相近的统计特征，本文选取年径流主要统计参数：均值、均方差σ、离势系数Cv、偏态系数Cs、一阶自相关系数r1和二阶自相关系数r2为检验指标，通过随机生成序列与实测径流序列统计参数的相对误差评价模型精度。分别计算黑石关、花园口和白马寺站年径流模拟序列各统计参数的平均值，并与各站年径流实测序列相应统计参数进行对比分析，其相对误差的绝对值ARE（以%表示）如表5所示。由表5可知，黑石关站等3个站年径流模拟序列的各项统计参数与年径流实测序列相应统计参数的相对误差均小于10%，说明各站的模拟序列均能较好地反映年径流实测序列的统计特性。

表5 各站年径流实测、模拟序列统计特性比较Tab.5 Comparison of statistical characteristics of annual runoff measured and simulated series at each station

为进一步分析CEEMD-AR 模型年径流模拟的精度，本文对剔除确定性成分后的花园口站和白马寺站的年径流随机序列建立AR 随机模型，并将随机模拟结果与实测序列中的确定性成分叠加，得到基于AR模型的花园口站和白马寺站100组年径流模拟序列。从两水文站年径流模拟序列统计参数相对误差的绝对值ARE（见表5），可以发现：花园口站CEEMD-AR 模型年径流模拟序列统计参数的相对误差均小于AR 模型，且其最大的相对误差仅为4.4%，白马寺站中除CEEMD-AR 模型的均值的相对误差略大于AR 模型之外，其余统计参数的相对误差均小于AR 模型，说明CEEMD-AR 模型相较于AR 模型可以更好地反映年径流实测序列的统计特性。

2.5 月径流模拟序列生成

对基于AR 模型与CEEMD-AR 模型的100年径流模拟序列，在各站年径流实测系列中分别找出与每个年径流模拟量最为接近的那个值，以这一年为典型年。按照该年各月径流量占全年径流量的分配系数，将与之对应的年径流模拟量进行解集，最终黄河流域的三个典型水站相应的随机模型均模拟出100组与各站月径流实测序列样本容量相同的月径流随机模拟序列。

为验证CEEMD-TD 模型的可靠性，选择月径流序列各截口主要统计参数：均值、均方差σ、离势系数Cv、偏态系数Cs、一阶自相关系数r1和二阶自相关系数r2为检验指标，模型模拟序列与实测序列各截口统计参数如图7、8 和图9所示。同时，为了便于分析，对于平稳序列的花园口站和白马寺站也采用TD模型进行了月径流模拟，其模拟序列的统计参数如图8 和图9所示。由图7、8 和图9 可知，3 个典型水文站中CEEMD-TD 模型模拟序列和实测序列各截口统计参数的变化趋势非常相近，由此可知，该模拟序列总体上均能较好地保持实测序列的主要统计特性。

图7 黑石关站月径流实测及各模拟序列统计特性对比图Fig.7 Comparison diagram of monthly runoff measured at Heishiguan Station and statistical characteristics of each simulated series

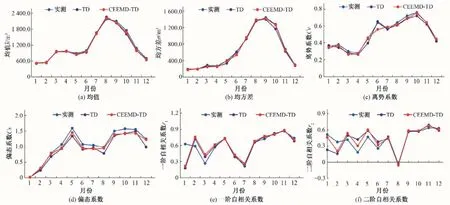
图8 花园口站月径流实测及各模拟序列统计特性对比图Fig.8 Comparison diagram of monthly runoff measured at huayuankou Station and statistical characteristics of each simulated series

统计各截口统计参数相对误差发现：3 个典型水文站中CEEMD-TD 模型模拟序列和实测序列的截口统计参数相对误差的绝对值均较小，其中黑石关站的均值、均方差σ、离势系数Cv和偏态系数Cs与月径流实测序列的截口统计参数的ARE均不超过10%，且均值的ARE 仅3.09%；花园口站和白马寺的均值的ARE分别为3.05%和3.9%。

与TD 模型的ARE对比分析发现，除了花园口站的一阶自相关系数r1高于TD模型1.89%和白马寺站的一阶自相关系数r1高于TD 模型4.24%外，其余CEEMD-TD 模型模拟序列的ARE均低于TD模型。因此CEEMD-TD 模型模拟序列总体上均能保持实测序列的主要统计特性，且优于TD模型。

3 结论

（1）本文结合典型解集（TD）模型，以河南省黄河流域3 个典型水文站为例，将对非平稳序列有较强的处理能力的互补式集合经验模态分解（CEEMD）法引入到径流随机模拟中，提出一种新的互补式集合经验模态分解-典型解集（CEEMD-TD）模型。通过模拟表明CEEMD-TD 模型能较好地模拟黄河流域3个典型水文站的月径流序列，解决典型解集（TD）模型仅适用于平稳序列的局限性。

（2）通过对各月径流序列截口统计参数来对模拟序列进行评价，结果表明：CEEMD-TD 模型模拟序列和实测序列的相对误差的绝对值均较小，且通过与TD 模型模型的模拟序列对比分析，表明在各典型水文站的模拟序列总体上均能较好地保持实测序列的主要统计特性。

（3）由于CEEMD-TD 模型是先模拟总量，再分解成分量，从而导致前一年最后分量与后一年第一分量的自相关结构不一致的问题，因此对于CEEMD-TD 模型在月径流的模拟有待后续进一步研究。□