一种基于奇偶次谐波分离的Nyquist折叠接收机

匡宏印，梅本春

（中国西南电子技术研究所，四川成都，610036）

0 引言

监视带宽是侦察接收机的重要指标之一，决定了其对未知信号的截获概率。在Nyquist采样理论的约束下，数字接收机的监视带宽受限于ADC器件的采样频率和量化位数，目前常用的带宽扩展方法是采用多通道方案。然而采用多通道ADC拼接合成大带宽方案会带来接收信道设计的复杂化和多通道相位同步难题，特别是当ADC的采样率提高到数GHz时，保证各通道的相位同步是极其严峻的挑战。

受压缩感知技术的启发，Fudge等人提出的一种全频带接收机架构，即Nyquist折叠接收机（NYFR），其原型架构如图1所示，基本原理是在数字采样前的混频过程中使用非均匀本振对接收信号进行模拟调制，将位于不同频段的信号下变频至ADC器件的奈奎斯特区域（Nyquist Zone，NZ)，然后经过低通滤波后进行ADC采样。Nyquist折叠接收机（NYFR）可被看做是对传统单频率本振超外差接收机的改进和扩展。本振中的非均匀分量通过不同的调制参数对不同频段的信号进行标记，使得后续可以通过特定的数字信号处理算法在完成调制参数估计后推算接收信号折叠前所在真实频段，该过程被称为奈奎斯特区域检测。结合折叠后的信号载频以及奈奎斯特区域检测结果可最终完成宽频段雷达信号的准确侦察接收[1]。Nyquist折叠接收机（NYFR）结构与一般压缩感知结构相比具有更明确的物理意义，并且与经典调制理论较为接近，后续数字信号处理较一般压缩感知更简易，是一种工程中较易实现的结构。并且该接收机在理论上可以用有限的采样频率实现全频带信号的接收，从而突破ADC器件的限制，实现超带宽接收机，在侦察接收机领域具备极高的研究应用价值。

图1 NYFR原型

国外Nyquist折叠接收机（NYFR）研究方面Ray M等人利用正交匹配追踪算法恢复原始信号，但运算量较大[3]。O.Odejide等人在Fudge研究基础上将小波分析算法于Nyquist折叠接收机（NYFR）的信号检测，降低了计算复杂度[4]。Ke Yu-long等人使用编码信号作为调制本振，以调制带宽固定但编码信息不同的调制本振分量划分奈奎斯特区域，扩展了监测带宽范围，但其基于伪魏格纳分布(PWVD)的参数估计算法在处理多分量信号时存在交叉项[5]。国内学者曾德国、仇兆炀等在接收机的结构及信号处理方面开展了研究，侧重点在信号处理理论，包括本振重构、NZ估计、参数估计等，工程应用面临的问题研究相对较少[6-7]。

虽然Nyquist折叠接收机（NYFR）理论上是全频带接收机，但在工程应用时，调制本振频率和调制带宽却限制了接收机的有效监视带宽。原型Nyquist折叠接收机（NYFR）存在2个工程应用问题，一是随着谐波次数不断增加，对应的本振带宽也会增加，达到一定限值后，相邻2个谐波间就发生频谱混叠，此时将不能进行NZ估计；二是输入信号如果位于2个谐波中间附近，由于2个谐波有一定的带宽，此时接收机的输出也会发生频谱混叠，影响后续的NZ估计。问题一限制了Nyquist折叠接收机（NYFR）的最大监视带宽，问题二导致接收机存在一定监视盲区，二者均在一定程度上限制了接收机应用。这两个问题如得到有效解决或者削弱则对Nyquist折叠接收机（NYFR）的工程化应用会有较高的价值。

1 奇偶次谐波分离原理及Nyquist折叠接收机架构

根据Fudge的原型推导[2]，有：

其中，p(t)为模板脉冲（如高斯等），sw为射频采样时钟角频率，θ(t)为调制相位。由式（1）可知，p~(t)中含有k次谐波，k= 0,1,......∞。

提高Nyquist折叠接收机（NYFR）有效监视带宽的常规途径包括提高sω或者降低θ´(t)（调制带宽），sω的上限是ADC器件的采样频率fADC，受限于当前器件水平，无法任意提高；θ´(t)也不能过小，否则信号处理模块无法分辨。在sω与θ´(t)确定的条件下，如果能提高调制本振谐波间的间隔，也可以达到监视带宽拓展的目的。

将式（1）进行如下展开，

式（2）即将p~(t)分成奇和偶次谐波2部分。

令：

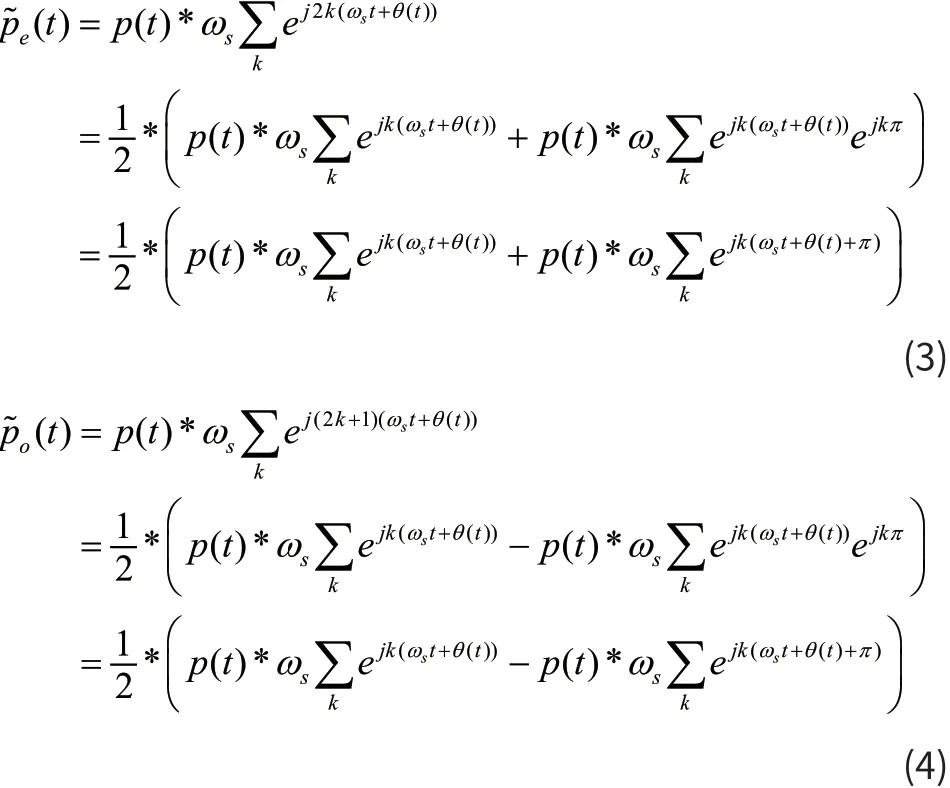
由式（3）和（4）可以看出，奇次项和偶次项可由原始采样脉冲与其相差180度的脉冲相加减得到，由此得到基于奇偶次谐波分离的Nyquist折叠接收机（NYFR）架构如图2所示，图中，ZCR表示上升沿过零，ZCF表示下降沿过零。将通过预选滤波器的信号序列x(t)分别使用调制本振的奇次项和偶次项进行折叠采样，再使用低通滤波器完成低通滤波处理，使用ADC进行均匀采样，将采样序列送入数字信号处理器件完成后续处理。

图2 奇偶次谐波NYFR

用奇次、偶次谐波支路对信号分别进行折叠采样，使得单个支路的相邻谐波间隔为2sω，与原型接收机相比，在相同的条件下谐波间的保护带宽扩大1倍，允许接收的信号频率就更高，从而拓展了对信号的有效侦收频谱范围。

2 仿真验证

Nyquist折叠接收机（NYFR）信号处理的关键步骤之一是对奈奎斯特区域(NZ) 进行估计，得到正确的NZ值，即可估计出输入信号的载频，进一步重构本振对信号进行解调恢复以进行后续的其他参数估计。NZ的估计方法有多种[1-2]，其中对折叠后的信号带宽进行估计是比较直接的方法。

为对比两种折叠接收机架构本振变化带来的差异，本文采用直接带宽估计方法，输入为简单脉冲信号（MP），仿真对比验证二者的差异。

2.1 特定频点混叠情况对比

使用MATLAB软件产生信号进行仿真验证，仿真条件如下：

(1)仿真频率：fsim= 60GHz 该频率设置为等效观察ADC采样前的模拟信号；

(2)输入信号频率：2.53GHz，简单脉冲，数据长度：100000点；

(3)不加采样前级低通滤波器（为观察混叠情况）；

(4)采用LFM本振，fs=1GHz，调频率K=6e13Hz/s，带宽：100MHz（该带宽设置偏大，便于观察混叠，工程应用时需综合采样率、系统侦收带宽考虑）；

(5)fADC= 2GHz 。

仿真结果，如图3所示。

图3(a)为射频采样脉冲频谱，蓝色为原型架构的本振频谱，包含了所有谐波分量，可看出谐波次数增大，其自身带宽越大，谐波间的间隔就越小；红色和黄色是新架构的偶次和奇次支路的本振频谱，从仿真验证了架构奇偶分离的正确性。

图3(b)是本振对输入信号进行折叠后的频谱，蓝色为原型架构的输出xs(t)的频谱，可以看出2次谐波（2GHz）和3次谐波（3GHz）的输出发生了频谱混叠；红色、黄色是新架构偶次和奇次谐波支路的输出xe(t),xo(t)的频谱，偶次谐波2GHz与奇次谐波3GHz的混叠输出已分开，可以可分别进行带宽估计以得到输入信号的频率。

图3 特定频点仿真结果

仿真结果表明，新架构可以解决原型接收机在输入信号在某些频点时发生频谱混叠的问题，减小了接收机的监视盲区。

2.2 侦收频率范围对比

使用MATLAB软件产生信号进行仿真验证，仿真条件如下：

(1)仿真频率：fsim= 60GHz 该频率设置为等效观察ADC采样前的模拟信号；

(2)输入信号频率：5.5 GHz,11.5GHz，简单脉冲，数据长度：100000点；

(3)不加采样前级低通滤波器（为观察混叠情况）；

(4)采用LFM本振，fs=1GHz，调频率K=6e13Hz/s，带宽：100MHz（该带宽设置偏大，便于观察混叠，工程应用时需综合采样率、系统侦收带宽考虑）；

(5)fADC= 2GHz 。

仿真结果，如图4所示。

图4(a)为原型接收机输出xs(t)的频谱，在输入为5.5GHz时，输出在±1GHz（fADC= 2GHz）范围内谐波混频输出已发生混叠，无法分辨，不能正确估计NZ值。

图4(b)为新架构的折叠输出，对于5.5GHz输入，在±1GHz范围内可明显分辨信号；增大信号到11.5GHz，亦可明显区分谐波的混频结果，有效频率范围可扩展近1倍。

图4 频率范围仿真结果

2.3 NZ估计正确率对比

仿真条件：使用MATLAB软件产生信号进行仿真验证，仿真条件如下：

(1)仿 真 频 率：fsim= 60GHz 该频率设置为等效观察ADC采样前的模拟信号；

(2)输入信号频率：2.3GHz，简单脉冲，数据长度：100000点；

(3)加高期白噪声，SNR＝4 dB，6 dB，8 dB，10dB，每个SNR下做蒙特卡洛试验100次；

(4)不加采样前级低通滤波器（为观察混叠情况）；

(5)采用LFM本振，fs=1GHz，调频率K=6e13Hz/s，带宽：100MHz（该带宽设置偏大，便于观察混叠，工程应用时需综合采样率、系统侦收带宽考虑）；

(6)fADC= 2GHz 。

仿真结果如图5所示，奈奎斯特区域估计正确率如表1所示。

图5 不同SNR的下NZ估计对比结果

表1 NZ估计正确率

输入信号为2.3GHz，对于原型架构和偶次谐波支路，奈奎斯特区域（NZ）估计正确结果是1，对于奇次谐波支路，奈奎斯特区域（NZ）估计正确结果是2。在低信噪比条件下，偶次谐波支路的正确率明显高于其他两种结果，奇次谐波支路优于原型架构（奇次比偶次差的原因：对于2.3GHz输入信号，奇次本振（3GHz）比偶次本振（2GHz）的功率低，等效SNR低）。可见，改进架构可以提升接收机灵敏度。

3 结论

针对Nyquist折叠接收机（NYFR）原型架构相邻谐波对信号折叠出现混叠，导致出现监视盲区和监视带宽降低问题，本文提出了一种基于奇偶次谐波分离的Nyquist折叠接收机（NYFR）架构，可解决原型架构的问题，同时拓展了信号侦收频率范围，提升接收机灵敏度。该架构在ADC采样率限制条件下，可提升Nyquist折叠接收机（NYFR）系统适应性，因此该架构具有较强的应用价值。此架构解决了谐波间的混叠问题，但对于输入的实信号，由于存在正负频，所以当谐波次数增加，折叠后正负频混叠问题也会突出，后续继续研究解决此问题的方法，以进一步提升基于奇偶次谐波分离的Nyquist折叠接收机（NYFR）适用性。