基于Workbench的油罐车流固耦合系统谐响应分析

王明慧, 党鹏飞

(沈阳化工大学 机械与动力工程学院, 辽宁 沈阳 110142)

公路运输在我国国民经济和综合运输网络中具有其他运输方式难以替代的作用,但是存在单车油罐在受到强烈的外载荷作用时液体晃动十分严重的问题.在外界激励作用下,载液罐体内液体对罐体结构产生的晃动冲击能够造成罐体结构的严重损坏.同时在实际工程中,罐体结构倾向于采用具有薄壁、轻质和高强等特点的材料,因此晃动液体对结构的耦合冲击成为非常重要的问题.郑州大学张庆华等[1]基于ANSYS APDL对油罐流固耦合系统进行模态分析,得出流体大大降低了系统固有频率的结论;吉林大学李显生等[2]利用Fluid对油罐内液体进行分析,得出充液比和外部激励时液体冲击的关键因素.向韬等[3]运用ADINA对油罐车和流固耦合系统分析,发现各工况下油罐车最大应力都位于罐体纵梁前端与车架纵梁接触的部位,应力较大区域集中在与前后钢板弹簧相连接的车架纵梁和对应横梁上;薛杰等[4]使用流固耦合法对充液容器流固耦合模态仿真,最终得到了流体对于结构模态特性影响的变化规律.结合上述研究,本文采用ANSYS Workbench/Fluent对油罐流固耦合系统施加0.981 m/s2(0.1g)加速度基础激励进行谐响应分析,探究在不同充液比的情况下油罐应力的变化.

1 理论基础

1.1 流固耦合理论基础

流体流动遵循物理守恒定律.基本的守恒定律包括质量守恒定律、动量守恒定律.对于一般的可压缩牛顿流体,守恒定律可描述为：

质量守恒方程：

(1)

动量守恒方程：

(2)

式中：t表示时间;ff是体积力矢量;ρf是流体密度;v是流体速度矢量;τf是剪切力张量,可表示为

τf=(-p+μ∇·v)I+2μe.

(3)

式中：p是流体压力;μ是动力黏度;e是速度应力张量.

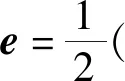
(4)

固体的守恒方程可由牛顿第二定律导出[5].

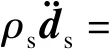
(5)

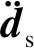
1.2 谐响应理论基础

谐响应分析用于确定结构在已知频率和幅值的正弦载荷作用下的稳态响应.该技术只作用于稳态受迫振动,不考虑结构在激振开始时的瞬态振动.简谐载荷下受迫振动的运动微分方程为[6]

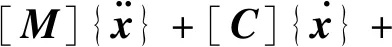
[K]{x}={f(t)}sinωt.

(6)

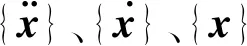
{x}={A}sin(ωt+φ0).

(7)

式中：{A}为位移幅值向量;φ0为位移响应滞后激励力的相位角.把式(7)代入式(6)可得谐响应的运动方程

[A](-ω2[M]+ω[C]+[K])sin(ωt+

φ0)={f(t)}sinωt.

(8)

ANSYS中提供了两种常用的谐响应分析方法,分别是Full(完全法)和MSUP(模态叠加法).完全法不仅易于使用,还允许定义各种类型的载荷,具有普遍性.笔者采用完全法进行谐响应分析.

2 谐响应分析

油罐罐体组成固体域,罐体内的流体组成流体域.模型轴线垂直,几何对称,罐体尺寸见图1[7].罐体材料为普通碳素结构钢Q235,壁厚10 mm,密度为7800 kg/m3,杨氏模量为2.06×1011Pa,泊松比为0.3;流体材料为Gasoil-liquid,密度为830 kg/m3,黏度为3.32×10-3Pa·s.

图1 G60罐体简图Fig.1 Installation diagram of G60tank

实体模型如图2所示.采用分离法对流固耦合系统进行分析,流体分析和罐体分析可以不同步进行.在Workbench中打开Fluid Flow(Fluent)模块,先进行流体域求解.把上述罐体模型导入Geometry中,然后点击Mesh,在Mesh中选择抑制固体域,再划分网格,把画好的网格导入Fluid中,点击Setup进入Fluid软件.笔者研究的是不同充液率罐体,因此选择VOF多相流模型.罐内的相为气液混合,分别选择空气、Gasoil-liquid材料作为第一、第二相,设置压力求解器,湍流模型为k-epsilon(2eqn)模型,设置罐内参考压强为一个标准大气压,z轴的负方向为重力方向,大小为9.81 m/s2,施加侧向加速度(y轴方向),大小为0.981 m/s2(0.1g).其他设置保持默认,进行求解,结果见图3～图6.

图2 罐体三维模型Fig.2 Three-dimensional model of tank

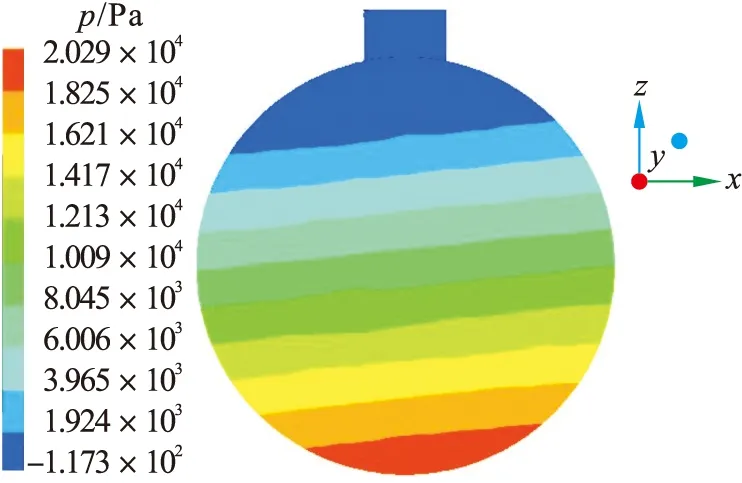
图3 充液率90%流体压力图Fig.3 90% fluid pressure diagram filled with liquid

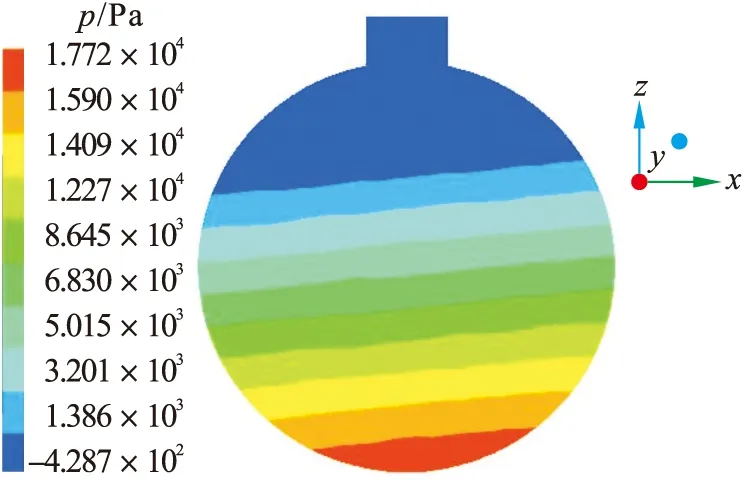
图4 充液率80%流体压力图Fig.4 80% fluid pressure diagram filled with liquid

图5 充液率70%流体压力图Fig.5 70% fluid pressure diagram filled with liquid

图6 充液率60%流体压力图Fig.6 60% fluid pressure diagramfilled with liquid

接下来进行固体域的求解.把模型导入Static Structural中的Geometry中,双击Mesh,在Mesh中选择抑制流体域,划分网格.双击打开Setup进入ANSYS Mechanical Enterprise界面,设置流固耦合面,把Fluid中计算的结果以压力的形式导入进来,在两个支架一端施加全约束,另一端横向自由,其他方向都固定,设置重力加速度,进行求解.打开Harmonic Response进行谐响应分析.设置频率范围0～60 Hz,分为10个区间,阻尼比为0.2.施加一个0.981 m/s2(0.1g)的加速度基础激励,进行求解.分别考虑罐体内储存不同深度的自由液面的汽油,采用ANSYS Workbench有限元软件来计算不同深度的液面对油罐的影响,结果见图7～图10.

图7 充液率90%的应力图Fig.7 Stress diagram with 90% liquid filling rate

图8 充液率80%的应力图Fig.8 Stress diagram with 80% liquid filling rate

图9 充液率70%的应力图Fig.9 Stress diagram with 70% liquid filling rate

图10 充液率60%的应力图Fig.10 Stress diagram with 60% liquid filling rate

应力最大处在油罐与全固定支架的接触面附近.根据第四强度理论,应力最大值点的位置以及应力最大值处充液率与频率对应力的影响见表1.

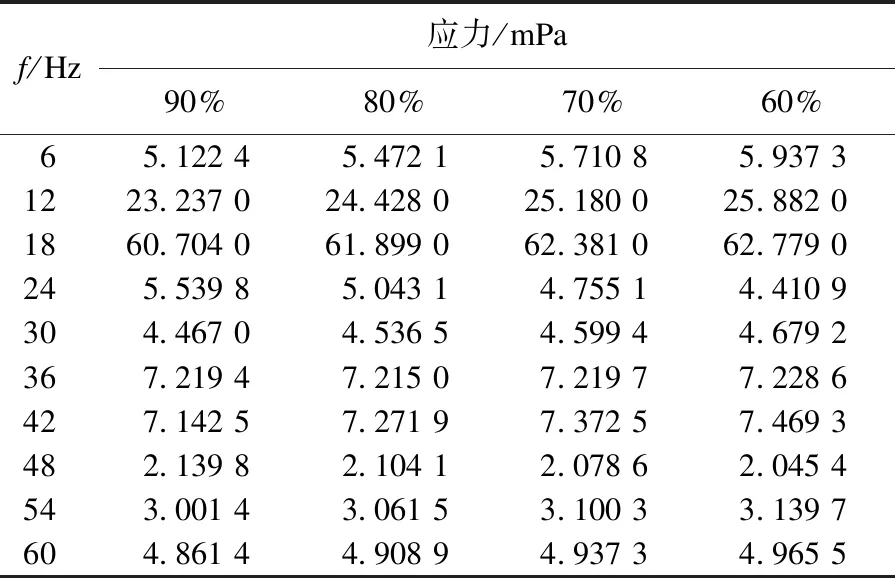
表1 不同充液率各频率下的应力Table 1 Stresses under different filling rates and frequencies

3 结 论

利用ANSYS Workbench/Fluid对油罐车的油罐流固耦合系统进行了谐响应分析,得到如下结论：

(1) 通过应力最大值和频率的关系可以得出：不同充液率下的油罐流固耦合系统在相同的加速度基础激励的作用下,随着充液率的增加,在相同频率下应力值逐渐减少.

(2) 对油罐施加0.981 m/s2(0.1g)的加速度基础激励,可以发现油罐的应力最大值在全约束支架处附近.