液体燃料横向射流雾化数值模拟研究

刘晶晶，叶桃红

(中国科学技术大学 热科学与能源工程系，安徽 合肥 230027)

液体燃料横向射流是亚燃和超燃冲压发动机中一种常见且高效的燃料进入方式[1]。液体燃料雾化过程对后续的蒸发、混合和燃烧过程有着重要影响。在液体燃料横向射流雾化过程中，气体韦伯数和射流动量通量比是影响初次雾化不稳定性和射流穿透深度的重要参数。为了揭示横向射流雾化破碎机理，许多学者对不同条件下的液体燃料横向射流雾化进行了实验研究[2-4]。尽管对喷雾的实验研究取得了一定的进展，但是在航空航天应用中，高温高压环境使得实验研究非常困难和昂贵，所以数值模拟得到了发展。

目前液体射流雾化的模拟方法主要可以分为三大类：欧拉框架，欧拉-拉格朗日框架和混合欧拉-拉格朗日框架。第一类方法通过解析相界面直接求解射流破碎过程，常用的界面捕捉方法为流体体积(VOF)方法[5-6]，水平集(level-set，简称LS)[7]方法以及两者的耦合(CLSVOF)[8-10]方法。但是这种方法要求网格极为精细以捕捉到液体表面产生液滴的过程，需要的计算量非常大。第二类方法气相被看作连续相在欧拉框架下求解，液体射流被假设为与喷嘴直径相同的Blobs大液滴在拉格朗日框架下求解，此种方法常常将二次破碎模型直接扩展到初次破碎的求解中，典型的二次破碎模型有WAVE模型[11]，KH-RT(Kelvin-Helmholtz Rayleigh-Taylor)模型[12]，TAB(Taylor Analogy Breakup)模型[13]等，这种方法大大减小了计算量，但是忽略了真实的射流是连续的流体。第三类方法指在欧拉框架下求解连续的气液相，在拉格朗日框架下求解离散相液滴，初次破碎过程由模型进行模化，并将该过程生成的液滴从Eulerian场中转化到Lagrangian场中。此方法对气液相界面直接求解，既可以较为准确地求解液体射流和气流之间的相互作用，又可以减少计算量。

本文基于混合欧拉-拉格朗日框架，采用VOF耦合Lagrangian算法对Lubarsky等人[4]实验中航空煤油(Jet A)喷入横向气流中的雾化过程进行了大涡模拟研究，重点分析了射流穿透深度、液滴平均直径和速度分布以及气相平均流场结构。

1 数学物理模型

1.1 欧拉框架下的控制方程

大涡模拟的基本思路是利用空间滤波方法消除湍流中起耗散作用的小尺度脉动，并采用亚格子模型将其封闭，同时直接求解包含所有湍动能的大尺度脉动。根据流体连续性假设，气液两相连续流体大尺度运动的控制方程如下：

1)质量守恒方程

本文采取低马赫数下不可压缩假设，质量守恒方程为

(1)

2)动量守恒方程

(2)

(3)

本文采用Smagorinsky涡黏模型对亚格子应力进行模化，如式(4)所示：

(4)

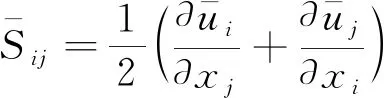
(5)

式中：Δ为过滤尺度；Cs为Smagorinsky常数。Su,i为连续相和离散相之间的动量交换源项。

(6)

式中：nd为一个液滴包裹(parcel)的数密度；FD,i为液滴上的拖曳力；Sσ为表面张力在动量方程中产生的源项Sσ=σkα，采用连续表面张力模型[14]模化。

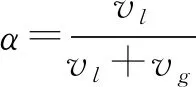
混合连续流体的密度和动力黏度根据相体积分数加权计算，下标g代表气相，下标l代表液相：

ρ=(1-α)ρg+αρl

(7)

μ=(1-α)μg+αμl

(8)

体积分数输运方程如下：

(9)

式中：Sα是与Eulerian/Lagrangian框架转化有关的源项，计算方法为一个网格内的液相体积分数与时间步长Δt的比值：

(10)

1.2 拉格朗日框架下的控制方程

离散相液滴运动规律遵循牛顿第二定律；采用双向耦合，即除了考虑气流对液滴的影响，还将考虑液滴对气流的影响，通过动量方程来描述。液滴的位置和速度通过以下方程得到：

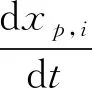
(11)

(12)

式中：下标p代表液滴；m，u和x分别为其质量(kg)，速度(m/s)和位置(m)；下标i代表矢量的三个分量；FG,i为重力和浮力的合力；FD,i为拖曳力，由式(12)计算：

(13)

式中：Dp为液滴直径，mm；ρg为气相密度，kg/m3；ug,i为在欧拉场中位置的气相速度；CD为阻力系数，采用Schiller-Naumann阻力模型[15]计算。

液滴的二次破碎由Reitz Diwakar[16]二次模型模化，液滴的碰撞和融合由Nordin的碰撞算法[17]计算。

1.3 欧拉和拉格朗日框架之间的转化

本文采用Martin等人[18]给出的算法将欧拉场中射流初次破碎产生的液团转化到拉格朗日场中的离散液滴进行追踪。该算法首先采用网格标记关联法对欧拉场中的液团进行识别，规定一个液相体积分数临界值αt(10-2数量级)，大于该临界值的网格将被标记为液相网格，否则被标记为气相网格，接下来该算法循环遍历所有网格，并将每个液相网格都标记为唯一的网格ID。然后，对于标记过的所有液相网格，找到它们的相邻网格，将它们的网格ID改为相邻网格中的最小ID，这样在欧拉场中具有相同ID的液相网格就构成了一个液团。

计算识别到的所有欧拉场中液团的体积、位置、速度和直径：

(14)

根据计算得到的液团参数，设置以下准则：

(1)直径小于某一临界值dmax，一般为网格尺寸的4～6倍，因为直径较大时，液团还会发生形变，直径小于网格尺寸的4～6倍时，采用VOF方法已经不能准确描述液团的形状和动力学特性。

如果满足以上准则，欧拉场的液团就会被转化为拉格朗日离散液滴注入计算域，同时将液团从欧拉场中删除(即α=0)。

1.4 几何模型与算例设置

根据Lubarsky等人的实验装置，本文数值模拟采用的计算域及几何结构示意图如图1所示。燃料入射孔直径为0.457 mm，燃料管道长度L=10D，位于空气入口下游5 mm中心线上，空气入口截面为46 mm×30 mm，坐标轴原点位于射流出口圆心位置处，计算域总长71.2 mm。

图1 计算域几何结构示意图

采用openfoam平台网格工具snappyHexMesh对计算域进行网格划分，计算时对气液相界面采用动态自适应加密，最小网格尺度为0.03 mm。

根据实验条件，表1给出了本文开展的四个仿真算例的详细参数，其中横向来流为温度555 K的预热空气，腔内压强维持在4atm。Case1-3的射流动量通量比均为40，气体韦伯数分别为33、470和800。此外，为了分析不同射流动量通量比下的雾化特性，又设置4#的射流动量通量比为10，气体韦伯数为470。表2为燃料Jet A的物性参数。

表1 不同算例的详细参数信息

表2 Jet A航空煤油的物性参数

1.5 数值计算方法与边界条件

采用有限体积方法离散控制方程，相体积分数方程的对流项离散格式为Gauss vanLeer格式，动量方程中的对流项为二阶Gauss LUST grad(U)格式离散，其余方程对流项为高斯迎风(Gauss upwind)格式，其他项(面法向梯度，梯度项，拉普拉斯项等)采用高斯线性(Gauss linear)格式。采用PIMPLE算法进行压力速度的耦合求解，采用动态调整时间步，保持库朗数Co<1。

对于初始场和边界条件，给定来流空气入口参数作为初始条件，空气和燃料入口边界条件均为均匀边界条件加上4%的湍流脉动，壁面边界采用无滑移条件，计算域出口采用压力出口边界，假设出口处各个物理量零梯度。

2 计算结果与分析

2.1 射流穿透深度

本文的模拟计算采用高温高压条件，选用的参考实验未给出射流穿透深度，故选择Li Lin等人[19]和Yogish Gopala等[20]提出的高温高压条件下的射流穿透深度经验关系式，与模拟结果进行对比。Li Lin提出的射流穿透深度经验关系式为

(14)

Yogish Gopala等人提出的射流穿透深度经验关系式为

y/dj=1.393q0.482log(1+1.267x/dj)

(15)

图2为1#-4#模拟得到的射流穿透深度与上述两个经验关系式的对比。由图2可知，四个算例模拟得到的射流穿透深度均与两个经验关系式对比较好，且随着射流动量通量比增加，射流穿透深度明显增加。对于相同射流动量通量比的1#-3#，1#在X/D>40时射流穿透深度较大于2#和3#，这是由于1#中来流空气和射流雷诺数较小，导致了较小的湍流作用和空气动量，射流破碎程度减弱，射流穿透深度增加。由此看来，尽管射流穿透深度主要受动量通量比的影响，但是由于来流空气和液体射流的雷诺数影响着液滴破碎、分散和混合，因而会影响射流穿透深度[21]。此外，在距离射流出口较远的下游，模拟的射流穿透深度略高于经验关系式。

图2 1#～4#射流穿透深度与经验关系式的对比

2.2 液滴平均直径和速度分布

图3为1#在x=30 mm截面处统计结果与实验结果的对比，模拟结果与实验基本保持一致，但液滴穿透深度未达到实验值，由于模拟结果在高射流穿透深度处只存在非常少的大液滴，不具备统计意义，故这里将其忽略。从图3(a)和图3(b)可以看出，随着喷雾穿透深度增加，液滴索特平均直径(SMD)和算术平均直径(AMD)均增加。在较高穿透深度处，液滴SMD和AMD均大于90 μm，表明射流顶部发生了柱破碎现象，该机制生成的液滴尺寸较大；在低穿透深度处，液滴的平均直径在20～50 μm，表明射流柱初次破碎生成液滴的机制为剪切破碎，该机制生成的液滴尺寸较小；综上可知Weg=33时射流初次破碎机制为多模式破碎机制，即包含柱破碎和剪切破碎。在图3(d)中，壁面附近液滴y方向速度分量Vy为负值，说明靠近壁面处存在涡旋结构[4]。

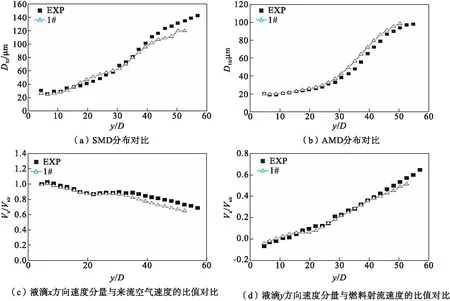
图3 1#在x=30 mm截面处统计结果与实验结果的对比

图4为1#～4#在x=30 mm截面处统计结果之间的相互对比，对于射流动量通量比相同(q=40)的1#～3#，三个算例的液滴平均直径分布和速度分布趋势较为一致，4#的穿透深度明显低于1#～3#，与2.1节的分析一致。从图4(a)和图4(b)可以看出，2#～4#的SMD和AMD值均在10～60 μm，表明了在较高气体韦伯数时，空气动力作用较强，破碎生成的液滴直径较小，液滴的形成机制为剪切破碎。在靠近射流壁面处，液滴平均直径较小，这些小液滴在空气动力的作用下从液柱表面剥离[3]，随着距壁面距离的增加，液滴平均直径逐渐增大。由于4#的喷雾穿透深度较小，在同一深度，4#的平均直径较大于1#～3#，对于1#～3#，随着气体韦伯数增大，同一深度的液滴平均直径减小。图4(c)中，y/D在15～20附近时，存在一个液滴平均速度较小的区域，这个区域为尾流区，主要是由于液柱表面波与空气的动量交换形成的，尾流区内的液滴会失去部分的横向动量[3]。此外，在同一深度处，2#～3#的Vx/Vair值大于4#，这主要是由于液滴直径的不同导致的，当剪切破碎形成的液滴较小时，易被周围气体加速，故沿x方向的速度较大。但是这个规律却不适用于1#，1#的平均直径较2#、3#大，但1#的Vx/Vair值反而大于2#～3#，这主要是由于液滴形成机制的不同导致的[4]，1#为多模式破碎机制，2#～4#为剪切破碎机制。图4(d)中，在射流壁面附近均出现负的y速度，说明1#～4#壁面附近均存在涡旋结构，靠近壁面处的小液滴跟随涡旋结构运动，一部分向着壁面方向即-y方向运动。

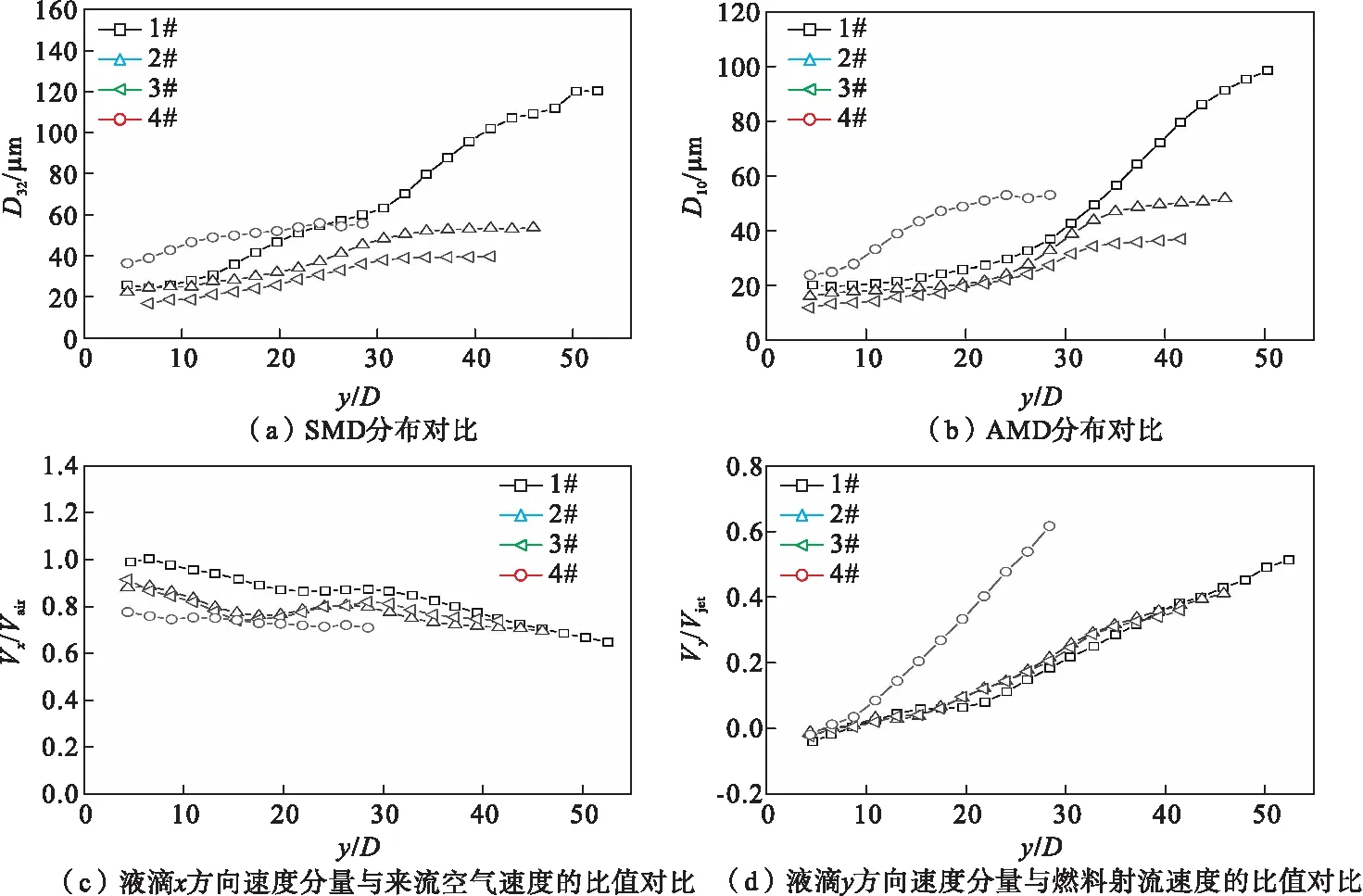
图4 1#～4#在x=30 mm截面处统计结果相互对比

2.3 气相平均流场结构

图5示出了液柱与周围空气相互作用的流线图，流线由气体涡量的y方向分量进行着色，观察到两个算例在射流柱下游均产生了对称的回流区结构，2#中回流区尺度大于4#，这是由于2#的射流动量通量比较4#大，射流柱较高，对来流空气的阻碍作用更强；除此之外，在靠近射流柱底部的下游处，来流空气绕过液柱，2#中在靠近壁面处形成了尺度相对较小的回流区，而在4#中并没有观察到，这是因为4#中较大尺度的回流区产生的涡结构位置较靠近壁面，从而导致涡旋与壁面相互作用，阻碍了壁面附近小尺度回流区的产生。

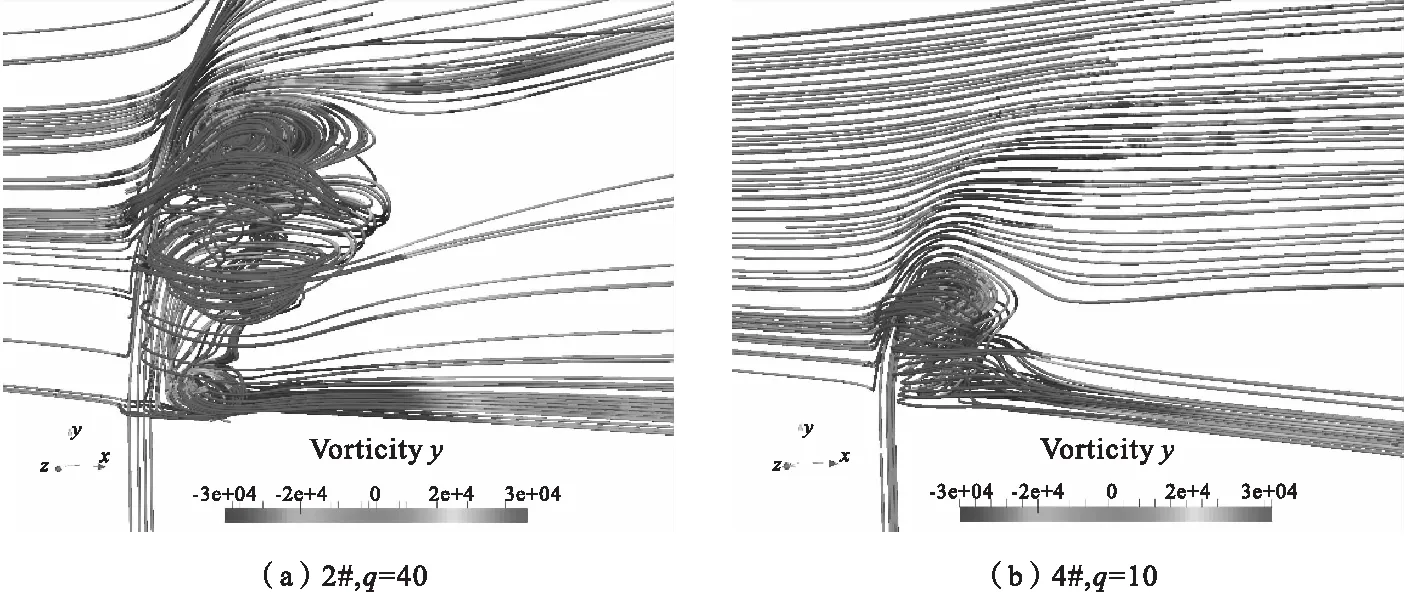
图5 液体射流周围的空气平均流线图

3 结 论

采用流体体积耦合拉格朗日方法对航空煤油(Jet A)喷入横向气流中的雾化特性和流场结构进行了大涡模拟(LES)研究，得到结论如下：

(1)不同气体韦伯数Weg(分别为33、470和800)和不同射流动量通量比q(分别为10和40)下的射流穿透深度均与经验关系式对比良好，且随射流动量通量比增加，射流穿透深度增加。尽管射流穿透深度主要受动量通量比的影响，但是若来流空气和射流射流雷诺数较大，则会增强液滴的破碎，分散和混合过程，导致液滴穿透深度降低。

(2)通过对液滴平均直径和速度分布的分析，气体韦伯数为33的模拟结果与实验结果较为吻合，同时发现气体韦伯数较小时(Weg为33)，射流初次破碎机制多模式破碎；气体韦伯数较大时(Weg分别为470和800)，射流初次破碎机制为剪切破碎。

(3)在射流柱下游区域，气相流场中存在回流区结构。