采用黏弹性人工边界时显式算法稳定性条件*
2022-04-11刘晶波李述涛
刘晶波,宝 鑫,李述涛,2,王 菲,3
(1. 清华大学土木工程系,北京 100084;2. 军事科学院国防工程研究院,北京 100036;3. 陆军工程大学国防工程学院,江苏 南京 210007)
无限介质的波动辐射效应是波动数值模拟中需要考虑的关键问题,人工边界技术是处理此类问题最常用的技术手段。该方法在无限或半无限介质中截取有限的近场计算域,并在截断边界处施加人工边界条件,以吸收计算域内产生的外行波动。由于采用不同的数学、物理或力学原理,常用的人工边界技术可分为透射边界、黏性边界、黏弹性边界、边界元和完美匹配层等。其中,在黏弹性人工边界技术中,将介质中单侧波动的偏微分方程转化为施加于截断边界上的应力边界条件,并且等效为空间解耦的力学系统,物理意义清晰、实用性强,且具有较好的模拟精度和良好的鲁棒性。近年来,已被研究人员集成于Marc、LS-DYNA、ANSYS、ADINA、Nastran、ABAQUS等通用有限元软件,并应用于大坝、桥梁、核工程、隧道和地铁车站等建构筑物与基础的动力相互作用分析及工程场地的动力响应计算,取得了合理准确的计算结果。
采用显式时域逐步积分算法对含有黏弹性人工边界的整体模型进行计算分析时,受黏弹性人工边界阻尼、刚度等的影响,人工边界区的稳定性需比内部计算域的稳定性条件更严格。目前,尚无明确、实用的考虑黏弹性人工边界影响时显式时域逐步积分算法稳定性的判别准则,难以确定合理的数值积分时间步长,这一定程度限制了黏弹性人工边界在显式动力分析中的应用。与隐式算法相比,显式动力计算方法不需要求解耦联方程组,计算工作量较小、计算效率较高,在大规模复杂系统的动力分析尤其爆炸问题数值模拟中应用广泛。鉴于此,有必要对使用黏弹性人工边界时显式时域逐步积分算法的稳定性开展研究工作,以促进黏弹性人工边界在大规模显式动力分析中的应用。
本文中,针对含黏弹性人工边界的数值模型在显式算法中的稳定性问题,利用基于局部子系统的数值稳定性分析方法,给出可代表整体模型局部特征的不同边界子系统的稳定性条件解析解,比较分析不同计算区域的稳定性条件及其影响因素,给出整体模型在显式动力计算中的统一稳定性判别准则和简化实用计算方法。
1 黏弹性人工边界模型与参数设置
黏弹性人工边界由在截断边界处设置的空间解耦的弹簧-阻尼器构成,如图1 所示。
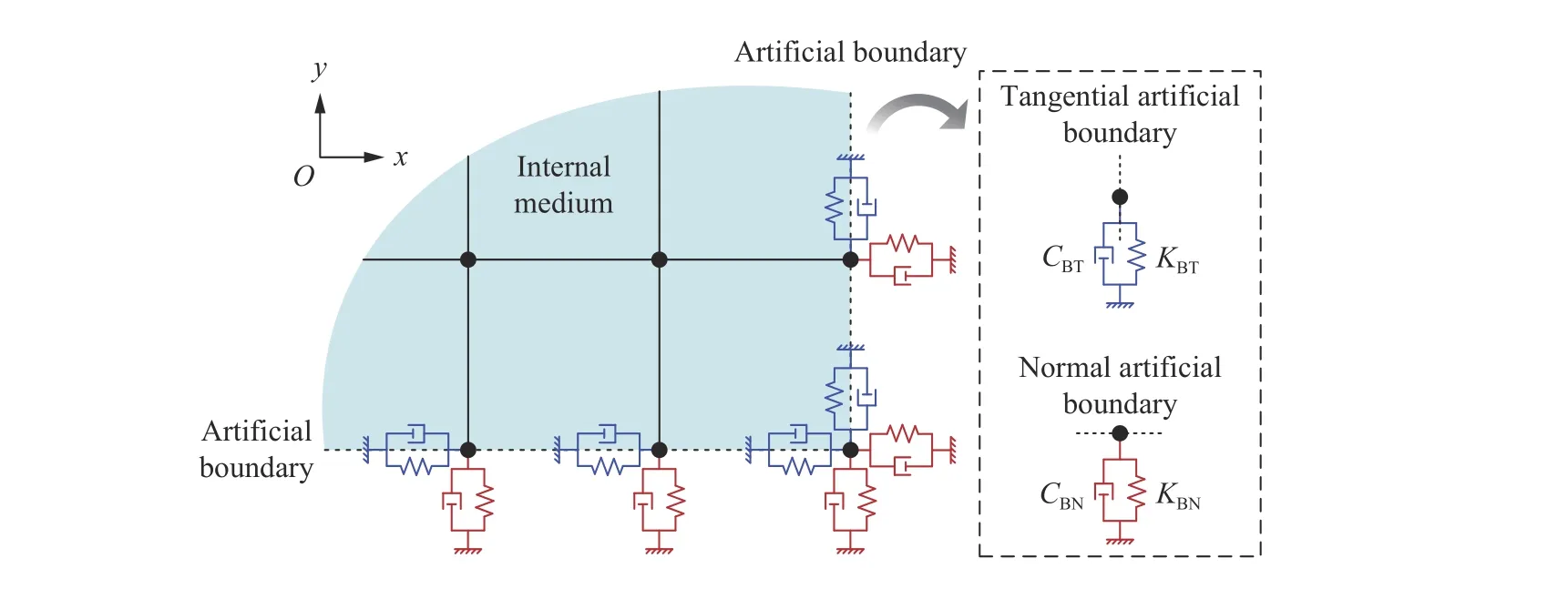
图1 黏弹性人工边界Fig. 1 Schematic diagram of viscoelastic artificial boundaries
二维情况下,黏弹性人工边界等效物理系统的弹簧刚度和阻尼系数分别为:


表1 二维黏弹性人工边界参数的数据[23]Table 1 The values of two-dimensional viscoelastic artificial boundary coefficients[23]
2 采用黏弹性人工边界时显式算法的稳定性分析方法
2.1 基于局部子系统的数值积分稳定性分析方法
数值稳定性是制约显式动力计算时间步长的主要因素,以往针对含人工边界条件的计算系统的稳定性研究,多基于整体模型或由若干排(列)节点构成的复杂节点系统,通过数值方法判断其稳定性。因未能给出解析形式的人工边界稳定性判别准则,此类方法的实用性仍有所欠缺。李述涛等总结和归纳了现有离散模型数值积分稳定性研究工作,得出以下结论:数值积分算法的稳定性由计算模型的最高阶频率即系统的截止频率控制;截止频率对应的振型一般呈现局部节点系相邻节点交错振动的模态,二维平面应变情况下,其振动形式如图2 所示。
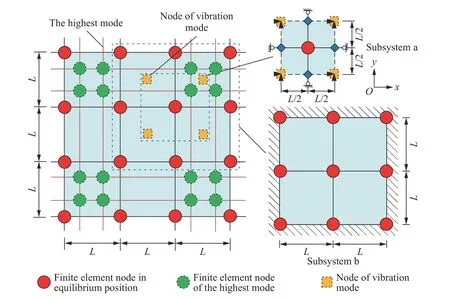
图2 基于局部子系统的稳定性分析Fig. 2 Stability analysis based on local subsystems
在上述基础上,李述涛等提出了一种利用局部子系统估算整体有限元模型数值稳定性的方法。根据该方法,对于任意整体有限元模型,如能较准确地判断其最高阶振型,则可利用振型节点的空间分布规律,截取由相邻振型节点包围的最小局部子系统(见图2 中的子系统a)。对该子系统的边界节点施加与整体模型最高阶振型一致的约束条件,并进行稳定性分析,获得的局部子系统稳定性条件即为整体模型的稳定性条件。而对于不能准确判断整体模型最高阶振型的情况,可选取由相邻单元构成的最小子系统(见图2 中的子系统b)。对该子系统的全部边界节点施加固定约束,分析所有b 型局部子系统的稳定性条件,其下限值为整体有限元模型稳定性条件的上限逼近。
基于局部子系统的稳定性分析方法,提供了一种从理论上估算含人工边界的复杂离散系统数值稳定性的技术手段。对于整体模型的内部计算域,可以采用子系统a 直接获稳定性条件,而对于边界区域,由于人工边界的影响,难以准确判断最高阶振型,无法从整体计算模型中分割出子系统a,此时可以采用b 型子系统进行稳定性分析。
2.2 基于传递矩阵谱半径的稳定性判别方法
稳定性条件因所采用的数值积分方法而异,为解决实际工程应用中黏弹性人工边界的稳定性问题,以在通用有限元软件中应用较广泛的蛙跳格式中心差分时域逐步积分算法为基础,分析含黏弹性人工边界的整体计算模型的数值稳定性。对于其他显式时域逐步积分算法,采用相似的步骤即可得到对应的稳定性条件。

数值积分方法的稳定性仅与积分格式、时空离散步长和计算系统的力学参数有关,而与外力向量无关。如满足以下条件,则积分格式是稳定的:(1) ρ() ≤ 1,其中ρ()为传递矩阵的谱半径,即ρ() =max|λ|,λ为传递矩阵的第个特征值,对于本文分析的二维情况,=1~4;(2) 如具有多重特征值,则该特征值的模小于1。
结合以上理论与方法,可将黏弹性人工边界在显式时域逐步积分算法中的稳定性分析分解为3 个步骤:(1)选取能体现整体有限元模型不同局部特征的子系统;(2)建立各子系统的运动方程,结合时域逐步积分算法推导传递矩阵,并求解谱半径;(3)根据谱半径的模小于等于1 的限制条件求解各子系统的稳定性条件,比较后选取最严格的稳定性条件作为整体模型最大稳定积分时间步长的上限估计。
另外,在满足了离散模型动力计算的稳定性条件下,为进一步满足精度要求,离散化网格的尺寸Δ需满足以下条件:

式中:λ为离散网格中波动传播的最短波长,为介质中的最小波速,为波动问题数值模拟的截止频率。
3 采用黏弹性人工边界时显式算法的稳定性分析
下面,针对二维情况,分析采用黏弹性人工边界时显式时域逐步积分算法的稳定性。由于稳定性条件与计算系统的单元尺寸和物理特性密切相关,为不失一般性,在数值算法的稳定性分析中通常采用规则几何模型、均一介质和均匀离散网格进行建模分析。对于不规则网格或非均匀介质,可根据有限元网格的最小尺寸及不同区域的介质材料参数,采用本文方法分别计算稳定性条件,并选取其下限值作为最大积分时间步长的选取依据。
二维半无限空间近场有限元模型如图3(a)所示,不考虑介质阻尼,内部均匀介质在中心差分算法中的稳定性条件为:

当采用黏弹性人工边界时,因难以确定人工边界区的最高阶振型,应采用b 型子系统进行稳定性分析。此时,根据截取位置的不同,人工边界区的b 型局部子系统可分为侧边(底边)子系统和角点子系统,如图3(a)所示。
为建立局部子系统的运动方程,先给出规则二维平面应变等参数单元(见图3(b))的刚度矩阵:

图3 二维半无限空间近场有限元模型及二维平面应变单元Fig. 3 Two-dimensional semi-infinite near-field finite element model and two-dimensional plane strain element

式中:为8×8 型的单位矩阵。
3.1 侧边子系统的稳定性条件
在图3(a)所示的侧边子系统中,仅节点1 为自由节点,其余节点均施加了固定约束。利用黏弹性人工边界物理参数(式(1))及平面应变单元的刚度和质量矩阵(式(7)~(8)),进行矩阵组装,得到侧边子系统中节点1 的运动方程:


3.2 角点子系统的稳定性条件

3.3 稳定性条件的比较
由于整体模型的稳定性受不同局部区域中最严格的稳定性条件控制,根据式(6)、(21) 和(26),可将采用黏弹性人工边界时显式算法的稳定性条件统一改写为:

侧边和角点子系统的稳定性系数γ和γ均为无量纲系数,仅与内部介质的泊松比、波源距与有限单元长度比/有关。不同区域的稳定性系数γ 随和/的变化情况,如图4 所示;当/=1,5,+∞时稳定性系数γ 随泊松比的变化,当泊松比=0.2,0.3,0.4 时稳定性系数γ 随/的变化,如图5~6 所示。
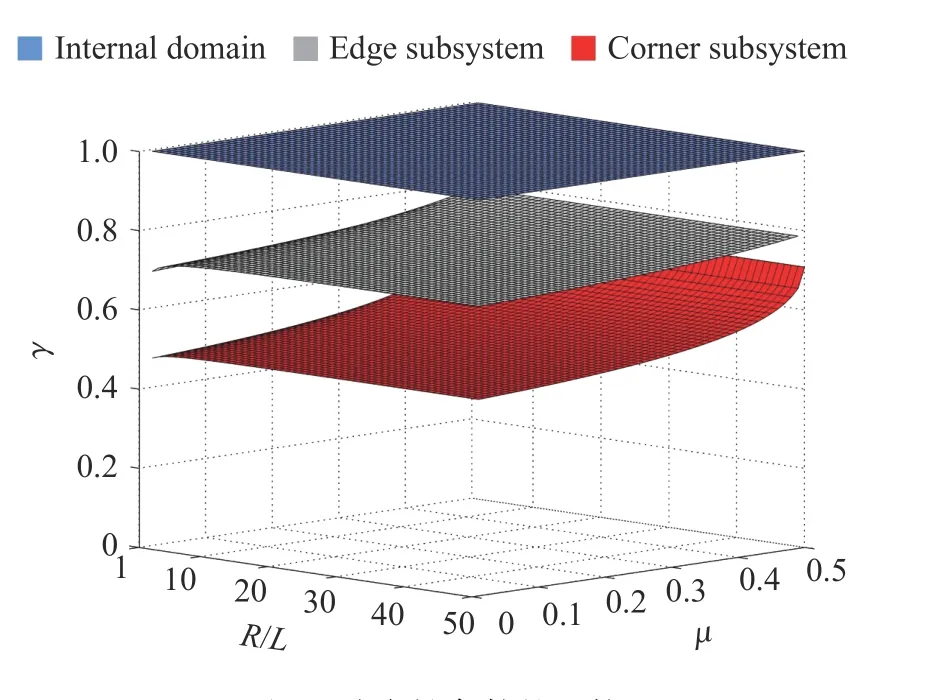
图4 稳定性条件的比较Fig. 4 Comparison of stability conditions
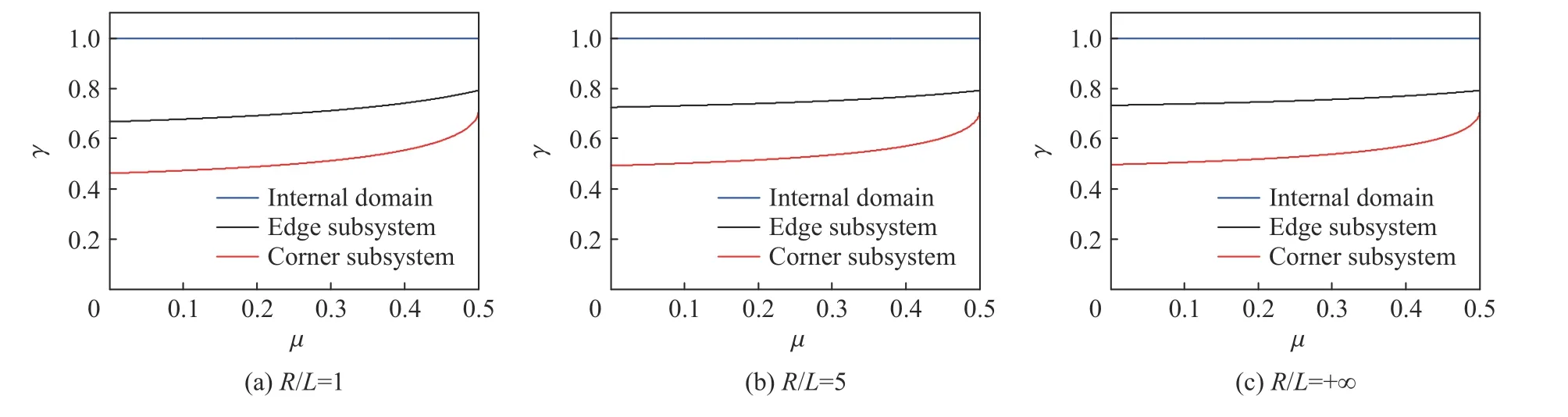
图5 不同R/L 时稳定性系数γ 随泊松比µ的变化Fig. 5 Variations of stability coefficient γ with Poisson’s ratio µ under different R/L

图6 不同泊松比µ时稳定性系数γ 随R/L 的变化Fig. 6 Variations of stability coefficient γ with R/L under different Poisson’s ratio µ
由图4~6 可见,侧边和角点子系统的数值积分稳定性均随泊松比的增大变得宽松,且随着波源距与单元尺寸比/的增大先略为放松,当/>5 时基本保持不变。此外,在不同情况下,角点子系统的稳定性系数均最小,对整体计算模型的稳定性起控制作用,其稳定性条件即为采用黏弹性人工边界时显式时域逐步积分算法的统一稳定性条件。可表示为:

在采用黏弹性人工边界和中心差分法进行动力分析时,根据黏弹性人工边界参数α、α和波源距与单元尺寸之比/及泊松比,即可由式(28)确定稳定的时间积分步长。在实际应用中,为了更方便地确定稳定时间积分步长 Δ,可采纳几种常见情况的稳定性系数,见表2。

表2 建议的几种常见情况的稳定性系数Table 2 Recommended stability coefficients for several common cases
在实际工程中,通常满足材料泊松比 µ≥0.1 、波源距与单元尺寸比/≥5 ,且稳定性条件随泊松比和波源距与单元尺寸比/的增大变得宽松。在实际应用中,为避免复杂的公式计算,可直接采用µ=0.1、/=5对应的稳定性条件作为系统最大稳定积分时间步长的保守估计:

4 稳定性条件验证
4.1 均匀半空间模型
为验证以上稳定性分析的准确性,采用大型通用有限元软件ABAQUS 建立均匀半空间模型,如图7所示。模型尺寸为100 m×50 m,内部介质的密度为2 000 kg/m,剪切波速为200 m/s,泊松比为0.3。采用四节点平面应变单元进行有限元离散,网格尺寸为1 m×1 m。在模型的截断边界处施加黏弹性人工边界,并令人工边界参数α=0.5、α=1.0。在模型中点(点)处施加持时0.2 s、幅值为1 MN 的脉冲荷载,如图8 所示。

图7 均匀半空间模型Fig. 7 The homogeneous half-space model

图8 脉冲荷载Fig. 8 The impulse load
根据以上模型参数,分别采用式(6)、(21)和(26),给出的稳定性条件及式(29)给出的稳定性系数建议值,计算的模型不同区域的最大稳定时间步长见表3。

表3 均匀半空间模型的稳定性系数和最大稳定时间步长Table 3 Stability coefficients and maximum stable time steps of the homogeneous model
分别采用不同的固定时间步长进行显式动力计算,并统计其稳定性状态,结果见表4。提取失稳时计算模型的位移云图,如图9 所示,并比较采用不同固定积分时间步长时模型底部角点(点)的竖向位移,如图10 所示。
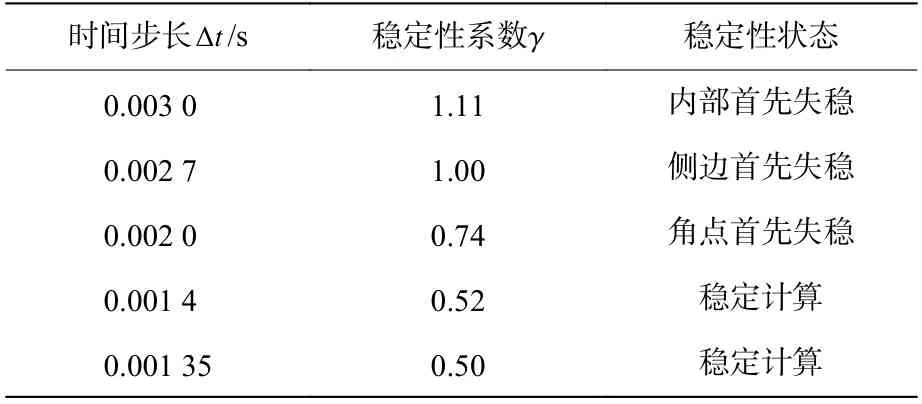
表4 不同固定时间步长时均匀半空间模型的稳定性状态Table 4 The stability states of the homogeneous model under different fixed time steps

图9 均匀半空间模型的位移分布Fig. 9 Displacement distributions of the homogeneous half-space model
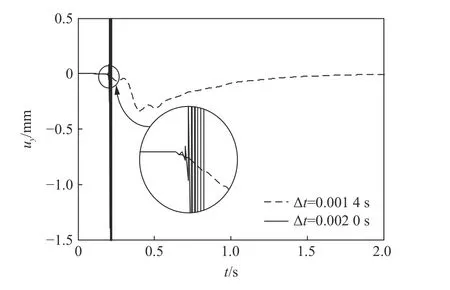
图10 均匀半空间模型底部角点的竖向位移Fig. 10 Vertical displacements of the corner point in the homogenous half-space model
由表3~4 和图9~10,可以得到以下结论:本文中的采用黏弹性人工边界时显式时域逐步积分算法的稳定性条件解析解可准确判断数值计算中的稳定性状态;当所积分时间步长不满足内部计算域、侧边子系统或角点子系统的稳定性条件时,相应区域分别发生失稳,失稳状态如图9 所示;当积分时间步长满足角点子系统的稳定性条件时,可顺利完成整体模型的数值计算,即采用黏弹性人工边界时显式时域逐步积分算法的稳定性条件由角点区控制;由于稳定性系数的建议值比理论值更保守,采用本文中的稳定性系数建议值确定的积分时间步长可保证显式动力计算的顺利完成。
4.2 成层半空间模型
为进一步验证以上结论在复杂场地中的适用性,建立成层半空间模型。如图11 所示,模型尺寸为100 m×100 m,分为上下两层,层厚均为50 m,上层介质的密度、剪切波速和泊松比分别为1 800 kg/m、150 m/s 和0.28,下层介质的密度、剪切波速和泊松比分别为2 200 kg/m、250 m/s 和0.35。采用四节点平面应变单元对计算模型进行有限元离散,网格尺寸为1 m×1 m。在模型截断边界处施加黏弹性人工边界,在模型中点(点)处施加脉冲荷载(见图8)。

图11 成层半空间模型Fig. 11 The layered half-space model
由以上参数计算得到的成层半空间模型不同区域的稳定性系数和最大稳定时间步长见表5,上层介质及其侧边子系统的稳定性条件比下层介质的稳定性条件更宽松,可以判断该模型的数值积分稳定性应由下层介质控制。分别采用不同的固定时间步长进行显式动力计算,并统计其稳定性状态,结果见表6。提取失稳时计算模型的位移云图,如图12 所示,并比较采用不同固定时间步长时模型底部角点(点)的竖向位移,如图13 所示。

图12 成层半空间模型的位移分布Fig. 12 Displacement distributions of the layered half-space model
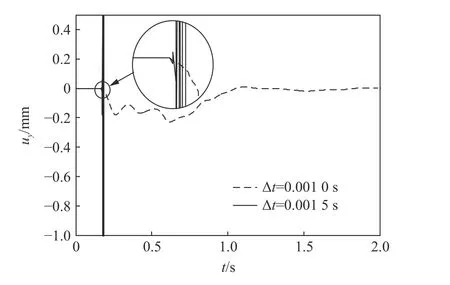
图13 成层半空间模型底部角点的竖向位移Fig. 13 Vertical displacements of the corner point in the layered half-space model

表5 成层半空间模型的稳定性系数与最大稳定时间步长Table 5 Stability coefficients and maximum stable time steps of the layered model
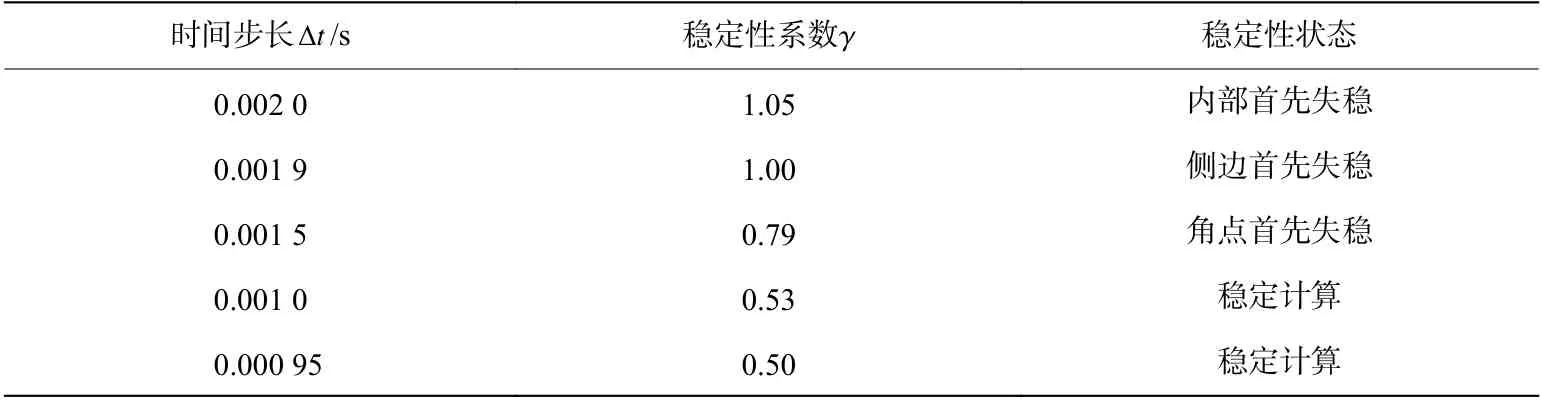
表6 采用不同固定时间步长时成层半空间模型的稳定性状态Table 6 The stability state of the layered model under different fixed time steps
由表5~6 和图12~13,可以得到与第4.1 节相似的结论:本文中稳定性条件解析解可准确判断采用不同积分时间步长进行显式动力计算时整体模型的稳定性状态;整体模型中同一层介质的稳定性由角点区域控制,在实际工程应用中,令积分时间步长满足式(28)的稳定性条件,或将积分时间步长取为由式(29)给出的稳定性系数建议值与内部计算域临界时间步长的乘积,即可顺利完成整体模型的显式动力计算。
5 结 论
以二维黏弹性人工边界为研究对象,利用基于局部子系统的稳定性分析方法研究其在显式时域逐步积分算法中的稳定性,并通过数值算例对稳定性分析的准确性加以验证。具体结论如下。
(1)给出了采用黏弹性人工边界时,模型侧边和角点区域在显式时域逐步积分算法中的稳定性条件解析解,获得了含黏弹性人工边界的整体模型在显示动力计算中的统一稳定性判别准则,在数值模拟时可利用该解析解对整体模型的稳定性进行预判。
(2)考虑黏弹性人工边界影响时,整体模型的数值积分稳定性条件比内部计算域更严格,整体模型的稳定性由角点区域控制。侧边和角点区域的稳定性条件仅与波源距与单元尺寸比/、泊松比和内部计算域的稳定时间步长/有关。随着/和的增大,人工边界区的稳定性变得宽松,当/>5 时,稳定性条件基本保持不变。
(3)分析稳定性条件的控制因素及其影响规律的,给出了采用黏弹性人工边界时显式时域逐步积分算法稳定性系数的保守建议值。在实际应用中,可直接采用该稳定性系数建议值与内部计算域临界时间步长的乘积,作为显式动力计算最大稳定时间步长的估计。
