基于Ring All-Reduce的高扩展性分布式机器学习架构
2022-04-09黄纯悦杨宇翔
黄纯悦 杨宇翔






摘要:如今,机器学习广泛应用于各个行业,然而随着当下各种应用场景的数据量的增大,分布式机器学习几乎成为唯一的选择。因此,各个设备之间的数据通讯的优化十分重要。在参数服务器架构中,参数同步通信量大,参数服务器节点的带宽会成为瓶颈;而在基于Ring All-Reduce的框架下,通信时间受限于环上最慢的连接,当环中GPU节点数变多的时候,会导致延迟变大。该文提出一种基于Ring All-Reduce的分层架构,将计算节点按算力大小分成多个小组,组内使用Ring All-Reduce算法进行同步并行,小组间使用参数服务器架构实现异步并行,保证模型收敛的条件下,兼顾各个节点的负载均衡。
关键词:分布式机器学习;联邦学习;分层Ring All-Reduce
中图分类号:TP18 文献标识码:A
文章编号:1009-3044(2022)06-0054-03
开放科学(资源服务)标识码(OSID):
1 概述
机器学习是当下的热门学科,神经网络作为机器学习的核心技术[1],广泛应用于如自动驾驶、语音识别[2]、文本理解[3-4]、图像分类[5-6]等领域。然而在许多互联网应用场景下,经常会涉及量级很大的计算数据,想要利用单个设备完成机器学习模型的训练是非常困难的,因此分布式机器学习[7]是十分必要的。所以,对设备之间数据通讯的优化具有十分重要的意义。
参数服务器架构[8-9]是最开始被提出来的同步参数的框架,但该架构会受到网络带宽的限制,扩展性较差。
Ring All-Reduce[10-12]架构有效减少了通讯延时和时间开销,但是在环状结构中随着环上节点数目增大,各个设备算力的差异会产生大量的等待时间,从而大大增加时间开销。各种基于Ring All-Reduce架构诸如Hierarchical All-reduce[13]等改进架构,采用了分层的思想,减少了一个组内计算节点的数目,以减少延迟,但组间仍然采用Ring All-Reduce的思想,没有改变同步更新的特性,当有故障节点或算力很低的节点时,仍然会拖慢整体的计算速度。
因此,在本文中会提出一种新的框架:PS-enhanced Hierarchical Ring-based All-Reduce(PS-HRA),将上述两种架构结合,用以进一步减少通信时间开销。同时我们也会分析新算法的时间开销并且与前述算法相比较,以证明该算法的优越性。
接下来论文的框架是:第二部分总结了我们研究的相关工作,介绍了几种传统架构:PS架构、Ring All-reduce架构、Hierarchical All-Reduce架构;第三部分介绍了算法PS-HRA的设计;第四部分计算了PS-HRA算法的时间代价并与传统架构进行了性能比较;第五部分总结了全文并阐述了未来的工作。
2 相關工作
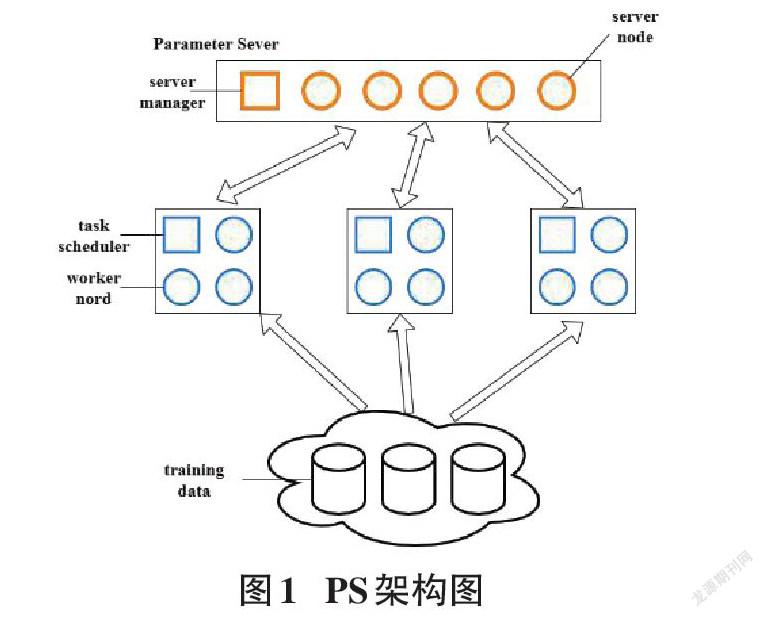
2.1 Parameter Sever架构
Parameter Server(PS)架构是一种分布式机器学习中心化的同步参数的架构,由服务器端和客户端组成。服务器端用来接收客户端的梯度,进行梯度平均。客户端用来向服务器端传送梯度以及利用从服务器端接收到的最新梯度以更新模型。其整体架构如图1所示。
PS架构工作过程如下:每个客户端用自己的局部数据训练得到梯度后,将梯度传送给参数服务器端。参数服务器端接收各个客户端的梯度后,进行梯度平均,再传送给各个客户端。
设有[N]个计算节点,[C]为server计算每字节数据的耗时,[S]为数据块大小,[B]为带宽, [a]为两个通信点间的延时。
则时间开销为:
[2*a+NSB+N*S*C]
此种架构的局限性在于参数同步通信量大,由于会受到网络带宽的限制,扩展性差。
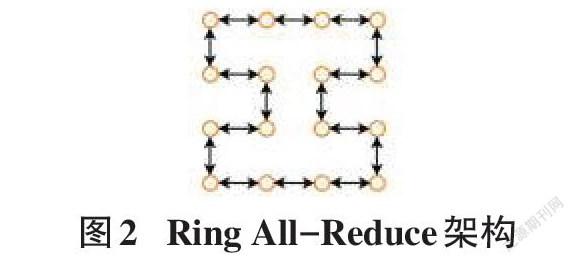
2.2 Ring All-Reduce
Ring All-Reduce算法中,所有的GPU节点只会与其相邻节点进行数据通信。该算法总共有两步: scatter-reduce和all-gather。在第一步中,每个GPU节点依次计算特定的数据块得到梯度并和上一个GPU发送的梯度进行累加,之后发送给下一个GPU节点,假设有[N]个节点,共进行[N-1]次。在这一步结束后,每个GPU节点都会包含一个最终梯度块;在第二步中,相邻节点间进行梯度块的交换,使得每个节点都有最终结果的全部梯度。其架构如图2所示。
假设有[N]个节点,[S]为数据块大小,[B]为带宽,[a]为两个通信点间的延时,[C]为每字节数据的计算耗时。
则时间开销为:
[2*(N-1)*[a+SNB] + (N-1)*[(SN)*C]]
环上的最慢连接会大大增加该算法的通信时间,另外当GPU数量不断增加,延迟也会不断增大。
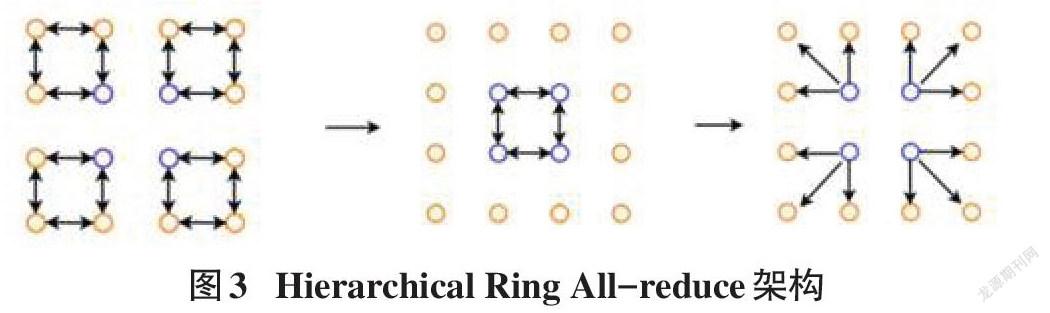
2.3 Hierarchical All-Reduce
Hierarchical All-Reduce是基于Ring All-Reduce进行优化的一种算法,该算法的过程如图3所示。
Hierarchical All-Reduce算法按三步进行:第1步,Intragroup All-Reduce,将所有节点分为[k]组,每组内部进行Ring All-Reduce;第2步,Intergroup All-Reduce,在每个组中选择一个节点,这些节点进行Ring All-Reduce。在第三个阶段Intragroup Broadcast,将更新后的参数传递到所有节点。
假设有[N]个节点,被分为[k]组,设[S]为数据块大小, [B]为带宽,[a]为两个通信点间的延时。
则需要的总时间为:
[2*Nk-1*a+kSNB+2*k-1*a+SkB+Nk-1*kSN*C+k-1*Sk*C+a+SB]
Hierarchical All-Reduce模型采用了分组策略,一定程度上改善了Ring All-Reduce节点数增加导致通信时延过大的局限性,并且通信时间依然受到环上最慢连接的限制。
3 PS-HRA:PS-enhanced Hierarchical Ring-based All-Reduce
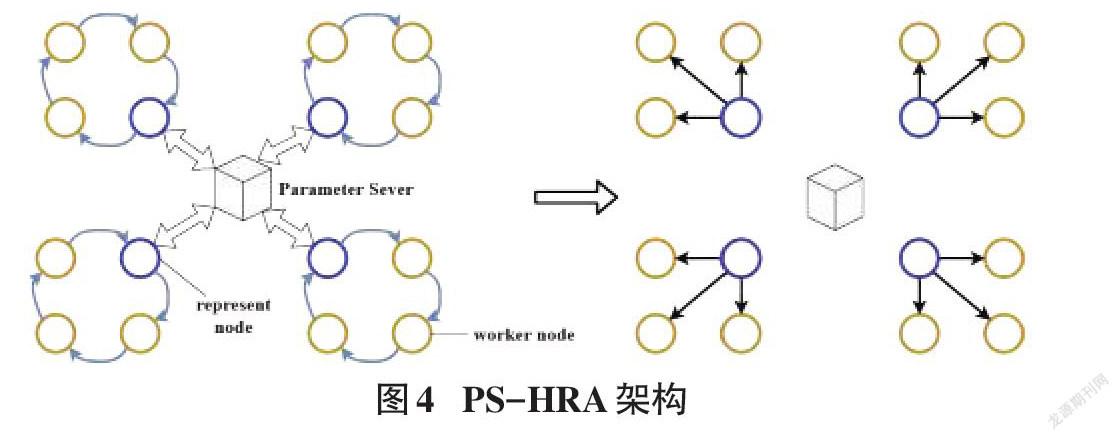
3.1 PS-HRA模型架构
PS-HRA算法综合了去中心化的Ring All-Reduce算法和中心化的PS框架,形成了一个分层的通讯优化框架。它由若干个去中心的节点的环和一个中心节点组成。总的来说,相比于传统的参数服务器架构,中心节点在我们的框架下控制的是各个环而不是单个节点,因此采用我们的通讯框架可以有效地解决中心节点带宽限制的问题,即在仅有一个中心节点的情况下,我们的框架可以扩展更多的计算节点,并保证不会因为带宽问题使传输数据速率限制下降。同时环间采用异步PS架构,在环内计算节点算力相近的条件下,可以改善环间算力差异带来的同步等待问题。
3.2 分组策略
在PS-HRA架构中,中心节点的作用主要有两个,一是作为参数服务器,另一个是工作节点调度器。初启阶段,中心节点根据算力大小将工作节点分组。具体步骤是在中心节点设置一个队列,初启时,各个计算节点训练部分测试样本,当训练完毕时,向中心节点发送完成标识,进入队列。假设有[N]个节点,被分为[k]组当队列中计算节点大于等于[N/k]时,将前[N/k]个计算节点出队列并形成一组进行Ring All-Reduce训练。在环内每个节点可以利用自己的数据集训练出模型的一部分参数,然后在all-gather这一步中相邻节点通过交换参数,使得每个节点获得最终的全部参数。
算法1. PS-HRA分组算法
输入:节点[id] , 節点数目[N], 分组数目[k]
输出:环[ring]
1. [q=initqueue();] //初始化队列
2. [worknode]←[testspeeddemo]; //测试数据发送到工作节点
3. [loop:]
4. [ifworknode[id].status= =OK q.enqueueid; ]//将完成计算的节点加入队列
5. [ifq.size≥N/k {ring←q1…N/k;}] //前[N/k]的计算节点形成环
3.3 环间异步PS架构
Hierarchical All-Reduce算法在环间使用的Ring All-reduce是一个同步算法,没有考虑算力大小差异的问题,无法解决同步开销大的问题,通信时间依旧会受到最慢的连接的限制。PS-HRA在各个环之间采用异步PS架构,可以任意选取其中一个计算节点代表他所在的环和服务器进行通讯。PS架构使用的是数据并行[14]技术,即每个环获得的数据并不一样,每个环把通过训练本地数据的获得模型参数传给中心节点,中心节点将接收来的参数进行聚合更新从而获得最新参数并传送给各个环。由于设置分组策略使得组内节点算力相近,组间节点算力差异大,如果采用同步的PS架构,虽然可以保证模型收敛,但是同步开销比较大,因此采用异步PS架构。
在异步PS架构中,参数服务器收到了一个环传来的梯度之后,不需要收集全部环的参数再进行更新,而是直接去更新参数,得到新的参数值传给代表节点。再由代表节点在环内进行广播,以进行下一轮的训练。这样不会受到算力最慢的工作节点的限制,提高了训练速度,可以很好地解决同步开销的问题。PS-HRA整体流程如下:
1) 执行PS-HRA分组算法,将算力接近的[N]个节点均匀分成[k]个小组。
2) 小组内并行scatter-reduce算法,执行结束之后每个计算节点具有[k/N]个数据块的环内完整参数。
3) 小组内并行all-gather算法,执行结束后每个计算节点具有环内数据块的全部参数。
4) 环内随机选出一个计算节点作为代表节点,向参数服务器发送参数。
5) 参数服务器接收参数直接对参数聚合更新,无须等待其他环。
6) 代表节点接收参数。
7) 代表节点在环内进行参数广播。
8) 各节点更新模型,进行下一轮的训练。
对于传统的参数服务器架构,假设有16个计算节点,中心节点最多可能面临着16个计算节点同时和它进行通讯;假设有4个环,而PS-HRA的通讯模型最多只需要四个计算节点和中心节点通讯,这大大减少了带宽瓶颈。
4 PS-HRA时间代价估计与性能分析
4.1 时间代价估计
假设有[N]个节点,被分为[k]组,设[S]为总的数据量,[C]为每字节数据的计算耗时,[B]为带宽,[a]为两个通信点间的延时。
组内scatter-reduce所需时间为 [Nk-1*a+kSNB+kSN*C]
组内all-gather 所需时间为 [Nk-1*a+kSNB]
组间使用异步PS架构所需时间为 [2*a+SB+S*C]
每组代表节点将更新后的参数传给组内其余节点所需时间为:
[a+SB]
通过计算可得,需要的总时间为:
[2*Nk-1*a+kSNB+Nk-1*kSN*C+3*a+SB+S*C]
4.2 性能分析
为了证明PS-HRA算法性能的优越性,需要在传输时间延迟或节点数量变化的情况下,对比前述四种算法的通信时间。
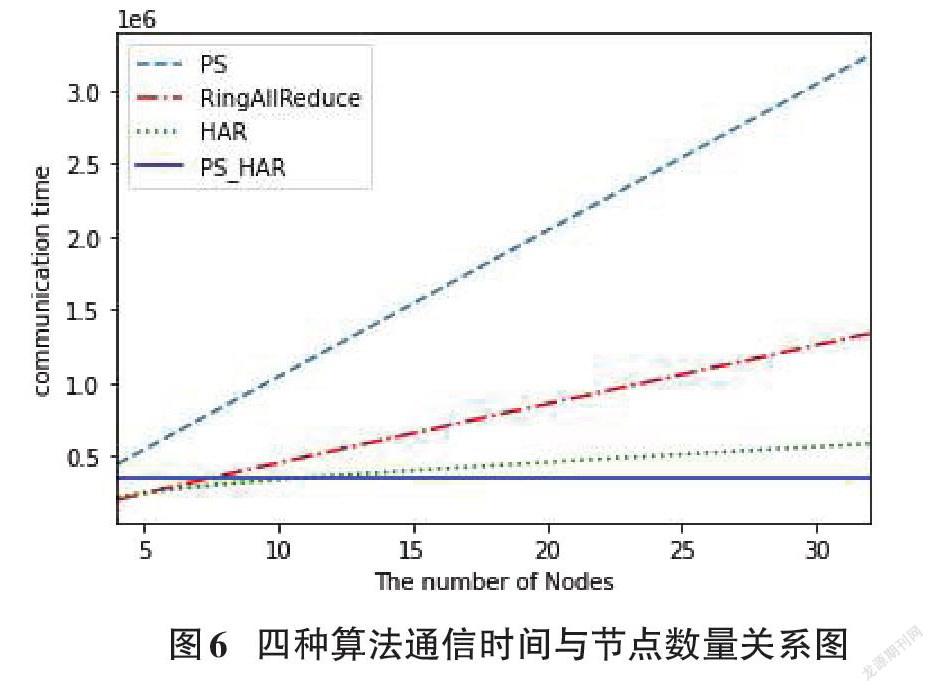
我们模拟了两种情形下前述四种算法的通信时间并绘制了折线图用以比较,如图5、图6所示。
传输延迟包括算力差的节点带来的同步开销,所以由图5可知,传输延迟越大,Ring All-Reduce的通信时间越长;然而PS架构的通信时间变化很小,其性能受传输延迟影响小。另外,不难发现PS-HRA的通信时间最少且随着传输延迟的增大,其性能的优越性更加显著。
由图6可知,随着节点数的增加,PS-HRA算法的通信时间基本不变,而其余三种算法的通信时间会随着节点数的增加而不断变大。当节点数较大时,PS-HRA的通信时间最少。
5 结束语
PS架构会受到带宽的限制,而Ring All-Reduce通信时间受限于环上最慢的连接并且通信延迟会随着环中节点数增加变大。在本文中我们将上述两种算法相结合,进一步优化了算法的性能。在这篇文章中,首先我们介绍了相关工作和新算法PS-HRA的设计。然后,我们分析了PS-HRA算法的性能和时间开销,并且比较证明了我们算法性能的优越性。
在未来的研究中,我们会在更多、更复杂的情况下进一步验证我们通信策略的有效性。另外,我们会把我们的通讯策略应用到更多机器学习的场景中。
参考文献:
[1] 杜海舟,黄晟.分布式机器学习中的通信机制研究综述[J].上海电力大学学报,2021,37(5):496-500,511.
[2] Deng L,Li J Y,Huang J T,et al.Recent advances in deep learning for speech research at Microsoft//2013 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2013: 8604-8608.
[3] Turian J,Ratinov L,Bengio Y.Word representations:a simple and general method for semi-supervised learning[C]//ACL '10:Proceedings of the 48th Annual Meeting of the Association for Computational Linguistics.2010:384-394.
[4] Liang X D,Hu Z T,Zhang H,et al.Recurrent topic-transition GAN for visual paragraph generation[C]//2017 IEEE International Conference on Computer Vision.Venice,Italy:IEEE,2017:3382-3391.
[5] Yan Z C,Piramuthu R,Jagadeesh V,et al.Hierarchical deep convolutional neural network for image classification:US10387773[P].2019-08-20.
[6] Yan Z C,Zhang H,Wang B Y,et al. Automatic photo adjustment using deep neural networks[J].ACM Transactions on Graphics (TOG), 2016, 35(2):1-15.
[7] Chen T, Li M, Li Y, et al.Mxnet:A flexible and efficient machine learning library for heterogeneous distributed systems[J].arXiv preprint arXiv:1512.01274, 2015.
[8] Li M, Zhou L, Yang Z, et al. Parameter server for distributed machine learning[C]//Big Learning NIPS Workshop,2013, 6: 2.
[9] Li M,Andersen D G,Park J W,et al.Scaling distributed machine learning with the parameter server[C]//11th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 14). 2014: 583-598.
[10] Tokui S,Okuta R,Akiba T,et al.Chainer: A deep learning framework for accelerating the research cycle[C]//Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.2019:2002-2011.
[11] Tokui S,Oono K,Hido S,et al.Chainer: a next-generation open source framework for deep learning[C]//Proceedings of workshop on machine learning systems (LearningSys) in the twenty-ninth annual conference on neural information processing systems (NIPS).2015, 5:1-6.
[12] Sergeev A,Del Balso M.Horovod: fast and easy distributed deep learning in TensorFlow[J].arXiv preprint arXiv:1802.05799,2018.
[13] Jiang Y,Gu H,Lu Y,et al.2D-HRA:Two-Dimensional Hierarchical Ring-Based All-Reduce Algorithm in Large-Scale Distributed Machine Learning[J]. IEEE Access,2020,8:183488-183494.
[14] 李曉明.数据并行计算:概念、模型与系统[J].计算机科学,2000,27(6):1-5.
【通联编辑:谢媛媛】
