斯通利波在渗透地层和裂缝带的反射及透射:解析和数值方法模拟对比

夏飞月， 苏远大,3， 唐晓明,3*

1 中国石油大学(华东)地球科学与技术学院， 山东青岛 266580 2 中国石油大学(华东)深层油气重点实验室， 山东青岛 266580 3 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室， 山东青岛 266071

0 引言

探测地下渗透结构的渗透性及分布位置在油气勘探开发中具有重要意义，水力压裂缝带渗透性的评估一直是这方面的一项重要研究课题.人们通常利用VSP(Vertical Seismic Profile，垂直地震剖面)(Minato et al., 2017)和声波测井(Tang and Cheng, 1993)中的斯通利波进行裂缝带和渗透地层的识别和评价.斯通利波是沿着井壁传播的导波，在井径不规则处(Tezuka et al., 1997)、地层弹性性质或渗透性能改变处均会发生反射及透射.Tang和Cheng(1993)将简化的Biot-Rosenbaum(BR)理论(Tang et al., 1991a)与井筒波导的一维传播理论结合得到的等效波数法应用于渗透地层的斯通利波反射及透射问题.一维等效波数法的中心思想和巧妙之处在于：无论裂缝带的情况有多么复杂，只要确定声波在裂缝地层传播的等效波数，就可以有效地模拟裂缝地层对波传播的影响(即波的反射和透射).这一思想在Kostek等(1998a,b)对单个和多个平板裂缝模型的模拟结果中得到了很好的验证.简化的BR理论能够快速高效地模拟低频井孔斯通利波对渗透地层的响应，在地层(Tang and Cheng, 1996; 庄春喜等, 2019)和裂缝渗透率反演(Tang et al., 1991b)有较好应用.然而，基于该理论的一维等效波数法主要考虑了地层孔隙流体流动而对骨架的影响考虑不足(唐晓明和郑传汉, 2004)，再加上斯通利波一维路径传播的近似处理，该方法的有效性需要进行评估.裂缝地层对测井声波影响复杂，研究和分析裂缝带的测井声波响应对于测井数据解释有重要意义(阎守国等, 2015).对于较为复杂的径向和轴向都有变化的渗透结构，如低渗透地层中径向有限长延伸的裂缝带(Hornby et al., 1992)，一维等效波数法难以进行模拟计算.

由于所涉问题和方法的重要性，有学者利用实验(Zhu et al., 1992)和现场数据(Tang et al., 2011)对一维等效波数法进行过验证，但基于基础理论和严格数值模拟的对比和验证工作还不多见.Bakulin等(2005)和Alexandrov等(2007)利用一维等效波数法与基于孔弹理论的有限差分法来研究斯通利波在裸眼井和套管井渗透地层模型的反射及透射，两种方法计算的斯通利波反射系数在0～1 kHz吻合较好.本文的目的是将前人的工作进一步深入，利用孔弹有限差分方法(Guan and Hu, 2011; Ou and Wang, 2019)和一维等效波数法(Tang and Cheng, 1993)研究不同地层厚度、渗透率和孔隙度的渗透地层对斯通利波反射及透射的影响.两种方法计算结果验证了有限差分法模拟结果的正确性和一维等效波数法在0～2 kHz频段(Tang et al., 2011)内的可靠性.不同渗透率、不同结构裂缝带的有限差分数值模拟结果有助于分析和解释斯通利波在高渗透裂缝带的反射及透射现象，为声波探测方法的实际应用和分析方法适用性提供了理论依据.

1 渗透地层测井斯通利波传播的理论和方法

1.1 Biot理论的有限差分近似方法

Biot(1956a，b，1962)对饱含流体孔隙介质建立了弹性波动理论.将井外地层作为饱含流体的孔隙介质，可以用Biot理论来求解渗透地层的声波测井问题.Guan和Hu(2011)给出了频域均匀各向同性孔隙介质弹性波动方程组，

(1)

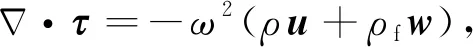
(2)

(3)

(4)

其中w是流体和固体的相对位移，u是固体的位移，τ是应力张量，I是克罗内克张量，p是孔隙流体压力.ω是角频率，ρf和η分别是孔隙流体密度和流体黏度，ρ是地层有效密度，满足ρ=ρs(1-φ)+ρfφ，φ是地层孔隙度.C，M和H是孔隙介质参数的组合(Biot, 1962)，

(5)

C=(1-Kb/Ks)M,

(6)

H=(1-Kb/Ks)2M+Kb+4G/3,

(7)

其中Ks是固体颗粒的体积模量，Kf是孔隙流体体积模量，Kb和G分别是岩石干燥体积模量和剪切模量.

Johnson等(1987)通过理论分析给出了描述Biot介质孔隙流体流动特征的动态渗透率κ(ω)如下：

(8)

其中ωc=φη/(α∞ρfκ0)为Biot特征频率，κ0为静态达西渗透率.在特征频率以下的频段(ω≪ωc)，κ(ω)→κ0，孔隙流体的运动是静态压力驱动下的扩散型黏滞流动，即达西渗流；在特征频率以上的频段(ω≫ωc)，κ(ω)→iηφ/(α∞ρfω)，流体运动是一种传播型波动.其中α∞是孔隙弯曲率，m=φΛ2/(α∞κ0)是一个无纲量组合,其中的Λ是孔隙体面比.对于裂缝渗透地层，α∞=1，m=12；对于孔隙渗透地层，α∞=3，m=8(Tang et al., 1991a; Tang and Cheng, 1993).

由于动态渗透率中含有根号项，不便于用有限差分法将方程(1)求解.为解决这个问题，Masson等(2006)将κ(ω)用以下形式替换

(9)

将(8)式中的根号取泰勒展开的一阶项便可得到(9)式，该近似满足条件|4ω/(mωc)|<1.一般情况下，式(8)和(9)在由低到高的整个频段内都十分符合(Masson et al., 2006; Guan et al., 2009)，因此可以将(9)式看作是为实现Biot理论有限差分方法所做的一个有效近似.由此可以将频域中的Biot方程组变换到时域的速度-应力形式，整理得到

(10)

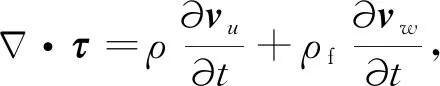
(11)

(12)

(13)

以上方程组的系数是线性的(非时间或频率的函数)，很适合用有限差分方法求解.对于声波测井问题，可以将公式(10)—(13)在柱坐标系表示(Randall et al., 1991; He et al., 2012)，将介质的模型参数在空间域内网格化，并利用交错网格和中心差分格式对以上方程组进行离散化求解，时间和空间的差分均采用二阶近似.前人对以上孔弹方程组的有限差分求解过程进行了详细阐述(Guan and Hu, 2011; Ou and Wang, 2019)，因此本文将不再赘述.模型的吸收边界采用不分裂的完美匹配层(Nonsplitting Perfectly Matched Layer, NPML),具体公式推导可参见Wang和Tang(2003)和Song等(2005)；对于模型中流体、弹性固体和孔隙固体共存的介质，通过设置参数仍然可以用Biot方程组((10)—(13))来表示(Guan and Hu, 2011; 阎守国等, 2015; Ou and Wang, 2019).在流体中，ρ=ρf，φ=1，G=0，C=M=H=Kf，C2=ρf，C1=0，τ=-pI，vw=0,方程(11)和(12)简化为流体中表示的声压波动方程组.在弹性固体中，ρf=ρ=ρs，φ=0，G=Gs，C=Ks，H=Ks+4Gs/3，M=∞，C1=∞，C2=∞，p=0，vw=0，方程(11)和(12)退化为弹性固体中的应力速度表示的波动方程组，其中ρs，Ks和Gs分别表示弹性固体的密度、体积模量和剪切模量.因此，波动方程(10)—(13)可统一描述三种介质的声场，不同介质衔接处可采用物质参数平均技术(Guan and Hu, 2011).

1.2 一维等效波数法

井中斯通利波具有良好的导波性质，在低频范围内井孔声场是相对稳定的.因此，可以利用导波一维传播理论(White, 1983; Hornby et al., 1989; Tang and Cheng, 1993; Tezuka et al., 1997; Bakku et al., 2013)来描述斯通利波的传播特征，这包括了两个重要的假定，一是斯通利波的能量主要集中在井内；二是斯通利波在渗透地层中的传播主要受井孔与地层的流体交换影响，受地层弹性性质影响较小.将一维传播理论用于非均匀波导的反射和透射时，下述的等效波数理论使问题的求解变得十分简便.对于单个渗透夹层，Tang和Cheng(1993)推导得到斯通利波的反射系数R及透射系数T如下：

(14)

(15)

其中L表示夹层厚度，k1表示夹层上下无限大地层的波数，k2表示中间夹层的波数，a1和a2是井孔截面积.对于多个夹层的情况，可以利用一维传播矩阵计算(Tezuka et al., 1997),每一夹层中的波传播由该层的波数控制.对于弹性地层，采用无限大地层斯通利波波数(White, 1983)；对于渗透地层，采用简化BR理论推导的斯通利波波数(Tang et al., 1991a)，

(16)

R是井孔半径，a是仪器半径(本文未考虑仪器的情况，所以取a=0)，ke是无限大弹性地层的斯通利波波数(White，1983)，K1和K0分别是一阶和零阶变型贝塞尔函数，D是孔隙流体的扩散率(唐晓明和郑传汉, 2004).

将一维等效波数的解析方法和有限差分法数值方法用来研究斯通利波在渗透地层的反射及透射有以下意义：等效波数法有明确的物理意义和简洁的数学描述，可以快捷地得到模拟结果，但该方法主要模拟地层渗透性的影响而对地层弹性的影响考虑不足(唐晓明和郑传汉, 2004)，再加上所做的简化和近似，其结果的精度和有效性需要评估.孔弹有限差分方法对地层的弹性和渗透性的影响均包括在内，可对分层界面处波在井内外的能量分布和传递进行模拟，但相对于前一方法而言计算费工耗时.通过两种方法计算结果的比较，可以加深对斯通利波在渗透层的反射和透射问题的物理机制的理解并相互验证两种方法的结果，计算结果对照的差异可以区分地层弹性性质和渗透率的影响.对于等效波数法，在验证其有效性和适用范围后，可以利用该方法的快速计算优点来反演模型参数(Tang et al., 1991b)；而孔弹有限差分方法更有用的功能是做复杂的模型计算，如对于前一方法不能模拟的轴向和径向分层变化的复杂情况.

1.3 有限差分法对均匀渗透地层的验证

数值算法的准确性是衡量时域有限差分方法(Finite-Difference Time-Domain method,FDTD)的重要标准，对于裸眼井均匀渗透地层模型，可用实轴积分法(Real-Axis Integral,RAI)(Schmitt,1988; Chen et al., 2014)计算结果对数值方法进行验证.表1给出不同地层的流体和弹性参数，渗透地层的干燥体积模量和剪切模量可以用纵横波速度计算(Norris, 1989; Tang et al., 1991a).为了验证有限差分在中高渗透率范围的可行性，计算的裸眼井地层模型分别为孔隙渗透地层和裂缝渗透地层.对于孔隙渗透地层，孔隙度及渗透率分别为φ=0.25和κ0≈10-12m2，一般砂岩地层孔隙曲率α∞=3，无量纲常数m=8，由此可得κ(ω)中的Biot特征频率ωc=50 kHz.对于裂缝渗透地层，裂缝孔隙度和渗透率与地层所含裂缝开度总和相关(Tang and Cheng, 1993)，定义式如下所示：

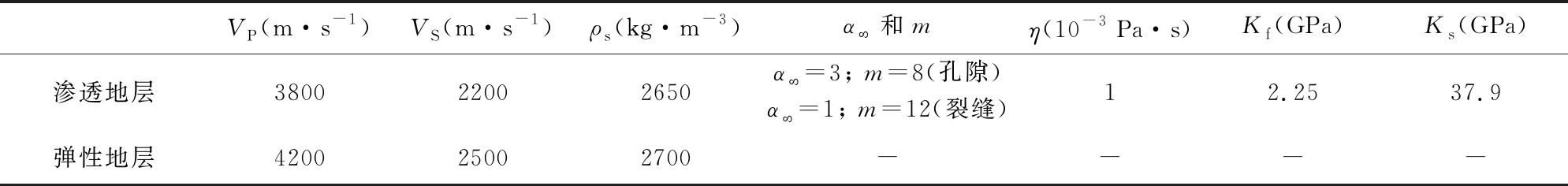
表1 弹性和渗透地层参数表

(17)

该式表示厚度为L的地层含有n条开度为L0的裂缝，一般情况下裂缝开度范围为0.001 mm到1 mm(Hornby et al., 1992).裂缝渗透地层孔隙曲率α∞=1，表示流体在直的裂缝通道内流动；由条件Λ=L0得到无量纲常数m=12.Tang等(1991a)理论证明通过以上参数设置，裂缝导通率(Tang and Cheng, 1989)可以用动态达西渗透率(式(8))来表示，因此该参数下孔隙渗透介质可以表征多条裂缝的斯通利波响应(Tang and Cheng, 1993; Kostek et al., 1998b; Minato et al., 2017).对于人工压裂区的高渗透裂缝带，取平均裂缝宽度L0=0.049 mm，裂缝孔隙度φ=0.25，计算得到平均渗透率κ0≈5×10-11m2，此时Biot特征频率ωc=5 kHz.

(18)

f0是声源主频，Tc代表声源脉冲宽度.为激发井孔中的低频斯通利波，取声源主频f0=1 kHz，声源脉宽Tc=2 ms.

图1a和1b分别是孔隙和裂缝渗透地层阵列声压波形图，红色虚线为有限差分(FDTD)解，黑色实线为实轴积分(RAI)解，两种方法计算的阵列波形以第一道波幅最大值做归一化.声源到第一个接收器的距离为0.5 m，接收器间距为0.5 m(图1a)和0.2 m(图1b)，裂缝渗透地层具有较高的渗透率，波幅衰减很大，因此缩短接收间距以显示波形特征.对于孔隙和裂缝渗透地层模型，有限差分数值解和解析解计算的波形相位和幅度符合十分好.尽管为实现有限差分解做了式(8)的近似，中、高渗透率地层的斯通利波传播模拟仍具有较高的计算精度.因此，有限差分方法提供了较为精确的Biot理论数值解，可以作为验证一维等效波数法的理论参照.

图1 两种方法(红色虚线：有限差分；黑色实线：实轴积分)计算的渗透地层中沿井壁传播的斯通利波阵列声压波形图

2 对复杂渗透地层模型的应用

由于在实际测井数据处理中主要提取0～2 kHz的斯通利波数据进行渗透结构的识别和评价(Tang et al., 2011)，本文主要研究0～2 kHz测井斯通利波在复杂渗透地层的反射及透射.首先利用有限差分方法和一维等效波数法模拟斯通利波在单个和多个渗透夹层的反射及透射，考察等效波数法在各条件下的适用性.对于等效波数法难以模拟的复杂渗透模型，如井孔周围径向和轴向分布的裂缝带，可采用有限差分方法进行模拟.一维等效波数法通过公式(14)和(15)直接给出频域中单个渗透夹层的斯通利波反射和透射系数；有限差分得到的是时域波形，需要用反射、透射和直达(即入射)斯通利波傅里叶变换后的振幅谱来计算这些系数，如(19)式：

(19)

式中的RWV、TWV和DWV分别为反射、透射和直达斯通利波的振幅谱.

2.1 斯通利波在孔隙渗透地层的反射及透射

首先考虑Tang和Cheng(1993)文章中的单个渗透夹层模型：弹性地层中含有1 m厚孔隙渗透地层(表1)，井孔半径为0.13 m.改变孔隙渗透地层的孔隙度和渗透率，由低孔低渗(φ=0.08，κ≈10-15m2)到高孔高渗(φ=0.35，κ≈2×10-12m2)变化.图2为两种方法计算的斯通利波反射及透射系数，有限差分法(实线)和等效波数法(虚线)计算结果在0～2 kHz都十分吻合，但在大于1 kHz的较高频段出现一些差异.这些差异随着孔隙度和渗透率升高逐渐变小，其变化趋势可以在斯通利波透射系数图(图2b)明显看到.当地层孔隙度和渗透率增加，斯通利波反射系数在整个频段内增加，低频(<0.8 kHz)增加较为明显；透射系数在整个频段内降低，高频(2 kHz)降低较为明显.图2所示的低频反射增强和高频透射减少现象反映的是斯通利波在渗透地层的波速降低(主要发生在低频)和波幅衰减(随频率增加)的物理本质，在两种方法的模拟结果中都得到很好的体现.反射系数随频率变化的峰、谷现象是夹层上、下界面反射波相互干涉造成的，稍后有进一步讨论.

考虑图3所示的多个渗透夹层的情况，在无限大弹性地层中，厚度为2.4 m的低孔渗地层(φ1=0.08，κ1≈10-15m2)含有一定厚度的高孔渗夹层(φ2=0.35，κ2≈2×10-12m2)，井孔半径为0.13 m.图4为高孔渗夹层在不同厚度(0.4 m, 0.8 m, 1.0 m)下两种方法计算得到的斯通利波反射及透射系数，有限差分法(实线)和等效波数法(虚线)的结果吻合良好.值得注意的是等效波数法仅考虑井壁上(忽略渗透夹层之间)流体的交换(Tang and Cheng, 1993)，但计算结果仍与考虑了夹层间流体交换的有限差分结果十分一致.随着高孔渗夹层厚度增加，斯通利波透射系数在整个频段内单调降低，反射系数的峰值向低频移动，这是由于高孔渗夹层厚度变化引起的上、下反射波相互干涉造成的.

接下来讨论图3模型中高孔渗夹层的渗透性变化对斯通利波反射及透射的影响，保持高孔渗夹层厚度为1 m不变，改变地层的孔渗参数(φ=0.15和κ≈2×10-13m2,φ=0.25和κ≈10-12m2，φ=0.35和κ≈2×10-12m2)，其他参数与图4所用参数一致.图5是高渗透夹层在3种不同孔渗参数下两种方法计算的斯通利波反射(a)及透射(b)系数，有限差分法(实线)和等效波数法(虚线)的结果吻合较好，但2 kHz附近存在较大差异.随着中间高孔渗夹层的渗透性增强，该差异有所减小，此规律与图2相同.并且与图2单个渗透性夹层对比，图5中高孔渗夹层在相同参数(φ=0.35和κ≈2×10-12m2)下的斯通利波反射及透射系数曲线形态十分相似，说明在低孔渗背景下，斯通利波的反射及透射由高孔渗地层控制.

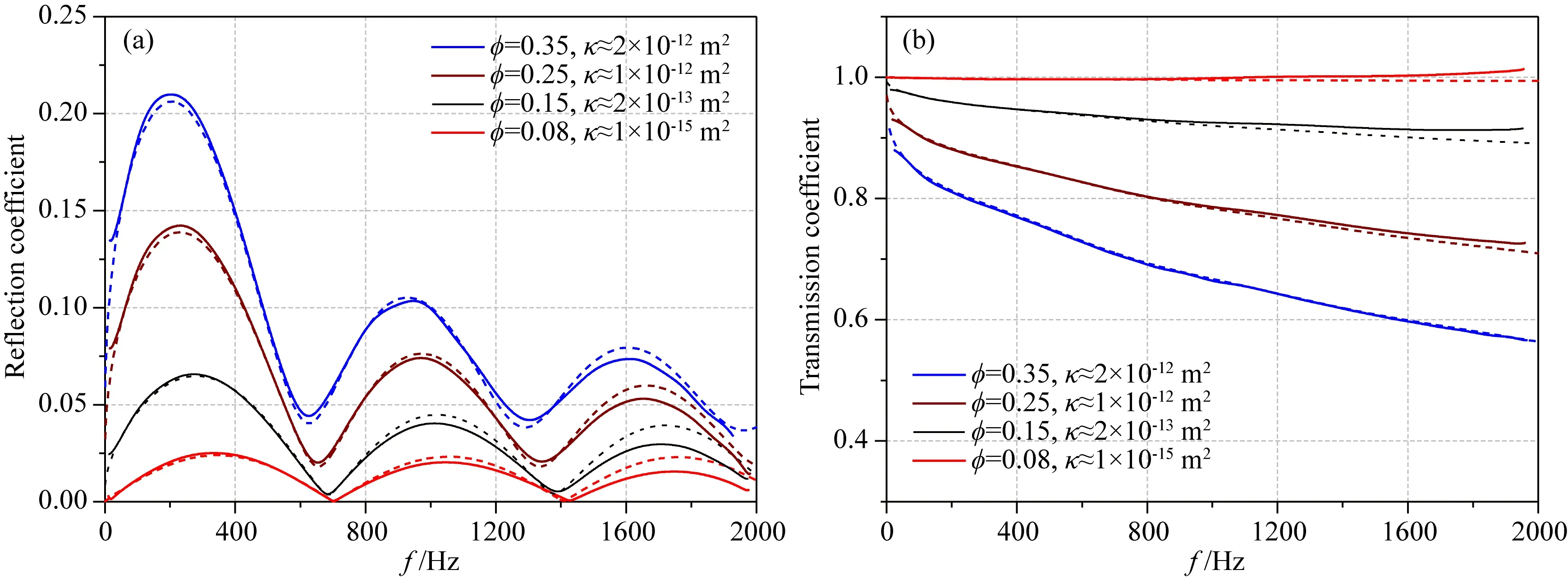
图2 4种孔渗参数下两种方法计算的单个孔隙渗透夹层(Tang and Cheng, 1993)的斯通利波反射(a)及透射(b)系数图实线是有限差分计算结果；虚线是一维等效波数法计算结果.

图3 多个渗透夹层模型.在无限大弹性地层中，2.4 m厚的低孔渗地层(φ1=0.08，κ1≈10-15m2)含有一定厚度的高孔渗(φ2=0.35，κ2≈2×10-12m2)夹层

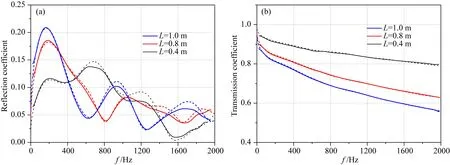
图4 图3模型中高孔渗夹层在3种厚度(0.4 m, 0.8 m, 1.0 m)下的斯通利波反射(a)及透射(b)系数图

图5 图3模型中高孔渗夹层在3种不同孔渗参数下的斯通利波反射(a)及透射(b)系数图

2.2 斯通利波在高渗透裂缝带的反射及透射

斯通利波分析在裂缝及裂缝带的识别和评价有着重要应用(Tang and Cheng, 1993; Tang et al., 2011).天然和人造裂缝往往会在井孔附近形成轴向和径向延伸的裂缝带(Hornby et al., 1992; Medlin and Schmitt, 1994),裂缝带的存在大大增加了井壁附近的渗透性，使得斯通利波在裂缝带产生明显的衰减和较强的反射.对于轴向和径向都有变化的裂缝带，我们用有限差分数值方法来研究斯通利波的传播特征.地层模型如图6所示，位于无限大弹性地层中厚度为2.4 m的低孔渗地层含有径向和轴向有限延伸的裂缝带.弹性地层和低孔渗地层骨架及流体参数与图3一致，裂缝带骨架参数为表1渗透地层参数，裂缝孔隙度φ=0.25，孔隙曲率α∞=1，m=12.

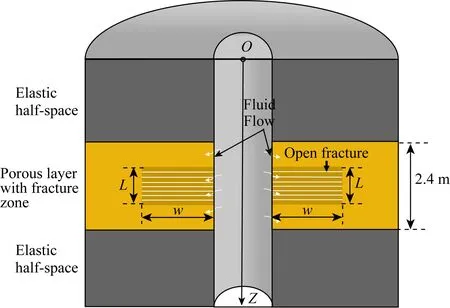
图6 高渗透裂缝带模型.位于无限大弹性地层中厚度为2.4 m的低孔渗地层(φ1=0.08，κ1≈10-15m2)含有轴向延伸长度为L，径向延伸长度为w的高孔渗裂缝带

图7是裂缝带在不同渗透率下有限差分计算的斯通利波反射(a)及透射(b)系数.裂缝带径向延伸长度w=0.2 m，轴向延伸长度L=1 m，渗透率分别取8×10-12m2、2×10-11m2和5×10-11m2，对应的Biot特征频率分别为31.25 kHz、12.5 kHz和5 kHz.当裂缝带渗透率由8×10-12m2变化到2×10-11m2时，斯通利波反射(透射)系数在高频范围(大于0.6 kHz)增加(降低)显著.当渗透率由2×10-11m2变化到5×10-11m2时，斯通利波反射系数在整个频段处于高值且0～1 kHz和1～2 kHz的差异变小，波峰与波谷较为清晰；透射系数曲线变化较为复杂，在低频段降低后随频率增加稍有升高.由于高渗透率条件下裂缝带流体渗流接近Biot特征频率，由黏滞流动向传播波动过渡(Johnson et al., 1987)，因此波的透射系数随频率的变化并不是单调降低.

图7 图6模型中裂缝带在不同渗透率(8×10-12m2，2×10-11m2，5×10-11m2)下的斯通利波的反射(a)及透射(b)系数图

考察裂缝带径向延伸长度的影响.保持图6模型参数不变，裂缝带渗透率κ≈2×10-11m2和轴向延伸长度L=1 m，计算裂缝带径向延伸长度w在不同取值(0.05 m, 0.1 m, 0.3 m, 0.5 m, 无限长)下的斯通利波响应.图8为裂缝带的斯通利波反射及透射系数计算结果.当0.05 m≤w≤0.3 m时，斯通利波反射系数先在整个频段内明显升高，0.1 m≤w≤0.3 m时仅在低频(<1 kHz)升高较为明显，透射系数在整个频段内大幅降低.当w>0.3 m时，斯通利波反射系数在低频较小幅度上升，透射系数在低频降低高频稍有升高，最后反射和透射系数趋近于无限长延伸裂缝带的曲线.模拟结果表明斯通利波激发的孔隙流体渗流的穿透深度有限，是一种与频率有关的趋肤效应(Zhao et al., 1993)，裂缝带径向长度在0.1 m内增加时，斯通利波反射系数在0～2 kHz频段内均升高，反射系数仅低频部分(<1 kHz)对径向长度大于0.1 m的裂缝带有响应；斯通利波透射系数则在全频段(0～2 kHz)对0.3 m内径向长度变化的裂缝带响应灵敏.

最后，考察图6模型中裂缝带轴向延伸长度变化对斯通利波的影响.固定裂缝带径向长度w=0.2 m，其他参数与图8一致，计算轴向长度L不同取值(0.4 m, 0.8 m, 1.0 m, 1.5 m)下斯通利波响应，结果如图9所示.裂缝带轴向变化引起的斯通利波反射及透射系数变化规律与渗透地层类似(图4)；斯通利波反射系数峰/谷值及其变化与裂缝带L值变化引起的上、下层界面反射波干涉有关；透射系数随L增加在整个频段单调降低.这是因为无论裂缝带的径向长度如何，其产生的波幅衰减随波在衰减带的传播距离增加而增加.

图8 图6模型中裂缝带在不同径向延伸长度(0.05 m，0.1 m，0.3 m，0.5 m，无限长)下的斯通利波的反射(a)及透射(b)系数图

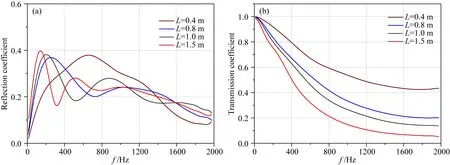
图9 图6模型中裂缝带在不同轴向延伸长度(0.4 m，0.8 m，1.0 m，1.5 m)下的斯通利波的反射(a)及透射(b)系数图

3 结论

本文利用Biot理论研究了测井斯通利波通过渗透性地层时的传播特征.通过有限差分和一维等效波数法对渗透地层的数值模拟结果对比，分析和验证了一维等效波数法在渗透地层模拟的有效性.对于等效波数法难以模拟的复杂裂缝带模型，有限差分方法给出了不同渗透率、轴向和径向延伸长度下裂缝带的斯通利波响应.主要结论如下：

(1) Biot理论的有限差分数值方法对渗透地层的测井斯通利波模拟具有较高精度；通过与一维等效波数法的计算结果对比，验证了后者在0～2 kHz范围内模拟结果的可靠性，为等效波数法的实际应用提供理论依据.

(2) 斯通利波的反射及透射由高渗透地层和裂缝带控制.波在渗透地层的波速降低(主要发生在低频)和波幅衰减(随频率增加)使得斯通利波反射系数在低频段升高，透射系数随频率单调降低.斯通利波反射系数峰/谷值随地层上、下层界面距离增加向低频移动，透射系数则在整个频段内降低.

(3) 斯通利波在渗透地层激发的流体渗流是一种穿透深度有限的趋肤效应，要达到0.1 m以上的探测深度，需要使用较低的激发频率(0～2 kHz)，此频段内的斯通利波反射和透射系数对井壁附近裂缝带的渗透性能均有响应.随着渗透率升高，Biot特征频率降低，流体渗流具有波动特征，斯通利波反射系数，特别是透射系数呈较复杂变化趋势.

本文的方法和结果为利用测井斯通利波数据分析和识别裂缝型渗透地层以及反演渗透性能提供了理论基础，有助于水力压裂的高渗透地层和裂缝带的识别和评价.