考虑撬棒的双馈型风场集电线速断保护

2022-04-08李旭辉谢百煌黄晓勇徐岩

电气传动 2022年7期

李旭辉，谢百煌，黄晓勇，徐岩

（1.国网陕西省电力公司商洛供电公司，陕西商洛 726000；2.国网陕西省电力公司调控中心，陕西西安 710048；3.华北电力大学电力工程系，河北保定 071003）

作为目前技术最为成熟、经济效益最高的可再生能源[1-2]，风电系统的应用得到了能源可持续发展研究领域的广泛关注。在已经建成的风电场中，双馈风机（doubly-fed induction generator，DFIG）由于具有变速调频，控制灵活，换流器体积小、成本低等优点，成为了当前主流的机型[3]。不同于传统的同步发电机及异步电动机，双馈风机定子侧直接连接与电网、转子侧通过电压源型换流器（voltage source converter，VSC）连接与电网的独特方式，使得其需要依靠撬棒（Crowbar）电路来完成交流电网故障时的低电压穿越[4-5]。撬棒电路中卸流电阻的投入将使故障状态下的DFIG具有弱馈性[6-7]，从而影响保护系统的测量值，造成传统过流保护方案的误判，降低风电场内部的可靠性与并网系统的稳定性[8]。因此，研究撬棒动作后DFIG详细的故障电流及阻抗特性对实现风电场及其并网系统的安全有效运行具有重要意义[9-17]。

文献[9-10]分析了撬棒动作后DFIG三相短路的电流计算方法，并根据对故障电流的估计，提出了撬棒电路中卸流电阻的选取原则；文献[11]通过深入分析DFIG控制系统在故障下的作用，提出了撬棒动作后不同短路故障类型下DFIG的短路电流特性；文献[12]考虑撬棒系统的动作时延后，给出了DFIG短路故障电流的全过程精确计算方法，并对其进行了验证；文献[13]针对电网电压的不同跌落情况，给出了撬棒系统的动作原则及对卸流电阻的优化；上述研究均为DFIG的电流保护提供了理论依据。然而，文献[14-15]的研究指出，撬棒电阻投入后，由于DFIG的进入了异步模式，其正、负序阻抗在不对称故障时将可能不再相等，从而使上述基于正、负序阻抗的电流计算方法产生较大的误差，进而影响保护方案的有效性。文献[16]也通过仿真与录波分析验证了不对称故障下DFIG正序阻抗可能会出现大于负序阻抗的事实。

正、负序阻抗的不相等将使传统的基于序阻抗相等的自适应电流保护[17]在双馈型风电场的汇流集电线速断保护应用中面临着巨大挑战。为了改善上述情况，本文首先基于不对称故障下DFIG的阻抗与转速率函数关系，分析了DFIG正、负序阻抗的变化特性；然后据此提出了一种改进电流速断保护方案及其整定方法；最后，通过PSCAD仿真平台中的双馈型风电场模型对所提理论与保护方法进行了验证。

1 撬棒动作后的DFIG序阻抗特性及其影响分析

1.1 撬棒动作后的DFIG序阻抗特性

图1为DFIG内部结构及撬棒动作后的序阻抗等效电路。

图1 DFIG内部结构及撬棒动作后的序阻抗等效电路Fig.1 The internal structure and sequence impedance equivalent circuit based on the crowbar system of DFIG

图1a给出了含撬棒系统的DFIG内部结构，主要包括双馈发电机、背靠背换流器、撬棒系统电路、齿轮箱及风力机等部分。当保护系统监测到双馈风机交流端口电压降低时，由于低电压穿越的需求，撬棒电路投入运行系统，转子侧换流器闭锁以保护开关器件。由于上述过程通常在5 ms内完成[17]，因此并不会触发线路的保护动作。

撬棒电路动作后，DFIG系统将等效为转子侧带电阻的异步电机[18-20]，此时，对于不对称故障，DFIG的正、负序等效电路将分别等效为图1b，其中，Rs，Rr分别为定、转子侧的等效电阻；Xsσ，Xrσ分别为定、转子侧的等效漏抗；Xm为励磁电抗；Rc为撬棒电阻；s为转差率。上述参数均为归算到定子侧的参数。

基于图1b可知，撬棒动作后DFIG的正、负序阻抗可以分别计算为下式：

因此，正、负序阻抗的具体大小与相位可以表示为下式：

式中：Z1为DFIG的正序阻抗；Z2为DFIG的负序阻抗。

考虑到对于任意DFIG，其内部参数是确定的，因此根据式（2），DFIG的正、负序阻抗只与转差率s有关。考虑到DFIG的转差率s通常在[-0.35，0.35]之间[15]，根据式（2）可知，DFIG正、负序阻抗随转差率的变化曲线如图2所示（基于文献[21]中的DFIG参数）。由图2可知，由于撬棒电路卸流电阻与转差率的影响，DFIG的正、负序阻抗并不相同，且正序阻抗要大于负序阻抗。同时，正序阻抗受转差率影响较大，负序阻抗则比较平稳。基于式（2）可知，上述结论对于含撬棒系统的DFIG具有一般性。

图2 撬棒动作后的DFIG正、负序阻抗大小分析图Fig.2 The sequence impedance analysis of DFIG

1.2 撬棒动作后DFIG正、负序阻抗不等对汇流集电线传统自适应电流速断保护的影响分析

图3给出了基于DFIG的双馈型风电场典型结构，主要包括以下部分：并联风电机组、35 kV汇流集电线、升压变以及高压送出线。对于35 kV汇流集电线，传统的自适应电流速断保护（保护1～保护N）假定了DFIG的正、负序阻抗相等，且转差率为0（或接近于0），因此其整定值（以保护1为例）为

图3 双馈风场典型结构Fig.3 The typical structure of DFIG-based wind farm

式中：Krel为可靠系数，Krel＞1；Kt为故障类型参数，三相故障时Kt=1，相间故障时；Ė为并联DFIG机组的等效电动势；Z1e为并联DFIG机组的等效正序电抗（转差率在0附近）；Z汇线1e为汇流集电线1的等效阻抗；I汇线1末_正=负为假定DFIG正、负序阻抗相等时的汇流集电线1末端发生故障时的流过保护1的电流。

然而，由1.1节的分析可知，发生不对称故障时，并联DFIG机组的正、负序阻抗并不相等，且转差率s可能并不为0，因此汇流集电线1线路末端发生故障时，流过保护1的实际电流并不为KtI汇线1末_正=负，而是：

式中：Z1e.实际，Z2e.实际分别为并联DFIG机组实际的等效正、负序电抗。

由于DFIG的正、负序阻抗以及汇流集电线的阻抗均为感性电阻型，且根据1.1节的分析可知转差率不等于0时的正序阻抗值均小于转差率等于0时的正序阻抗值，负序阻抗值始终小于正序阻抗值，式（4）中两个电流的关系为

也就是说，若令I汇线1末_实际=Iset.传统，则此时的故障点应在汇流集电线的末端以外。

以图3的双馈型风场为例进行分析。在传统的自适应速断保护中，由于未考虑到实际正、负序阻抗变小使故障点的电流变大的影响，便可能出现故障点F2故障，保护1～保护（N-1）全部动作，致使整个风电场全部脱网，造成故障的扩大。因此为了避免撬棒动作后DFIG序阻抗特性造成传统自适应保护的无选择性，需要根据实际的故障电流情况，提出新的适用于双馈型风场的改进自适应保护方案。

2 汇流集电线改进自适应电流速断保护的整定及实现

根据图2的分析可知，虽然撬棒动作后DFIG的正、负序阻抗不等，但正、负序阻抗的大小在故障期间基本是稳定的（故障期间转差率s的变化缓慢，可以认为是不变的），因此在自适应保护中，可以利用故障时的序网络在线计算DFIG的正、负序阻抗[22]，并将其应用到保护值的整定中。

通过在线计算的并联DFIG机组正、负序阻抗Z1e_cal，Z2e_cal，双馈型风场汇流集电线的改进自适应保护值可以计算为

式中：Krel.改进为改进自适应保护的可靠系数，Krel.改进＞1。

通常情况下为了保护85%～90%左右的配电线路长度，并避免保护整定过程中计算误差、互感器误差以及继电器动作电流误差造成的影响，且保留一定的整定裕度，取值为1.05～1.15。Kt.改进为改进自适应保护的故障类型参数，Z1e为转差率为0时的并联DFIG机组的等效正序电抗。

基于式（6）的整定原则，详细的改进自适应保护方案流程如图4所示。

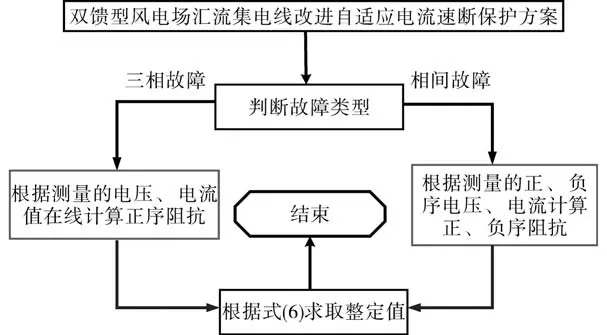
图4 改进自适应电流速断保护整定流程Fig.4 The flow chart of setting principle of improved adaptive instantaneous overcurret protection

由图4可知，改进自适应电流速断保护的关键在于正、负序阻抗值的实时在线计算以及对保护整定值的系数修改，从而使保护系统可以根据负序阻抗的减小情况，合理的增大整定值，保证保护动作的选择性。上述故障期间的实际测量值之所以可以被应用于式（6）的原因如下：目前的兆瓦级DIFG的转动惯量均较大，因此故障前后风机的转差率变化可以被忽略，从而使故障期间的正、负序阻抗也基本不变。

3 基于PSCAD的仿真验证

为了对本文所提的改进自适应电流速断方案进行验证，在PSCAD仿真平台中搭建了一个与图3结构相似的模型，其中包含10个并联DFIG机组，假设每个并联DFIG机组均具有相同的参数，且每个并联机组均包含10个DFIG，每段汇流集电线的长度均为4 km，每个DFIG的具体参数如表1所示。

表1 仿真参数表Tab.1 The table of simulation parameters

图5给出了汇流集电线1末端发生AB相间短路（故障持续0.2 s）时DFIG的正、负序电流、电压、阻抗以及关键电气量的仿真结果波形图。

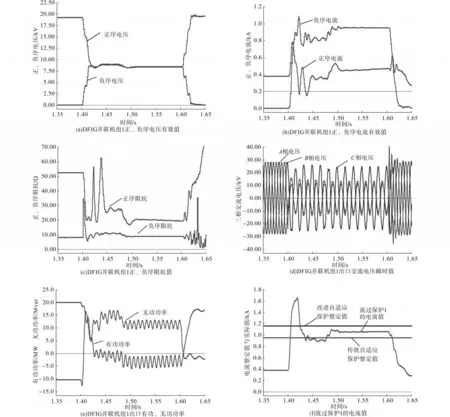
图5 汇流集电线1末端AB相间短路仿真结果Fig.5 The simulation results of short-circuit fault between AB phases of the end of the collector line 1

由图5a可知，1.4 s时汇流集电线1发生A B相间短路。在此之前DFIG正常运行，且出口处并不存在负序电压；1.4 s后由于发生了相间短路，DFIG的正序电压有效值下降，同时相间不对称故障在故障点产生相应的负序电压。负序电压引起了电路中负序电流的产生，同时正序电流也由于短路故障时系统正序阻抗的减小而产生了相应的增加，如图5b所示。图5c给出了故障发生后，DFIG的正、负序阻抗值，从中可知，负序阻抗明显小于正序阻抗，这与理论分析是一致的。同时，不相等的正、负序阻抗也是不对称故障时传统自适应电流速断保护出现误动作的主要原因。

图5d给出了汇流集电线1末端发生AB相间短路时DFIG的交流端口电压仿真波形。从仿真结果可知，当汇流集电线末端发生AB相间短路时，A，B相的电压幅值将降低，触发撬棒系统动作，DFIG进入低电压穿越阶段，有功出力逐渐下降，如图5e所示。同时，当持续时间为0.2 s的相间故障消失后（1.6 s），撬棒系统退出，系统重新恢复正常，有功传输功率重新上升至稳态值，风机系统成功完成了低电压穿越。

图5f给出了汇流集电线1末端发生AB相间短路时不同自适应电流速断保护的整定值（可靠系数采用了Krel=Krel.改进=1.1的参数值）与实际故障电流的关系。从中可知，对于集电线1上的保护1而言，故障前流过的电流为380 A，故障后流过的电流则为1 050 A。同时，根据式（3）与式（6）可以得到保护1在传统自适应保护与改进自适应保护下的整定值分别为950 A与1 155 A。对比上述3个电流值可知，仿真场景下的故障电流将引起传统自适应保护下的保护1出现误动作，使保护系统失去选择性（电流速断保护只保护85%～90%左右的线路长度，线路末端故障，速断保护应不动作）。也就是说，传统自适应电流速断保护下的DFIG此时已经失去了低电压穿越能力。而在本文所提的改进自适应保护中，由于整定值根据负序阻抗的降低进行了相应的提高，保护1并未达到动作值，保证了保护系统的选择性，提高了DFIG的低电压穿越能力。