安全可靠性约束下的微电网电能最优调度模型设计研究

傅予，李铁

（国网辽宁省电力有限公司，辽宁 沈阳 110000）

随着国家对电网项目的不断重视和发展，配电网改造和新建项目日益增多，而以主动配电网为形态构建的微电网对电能调度也提出了极高的要求。只有不断提高电力系统的环保、经济等状况才能适应电网结构和功能日益发展的趋势。若要实现微电网和主动配电网的良好发展，需要解决日益增长的能源需求与能源匮乏的冲突、能源污染与环保的冲突；增强电力能源利用率、优化能源分配；为电网的发展营造一个安全高效的环境[1-2]。

以解决上述问题为目的，首先，合理安排电力燃料种类、污染物分解、电网安全等要素，实现电力发展环境最优化。其次，电网供电质量和供电安全性等问题得到部分缓解，依赖于分布式电源以微电网形式融入到大电网中。但微电网优化模式日益繁琐，导致可再生能源存在随机性以及间歇性的弊端，这些缺点使得微电网调度方法以及控制策略的研究增加了难度[3]。基于这些因素，为了实现微电网电能的最优调度，设计一种考虑安全可靠性约束下的微电网电能最优调度模型。

1 安全可靠性约束下的微电网电能最优调度模型设计

1.1 微电网电能优化调度多目标模型构建

位于孤网状态下的微电网，既要做到排污量和运行成本最低，又要符合热电负荷的规定以及其内部单元的运转模式。位于并网状态下的微电网，解决好与大电网潮流双向流动以及电能互购等难题是关键[4]，也要顾及上述的影响因素。设计的微电网系统电能优化调度公式为

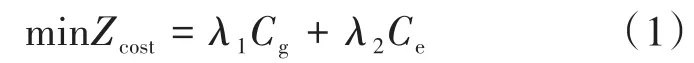
式中：Zcost，Cg，Ce分别为微电网总费用、系统发电价格和污染气体排放罚款成本；λ1，λ2分别为Cg，Ce的权重系数。

经分析可知，发电成本以及排污罚款成本是微电网系统运行成本的主体。根据经济杠杆原理，来探究不同要素对发电成本的影响程度，影响越大其权重比例就越大，则0≤λ1，λ2≤1。

1.2 微电网安全性与可靠性约束分析

1.2.1 节点电压安全裕度

通过控制节点电压的方式来促进微电网系统内部元件的稳定运转。文章用电压安全裕度来描述微电网安全性指标[5]，即微电网最低电压偏差安全裕度以给定的置信水平要求。

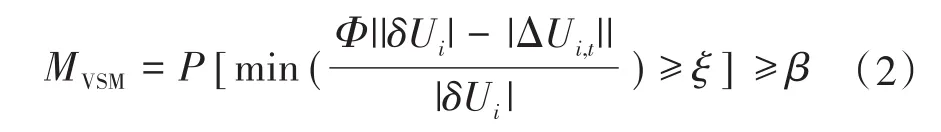
式中：MVSM为最低电压偏差安全裕度；P为调整系数；ΔUi,t，δUi分别为 t时段节点 i的电压偏差量与其允许的最大节点电压偏差，文章取δUi为额定值的-8～+5%；ξ，β分别为电网安全裕度的门限值、电网节点电压安全裕度的置信水平；Φ为0-1状态变量，具体公式如下：

1.2.2 供电可靠水平

基于微电网的弊端引起高估系统出力，为实现系统安全牢固，文章将失负荷概率看成微电网供电可靠指标，也就是系统总负荷的功率始终大于微电网系统总输出功率[5]。所以，用系统失负荷概率PLOLP以给定的置信水平要求来描述处于未知状态的微电网供电稳定性：

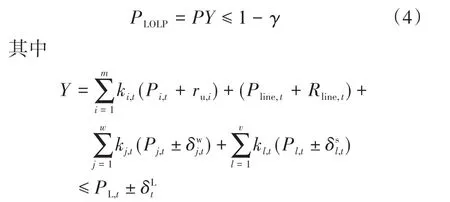
式中：γ为微电网系统真实性的置信水平；m，w，v分别为微电网中可控机组、风力发电机（wind turbine，WT）以及光伏电池（photo voltaic，PV）的数目；ru,i为i个可控机组爬坡率的最大值；Pline,t，Rline,t分别为t时段中微电网向低电压配电网（distribution network，DN）购电电量以及旋转待用容量；kx,t为从（0，1）之间任意选取的状态变量，其用于描述t时段分布式电源（distributed generation，DG）是开启还是闭合，x=i，j，l；分别为该时段负荷预测误差、WT以及PV出力误差；Pi,t，Pj,t，Pl,t，PL,t分别为t时段可控机组、WT，PV以及负荷预测值。

1.3 考虑安全性与可靠性的微电网经济调度

1.3.1 多目标模型中各分量的求解

1）系统发电成本Cg。燃料费用、运行维护费用、和大电网交互电能的费用共同构成了隶属于微电网各单元的发电成本。因此这几项也是微电网系统的发电成本。则

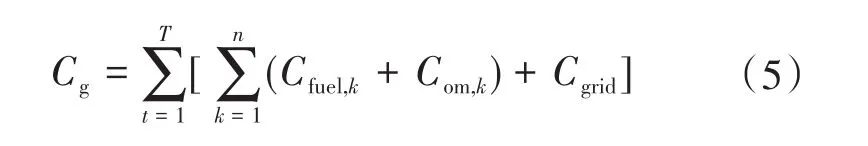
式中：n为处于微电网内部的分布式发电单元量；T为小时数；用 Cfuel,k，Com,k，Cgrid分别为第k个分布式单元的燃料费用、运行维护费用以及微电网与大电网的交互费。

2）系统燃料成本Cfuel。新式环保的风力以及光伏发电方式具有无污气排放、无燃料费用的优势，通过采用这两种方式来减少发电成本。所以，除了计算微型燃气轮以及燃料电池在发电时所需燃料成本以及维修费用，再加上两种发电方式的功率消耗即可[6]。下面公式描述了燃料成本的计算方法：

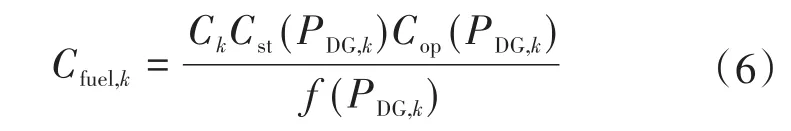
式中：PDG,k，Ck分别为第k个分布式单元的功率消耗以及燃料费用；f(PDG,k)，Cst(PDG,k)，Cop(PDG,k)分别为第k个分布式单元的所需燃料、机组启动所需燃料以及运转阶段所需燃料费用。

3）设备的运行维护成本Com。机器开关费用、人工费用、网络消耗等构成了微电网设备运行的维护成本，一般来说，微电网设备运行成本与电能的形成用以下公式描述，两者是线性关系[7]：

式中：ζk为第k个分布式单元设备的运转费用消耗。

4）与大电网电能交互成本Cgrid。处于并网运行模式使得微电网可以在短缺电能的情况下向大电网索取电能，在自身正常运转又有多余电能的情况下，向大电网出售电能，为微电网的运行提供了极大的便利[8]。两者的电能交互成本用下式表示：

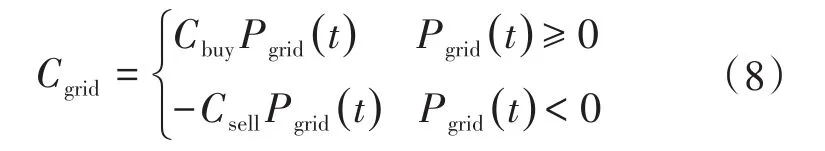
式中：Pgrid，Cbuy，Csell分别为微电网与大电网的交互功率、微电网从大电网购电价格以及向大电网售电价格。

5）污染气体排放罚款成本Ce。基于部分发电单元在产出电能的阶段里，释放污染性气体使得生存环境遭到破坏，我国出台了关于污染物排放的罚款政策，采用分析不同发电单元产出状况的方式算出关键性污染物的释放量。碳化物、氮化物、硫化物是排放气体的主要污染源[9]，所以罚款费用主要来源于此类污染物的排放。以下公式表示微电网发电污染气体处罚费用：

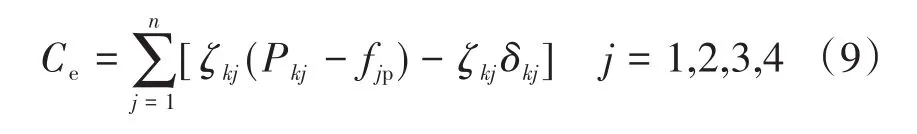
式中：ζkj为第k个分布式单元第j种污染物处罚系数；fjp，δkj分别为第j种污染物处罚费用率以及污染物数量种类；Pkj为第k个分布式单元第j种污染物估计电量费用率。

1.3.2 约束条件

微电网运转既要符合式（2）～式（4）又要执行如下规则，以实现其高效便捷安全的运转[10]。

1）DG出力约束：

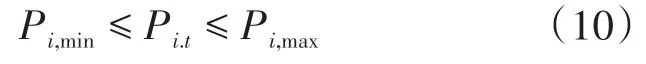
式中：Pi,max，Pi,min分别为第i个DG出力上、下限。

2）微电网功率平衡约束：

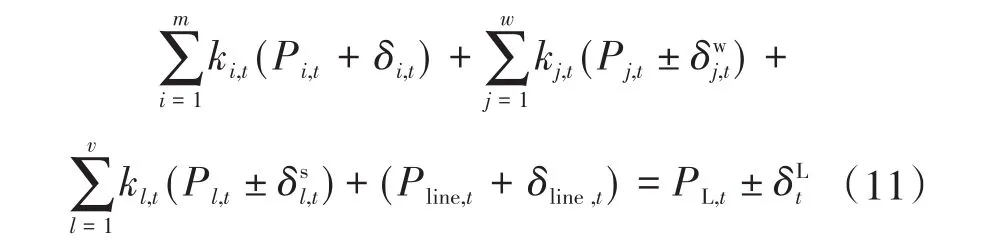
式中：δline,t为t时段DG与微电网交换功率的调整量。

式（11）中δline,t与Rline,t满足条件δline,t≤ Rline,t。

3）微电网与主网联络线传输功率约束：

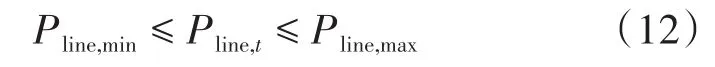
式中：Pline,max，Pline,min分别为联络线传输功率的上、下限。

4）可控机组爬坡率约束：

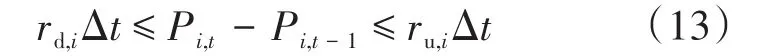
式中：rd,i为i个可控机组爬坡率的最小值；Δt为可控机组爬坡的时间。

5）输电线路传输功率安全约束。通过将各单元输送功率控制在允许的最高点以下的方式，使得电能传输高效、平稳地进行[6]：

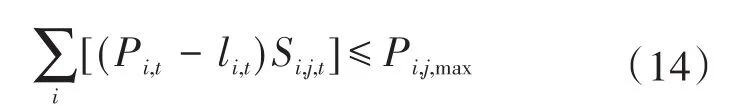
式中：Pi,t为节点i在第t时段内的功率；li,t为支路i—j可接受输出功率的最高点功率；Pi,j,max为支路i—j支路上的最大传输功率；M为微电网总节点量，满足i≤M条件；Si,j,t为在t时段内节点i输入功率对i—j的灵敏度。

1.3.3 基于PSO-BF算法的微电网能量优化调度

采用粒子群-细菌觅食算法（particle swarm optimization-bacterial foraging，PSO-BF）修正粒子速度和位置，在避免粒子早熟收敛的情况下，构建微电网电能最优调度模型。考虑系统发电成本、燃料成本、设备运行维护成本、同大电网运行交互成本以及污染气体排放罚款成本，对微电网电能调度问题进行优化求解[10]。

粒子群算法能迅速找到解决问题的最佳方式，细菌觅食算法有利于细菌各分子通过趋化阶段发掘最近范围内的最佳值，防止最佳解所处范围被细菌过滤掉的现象[11]。所以，粒子群-细菌觅食算法是细菌觅食算法有发展规律的趋化过程，融入到粒子群算法进行部分查找阶段，不仅改进了粒子群算法与细菌觅食算法的弊端，又实现了此算法快速、高效、目标明确的工作状态，改善了局部查找的功能。

PSO-BF算法修正粒子速度和位置表达式为

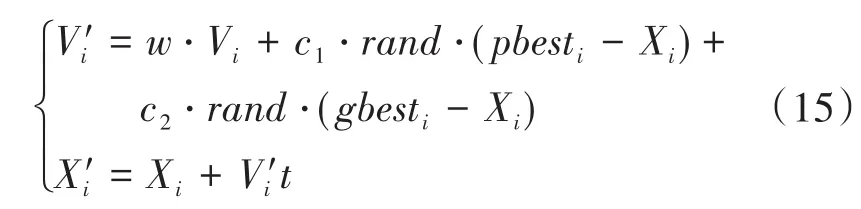
式中：V＇i，X＇i分别为修正后的速度和位置；Vi，Xi分别为粒子原速度以及位置；t为某一时间段；w为粒子速度环境影响系数；pbest，gbest分别为各粒子的最佳位置以及种群内全部粒子的最佳位置；c1，c2分别为pbest，gbest粒子的学习因子；rand为0或1变量。

以下公式描述了PSO-BF的修正过程：

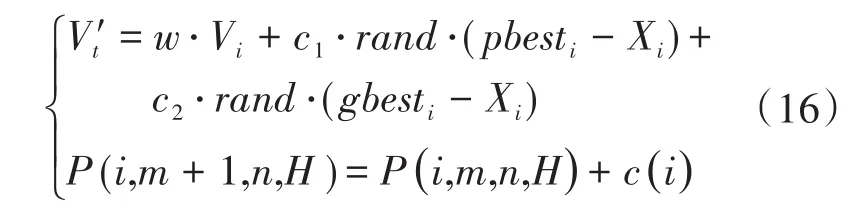
式中：P（i,m+1,n,M）为粒子i在第m+1代趋向第n代繁殖的位置；P（i,m,n,M）为粒子i在第m代趋向第n代繁殖的位置；c()i为步长；H为最大迭代次数；m为翻转次数；n为趋化次数。

将PSO-BF进行反复运算。假设有这样一个球，其半径用ε来表示，球心用粒子整体最佳位置gbest来表示，Xi到球心的长度用D来描述。文章采用以下公式来避免粒子早熟收敛的现象：

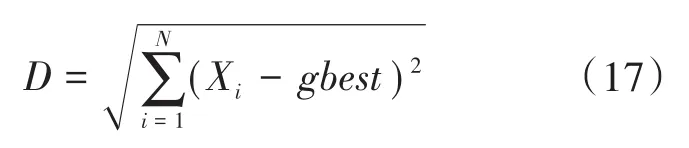
式中：N为现有的粒子量。

当粒子i在球里面时，则D＜ε。

设置M表示球内的粒子量，esp表示可接受的粒子处于球内概率的最大值，则有：

1）可随机将球内的粒子分布到空间，应满足M/N＞esp的条件。

2）不能将球内的粒子分布到空间，应满足M/N＜esp的条件。

下文对PSO-BF算法如何进行微电网优化调度求解进行了详细的描述：

1）将分布式电源的出力、负荷、风速等数据进行还原设置，重新定义PSO-BF算法的规模大小、最大迭代次数、翻转次数以及趋化次数分别为s，H，m以及n。

2）求解即刻全局以及个体最佳的分布式电源出力gbest，pbest时，应采用目标函数对粒子的适应度值实施评估，同时通过公式（16）对分布式电源出力进行修正。

3）对完成修正的粒子i适应度J( )i,m同粒子动态波动时的最佳适应度值，以及翻转次数m值，是否趋近于阈值动态变化次数Ns，如果存在J(i , m )＜Jlast和m＜Ns，粒子应持续变化，再进行修正，否则运行过程4）。

4）观察趋化次数n是否超过最大趋化迭代次数Nc，若超过，执行5）；若没超过，执行2）。

5）采用式（17）得到各粒子到gbest的长度D，然后决定是否分散粒子。

6）通过公式（15）来修正粒子的速度、位置等数据。

7）观察迭代次数H是否超过最大迭代次数Iter的上限，若超过，执行8）；若没超过，执行2）。

8）最后得到整体的最佳解也就是微电网机组的最佳出力，实现微电网电能的最优调度，得到微电网电网最优调度模型为

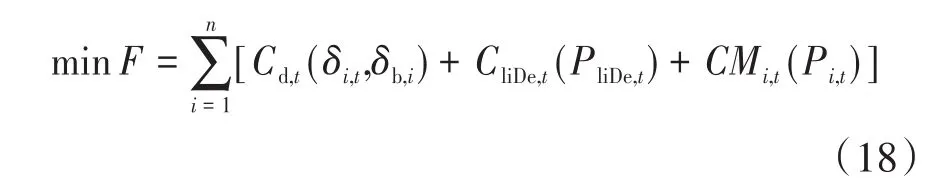
式中：Cd,t为t时段微电网出现的交换费用；δi,t为t时段可控机组i的维护费用；δb,i微电网运行费用；CliDe,t为最大允许目标函数偏离程度；PliDe,t为微电网机组运行效率；CMi,t为机组i在第t时段的功率最大值；Pi,t为机组i在第t时段的负荷功率。

2 实验分析

2.1 运行成本检测

为了验证改进调度模型的有效性及可行性，实验以PSO调度模型[12]、机会约束调度模型[13]和上文中PSO-BF调度模型下的某微电网运行成本为基础进行实验分析。

表1为不同调度模型下微电网运行成本表。分析表1数据可知，PSO调度模型的燃料成本远远高于其它两种调度模型，并且运行维护成本和污染罚款也高于其它两种调度模型。机会约束调度模型和PSO-BF调度的电能交互结果是负数，说明两种模型实现了同主网的交互融合，微电网通过向主网出售多余的电能的方式获得部分收入，使得总的发电成本比PSO调度模型低，并且PSO-BF调度模型的总发电成本最低。因此能够得出，PSO-BF调度模型下的实验微电网运行成本最低，模型调度效果最佳。

表1 不同调度模型下微电网运行成本Tab.1 Operation cost of microgrid under different scheduling models

系统在孤网运行情况时，热电功率平衡仅能从微电网内部供给，实验从经济性能最大化出发，得到本文调度模型的优化结果用图1和图2描述。

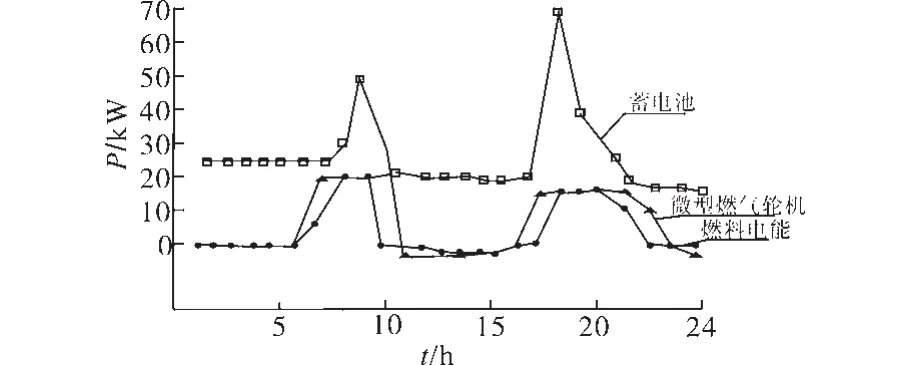
图1 不同发电设备负荷总功率分析Fig.1 Analysis of load total power with different power equipments

图2 微型燃气轮机蓄电池SOC变化趋势Fig.2 SOC change trend of micro gas turbine battery

由图1可知，0～7 h中，本文调度模型下的实验微电网负荷总功率低于新能源发电功率，有部分能量残存，因为蓄电池能量已经饱和，所以剩余能量只能使用卸荷负载删除，7～10 h中，新能源电量不够充分，应及时使用蓄电池放电进行补充，补充不充分的部分根据发电成本最小化按顺序启用燃料电池、微型燃气轮机发电。

由图2可知，在7～10 h，蓄电池SOC降低，主要是由于电能负荷需要增大，蓄电池输出电能用于补贴电能负荷；在10～13 h中，新能源电能在保证负荷的同时剩余能量将补充蓄电池，蓄电池SOC提高。13～15 h中，假使蓄电池的持续供给量如破容量限制，则充电暂停，在15 h以后，蓄电池输出电能，蓄电池的SOC下降。综合分析这些结果说明，本文调度模型实现了配电网的优化调度，确保微电网电能变化的平稳性。

2.2 不同调度模型的收敛状态监测

实验检测传统基于PSO的配电网调度模型和PSO-BF调度模型在目标函数中运行20次后，两种调度模型在微电网电能最优调度过程中的收敛结果如图3所示。

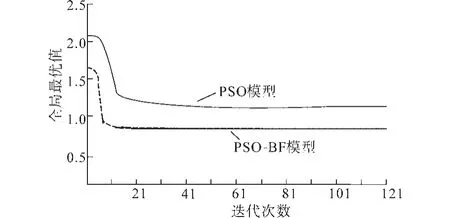
图3 不同调度模型的收敛曲线Fig.3 Convergence curves of different scheduling models

分析图3能够看出，相对于基于PSO的配电网调度模型，基于PSO-BF模型的收敛效率更高，并且收敛精度比传统方法更强。PSO-BF模型对细菌觅食算法进行了优化，提高了配电网电能调度的收敛性能。因此得知在全局搜索力和局部搜索过程中，PSO-BF模型的性能最佳，具有搜索精度准确，收敛时间短，适合全局优化的特点，实用性能强。

2.3 优化结果及分析

采用PSO-BF模型和算法进行实时优化计算。实验以文献[14]提出的微电网系统为例。实验系统由风力发电单元以及含光伏发电单元、微型燃气轮机和储能单元各一台构成，如果不同单元参数和微电网购售过程的不同峰谷电价存在一定的差异，微电网以及大电网中联络线的最大客观传输量是50 kW，设置储能单元原始SOC为60%[14]，采用PSO-BF算法和统计方法，基于Matlab脚本程序在不同的运行状态下，实施微电网系统的仿真检验实验。

设定并网运行模式1为新能源和微型燃气轮机发电，储能单元放电；并网运行模式2为新能源和微型燃气轮机发电，从电网中购电，储能单元不发挥作用；并网运行模式3为新能源发电，储能单元放电，并且将多余的电量进行出售；并网运行模式4为新能源发电，多余的电量通过储能单元进行充电。某日并网运行高峰时段的调度结果如表2所示。

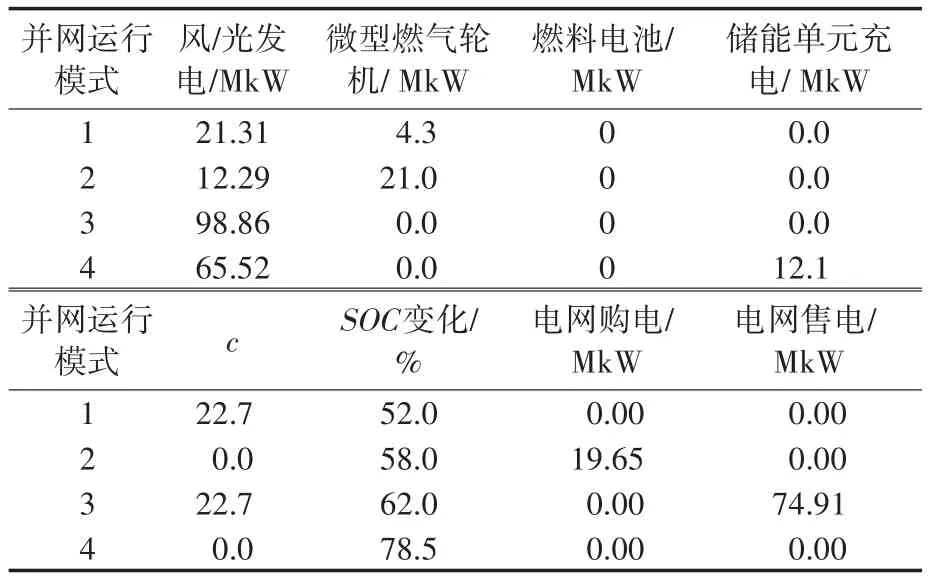
表2 并网运行高峰时段调度结果Tab.2 Dispatching results of grid-connected peak hours

根据表2描述的PSO-BF调度模型在并网运行高峰时段调度结果可知：如果风能、光发电不能对负荷需求给予充足能量时，假使储能充分，储能单元则对缺额电能进行及时补充，可控为电源相对出力；假使储能不满，不能对储能单元实施充电，则微型燃气轮机及时对缺额电能进行补充，此时应向电网购电，并完成燃料电池的发电；如果风能、光发电量未到达最低值，则PSO-BF模型不再调控微电源出力；如果微电网中电能量未达到最低值，则PSO-BF调度模型放电向电网售电；假设储能不充分那么则使用剩余电量向储能单元补充电量。

设定孤岛运行模式1为新能源和微型燃气轮机发电，储能单元放电；孤岛运行模式2为新能源、微型燃气轮机和燃料电池发电；孤岛运行模式3为新能源发电，多余的电量通过储能单元进行充电；孤岛运行模式4为新能源和微型燃气轮机发电，多余的电量通过储能单元进行充电。孤岛运行高峰时段的调度结果如表3所示。

由表3可以看出，当配电网处于孤岛状态，采用PSO-BF调度模型的微电网可控微电源不必从上级电网调度电能，若风能、光发电无法提供微电网负荷需求并且储能量足够，则储能单元放电将补充所缺电能；若微电网储能缺乏，则从微型燃气机以及燃料电池获取电能；当以上仍不能达到符合需求那么将依照等级减载。在风能、光发电足够充分时，剩余电量将对储能单元充电，在此基础之上的剩余电量会作用与小光伏单元出力。

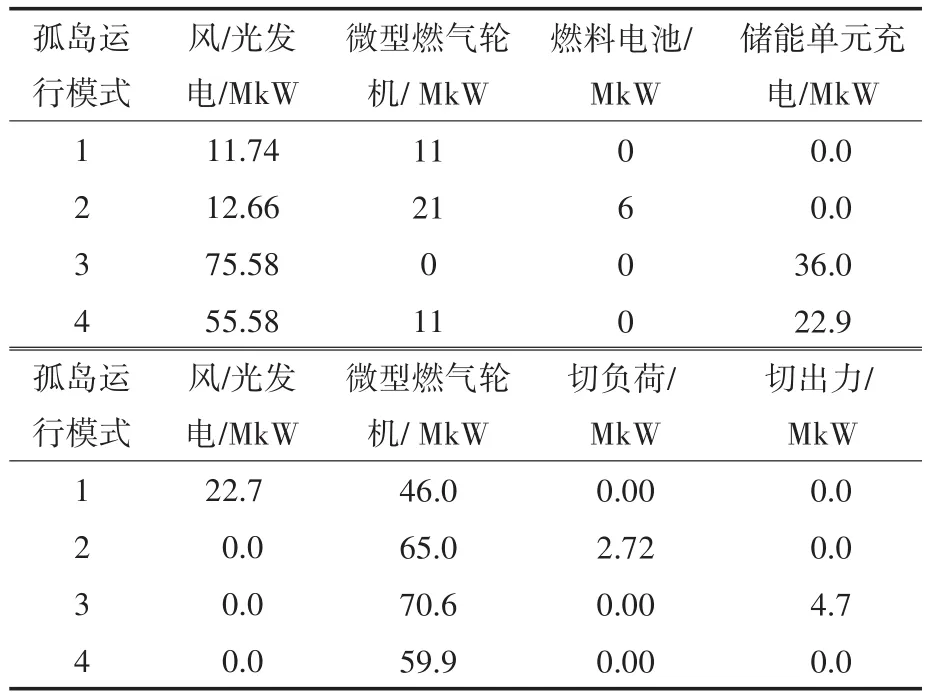
表3 孤岛运行高峰时段调度结果Tab.3 Dispatching results of islanding operation during peak hours

实验检测PSO-BF调度模型的全天调度结果时，在上文中风力发电、光伏发电以及负荷24 h整点估计信息的基准上，假设三者间隔是5 min，1 d的运动信息，采用并网双向功率流动模式的模拟统计得到的微电网的实际负荷作为评估标准，统计PSO调度模型和PSO-BF调度模型的实时调度交互功率以及日供电成本分别如图4、表4所示。

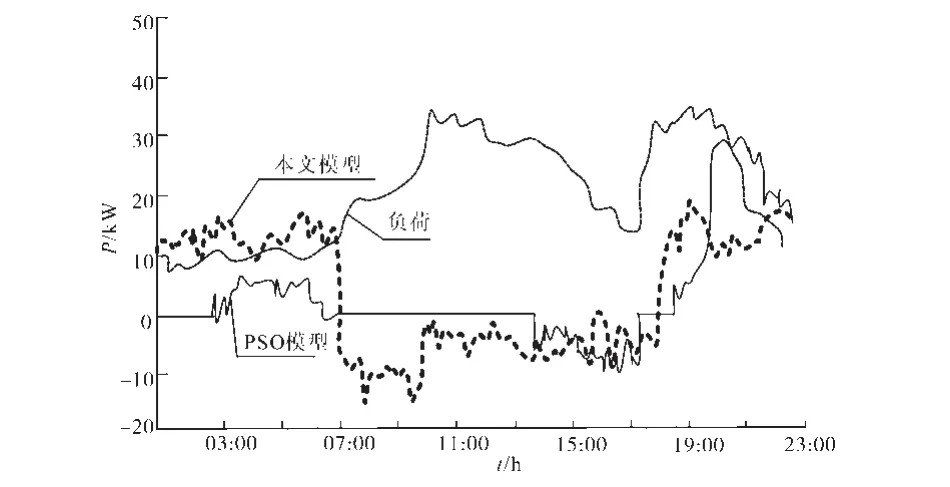
图4 微网与电网实时调度交互功率曲线Fig.4 Interactive power curves for real-time dispatching of micro-network and power grid

表4 采用PSO-BF模型与PSO模型下实时调度日供电成本Tab.4 Using PSO-BF model and PSO model to dispatch daily power supply cost in real time

分析图4可得，在7 h以内，本文模型的实时调度交互功率较大，随后出现下降，在7～17 h表现相对平稳，此后出现较大增幅。本文模型相对于PSO模型，在峰平时段对电网供电更有利，可有效起到平峰填谷的效果。

从表4可看出，PSO模型下微电网实时调度每天供电成本是44.28元，PSO-BF模型下微电网实时调度日供电成本是28.36元，每天供电成本比PSO模型降低15.92元，使成本降低到30%之多，说明PSO-BF调度模型具有较高的经济价值。

3 结论

文中设计了一种安全可靠性约束下的微电网电能最优调度模型，该模型采用PSO-BF算法修正粒子速度和位置，在避免粒子早熟收敛的情况下，构建微电网电能最优调度模型。可确保管理人员在谷时段通过储能单元实施充电储能，在峰平时段对电网供电，可以起到平峰填谷的效果。同时，实现了微电网的安全可靠性以及节能环保控制，提高了微电网总体调度质量。