一种不同色域空间下的无监督图像分割技术

吴 涛， 王伦武， 王伦文， 朱敬成

(国防科技大学电子对抗学院，合肥，230037)

图像分割一直是计算机视觉领域研究的重要内容之一，通过对图像中的像素根据其共有特征进行分类，从而实现对不同的物体进行分割，在无人驾驶、人机交互和医学等领域[1-2]具有重要应用。

对图像的分割方法大多是基于深度神经网络的方法[3-5]进行端到端的有监督训练，能够自动学习图像的特征，分割的精度很高，分割效果较为理想。与此同时，其耗费时间长，训练样本标记成本高，而且神经网络的训练往往需要大量的高质量样本作为输入数据集，这些问题的存在成为分割技术在部分领域落地应用的一大阻碍。

由此一些无监督的图像分割方法被提了出来[6]。文献[7]提出了一种元学习的方式进行图像分割，通过探索特定视觉效果的网络丰富图像，以无监督的方式学习视觉效果的内部表征，并利用这一知识来区分出图片中的不同含义。文献[8]提出的深度模型，通过完全无监督的方式，将两个完全卷积网络连接到自动编码和解码器中，并进行包括条件随机场平滑和分层分割等后处理，在Berkeley分割数据集上取得了良好的分割结果。文献[9]提出了一种基于深度图像聚类的无监督分割框架，由特征变换子网络和可训练深度聚类子网络组成，在现有的网络架构基础上，通过迭代更新簇与簇之间的关联和簇中心来分配不同簇数的像素。在Berkely数据集上同样展现了良好的分割性能。文献[10]提出了一种两步自监督域自适应方法，使用基于熵的排序进行模型的域间自适应，该方法在大量数据集上取得了较好的分割效果。文献[11～13]则都是在形成超像素的基础上对输入的图像进行超像素分割，实验中都展现出了良好的分割性能。

本文针对数据集中目标与背景高度融合的特点，为了提高对一些伪装特性的识别效果，在不同色域空间上对图像分割进行了实验。利用机器学习分割方法对图片进行预分割，形成空间上连续的超像素结构，并结合深度神经网络良好的特征提取能力，在预分割的基础上，对像素进行再次聚类，最终实现分割的效果。

1 色域空间转换理论及方法

1.1 不同颜色空间及其转换

颜色空间实际上是一个三维模型，在颜色的三维空间中，不同的坐标对应着不同颜色。

RGB颜色空间利用三基色红绿蓝作为基准色，通过不同的比例进行叠加混合而成，是根据人眼识别物体的颜色而定义，因此对人类感官的分辨比较友好，见图1。

图1 RGB颜色空间

在RGB颜色空间中，大部分颜色C都可以用rgb分量表示出来：

C[r,g,b]r,g,b∈[0,255]

(1)

HLS或HIS颜色空间是用色调、强度或明度、饱和度3个分量表示的颜色空间，能够更好地对颜色进行数字化处理，见图2。

图2 HIS颜色空间

HLS或HIS在空间上是一个圆锥模型，纵轴方向代表的是颜色亮度，RGB转HIS公式如下：

(2)

(3)

s=1-3min(r,g,b)

(4)

i=(R+G+B)/3×255

(5)

上面将HIS进行了归一化处理。可以通过式(6)的变化将HIS转化到正常的范围。

H=180h/π,S=100s,I=255i

(6)

LAB空间是通过颜色的几何度量来进行颜色区分，RGB不能直接转化到LAB空间，需要首先转换到XYZ空间，转换过程如下：

(7)

L=116f(Y/Yn)-16

(8)

A=500[f(X/Xn)-f(Y/Yn)]

(9)

B=200[f(Y/Yn)-f(Z/Zn)]

(10)

(11)

式中：Xn、Yn、Zn分别取0.950 456、1.0、1.088 754。

1.2 超像素分割方法

利用图像的颜色、纹理和亮度等浅层特征，将图像分割成在空间上连续的不规则像素块，这种分类的方式是一种粗糙分类，形成的不规则像素块也被称为超像素。超像素是一类像素的集合，形成超像素的方式有slic，felzenszwalb和quickshift等方式。

slic是基于k均值聚类，利用一组带有坐标的五维特征向量，选择颜色和空间的距离度量进行迭代聚类的超像素图像分割方式[14]。felzenszwalb[15]是一种最小生成树的聚类算法，felzenswalb算法并不需要指定算法的聚类个数，会在分割的过程中根据像素的均值不断进行迭代运算，并不断进行合适的分割。quickshift[16]是一种基于寻模的聚类方法，该算法将所有的点连接成一棵树，将每个点都移动到距离最近的高密度邻域，增加Parzen密度估计[17]，从而实现邻近区域的分割，具有很好的边界黏附性[18]。

2 分割模型与算法

深度神经网络能够挖掘图像的深层次特征，捕捉到图像的其他细节特征。结合神经网络和机器学习方式，将基于机器学习粗分类的结果作为标签值，输入到神经网络中进行特征的进一步划分，能够提高模型的分割精度。文献[19]采用了slic算法进行了区域的初步划分，形成了超像素。本文实验采用了felzenswalb和quickshift超像素分割方法，并在图片进入网络训练之前进行颜色空间的转换，在大量数据集上进行实验后发现，改进的方法具有更高的精度和更少的平均用时。图3为用于训练的神经网络模型。

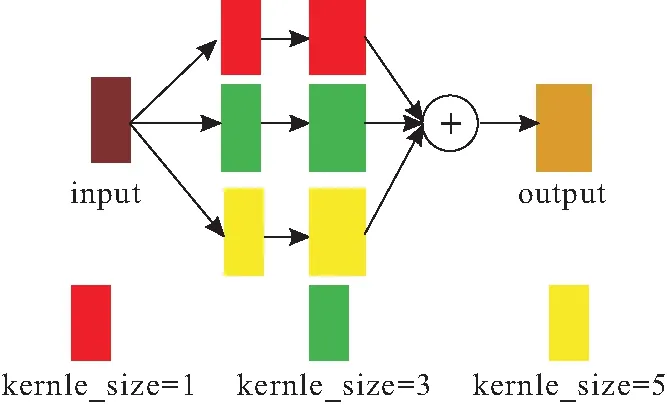
图3 深度神经网络模型

模型的输入是维度为(3,256,256)的彩色图像，分别经过1×1、3×3、5×5的卷积进行卷积运算，利用不同尺度的卷积层进行特征的提取，最后对提取到的特征进行融合，得到模型的输出结果。

算法流程如下：

输入：input=I #输入RGB图片

输出：output=O #输出语义分割结果

labels=skimage.segmentation(img) #传统的机器学习方法得到粗分类标签

model =Model() #神经网络初始化

for epoch in epochs:

output=model(image)

target=argmax(output) #根据神经网络训练结果，去数值最大者为相应元素的标签

loss=Cross_entropy(output, target) #交叉熵损失函数

optimizer.SGD(model.parameters) #优化器进行迭代计算

模型实施细节见图4。在图4中，原图片在进行了不同颜色空间转换后，分为了2个步骤来实施。机器学习分割算法对输入的数据形成初步分割结果，然后将图片数据送入神经网络中进行训练，通过对不同通道索引出该像素点最大值，得到该像素点的数值标签，通过在预分割基础上进行比较，形成更加精细的微调结果，在设置的标签范围内进行迭代循环，并得到最终的训练结果。

图4 无监督分割模型

3 实验过程及结果分析

3.1 实验条件设置和数据集

实验计算机配置如下：Inter(R) Core(TM) i7-9700 CPU @3.00 GHz, GeForce 1060Ti GPU(6 GB 显存)的Windows操作系统。实验采用pytorch架构，在训练过程中，采用SGD优化器进行优化，采用交叉熵损失函数进行参数反向传播。

本次实验采用公开的图像数据集COD10K[20]、CHAMELEON[21]和CAMO[22]进行无监督实验，该数据是包含了海洋、陆地、天空等空间，具有十分丰富的物种类别，图像构成复杂，背景元素较多，对分割来说具有很大挑战。

3.2 损失函数和评价指标

实验采用交叉熵损失函数，表达式如下：

(1-yi)log(1-pi)]

(12)

采用F1测量作为对单张图片分割精度的衡量指标。F1测量值是PR曲线的一个平衡点，F1越大，训练模型的性能越好，计算表达式如下：

(13)

式中：P是准确率；R是召回率。

3.3 实验及结果分析

3.3.1 传统算法粗分类

传统的分割算法可以根据图片中物体的颜色、纹理和亮度等特征，对图片中像素进行初步聚类，形成大块区域的超像素图像，但简单通过浅层特征进行分类十分容易产生像素分类错误的现象。在slic、felz和quickshift经典分割算法中，对图像进行了实验，实验结果见图5～7。

图5 slic算法下的粗分类结果

图6 felz算法下的粗分类结果

图7 quickshift算法下的粗分类结果

slic是对包含了xy坐标的五维特征的k-means聚类，算法包含有多个参数，具体含义为：

1)n_segments：可选分段输出图像中标签的近似数量；

2)n_compactness(紧凑性)：平衡色彩接近度和空间接近度，数值越高，空间接近度越重，使得超像素形状更加平方。

felz算法是基于有效图的图像分割，基于图像的网络图，通过最小生成树聚类生成多通道的图像区域。

1)scale是设置观察级别，规模越大意味着分割的图像越来越小；对于RGB图像，该算法使用的是颜色空间的欧式距离进行聚类；

2)min_size是最小分割单元的。

quickshift算法通过将初始数据向量移动到具有更高能级的最近领域模态实现模式搜索。

1)ratio：介于0和1之间平衡色彩空间接近度和图像空间接近度。较高的值会增加色彩空间的权重；

2)kernel_size:用于平滑样本密度的高斯内核宽度，越高以为这越少的集群；

3)max_dist：可选数据距离的切点，越高意味着越少的群集。

在上述算法对比中，slic方法对与背景高度相似的图像分割效果相对较差，许多相邻像素都存在被错分和漏分的情况，且对数据的调整也很难对与背景高度的图像做细致的分割，说明基于k-means方法的分类效果存在局限性，通过颜色进行聚类，使得边缘像素产生了较大偏差；felz算法能够对图像做一个较为精确的分割，但受参数影响较大，在参数选取不合理时，并不能产生较为准确的聚类标签，属于不同物体的像素被归为了同一类标签；相比slic算法和felz算法，quickshift具有分割结果相对较好，从图7给出的结果可以看出，quickshift算法对物体的边缘进行了较为准确地划分，基本上将待分割物体完整的与周围环境区分开来。

3.3.2 神经网络细分类

在经过机器学习的方法粗分类之后，选取了较为准确的分割结果，将其产生的标签作为聚类的标准。然后将图像通过神经网络，利用神经网络优秀的特征提取能力，提取图像更深层次的特征，对经过传统方法分类之后的结果进行微调，做出更精准的分类。对相近且相似的元素进行合并处理，得到更接近真实物体的分割效果。为了充分体现出结合了神经网络分类算法的分割性能，在3个算法上重复进行了1 000次实验，original方法是文献[13]提出的基于slic超像素分割的方法，上述方法的基础上，使用了felz方法和quickshift方法代替slic方法进行超像素分割。实验效果见图8～9和表1。

图8 训练损失曲线

图9 不同算法的f1_score和时间分布图

表1 结合了神经网络的算法的训练耗时和f1_score

从图9和表1中可以看出，original的效果相对稳定，大部分实验结果比较集中分布在一定的区域，但总体性能与改进后的算法相比，相对差一些。基于felz的改进算法的稳定性最差，却能达到最好的分割效果，且平均用时最短，说明能在较短的时间内实现对物体的分割；基于quickshift的改进算法稳定性也相对较差，但对图片的分割效果上显得较为集中，大部分实验数据都集中到小提琴图的上层区域，体现出其良好的分割性能。

为了进一步探究无监督分割的分割效果，在不同的颜色空间进行了分割实验。不同的颜色空间之间存在矩阵的相互转换，在一定程度上，不同的颜色空间对颜色的识别度存在不同的区分，不同色彩分布图片的分割效果会有所不同。实验结果见图10～12和表2～4。

图10 结合神经网络的slic算法在不同色域模式下的性能对比

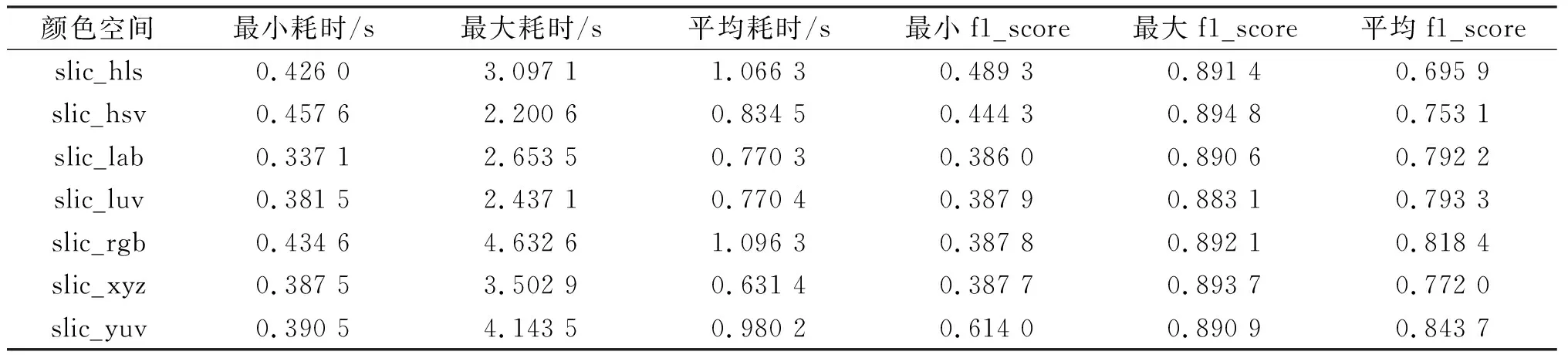
表2 结合神经网络的slic算法在不同的色域模式下耗时和f1_score

图11 结合神经网络的felz算法在不同色域模式下的性能对比

表3 结合神经网络的felz算法在不同色域模式下的耗时和f1_score

图12 结合神经网络的quickshift算法在不同色域模式下的性能对比

表4 结合神经网络的quickshift算法在不同的色域空间下耗时和f1_score

以上数据显示，结合了神经网络提取特征的felz、slic和quickshift算法在不同色域空间表现出不同的性能。在luv空间中，改进后的felz分割算法体现出较好的分割性能，而在slic算法中和quickshift算法中，则最佳的分割效果表现在不同的颜色空间。但不同的颜色空间，在不同算法中性能的体现并不具有偏向性，而是具有的不同的优势，部分颜色空间能够实现快速分割，但分割精度不是很高，部分颜色空间分割精度较高，但分割时间不稳定。

本文选取了部分图片进行了分割测试，从f1_score和训练消耗时间对算法分割性能进行评判，实验结果见图13～15。

图13 不同颜色空间的测试集在基于slic上的性能对比

图14 不同颜色空间的测试集在改进的felz上的性能对比

图15 不同颜色空间的测试集在改进的quickshift上的性能对比

可以看出，提出的算法能够进行较好的分割，且在运算时间上，大部分分割过程满足分割实时性的要求。但由于图片类型的不同和场景带来的差异，仍还存在部分图片分割时间过长、分割效果不好的情况，见图16。

图16 部分颜色模式下的分割效果

4 结论

本文针对图像分割有监督训练耗时长、训练成本高的问题，提出了在不同色域空间下对图像无监督分割方法。由于不同图像在不同颜色空间中其颜色、纹理和亮度表现出不同差异性。将图像变换到不同颜色空间，利用felz,slic和quickshift 3种经典的分割算法对图像进行粗分割，结合一个简单的神经网络模型对图像特征进行再融合、再提取，进一步提高了模型的分割性能。在CAMO，CHAMELEON和COD10K提供的数据集上进行了实验，结果表明，所提出的方法能够进行很好地分割，对单张图片的分割精度最高能达到97.31%。