基于M估计的自适应鲁棒平方根连续-离散CKF算法
2022-04-08胡浩然陈树新何仁珂汪家宝郝思冲
胡浩然, 陈树新, 吴 昊, 何仁珂, 汪家宝, 郝思冲
(1.空军工程大学信息与导航学院, 西安, 710077; 2.93184部队, 北京, 100076)
在客观物理世界中大部分动态系统均属于连续时间系统,其有间隔的测量是离散时间的,因此称之为连续-离散时间系统[1]。目标跟踪系统在本质上也是连续-离散系统,传统算法常采用的离散-离散系统模型会导致额外误差的产生。连续-离散系统的数学解算方式精度更高,状态空间描述更精确,有效提高了跟踪的性能,近几年来,已广泛应用于目标跟踪的相关领域。
为进一步提升连续-离散的滤波精度,文献[2]提出了基于容积准则的连续-离散容积卡尔曼滤波(continuous-discrete cubature kalman filter,CD-CKF)。其中,连续时间模型以随机微分方程(stochastic differential equation,SDE)表示,随机微分方程的求解是连续-离散方法区别于离散-离散方法的重要体现。文献[3]总结了基于0.5阶Euler-Maruyama方法和It-Taylor方法[2],认为其具有较高的精确度。为进一步提高状态估计的精度,高阶的数值近似方法开始被用于求解随机微分方程。文献[4]将基于非线性随机微分方程的连续模型描述为其期望和方差的模型形式,进而用高阶数值近似方法对连续模型进行了求解。在文献[5]中,基于嵌套式的隐式龙格-库塔法用于解决连续-离散扩展卡尔曼滤波(continuous-discrete extended kalman filter,CD-EKF)问题,其思想在连续-离散容积卡尔曼滤波中的应用在文献[6]中有所体现。文献[7]用自适应步长对精度完成了进一步的控制。文献[8]提出的自适应反馈算法对协方差矩阵进行预测,从而减轻了不可预知误差的影响,进一步提高了滤波的性能和效率。
以上的目标跟踪系统建立在理想条件下,但实际中各种异常条件影响着滤波的性能,模型改变、信号遮挡、信号干扰等都会导致观测站的测量异常。在文献[9]中,针对模型的不确定性提出一种基于鲁棒的CD-EKF方法,从残差范数的平方和最优的角度出发来进行优化,成功建立了鲁棒机制。但大部分鲁棒方法中将非线性问题线性化处理,引入了截断误差,进而导致精度的下降。如何应对实际问题中非线性的异常测量问题已经成为了研究热点。
本文针对异常测量,设计了一种具有鲁棒机制的非线性连续-离散跟踪算法。
1 连续-离散系统目标跟踪模型和平方根CD-CKF算法
1.1 连续-离散系统目标跟踪模型
考虑到随机扰动,连续时间目标运动模型描述为随机微分方程的形式[3]:
(1)
由随机状态的统计学知识,依据状态期望和协方差进行状态估计将有利于提高连续-离散滤波算法的精度,其随机微分方程可这样表示[7]:
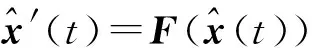
(2)
(3)
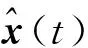
离散时间的测量模型与传统模型类似,表示为:
Zk=h(x(tk))+vk,k=1,2,…,N
(4)
式中:Zk是实际测量值;h为观测函数;假设vk满足零均值的高斯分布,即:vk~N(0,Rk);k指离散的时间点;xk指x(tk)在时间tk处的状态值。
1.2 平方根CD-CKF算法
CKF算法利用容积数值积分来逼近状态后验分布,数值精度较高,稳定性较好。为保证误差协方差矩阵的正定性和对称性,这里介绍连续-离散容积卡尔曼滤波的平方根形式。与典型的CKF方法相似,将连续-离散与容积准则相结合,同样分为时间更新与测量更新两个步骤。
1.2.1 时间更新
在平方根连续-离散容积卡尔曼滤波算法[10]中,状态容积点的定义如下:
(5)
式中:S(t)是协方差矩阵P(t)的下三角矩阵,满足P(t)=S(t)ST(t)。
因此,期望和协方差矩阵可以由容积点重新进行表示:
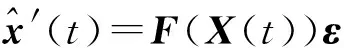
(6)
P′(t)=X(t)WFT(X(t))XT(t)+Q(t)
(7)
W和ε的含义如下:
(8)
式中:I2n表示维数为2n的单位矩阵;1是单位列向量;⊗代表直积。
为了方便在容积准则下求解容积点并提高精度,采用文献[11]提出的高阶数值近似方法求解,其中:
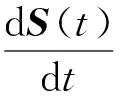
(9)
(10)
式中:Bi,j是Φ(B(t))的第i行、第j列的元素。式(10)可在Matlab里使用ode45命令直接求解,其精度符合要求。
由容积准则,矩阵B(t)可表示为:
B(t)=S-1(t)[X(t)WFT(X(t))+
F(X(t))XT(t)+Q(t)]S-T(t)
(11)
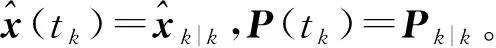
协方差分解:
P(tk)=S(tk)ST(tk)
(12)
计算状态容积点:
(13)
状态容积点传播:
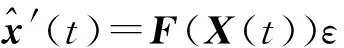
S′(t)=S(t)Φ(B(t))
(14)
(15)
求解预测平方根协方差:
S(tk+1)=[S1(tk+1)S2(tk+1) …S2n(tk+1)]
(16)
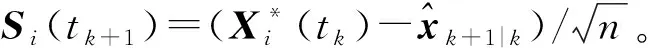
1.2.2 量测更新
测量过程是离散时间的,时间点k是时间t的离散形式。首先计算状态容积点:
Sk+1|k=S(tk+1)
(17)
(18)
容积点的测量传播:
Zi,k+1|k=h(Xi,k+1|k,k+1)
(19)
计算量测预测值:
(20)
构建测量加权中心矩阵:
(21)
计算新息协方差矩阵:
(22)
构建状态加权中心矩阵:
Xk+1|k=
(23)
计算交叉协方差矩阵:
(24)
连续-离散的容积增益为:
(25)
计算状态估计值:
(26)
更新协方差矩阵:
(27)
2 基于M估计的自适应鲁棒平方根连续-离散CKF算法
考虑滤波过程中可能出现的异常因素会导致测量异常,进而影响滤波性能甚至滤波发散,利用校正因子根据观测残差自适应地调整观测噪声协方差矩阵的大小,在测量异常时建立鲁棒机制,从而保证滤波的精确性。
2.1 校正因子设计
由观测残差建立无量纲数Гk+1:
(28)
式中:Rk+1为观测误差协方差矩阵;δ是一个比较小的正实数,本文取0.01。
校正因子ψk+1可如此设计:
(29)
式中:β由经验值取为1.345。
2.2 异常测量判别门限
实际环境带来的测量异常受到多方面因素的影响,测量残差只能从一定程度上对滤波进行修正。在目标的实际状态发生突变时,测量残差也会增大。因此,利用残差和对应的协方差来判断异常测量,将会更好地提升滤波效果。引入标准化新息:
(30)
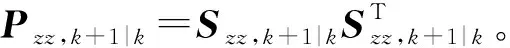
(31)
式中:λk+1表示实测值与预测值的Mahalanobis距离,通过引入新息协方差来衡量统计特性。不妨令标准化新息τk+1服从高斯分布,那么Mahalanobis距离服从卡方分布:
λk+1~χ2(1)
(32)
设卡方分布的置信水平为α,则:
p(λk+1>γα)=1-α
(33)
式中:γα为置信水平α的分位点。
当出现异常测量时,λk+1将不再满足卡方分布。所以只要选择合适的置信水平,确定相应的分位点的值,就可以区分正常测量和异常测量。将以上的判别方法与校正因子相结合,重新定义校正因子μk+1:
(34)
2.3 鲁棒平方根连续-离散CKF算法
基于以上内容,形成了一种具有鲁棒机制的平方根连续-离散CKF方法。其时间更新过程与平方根连续-离散CKF方法一致,在测量更新中,式(18)~(24)步骤不变,而后新息协方差矩阵被重新定义:
(35)
相应的连续-离散容积增益为:
(36)
状态估计值为:
(37)
更新协方差矩阵为:
(38)
可知,通过Mahalanobis距离对异常测量进行门限判别,引入校正因子自适应地调整观测噪声协方差阵的大小,基于连续-离散方法跟踪目标实际运动。该算法在时间更新上使用连续时间状态估计思想,在测量更新上嵌入了异常测量判别和修正方案。根据以上分析,具体的算法流程图见图1。
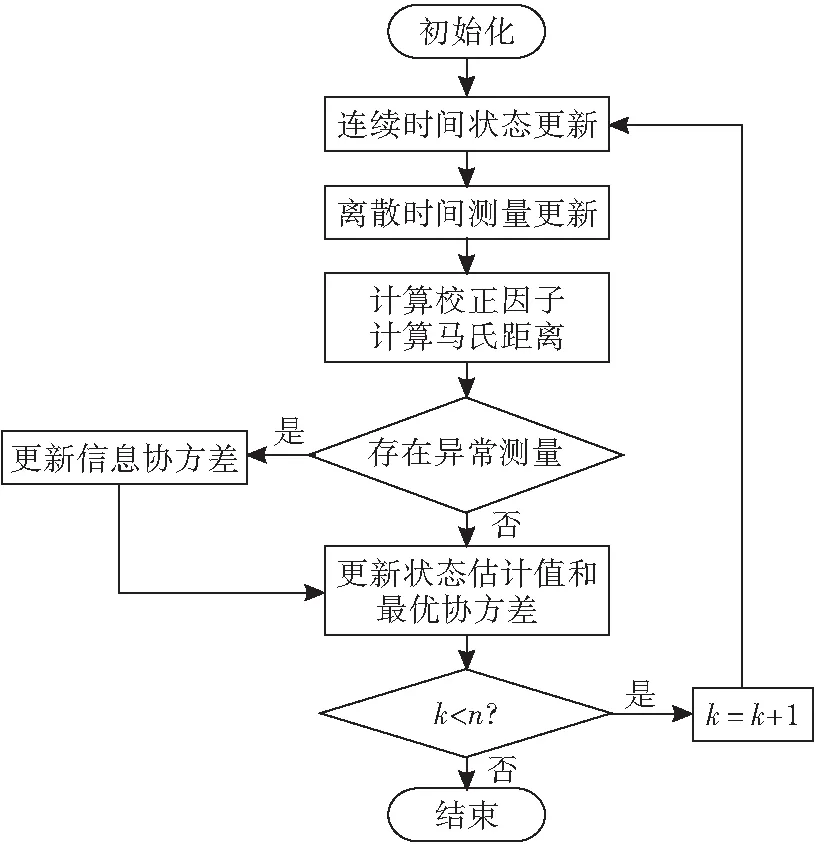
图1 基于M估计的自适应鲁棒平方根连续-离散CKF算法流程图
3 仿真与分析
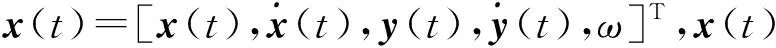
离散时间的非线性测量模型为:
zk=[tan-1(y(tk)/x(tk))]+vk
(39)
测量噪声vk满足零均值的高斯分布,即:vk~N(0,Rk)。本次仿真中Rk的初始值为一维常值0.01。
为了评估滤波的性能,定义位置量的均方根误差(root mean square error,RMSE)。它的计算方法是:
(40)
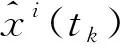
接下来,在测量异常的情况下观察本文提出的算法对目标跟踪的效果。这里分别模拟了单点测量异常和多点测量异常的情况,为了便于区分,分别记作“异常测试1”、“异常测试2”。异常测试1是指在t=150 s时,测量噪声的协方差矩阵变为30Rk。异常测试2的异常测量数据及时间点见表1。
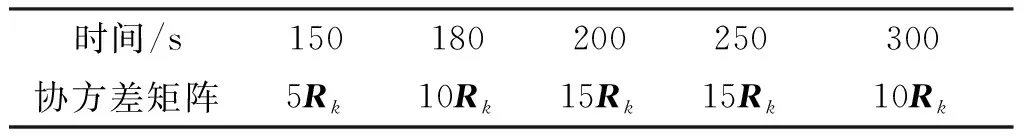
表1 异常测试2测量噪声的协方差矩阵
首先,对本文提出算法的有效性进行验证。在异常测试条件下使用不具有鲁棒性的SRCD-CKF算法进行仿真,鲁棒性测试使用本文提出的MARSRCD-CKF算法。仿真得到的目标轨迹跟踪见图2。
如图2所示,目标的估计轨迹与真实轨迹在测量异常时发生了一定的变化。可以看到,不具备鲁棒性的算法受异常测量的影响较大,估计结果稍差,具备鲁棒性的算法其估计轨迹与真实轨迹更为接近。在两种测试条件下MARSRCD-CKF算法都能够跟踪的更加准确,证明本文提出的鲁棒算法是真实有效的。

图2 转弯运动的轨迹图
为了更清晰地观察异常测试点的误差情况,分析其对滤波性能的影响,做出RMSE随时间的变化曲线见图3。可以看到在各测试条件下滤波都具有良好的收敛性。在t=150 s时,测量异常带来的影响直观表现为RMSE的增加,异常测试2亦是如此。异常测试条件下曲线出现比较陡峭的变化,相应的其再次收敛也比较缓慢;具有鲁棒性的算法受到异常测量影响时变化缓慢,很快重新收敛,且最终估计误差的大小基本与无异常情况下相似。两种鲁棒性能的测试几乎一致,说明不论单个测量点异常,还是多个测量点异常,算法都是有效的。此算法能够解决目标跟踪过程中的异常测量问题。

图3 各测试条件下的RMSE
为进一步评估本文提出的滤波算法的性能,分别在异常测试1和异常测试2下与SRCD-CKF算法和MRSRCD-CKF算法作对比分析,见图4~5。
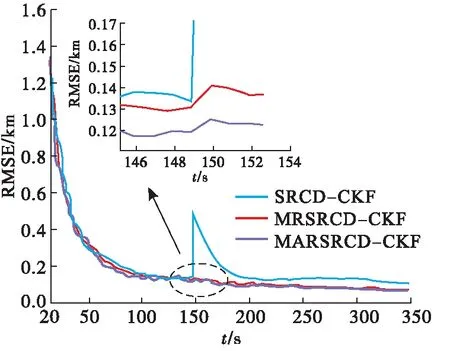
图4 异常测试条件1下的误差对比
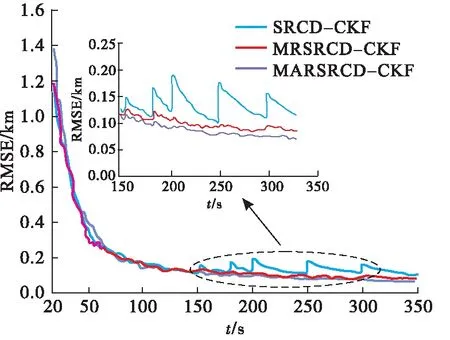
图5 异常测试条件2下的误差对比
如图4所示,各算法在异常测量出现前走势大致相同。在第150 s出现异常测量后,不具备鲁棒性的SRCD-CKF算法误差突然增大,而MRSRCD-CKF算法与MARSRCD-CKF算法都可以抑制异常测量。第150 s之后,MARSRCD-CKF算法比MRSRCD-CKF算法的误差更小,说明本文提出的鲁棒方法在单个测量点异常的条件下比MRSRCD-CKF算法要更有效。
在图5中,在设置的各异常测量点处,不具备鲁棒性的SRCD-CKF算法的估计误差均出现了突然增大的现象,MRSRCD-CKF算法与MARSRCD-CKF算法都有效抑制了异常测量,只有小幅度的波动,并且MARSRCD-CKF算法比MRSRCD-CKF算法的误差更小,说明本文提出的鲁棒方法在多个测量点异常的条件下比MRSRCD-CKF算法要更有效。
4 结语
为了能够应对测量中出现的异常情况,本文提出了一种基于M估计的自适应鲁棒平方根连续-离散CKF算法。假设在一处或者多处测量点处出现异常测量,通过观测残差自适应地调整观测噪声协方差矩阵的大小,建立了相应的校正因子,而后以Mahalanobis距离作为判别门限,对新息协方差矩阵进行更新,进而与连续-离散容积卡尔曼滤波结合形成了MARCD-CKF算法。为进一步提升滤波的精度以及保证协方差矩阵的正定性,本文采用了连续-离散容积卡尔曼滤波的平方根(SRCD-CKF)形式。仿真表明,该算法能够有效限制异常测量的影响,并且比传统鲁棒算法更有效,在目标跟踪系统中优势更为明显。
