响应变量缺失下变系数模型的分位数回归
2022-04-08袁德美
叶 瑶, 袁德美
(重庆工商大学 数学与统计学院, 重庆 400067)
0 引 言
变系数模型最早由Hastie等[1]提出,是重要的非参数模型,可以看作是非参数模型和半参数模型的推广,该模型具有稳健性,且模型假设少,具有更强的适应性。它能很好地分析回归系数随着时间等诸因素的变化。假设Y为响应变量,X=(X1,X2,…,Xp)T∈Rp为p维协变量,则变系数模型有如下形式:
Y=XTβ(U)+ε
(1)
其中,U为光滑变量,β(·)=(β1(·),β2(·),…,βp(·))T∈Rp为未知的关于U的函数向量,模型误差ε与(X,U)相互独立。
在统计工作中,由于调查人员的疏忽,需要的信息暂时还没办法获得,获取成本很高,因此难免会遇到缺失数据。Rubin对缺失机制的问题构造了3种概念:完全随机缺失(MCAR)指是数据的缺失与完全观测数据和不完全观测数据都无关;随机缺失(MAR)是数据缺失与完全观测数据有关,与不完全观测数据无关;不完全缺失(MNAR)是指缺失数据与不完全观测数据本身有关。近几十年,对于缺失数据下变系数模型的研究也有很大的进展。李志强等[2]采用最小二乘方法,分别用拟似然借补估计和加权拟似然借补估计来处理缺失数据,发现两种方法估计的精度差别不大;Cai等[3]用局部多项式估计方法估计系数函数,并推导出系数函数的标准误差公式,提出一种基于非参数最大似然比的拟合优度检验技术。这些研究都是基于最小二乘方法展开的,最小二乘方法计算简单,但前提条件比较苛刻,对离群点敏感。为了提高估计的效率,Koenker等[4]提出了分位数回归模型,它是根据被解释变量的条件分位数对解释变量进行回归,不需要对误差项的分布作假设,适应性更强;Honda[5]将系数函数用局部多项式方法展开,研究了变系数分位数回归模型的参数估计问题,证明了其渐进性质;Guo等[6]用局部复合分位数方法研究了误差项带有异方差的变系数模型,提出的新方法可以对系数函数和异方差同时进行估计。

为未知参数向量。
除了用局部多项式近似未知的系数函数,还可以用样条估计方法近似逼近系数函数。1946年,Schoenberg提出了B样条估计方法,Zhao等[10]用B样条方法逼近半参数变系数部分线性模型的系数函数部分,结合SCAD惩罚方法,研究了模型的变量选择问题;Du等[11]研究了B样条近似的变系数部分线性模型的变量选择,与Zhao等[10]不同的是他们选择了分位数回归方法,在选择重要变量的同时又估计了未知系数;Jin等[12]将B样条和逆概率加权相结合,考虑了当协变量缺失时,变系数部分线性模型的复合分位数回归,并结合了自适应Lasso方法,研究了变量选择问题。
相较于均值回归模型,分位数回归模型不仅可以避免均值回归因异常值或极端值对于统计推断的影响,而且挖掘出的信息更加丰富,获取的数据对响应变量的描述更完整。对于缺失数据下的变系数模型,使用局部多项式近似系数函数的研究已经有很多,但该方法存在以下问题:第一,计算速度比较慢;第二,涉及窗宽的选择,且对窗宽很敏感;第三,涉及拟合多项式阶数的选取。所以这里选择B样条近似逼近系数函数。B样条可以将式(1)转换为样条基的线性组合,操作起来方便,且只需要简单节点数的选择,对节点数目不太敏感。对于基于B样条的回归问题,鲜有学者将其与缺失数据结合起来,而缺失数据在统计工作中难免会遇到。因此,本文针对响应变量随机缺失,研究了变系数分位数回归模型的参数估计问题。首先用logistic模型产生响应变量的缺失概率,然后对变系数模型的系数函数采用B样条逼近技术,利用缺失概率构建逆概率加权分位数回归损失函数,得到模型的未知系数函数估计,通过模拟研究证明所研究方法的有效性,最后通过实例分析进一步证明方法的合理性。
1 变系数分位数回归的IPW估计

(2)
其中,β(·)=(β1(·),β2(·),…,βp(·))T∈Rp为系数函数;Xi∈Rp,Ui∈R,(Xi,Ui)可以完全观测到;Yi随机缺失,当δi=1时,Yi可以观测到;当δi=0时,Yi缺失。大多数的文献中都假定缺失机制是随机缺失的,同时这也符合普遍的实际情况。这里假设Yi是随机缺失的,则有以下关系:
P(δ=1|X,U,Y)=P(δ=1|X,U)
其中,γj=(γj1,γj2,…,γjKj)Τ,j=1,2,…,p。
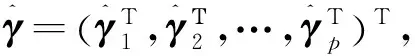
(3)

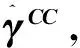
(4)

在实际情况中,缺失概率一般来说是未知的,缺失概率在很多文献中也被称为倾向得分。对于缺失概率的估计,许多学者选择用非参数估计,比较常用的非参数估计是Nadaraya-Watson估计,形式如下:
其中,Kh(·)=K(·/h)/h是带宽为h的核函数,维数为p,(Ui,δi),i=1,2,…,n,为来自(U,δ)的一个随机样本。显然,这种非参数估计在U为高维的情况下可能出现“维数灾祸”的问题,因此本文考虑使用参数估计方法来估计缺失概率。假设
P(δ=1|X,U,Y)=P(δ=1|X,U)=
P(δ=1|Zi)=π(Zi,α)
(5)
其中Zi=(Xi,Ui)T,假设
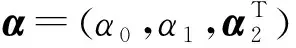


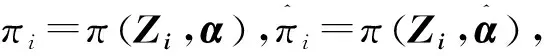
(6)
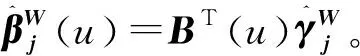
节点数目在未知系数函数的光滑程度和将拟合的数据之间起到一个平衡的作用。对于节点数kn的选择,可以极小化某个准则函数来实现,常用的准则函数有AIC信息准则、BIC信息准则、交叉验证和广义交叉验证。He等[18]发现,在选择B样条的节点数时,用信息准则选取要优于用交叉验证和广义交叉验证,而AIC信息准则容易出现过拟合的现象,即节点数目选得过大。所以选择极小化BIC准则来选择节点数目:
(7)

2 数值模拟
2.1 计算过程



其中,i=1,…,2M+kn-q。上述公式为Cox-de-Boor递推公式。根据递推公式产生3次B样条基函数,然后根据式(7)的BIC准则实现节点数的选择;
2.2 模拟准备
考虑模型:
Y=β1(U)X1+β2(U)X2+0.5ε
其中,X1~N(0,1),X2~N(0,1),U~U(0,1),ε~N(0,1),系数函数β1(u)=cos 2πu,β2(u)=sin 2πu,假设X1,X2,U,ε相互独立。
用logistic模型产生缺失数据,考虑如下两种缺失机制:
随机生成n个服从二项分布的δ,生成的概率为上述两种缺失概率,根据程序模拟出的两种缺失概率的比例约为11%和33%。
对于τ=0.25,0.5,0.75,抽取的样本容量为n=100,200时,分别模拟300次,取300次模拟结果的平均值作为最终的估计值,计算β的以下3种估计:

其中,ngrid为估计β(u)时格子点的数量。
2.3 模拟结果与结论
根据以上模拟前的准备,按照计算过程中的思路,用R软件模拟得到如下结果(表1,表2,图1,图2):
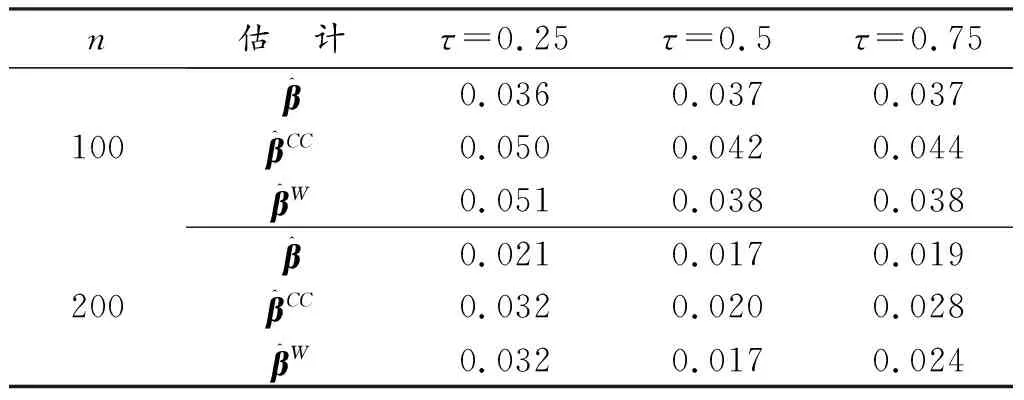
表2 β(U)3种估计的RASE值(缺失概率2)


图1 3个分位点IPW估计拟合效果(缺失概率1)
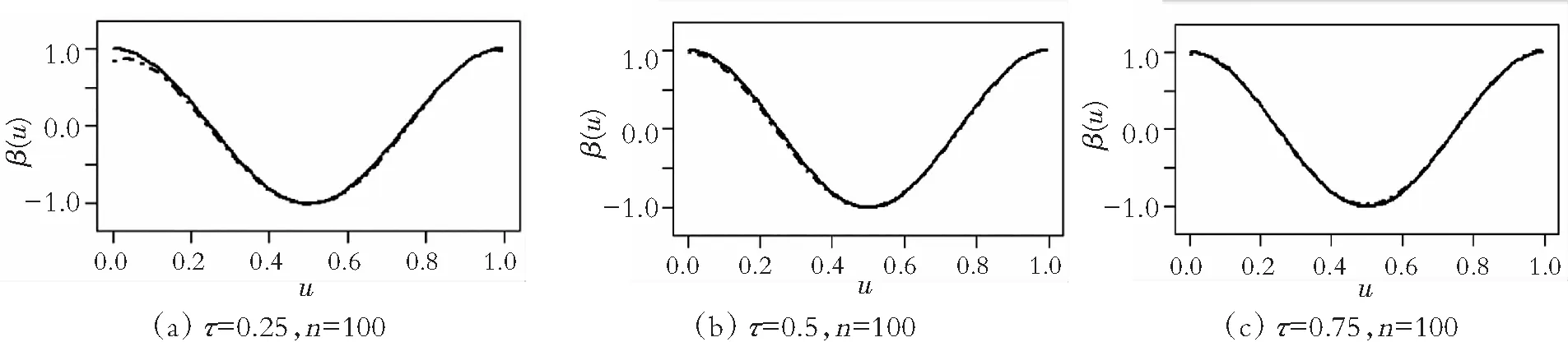
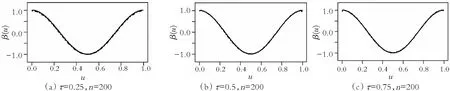
图2 三个分位点IPW估计拟合效果(缺失概率2)
图1,图2黑色实线代表真实曲线,虚线代表拟合曲线。其中,从左到右依次代表τ=0.25,0.5,0.75时,β1(U)的逆概率加权估计拟合曲线。从上到下依次代表n=100,200时的逆概率加权估计拟合曲线。
表1和表2分别展示了两种缺失机制下β的3种估计的平均均方差平方根值,从模拟结果可以得到以下结果:
(1) 利用完全数据分位数回归估计,结果整体上比相应的基于逆概率加权的分位数回归方法的RASE值偏大,说明基于逆概率加权的分位数回归较基于完全数据的分位数回归估计效果好;
(2) 对于同一个估计,随着样本量的增加,对应的模拟结果数值也会减小,说明样本量的增加也会减小3种估计的平均均方差;
(3) 对比两种缺失机制,第二种缺失机制的RASE值普遍大于第一种缺失机制的RASE值,说明缺失比例越高,估计效果越差。
图1和图2展示了当n=100,200时,3个分位点下分别模拟300次β1(U)的IPW估计拟合效果图。从图中也可以看出,样本量越大,拟合效果越好,且缺失比例越大,拟合效果越差。总之,在响应变量随机缺失下,将B样条和逆概率加权相结合的变系数模型分位数回归在有限样本情况下表现良好。
3 实例分析
接下来用本文所研究的利用B样条结合逆概率加权的方法研究空气污染的数据集。二氧化氮是形成光化学烟雾和酸雨的主要物质之一,它会直接攻击人体的肺部,对人体造成很大的危害,尤其是老人或者呼吸系统有疾病的人,当二氧化氮的累计浓度增大时,会与大气中的臭氧发生化学反应,造成臭氧的损耗,而臭氧就像一把保护伞可以保护我们免受短波紫外线的伤害,所以研究二氧化氮浓度与哪些因素有关很有必要。许多学者拿该组数据研究变系数模型,比如Tang和Sun 等[8-9]。
该组数据来源于StatLib,是由挪威公共道路管理局收集的关于挪威奥斯陆地区的相关数据,时间跨度为2001-10—2003-08,目的是研究空气污染与道路车流量和气象因子之间的关系。该数据集的样本量为500个,其中包括的变量有每小时二氧化氮(NO2)浓度的对数(粒子)、每小时车流量的对数、离地面2 m的温度(℃)、风速(m/s)、离地面25 m与离地面2 m的温度差(℃)、风向(0°~360°之间)、每天的时刻、从2001年10月1日到观测时间隔的天数。
参照Sun等[9],设响应变量Y为每小时的对数二氧化氮浓度,协变量x1为每小时对数车流量,x2为风速,t为每天的时刻,利用本文提出的方法研究Y与x1,x2以及t之间的关系,建立以下模型:
Y=β1(T)X1+β2(T)X2+ε
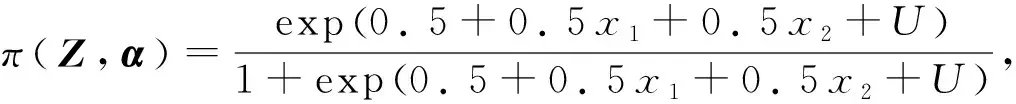
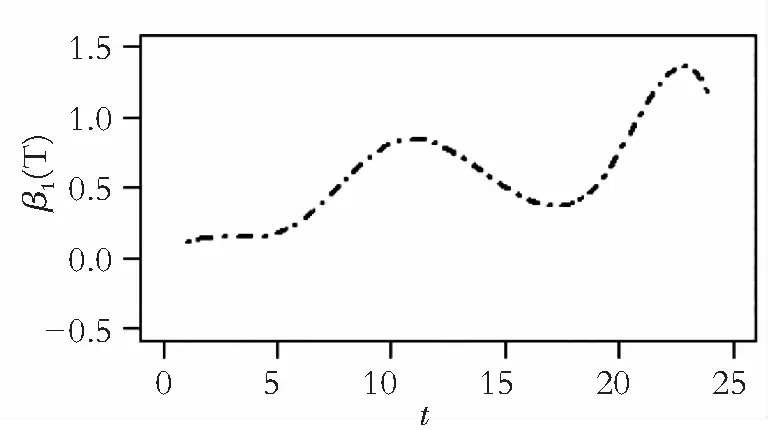

图3 系数函数β1(T)和β2(T)估计
从图中可以看出,二氧化氮浓度与每小时的对数车流量成正相关,说明每小时经过的车辆越多,二氧化氮浓度越高;风速对二氧化氮浓度的影响为负,即在其他条件不变时,风速越大,二氧化氮浓度越低,这与实际情况是一致的;化石燃料的燃烧会带来大量的二氧化氮,所以车流量越大污染越严重;当风速大时,大气流动性越强,二氧化氮进入大气后会被稀释,浓度就会降低。
近几年,环境保护已经成为热点讨论话题,针对实例分析结果,提出以下几个建议:从根源上减少汽车尾气排放,在技术上,可以对汽车尾气处理技术做出改进,对尾气处理技术不达标的汽车进行淘汰或者改造,对汽车的发动机做出改进,使得燃烧更充分等;对城市的交通规划做出改进,尤其是在上下班高峰时,避免因道路拥挤造成发动机燃油燃烧不充分,燃油燃烧不充分时排放的二氧化氮是正常行驶情况下的好几倍,合理的交通规划可以缓解城市拥堵的现象;从民众层面上讲,政府要主动积极宣传生态环保、绿色出行理念,增强居民环境保护意识和综合素质,大力推进新能源汽车的使用,鼓励市民使用公交、地铁出行;发动群众力量植树造林,尽可能减小汽车尾气带来的危害。同时,还需要立法执法,比如严格要求汽车的排放标准以及燃油标准,限制排量大的汽车的出行时间和区域;杜绝任何人或者组织实施任何破坏环境的活动,做到有法可依,执法必严。
4 结束语
本文研究了变系数模型,用B样条技术逼近变系数模型的系数函数,基于逆概率加权,构造了响应变量缺失下分位数回归估计的损失函数,得到了未知系数函数的估计。在模拟研究中,用没有数据缺失时的系数函数估计作为参考,与直接使用完全数据的估计方法进行对比,模拟研究证明了该方法的有效性。将该方法应用到挪威公共道路管理局收集的关于奥斯陆地区的相关数据中,研究了空气中二氧化氮浓度与道路车流量和风速之间的关系,发现二氧化氮浓度与每小时的对数车流量成正相关,与风速成负相关关系,与实际情况一致,进一步证明了所研究方法的合理性,并给出了部分建议。
本文考虑的模型是变系数模型,还可以将模型推广到部分线性变系数模型、单指标变系数模型等;对于缺失数据问题,除了本文研究的响应变量缺失,还可以考虑协变量缺失或者响应和协变量同时缺失时的情形;对于B样条逼近技术中节点数的选择,假设每个系数函数估计所需要的节点数是相同的,还可以考虑节点数不同的情况。这些问题都是后续研究的重要内容。
