基于VMD-LSTM的触电电流提取方法研究

李春兰 王静 石砦 王长云 罗杰 任鹏

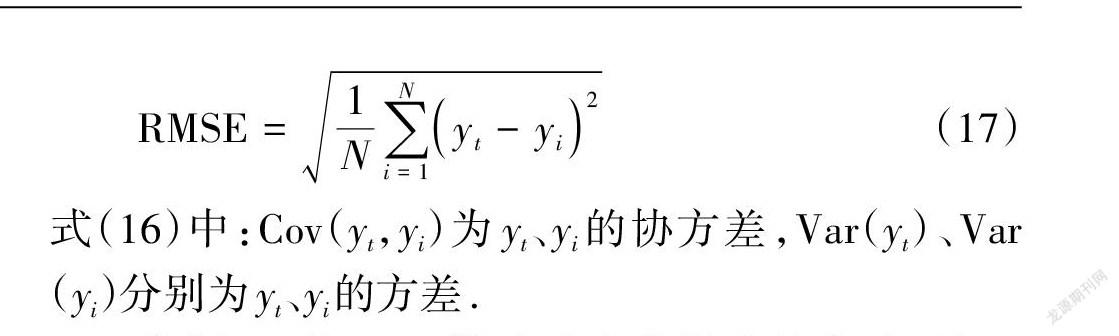
摘要：为有效提取触电故障特征，实现从剩余电流中分离出触电电流，提出了一种基于变分模态分解（Variational Mode Decomposition，VMD）与长短期记忆神经网络（Long Short Term Memory，LSTM）相结合的触电电流提取方法.利用果蝇优化算法对VMD参数[K，α]寻优获得最优参数组合[6，280]，以VMD分解的剩余电流最佳模态分量突变特性为依据，定义相邻周期电流幅值和的增长率η1、η2作为判别触电事故的特征量;以6层模态分量信号重构触电信号，构建基于LSTM网络的触电电流检测模型.240组触电信号研究结果表明：当η1、η2至少一个满足大于1%时，均发生触电，否则无触电事故发生;相比于VMD-BP、VMD-RBF检测模型，VMD-LSTM检测模型提取的触电电流与真实触电电流的相关系数平均值分别提高了6.2%、2.3%，均方根误差平均值分别降低了36.8%、27.1%，提出的方法具有更高的检测精度.研究结果为研发基于生物体触电电流动作的剩余电流保护装置提供了参考.

关键词：剩余电流;VMD;LSTM网络;触电故障检测;信号提取

中图分类号：TM774

文献标志码：A

剩余电流保护装置作為广泛应用于低压电网中的安全设备，在实际应用中存在拒动、误动等现象[1].为减小或消除剩余电流保护装置动作死区，提高其动作可靠性，需研发基于生物体触电电流动作的剩余电流保护装置.目前亟需解决的问题是触电故障时段的检查及从剩余电流中提取触电电流.

国内外学者在触电电流检测方面做了诸多研究，李春兰等[2]利用小波变换和BP神经网络、关海鸥[3]等利用数字滤波和径向基神经网络均建立了从剩余电流中提取触电电流的神经网络模型，但都存在神经网络易陷入局部最优、训练结果不稳定等问题.韩晓慧等[4]提出滤波技术结合最小二乘支持向量机优化方法建立触电电流检测模型，检测误差小于径向基神经网络模型，但该方法需要大量触电信号进行关系训练，且对触电信号非峰值预测准确性低于峰值预测结果.基于此，刘永梅等[5]提出利用神经网络对触电信号非峰值拟合、对峰值利用支持向量机拟合的触电电流检测方法，提升了触电信号检测的准确性，但存在峰值范围阈值选取过程繁杂的问题.王金丽等应用Hilbert-Huang变换提取模态分量多维度能量特征向量，通过模糊遗传神经网络识别触电类型，存在无法判别触电时段的问题.高阁等[7]采用经验模态分解（Empirical Mode Decomposi⁃tion，EMD）及其改进算法对触电信号分析，提出利用第一层模态分量中的突变点判断触电时刻，但该方法对电源电压过零点时刻触电的识别失效.

Dragomiretskiy[8]根据维纳滤波和变分问题提出了变分模态分解（Variational Mode Decomposition，VMD），采用非递归分解方式通过构造并分解约束变分问题来实现对信号的分解，抑制了模态混叠现象，适用于多领域信号预处理研究[9-11].长短期记忆神经网络（Long Short Term Memory，LSTM）是一种时间循环神经网络，避免了传统循环神经网络产生的梯度消失与梯度爆炸问题，能综合学习长期依赖关系，大量提取数据深层特征，被广泛应用于时间序列数据的处理[12-14].

鉴于此，本文提出了一种基于VMD-LSTM的触电电流检测模型，其目的是通过变分模态分解获得触电故障特征，进一步搜寻触电时段;再将重构后的触电信号结合长短期记忆神经网络构建触电电流识别模型，提取触电电流，为研发基于生物体触电电流动作的剩余电流保护装置奠定基础.

1变分模态分解优化算法

1.1变分模态分解原理

VMD是一种自适应信号处理方法，可将非平稳信号f分解为K个模态分量子信号uk，且每个分量有一个确定的有限带宽和中心频率ωk.约束条件的变分问题为：

式中：{uk}={u1，...，uK}、{ωk}={ω1，...，ωK}分别为所有模态及其中心频率，∂t为对t求偏导数，δ（t）为狄拉克分布，*表示卷积.为了求解式（1），可引入二次惩罚因子α和拉格朗日乘法算子λ将式（1）转换为非约束变分问题，增广拉格朗日函数表示如式（2）：

和λ求解式（2）的最优解，其求解迭代过程见文献[8]，由此可得：

式中：f̂（ω）、ûn（ω）、λ̂n（ω）和ûn+1（ω）分别表示f（t）、un（t）、λn（t）和un+1（t）的傅里叶变换;τ为更新参数，nlk为迭代次数.

∑迭代的收敛条件如式（6）所示：

式中：ε1为预设定的收敛误差.

1.2基于FOA优化的VMD算法

利用VMD进行信号处理时，分解结果受IMF个数K和二次惩罚因子α的影响[15].K值过大或过小会产生虚假分量或丢失分量;α越大或越小会使分解后的各IMF分量的带宽偏小或偏大，因此需优化参数K和α.果蝇优化算法（Fruit FlyOptimization Algorithm，FOA）是Pan提出的一种全局优化智能算法[16].FOA算法所需调整的参数少，克服了遗传算法GA、粒子群算法PSO、蚁群算法等相似的群体智能算法执行时间长的缺点，具有全局搜索能力强并且运算精度高的优点.本文利用FOA算法对VMD参数组合[K，α]同时寻优.考虑熵不但能反映概率分布的均匀特性，还能评价信号的稀疏特性，包含大量故障特征的IMF分量，稀疏性较强，包络熵较小[17].因此考虑将包络熵的最小值作为适应度函数，以此搜寻最优参数组合[K，α]，包络熵适应度函数为：

式（7）中，i=1，2，...，N，N为信号采样点数;Ee为包络熵;信号f（t）经Hilbert变换后的包络信号为a（i），a（i）的归一化结果为ei.

FOA-VMD算法实现步骤为：

1）初始化{û1k}、{ω1k}、λ̂1、n、VMD最大迭代次数m，以及种群规模sizepop、FOA最大迭代次数m、果蝇初始位置X。、Yo;

2）参考文献[16]提供的F0A算法步骤，获得最

优参数组合[K，a];

3）根据式（3）至式（5）计算g+（ωω+1、入+（w）;

4）满足式（6）收敛条件或≥m1，停止迭代，信号f（t）被分解为K个模态分量;否则n=n+1，返回步骤3）.

2基于最佳分量幅值和增长率的触电时段判定

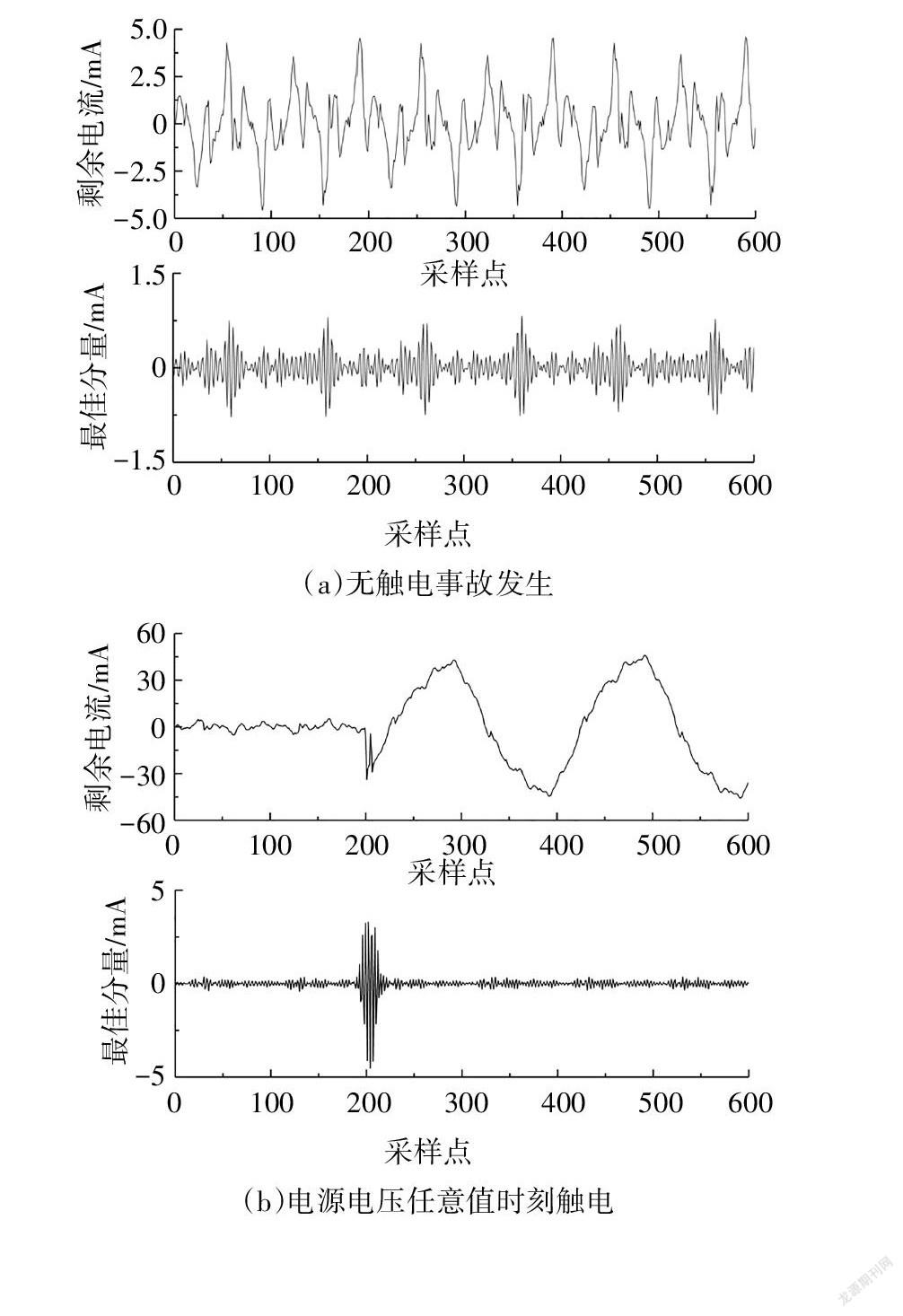
从剩余电流分量中提取触电电流前，需进行触电事故判定.考虑触电信号属于弱信号[18]，且不同触电时刻的触电故障现象存在差异，通过剩余电流信号无法直观确定触电故障时段，而峭度是一个适用于故障诊断的无量纲参数，故障特征越明显的最佳模态分量，峭度越大[19].鉴于此，本文提出以剩余电流变分模态分解的最佳分量为对象，进行触电故障时段检测.图1为不同触电时刻剩余电流信号及其变分模态分解最佳分量.

分析图1可知，在触电时刻最佳分量发生突变，根据该突变特性提出利用最佳分量相邻周期电流幅值和的增长率判定触电时段.其具体计算步骤为：

1）确定最佳分量.计算各模态分量的峭度，将峭度最大值的模态分量作为触电信号的最佳分量，峭度ku表达式如∑式（8）：

式中：第k个模态分量第i个采样点为u（ki）（i=1，...，N），uˉk为相应模态分量的平均值.

2）最佳分量信号归一化处理，如式（9）：

3）计算最佳分量各周期采样点的电流幅值和S

式中：J为截取触电信号的周期个数，本文取J=3，S

（j）为该信号第j个周期采样点的电流幅值之和（j=1，2，3）.4）本节提出根据最佳分量相邻周期电流幅值和的增长率η1、η2范围确定触电故障时段，如式（11）：

3基于VMD-LSTM的触电电流提取研究

3.1LSTM网络结构

LSTM是循环神经网络（Recurrent Neural Net⁃work，RNN）的一种特殊类型，由Hochreiter等提出，并由Kratzert等[20]改进，避免了RNN存在的梯度消失及爆炸问题.引入记忆单元及门控单元是LSTM结构的核心思想，在隐藏层各神经单元中增加记忆单元使神经网络具备了长期记忆功能，门控单元可以保护和控制神经元细胞状态信息.图2为LSTM的单元结构示意图.

图2中，当前单元输入为xt、ht-1及lt-1，输出为ht、lt.其中ht-1、ht分别为t-1、t时刻的输出，lt-1、lt分别为t-1、t时刻的隐层输出.f、i、o分别为t时刻遗忘门ttt值、输入门值及输出门值，ct代表t时刻的候选记忆;Wf、Wi、Wo、Wc分别为相应的权重矩阵.LSTM各单元计算过程如式（12）：

式中：bf、bi、bo、bc分别为相应的偏置项;Uf、Ui、Uo、Uc分别为对应的回归权重矩阵;σ（·）为Sigmoid激活函数，使输出值在[0，1]，tanh（·）为双曲正切激活函数，使输出值在[-1，1].

按式（12）进行记忆单元信息的读取和修改，可得表达式为：

式（13）中，⊙表示矩阵元素相乘.

3.2基于VMD-LSTM的触电电流提取模型

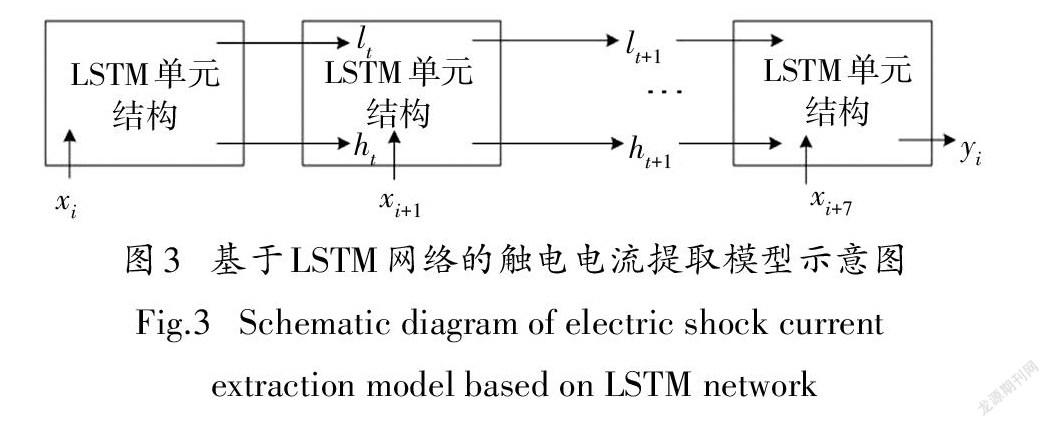
针对触电信号，本文提出利用8个LSTM单元构成触电电流检测模型，如图3所示.其中，x（i=1，i2，···，N-7）为LSTM网络输入，y（ii=1，2，···，N-7）为网络输出，分别由剩余电流和触电电流各VMD模态分量根据式（14）重构获得.

式中：z为重构的触电信号，K为分解层数，uk为模态分量.

基于LSTM网络的触电电流提取模型的损失函数为均方差（Mean Squared Error，MSE），如式（15）：

式中：yt为实际触电电流，yi为预测触电电流，ε2为预设误差.

为证明本文方法的有效性，采用相关系数ρ与均方根误差（Root Mean Square Error，RMSE）评价模型.如式（16）、式（17），预测值与实际值越逼近，ρ值越大，模型预测值越准确，RMSE值越小.

式（16）中：Cov（y，y）为y、y的协方差，Var（y）、Var（y）分别为y、y的方差.依据1.2节VMD算法及本节提出的方法，基于

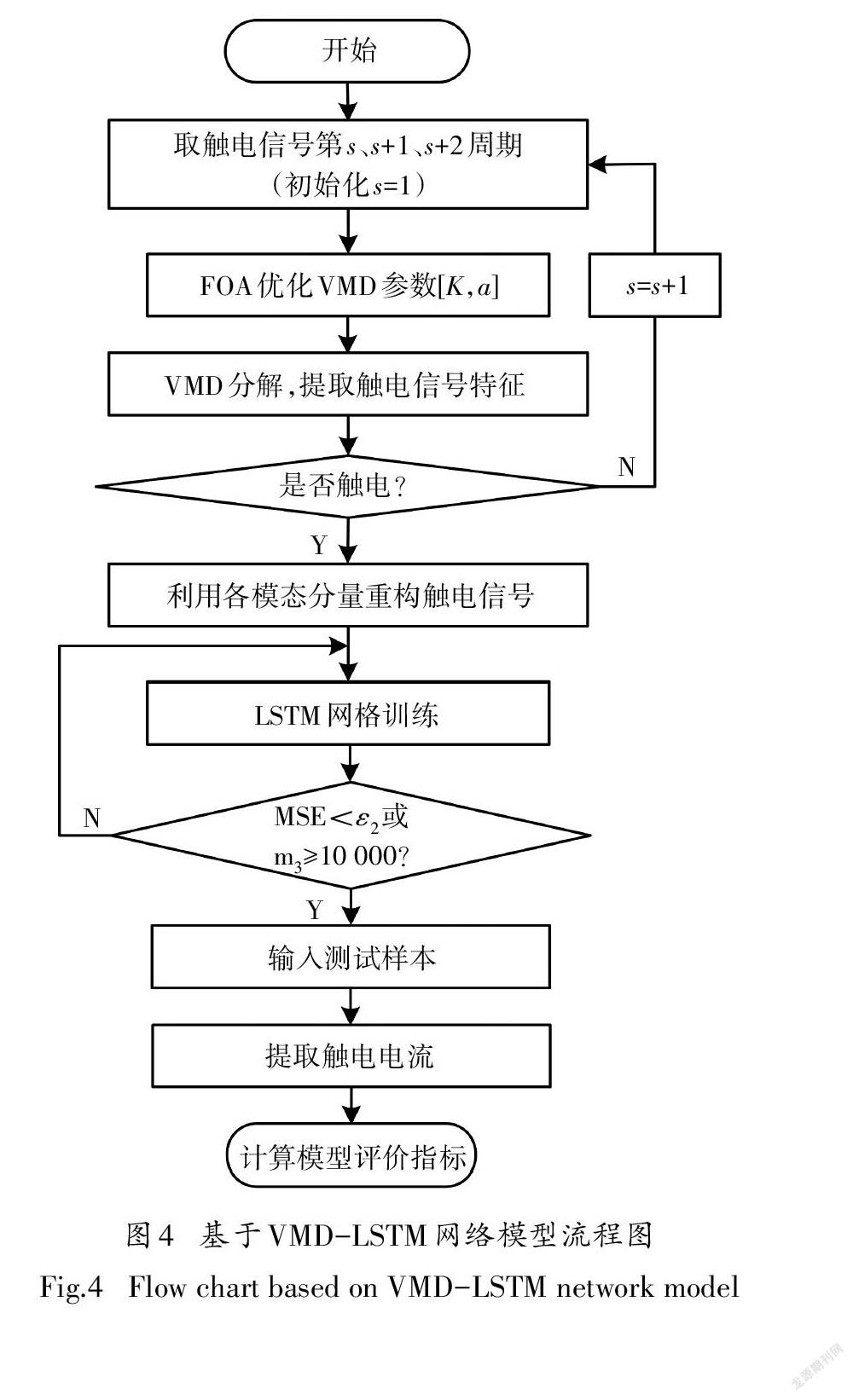
VMD-LSTM网络提取触电电流的步骤为：

1）初始化：{û1k}、{ω1k}、λ̂1、n均为0，m1为500，siz⁃epop为30，m2为100，（X0，Y0）取（1，1），LSTM神经网络学习率为0.001，最大迭代次数m3为10000次，时间窗口大小为8，隐含层节点数为64.

2）根据1.2节FOA-VMD算法步骤，获得剩余电流及触电电流的各模態分量.

3）根据2节提出的触电故障判定步骤提取触电信号特征，判断是否发生触电故障，若发生触电故障，进入步骤4）;否则，更新触电信号并返回步骤2）.4）利用各模态分量重构触电信号，输入到本节图3示意的LSTM触电电流提取模型，获得触电电流.

所提算法的流程如图4所示.

4试验分析

4.1触电试验信号

本文选取的原始触电信号是课题组通过搭建动物触电物理试验平台采集的动物触电信号.试验对象为体重分别为26、32、39kg的三只哈萨克羊与体重分别为14、18、23kg的三只新疆白猪，三相调压器输出电压为（36±0.5）V，频率为50Hz.故障录波器采样频率为10kHz[21].动物触电物理试验平台如图5所示.

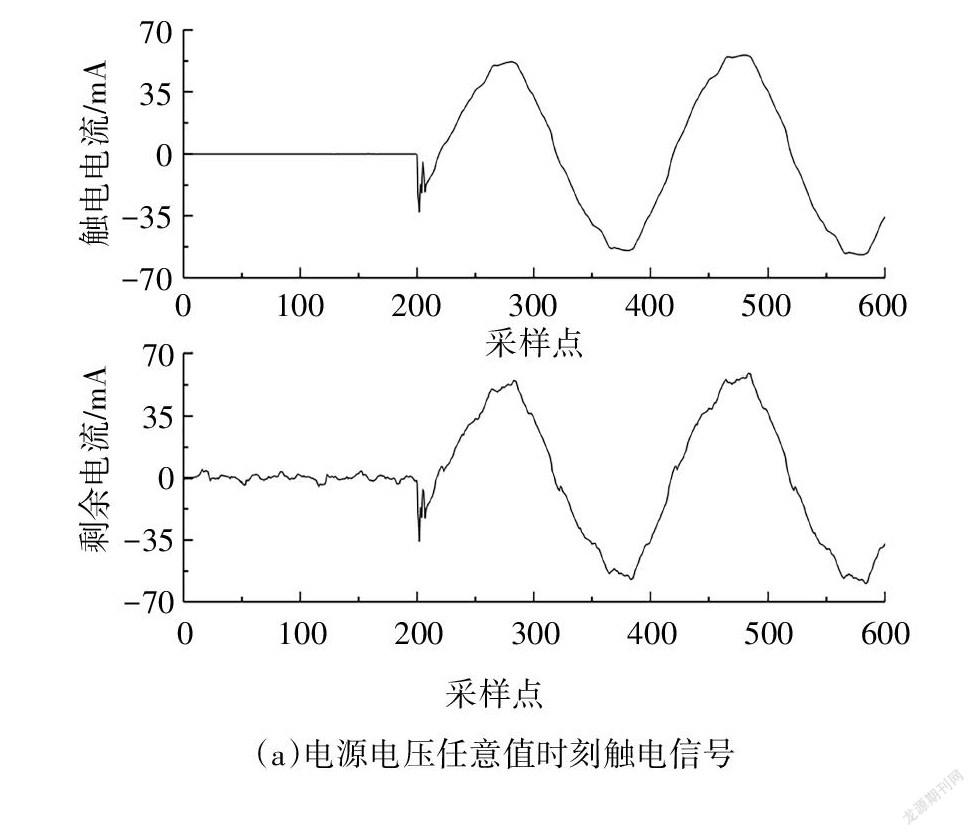
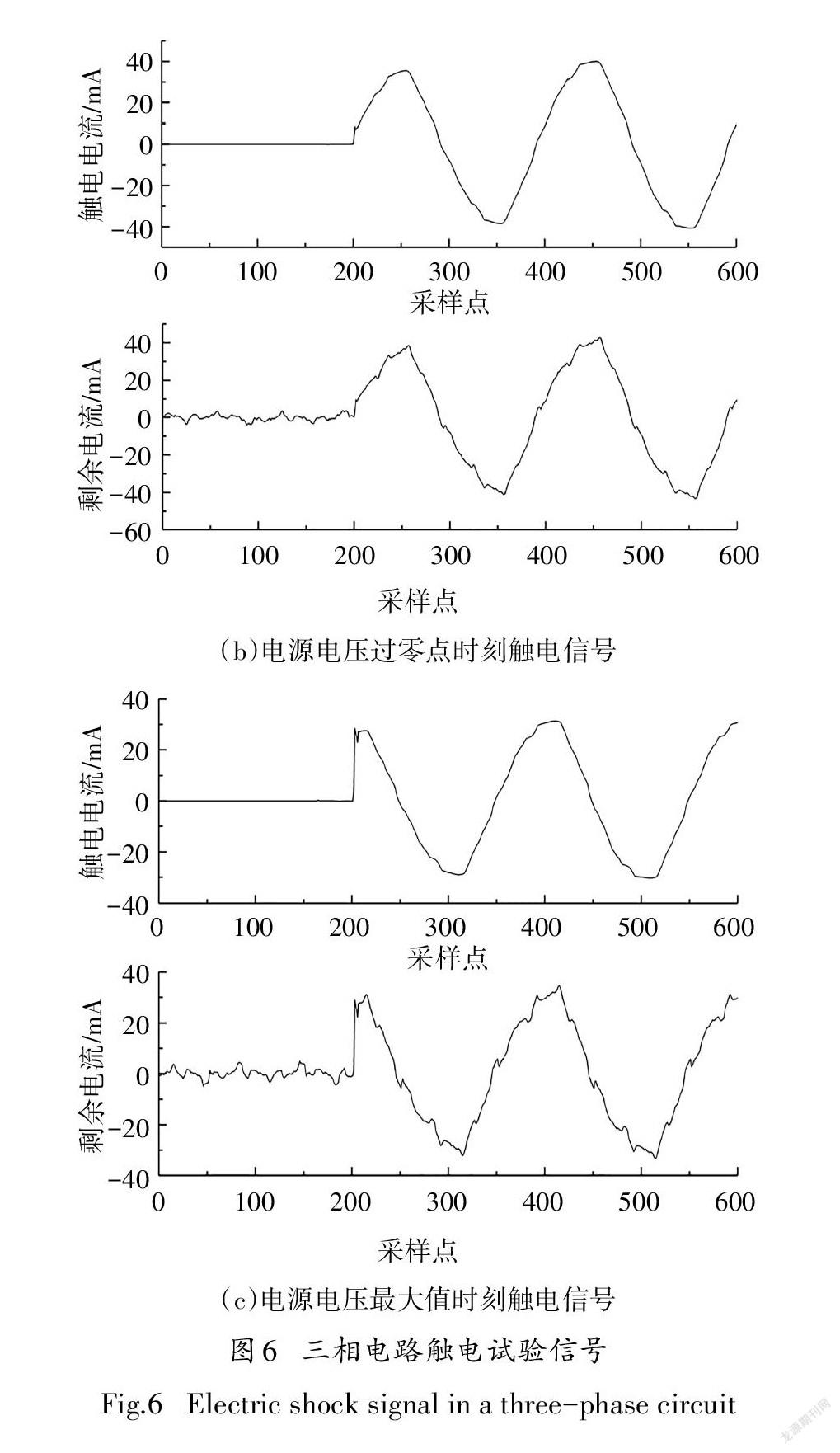
本文共采用240组数据样本，其中200组用于算法的训练，40组用于测试.200组训练样本包括电源电压最大值时刻触电、电源电压过零点时刻触电各60组，电源电压任意值时刻触电样本80组.40组测试样本包括电源电压最大值时刻触电、电源电压过零点时刻触电各10组，电源电压任意值时刻触电样本20组.每组数据分别截取工频3个周期的信号波形，共600个采样点.三相电路时三种典型时刻的剩余电流及对应触电电流如图6所示.

4.2触电事故时段判别

本文选取三种典型时刻触电信号各15组，利用1.2节提出的FOA-VMD算法获得各组信号最优参数组合[K，α]，综合考虑45组结果，本文最佳参数组合取为[6，280].图7所示为某一组信号参数K和α的寻优迭代过程.

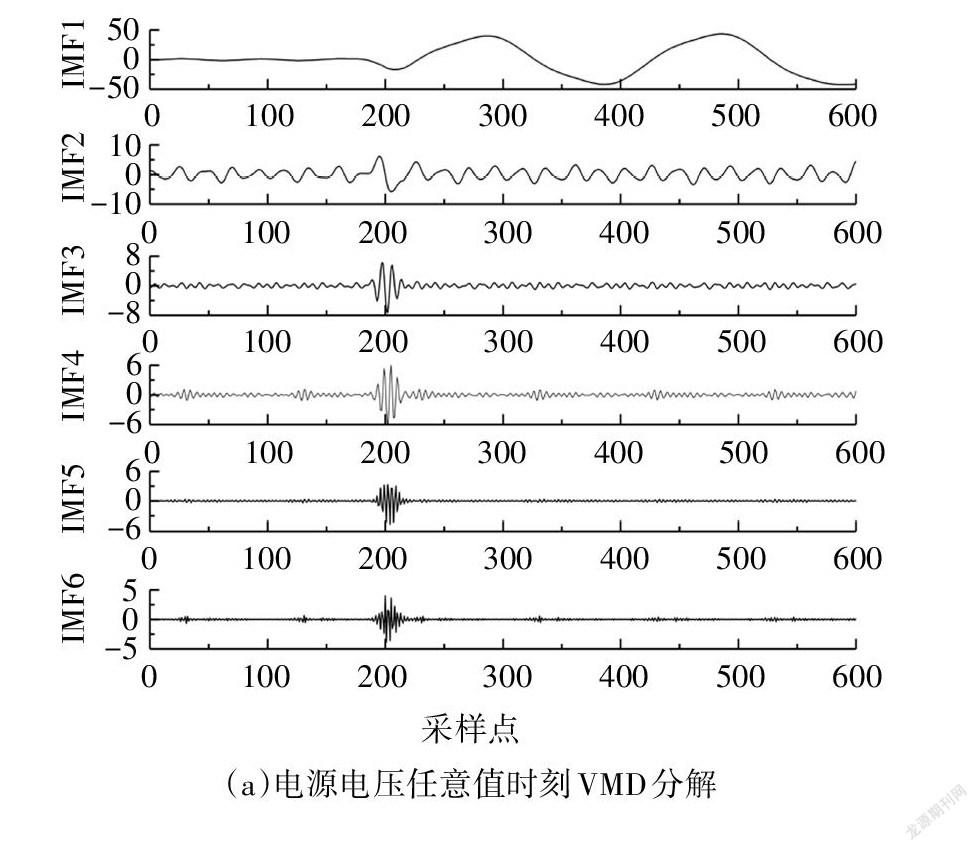
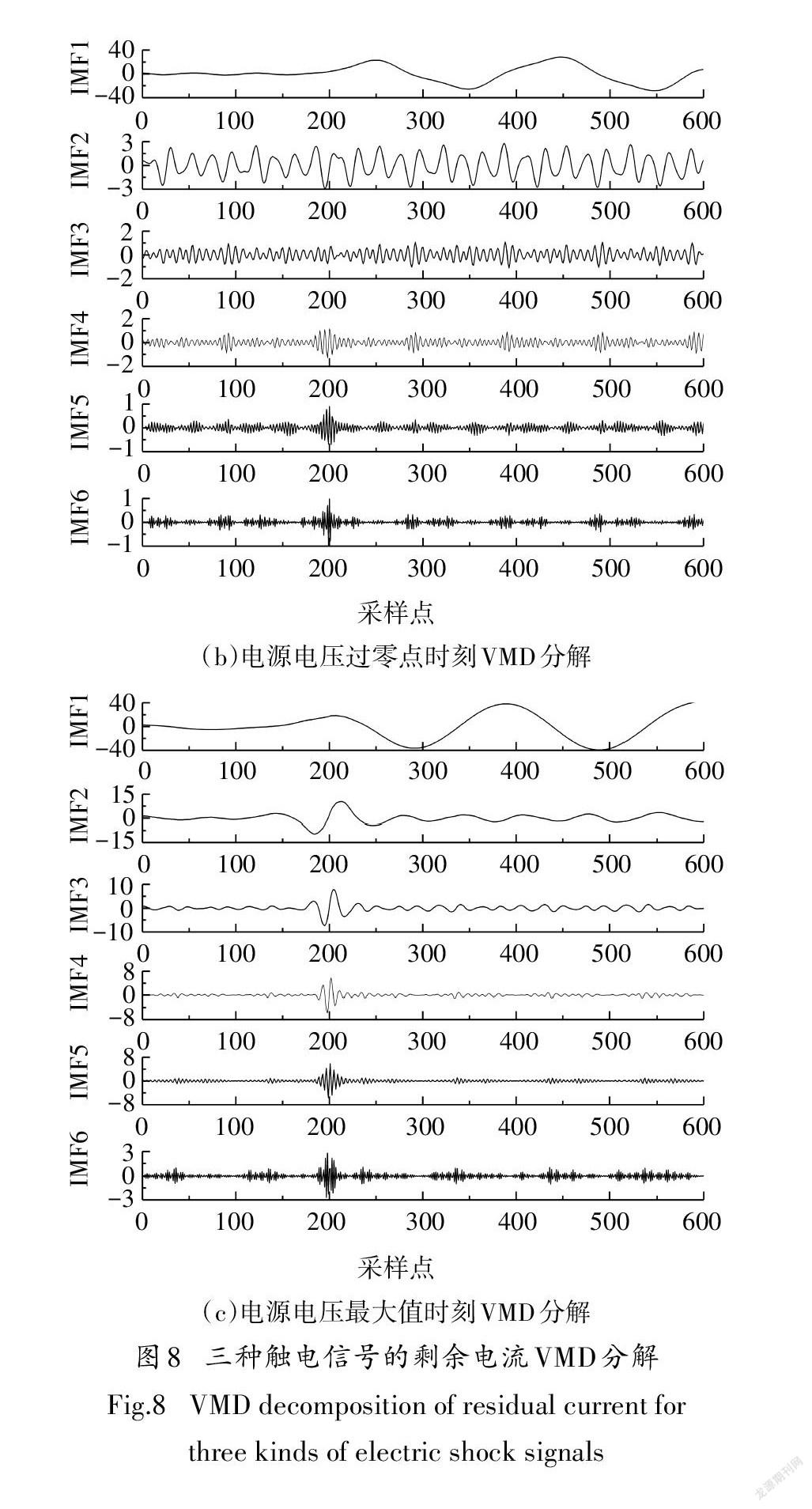
分析图7可知，群体进化到第65代时得到了局部极小熵值3.658，对应最佳参数组合为[6，280].根据最优参数组合[6，280]，图6中三种触电信号的剩余电流VMD分解如图8所示.根据式（8）计算图8各模态分量的峭度，如表1所示.

分析表1可知，三种触电时刻剩余电流信号IMF5分量的峭度值最大，作者对240组触电信号对应模态分量的峭度计算可得到同样的结论，因此IMF5为最佳分量.

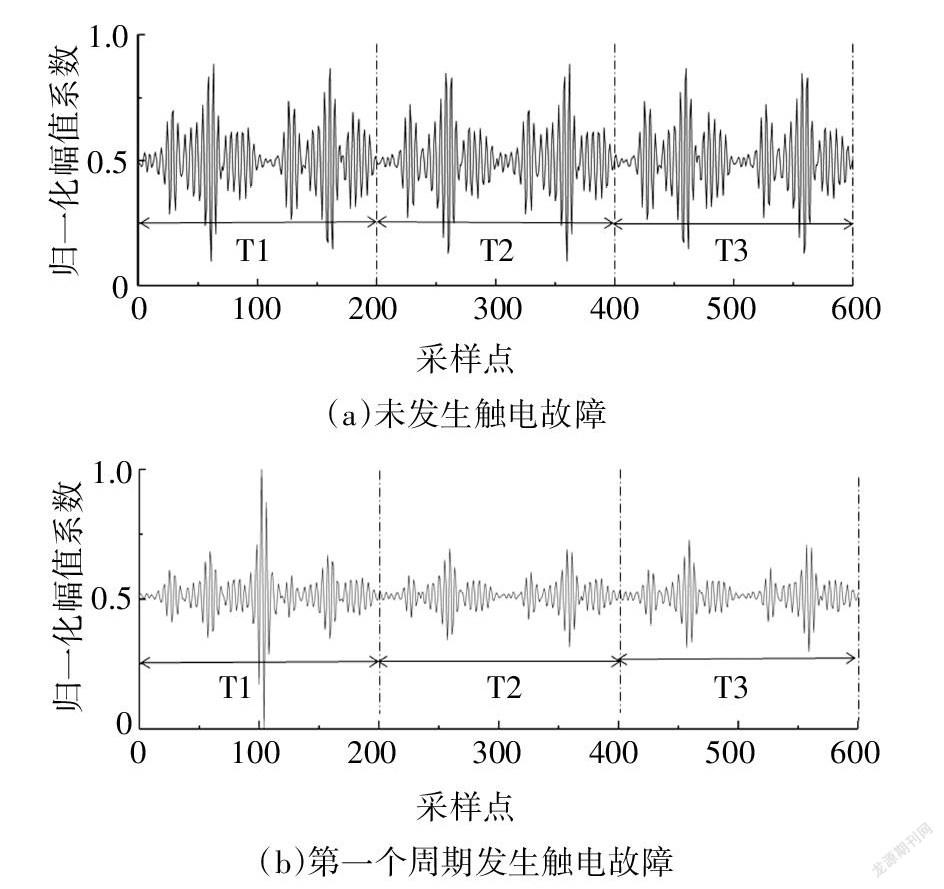
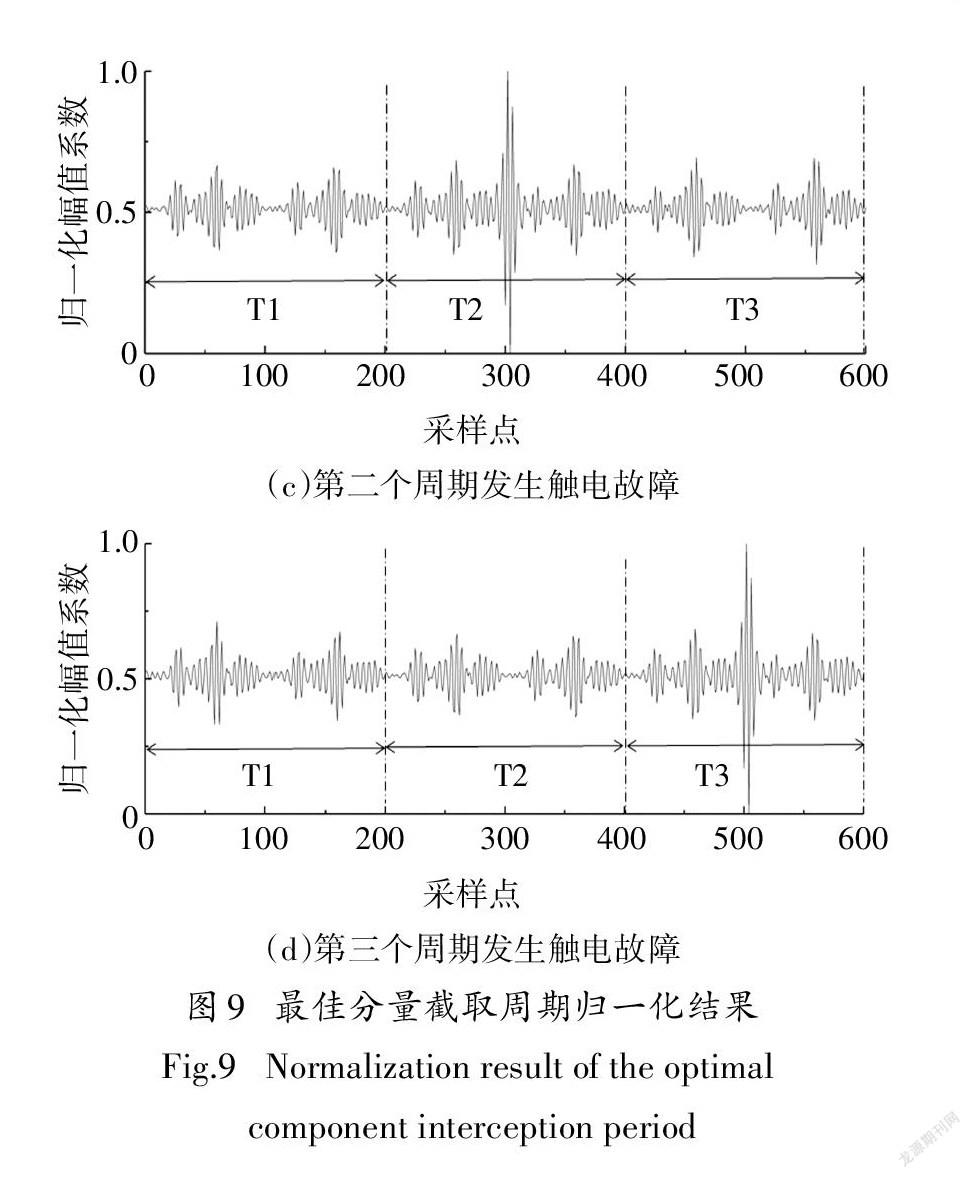
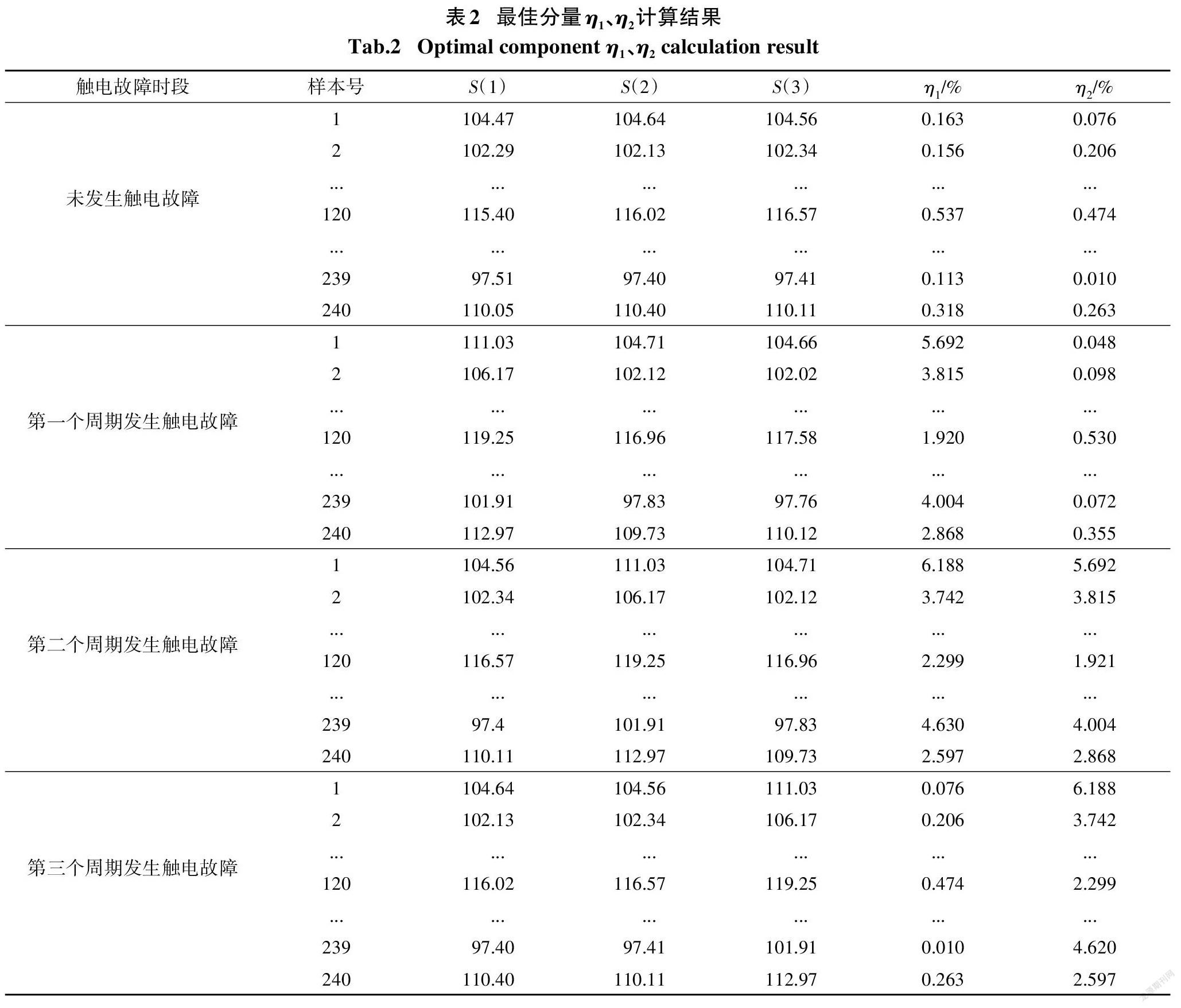
考虑到触电事故具有随机性，选取最佳分量3个周期数据的归一化结果如图9所示，包含四种情况：未发生触电故障（9（a））、触电故障发生在第一个周期（9（b））、触电故障发生在第二个周期（9（c））、触电故障发生在第三个周期（9（d））.对上述触电信号数据样本分别截取四种情况，利用式（9）至式（11）计算各情况下最佳分量电流幅值和的增长率η1、η2，结果如表2所示.

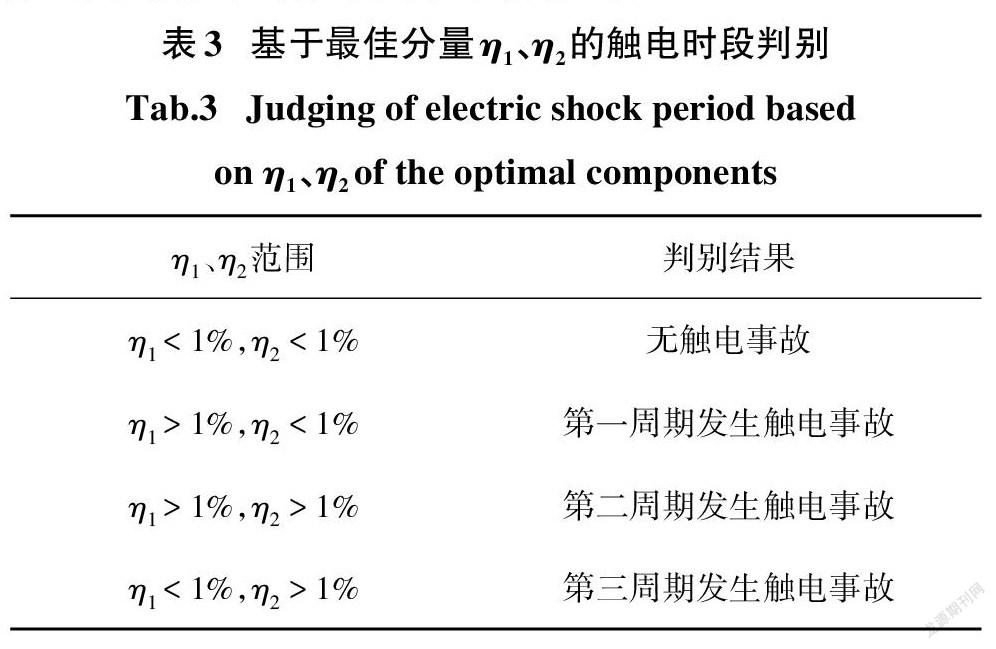
分析表2可知，相比于未发生触电故障的周期，发生触电故障周期的最佳分量电流幅值和较大.当η1、η2至少一个满足大于1%时，均发生触电，否则无触电事故发生，触电时段判别见表3.

4.3仿真与分析

利用4.1节提供的训练样本，根据4.2节获得的最优参数组合[6，280]，将式（14）K取为6重构触电信号，6层剩余电流分量重构作为网络输入，6层触电电流重构作为网络输出，依据3.2节所提算法提取触电电流.

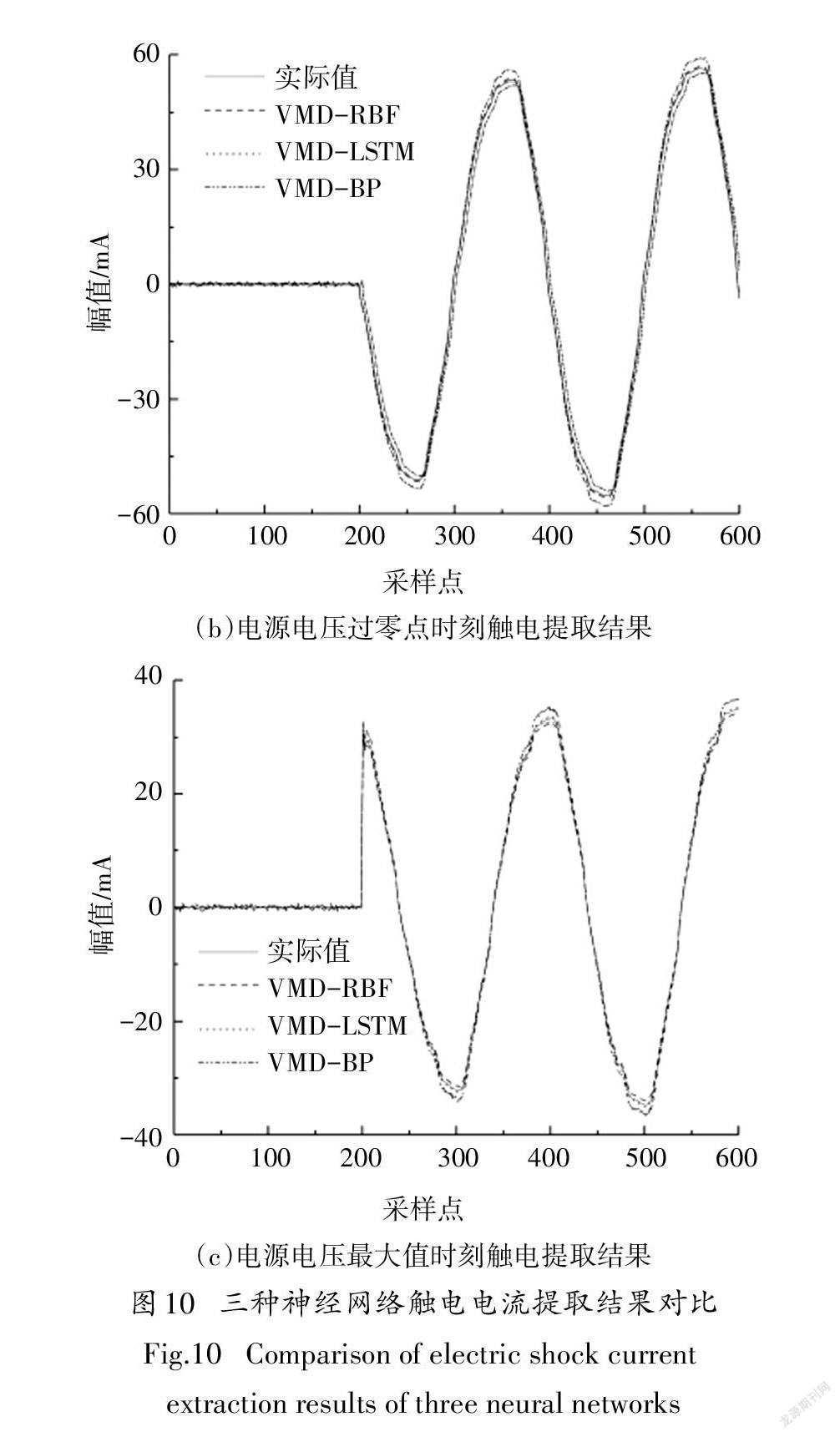
为了验证本文提出的VMD-LSTM检测模型的有效性，采用相同的样本数据作为网络的输入与输出分别建立VMD-BP、VMD-RBF网络模型，BP、RBF网络训练步骤见文献[22].VMD-BP、VMD-RBF网络触电电流提取模型的拓扑结构分别为600-60-600、600-30-600型;VMD-BP、VMD-RBF设定网络的学习率、最大学习次数、目标迭代精度等关键参数均与VMD-LSTM模型相同.各模型三种触电时刻的预测值与真实值如图10所示.三种检测模型40组检测样本的评价指标如图11及表4所示.

分析图11及表4可知：VMD-BP、VMD-RBF、VMD-LSTM三种检测模型相关系数平均值分别为0.9227、0.9576、0.9796，均方根误差平均值分别为0.3341、0.2897、0.2111，VMD-LSTM网络相比于VMD-BP网络、VMD-RBF网络相关系数平均值分别提高了6.2%、2.3%，均方根误差平均值分别降低了36.8%、27.1%.由此可知，基于VMD-LSTM网络的触电信号检测模型具有更高的精度，更接近动物触电物理试验平台采集的动物触电信号.

5结论

本文提出了一种基于VMD-LSTM的触电电流提取方法，根据VMD分解的剩余电流IMF分量提取触电故障特征后，再根据重构后的剩余电流信号结合LSTM算法提取触电电流，实现了触电故障时段判定及触电电流的提取.研究结果表明：

1）通过FOA算法对VMD参数[K，α]寻优获得最优参数组合为[6，280]，利用6层模态分量重构触电信号，避免直接用原始信号检测受高频干扰的影响，保证了触电信号识别精度.

2）根据峭度最大准则选取最佳模态分量，依据突变特性确定触电时段判断阈值.对240组剩余电流信号分析结果表明：当η1<1%，η2<1%时，无触电故障;当η1>1%，η2<1%时，第一个周期发生触电故障;当η1>1%，η2>1%时，第二个周期发生触电故障;当η1<1%，η2>1%时，第三个周期发生触电故障.

3）VMD-LSTM检测模型优于VMD-BP、VMD-RBF检测模型，相关系数平均值分别提高了6.2%、2.3%，均方根误差平均值分别降低了36.8%、27.1%.本文所提方法具有较高的准确性.

参考文献

[1]杜松怀.电力系统接地技术[M].北京：中国电力出版社，2011：25-55.

[2]李春兰，苏娟，杜松怀，等.基于小波分析和BP神经网络的触电信号检测模型[J].农业工程学报，2010，26（S2）：130-134.

[3]关海鸥，杜松怀，李春兰，等.基于有限脉冲反应和径向基神经网络的触电信号识别[J].農业工程学报，2013，29（8）：187-194.

[4]韩晓慧，杜松怀，苏娟，等.基于参数优化的最小二乘支持向量机触电电流检测方法[J].农业工程学报，2014，30（23）：238-245.

[5]刘永梅，杜松怀，盛万兴.基于SVM-神经网络融合反馈的触电电流检测方法[J].电网技术，2020，44（5）：1972-1977.

[6]王金丽，刘永梅，杜松怀，等.基于剩余电流固有模态能量特征的生物触电故障诊断模型[J].农业工程学报，2016，32（21）：202-208.

[7]高阁，李春兰，张亚飞，等.基于正交试验触电试验平台参数优化及触电信号分析[J].中国农机化学报，2019，40（9）：181-188.

[8]DRAGOMIRETSKIY K，ZOSSO D. Variational mode decomposi?tion[J]. IEEE Transactions on Signal Processing，2014，62（3）： 531-544.

[9]贾贝，凌天龙，侯仕军，等.变分模态分解在爆破信号趋势项去除中的应用[J].爆炸与冲击，2020，40（4）：123-131.

[10] LI H，LIU T，WU X，et al.An optimized VMD method and its ap⁃plications in bearing fault diagnosis[J]. Measurement，2020， 1 6 6 ：1 0 8 1 8 5 .

[11]徐长宝，古庭赟，高云鹏，等.基于改进小波阈值函数和变分模态分解的电能质量扰动检测[J].湖南大学学报（自然科学版），2020，47（6）：77-86.

[12]唐成顺，孙丹，唐威，等.基于LSTM循环神经网络的汽轮机转子表面应力预测模型[J].中国电机工程学报，2021，41（2）：451-461.

[13] MEJIA J，AVELAR-SOSA L，MEDEROS B，et al. Prediction of time series using an analysis filter bank of LSTM units[J].Com⁃puters & Industrial Engineering，2021，157：107371.

[14]许淼，刘宏飞，初凯.基于AM-LSTM模型的共享单车时空需求预测[J].湖南大学学报（自然科学版），2020，47（12）：77-85.

[15]张亚男.基于流形学习和优化极限学习机的滚动轴承故障诊断方法研究[D].北京：北京交通大学，2019.

[16]PAN W T.A new Fruit Fly Optimization Algorithm：Taking the fi⁃nancial distress model as an example[J].Knowledge-Based Sys⁃t e m s ，2 0 1 2 ，2 6 ：6 9 - 7 4 .

[17]唐贵基，王晓龙.参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J].西安交通大学学报，2015，49（5）：73-81.

[18]关海鸥，李伟凯，杜松怀，等.基于Hilbert-Huang变换的生物触电电流检测模型[J].农业工程学报，2017，33（14）：202-209.

[19]胡爱军，南冰，任永辉.基于PPCA-EWT的滚动轴承轻微故障诊断[J].振动·测试与诊断，2018，38（2）：365-370.

[20]KRATZERT F，KLOTZ D，HERRNEGGER M，et al. Toward im⁃proved predictions in ungauged basins：exploiting the power of ma⁃chine learning[J]. Water Resources Research，2019，55（12）： 11344-11354.

[21]李春兰，高阁，张亚飞，等.基于局部均值分解（LMD）的单通道触电信号盲源分离算法[J].农业工程学报，2019，35（12）：200-208.

[22]冯瑞龙，王志飞，冯海全，等.基于RBF和BP神经网络的低真空管道高速列车气动阻力预测对比研究[J].真空科学与技术学报，2020，40（9）：827-832.