基于不同模型的吹填软基沉降预测

谭芳　李敏　魏焕卫　白力源

摘要：  针对大面积吹填软土地基长期沉降难以预测的问题，使用静态预测模型和动态预测模型，根据现场沉降观测资料，预测某大面积超载预压工程的沉降量，按照预测步长和输入参数个数的不同设置4种预测任务，对比分析原始样本和插值处理后样本在4种预测任务中的模型可靠度。结果表明，动态模型预测可靠度优于静态预测模型，且动态模型单步预测时BP神经网络模型预测性能优于长短期记忆（long short-term memory，LSTM）网络模型，多步预测时LSTM模型预测性能优于BP神经网络模型。

关键词：  软基; 沉降预测; 三点法; 双曲线法; 长短期记忆网络; BP神经网络

中图分类号：  TP391.99; TU311.3文献标志码：  B

Prediction on settlement of blown soft foundation

based on different models

TAN Fang LI Min WEI Huanwei BAI Liyuana

（a. College of Civil Engineering; b. Subway Protecting Research Institute; c. Key Laboratory of Building

Structural Retrofitting and Underground Space Engineering （Ministry of Education），

Shandong Jianzhu University， Jinan 250101， China）

Abstract： As to the issue that the long-term settlement of large-area hydraulic reclamation soft soil foundation is difficult to predict， the settlement of a large area overload preloading project is predicted based on the field settlement observation data using the static prediction model and dynamic prediction model. Four prediction tasks are set according to the different prediction steps and the number of input parameters. The reliability of original samples and interpolated samples in four prediction tasks model is compared and analyzed. The results show that the prediction reliability of dynamic model is better than that of static model. In the single-step prediction of dynamic model， the prediction performance of BP neural network model is better than that of long short-term memory（LSTM） network model. In multi-step prediction， the prediction performance of LSTM model is better than that of BP neural network model.

Key words： soft foundation; settlement prediction; three-point method; hyperbolic fitting method; long short-term memory network; BP neural network

基金項目：  山东省自然科学基金（ZR2019BEE076）

作者简介： 谭芳（1984—），女，山东烟台人，讲师，博士，研究方向为土体变形机理和岩土工程不确定性，（E-mail）tanfang2017@sdjzu.edu.cn0引言

随着国民经济的提高，沿海地区城市建设迅速发展，采用吹填方式在滨海海岸沉积处进行围海造陆，以缓解城市土地资源紧张问题屡见不鲜。吹填土多以淤泥质土为主，具有含水量高、渗透性小、孔隙比大等特点，不能直接用于工程建设，需要通过堆载预压处理[1-2]提高其承载力，并减小其在建筑载荷作用下的沉降量。在实际工程中，当吹填软基地表沉降量达到施工标准后，需要进行软基沉降预测。目前常见的软基沉降预测方法可以分为3种。

第一种是基于传统固结理论[3-5]进行预测，但是传统固结理论不考虑水平方向渗流对固结的影响，因此预测得到的软基沉降值往往与实测结果差距较大。第二种是基于数值模拟方法[6-9]进行预测，需要选取合适的本构模型，但数值模拟中常用的本构模型不完全适用于吹填软土地基，而且本构模型中涉及诸多土工参数，由于土体扰动的原因，原状土体参数和试验所得参数存在差异，导致预测结果与实测结果差距较大。第三种是基于现场实测数据进行沉降预测，又可分为静态预测和动态预测，其中静态预测方法主要是指以双曲线法[10]、三点法[11]和Asaoka法[12]为代表的曲线拟合法，动态预测方法是基于大数据和人工智能的智能预测[13-16]方法。常见现场实测数据预测方法有灰色模型预测、支持向量机和BP神经网络等。BP神经网络模型是目前软基沉降预测中应用较为广泛的一种预测模型，预测的沉降与实测沉降较为接近。

近年来，长短期记忆（long short-term memory， LSTM）网络在具有时间序列的高度非线性数据映射方面表现优异，因此被广泛应用于深基坑地连墙变形预测[17]、盾构施工引起的变形预测[18]、大范围地表沉降预测[19]等方面，但在大面积吹填软基沉降预测方面鲜有涉及。

本文以某大面积堆载预压工程为背景，构建静态预测模型和动态预测模型预测软基沉降，并对比分析在不同情况下模型的预测精度。

1预测模型

1.1静态预测模型

1.1.1双曲线法

双曲线法假定软基沉降呈双曲线的趋势变化，在载荷稳定后进行拟合预测，沉降量与时间之间的关系为S_t=S₀+t-t₀/A+B（t-t₀） （1

式中：S_t为t时刻的沉降量;t₀为预测起始时间点;A和B分别为（t-t₀）/（S_t-S₀）与t-t₀关系曲线的截距和斜率;S₀为t₀时刻的沉降量。

1.1.2三点法

三点法即传统指数曲线法。等时间间隔在沉降曲线上取3个点，第一个点一般选取在载荷加载完成后，第三个点一般选取在沉降稳定后，三点法的沉降量表达式为

S_t=S_dαe^-βt+S_∞（1-αe^-βt）  （2）

式中：S_t为t时刻的沉降量;S_d为某时间点的瞬时沉降量;S_∞为最终沉降量;α和β为拟合参数。

1.2动态预测模型

1.2.1BP神经网络

BP神经网络是一种多层前馈型神经网络，其基本结构见图1，由输入层、隐含层和输出层组成。

1.2.2LSTM网络模型

LSTM神经网络单元结构示意见图2。图中3个虚线框自左向右依次是遗忘门、输入门和输出门。实线框左侧表示单元输入，右侧表示单元输出，其中细胞元和隐含层是LSTM模型的核心。

通过遗忘门计算前一时刻的细胞元有多少可以保存至当前时刻，

f_t=σ（W_fx_t+U_fh_t-1） （3）

通过输入门计算当前时刻输入信息有多少可以保存至当前时刻，

i_t=σ（W_ix_t+U_ih_t-1）  （4）

a_t=tanh（W_ax_t+U_ah_t-1） （5）

联合遗忘门和输入门更新当前时刻细胞单元，C_t=f_fC_t-1+i_ta_t（6）

通過输出门计算当前时刻细胞元有多少可以保存至隐藏状态，o_t=σ（W_ox_t+U_oh_t-1） （7）

h_t=o_t·tanh（C_t） （8）

式中：f_t、i_t、o_t分别为t时刻的遗忘门、输入门和输出门;x_t为t时刻的输入信息;a_t为t时刻的临时单元状态;W和U为不同门控单元对应的权重矩阵，tanh（ ）为双曲正切函数;σ（ ）为sigmoid函数;C_t和ht分别为t时刻的单元状态和隐藏状态。

2工程背景

2.1工程概况

该工程所处地貌成因类型为河流入海口形成的冲积平原，地势开阔、地形平坦，原始地面高程为1.28～1.46 m，可利用场地南北长约1.8 km，东西宽约2.2 km，可利用面积约370.7公顷，其中A区长760 m，宽670 m。工程勘查显示地层为第四系填土和第四系全新统冲积层。

2.2现场监测数据

选取该工程A区DB7测点监测数据作为原始数据。在堆载期间每5 d监测1次;吹填过程中无法监测，每层吹填完毕具备观测条件之后开始观测;满载后每7 d监测1次，但出现临界状态或异常状况时增加监测次数。DB7测点的沉降曲线见图3。

3沉降预测

3.1原始数据处理

选取DB7测点从2020年3月6日开始至2021年6月1日共计147组沉降监测数据作为原始样本。由于原始样本数据间隔时间不统一，用分段线性插值的方法处理原始样本数据，插值处理后得到452组数据样本。

根据表1构造模型输入样本和输出样本，其中：S为DB7测点在t时刻的沉降监测数据;n为输入参数个数;m为预测信息步长。分别选取n为4和10，m为1和6，构造4个预测任务，具体任务划分见表2。

将输入样本和输出样本的80%作为训练集，剩余20%作为测试集。由于输入参数个数和预测信息的步长不同，不同预测任务对应的训练集和测试集数量有所不同，具体数量见表3。

3.2构建动态预测模型

编写BP神经网络预测模型和LSTM神经网络模型，模型激励函数范围取0～1。输入数据大小会影响模型收敛速度，为提高模型训练速度和预测可靠度，在模型训练前对第3.1节确定的输入数据进行归一化处理，

x_i^*=x_i-min（x_i）/max（x_i）-min（x_i） （9）

式中：max（x_i）和min（x_i）分别为第i个参数对应数据集的最大值和最小值;x_i^*为归一化处理的数值;xi为原始数值。

设置神经网络训练参数。选择合理的模型激励函数，并设置模型训练参数，如隐含层节点数、最大训练次数、学习速率和训练目标误差等。

训练模型并评价预测可靠度。按照上述设置训练模型，对比分析模型预测沉降和实测沉降，以评价模型预测能力。选用平均绝对百分比误差EMAPE评价模型预测能力，EMAPE的值越小，说明预测模型可靠度越高。

3.3构建静态预测模型

采用双曲线法构建沉降预测模型。选择载荷完成后的第一天作为起始时间，根据不同任务选择对应数据区间，计算（t-t₀）/（S_t-S₀）与t-t0关系曲线的截距和斜率，从而构建预测函数进行预测。

构建三点法沉降预测模型。按照不同任务要求选择载荷完成后的第一天作为第一点，选择沉降稳定后沉降曲线上的点为第三点，按照t₃-t₂=t₂-t₁选取第二点，编写计算程序进行预测。

3.4结果分析

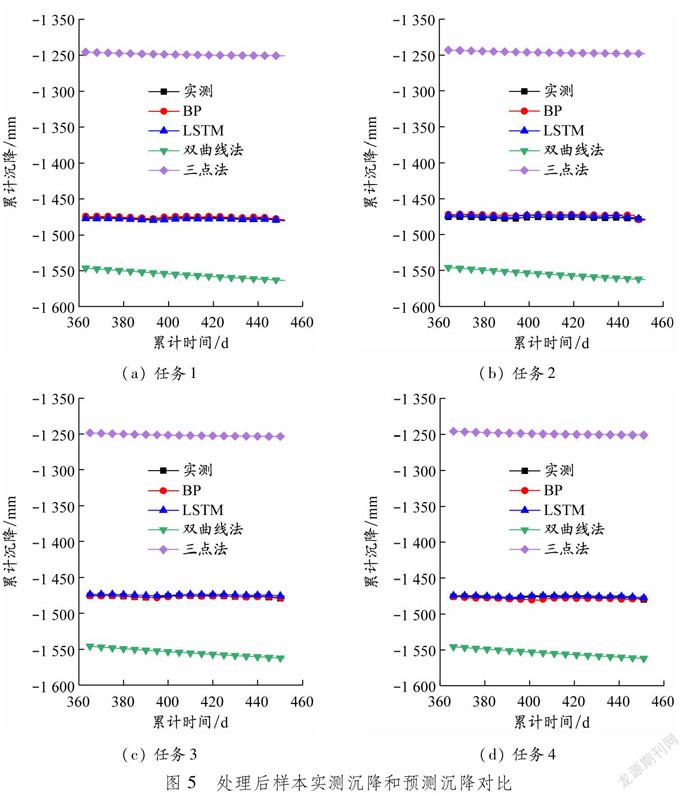
根据表3确定的测试集，使用动态预测和静态预测2种方法进行预测，不同模型预测评价指标见表4。动态预测模型在原始样本中的EMAPE值均大于插值处理后样本的EMAPE值，说明动态预测模型预测精度对样本数据大小较为敏感，样本量越大，动态预测模型预测精度越高。根据预测结果，绘制原始样本和处理后样本在不同任务下的实测沉降和预测沉降进行对比，见图4和5。

综合对比图4和5可知，静态预测模型的预测沉降值与实际沉降值差距较大。图4中双曲线预测结果与实测值较为接近，但实测沉降已经逐渐稳定时，双曲线预测却还在发展中，三点法预测结果比实测结果小约250 mm;图5中三点法预测沉降比实测沉降小约230 mm，双曲线法预测沉降值比实测沉降值大约80 mm，而且还在持续发展中。这是由于在实际工程中，前期沉降数据不能完整反映沉降发展趋势，因此只采用前期沉降预测后期沉降时存在误差。

对比分析表4和图4可知，在输入参数个数相同的情况下，动态单步预测（任务1和3）时，任务3中BP神经网络E_MAPE值相较于任务1下降19%，说明单步预测时BP神经网络模型预测性能优于（a） 任务1（b） 任务2

LSTM神经网络;多步预测（任务2和4）时，任务4中E_MAPE值相比于任务2下降10%，说明多步预测时LSTM模型预测精度优于BP神经网络。

对比分析表4和图5可知，在输入参数个数相同的情况下，动态单步预测（任务1和3）时，任务3的BP神经网络EMAPE值较任务1下降61%;多步預测（任务2和4）时，任务4中LSTM模型E_MAPE值较任务2下降54%，再次验证单步预测时BP神经网络预测性能优于LSTM模型，多步预测时LSTM模型预测性能优于BP模型，而且随着样本数据量的增加，模型预测性能提升，样本数据量对动态预测模型精度有较大影响。

4结论

以某大面积堆载预压工程为背景，采用静态沉降预测模型和动态沉降预测模型分别建立软基沉降预测模型，通过对比模型预测沉降值和实测沉降值可以得出以下结论。

（1）动态预测模型的预测精度远高于静态预测模型。

（2）动态预测模型精度对样本数据量更敏感，LSTM模型和BP神经网络模型在插值处理后样本中的预测性能均优于原始样本中的预测性能。

（3）单步预测时BP神经网络性能优于LSTM模型预测性能，但多步预测时LSTM神经网络预测性能优于BP神经网络。对于不同工程预测需求，应该按照BP和LSTM的适用性，选择合适的算法。

本文动态预测模型输入参数只考虑已有沉降数据，没有考虑土体参数和加载情况的影响，因此模型的普遍适用性未加以证明，下一步应在模型输入参数中增加土体参数和加载情况进行改进。参考文献：

[1]董志良， 张功新， 李燕， 等. 大面积围海造陆创新技术及工程实践[J]. 水运工程，2010， 10： 54-67. DOI： 10.16233/j.cnki.issn1002-4972.2010.10.007.

[2]丁军霞. 直排式真空预压在吹填土地区的应用研究[J]. 铁道工程学报， 2019， 36（1）： 21-25. DOI： 10.3969/j.issn.1006-2106.2019.01.005.

[3]曹文贵， 李鹏， 唐旖旎， 等. 基于孔隙介质特征的地基沉降分层总和分析方法[J]. 中国公路学报， 2016， 29（3）： 1-8. DOI： 10.19721/j.cnki.1001-7372.2016.03.001.

[4]白玮康. 软土地基一维固结理论改进算法及应用研究[D]. 西安： 西安理工大学， 2020.

[5]周健， 周凯敏， 贾敏才， 等. 成层软黏土地基的固结沉降计算分析[J]. 岩土力学， 2010， 31（3）： 789-793. DOI： 10.16285/j.rsm.2010.03.039.

[6]崔凯， 杨文恒. 软土路基沉降的联合法预测研究[J]. 西南交通大学学报， 2017， 52（5）： 926-934. DOI： 10.3969/j.issn.0258-2724.2017.05.012.

[7]胡群革， 严俊， 魏迎奇， 等. 海滨深厚软基上围垦造地工程固结沉降分析方法研究[J]. 中国水利水电科学研究院学报， 2016， 14（1）： 67-72. DOI： 10.13244/j.cnki.jiwhr.2016.01.011.

[8]史静， 任杰， 杨杰. 基于软土双屈服面模型的滨海路基沉降预测分析[J]. 公路， 2020， 65（8）： 80-84.

[9]徐成华， 谈金忠， 骆祖江， 等. 地铁盾构施工引发地面沉降三维流固全耦合数值模拟预测[J]. 南京大学学报（自然科学）， 2019， 55（3）： 409-419. DOI： 10.13232/j.cnki.jnju.2019.03.008.

[10]李国维， 杨涛， 宋江波. 公路软基沉降双曲线预测法的进一步探讨[J]. 公路交通科技， 2003（1）： 18-20. DOI： 10.3969/j.issn.1002-0268.2003.01.005.

[11]潘林有， 谢新宇. 用曲线拟合的方法预测软土地基沉降[J]. 岩土力学， 2004， 25（7）： 1053-1058. DOI： 10.16285/j.rsm.2004.07.010.

[12]黄广军. Asaoka法预测软土地基沉降时存在的问题和对策[J]. 岩土力学， 2016， 37（4）： 1061-1065. DOI： 10.16285/j.rsm.2016.04.019.

[13]彭涛， 杨岸英， 梁杏， 等. BP神经网络-灰色系统联合模型预测软基沉降量[J]. 岩土力学， 2005， 26（11）： 119-123. DOI： 10.16285/j.rsm.2005.11.025.

[14]俞亚南， 张仪萍， 高庆丰. 成层软土地基黏弹性参数反演及沉降预测[J]. 土木工程学报， 2005， 38（7）： 112-115. DOI： 10.3321/j.issn：1000-131X.2005.07.022.

[15]范思遐， 周奇才， 熊肖磊， 等. 基于多核模式的隧道沉降预测[J]. 岩土力学， 2013， 34（S2）： 291-298. DOI： 10.16285/j.rsm.2013.s2.047.

[16]郭晓君， 刘思峰， 方志耕， 等. 灰色GM（1， 1， tα）模型与自忆性原理的耦合及应用[J]. 控制与决策， 2014， 29（8）： 1447-1452. DOI： 10.13195/j.kzyjc.2013.0707.

[17]赵华菁， 张名扬， 刘维， 等. 基于神经网络算法的深基坑地连墙变形动态预测[J]. 地下空间与工程学报， 2021， 17（S1）： 321-327.

[18]李洛宾， 龚晓南， 甘晓露， 等. 基于循环神经网络的盾构隧道引发地面最大沉降预测[J]. 土木工程学报， 2020， 53（S1）： 13-19. DOI： 10.15951/j.tmgcxb.2020.s1.003.

[19]劉青豪， 张永红， 邓敏， 等. 大范围地表沉降时序深度学习预测法[J]. 测绘学报， 2021， 50（3）： 396-404.（编辑武晓英）