基于预报方程的我国近海阵风预报*

胡海川 刘 珺 林 建

1 国家气象中心，北京 100081 2 中国气象局公共气象服务中心，北京 100081

提 要： 阵风对航运及海上生产作业影响重大，但目前海上阵风客观预报产品较少且时间分辨率低。为进一步丰富海上阵风客观预报产品，提高海上阵风预报准确率，基于2016—2019年实况观测数据及ERA5再分析数据，采用多元回归方法建立我国近海逐小时阵风预报方程，并利用2020年ECMWF确定性模式数据进行预报试验。对比2020年ECMWF确定性模式中的阵风预报及阵风系数法预报产品，基于多元回归方法的阵风预报方程考虑了平均风速项、近地面层湍流作用项以及对流作用项，具有明确的物理意义和统计学意义，对阵风有更好的拟合效果。在8～9级阵风预报中，多元回归方法预报的平均误差、平均绝对误差低于ECMWF确定性模式中的阵风预报，在冷空气大风天气过程中的预报效果优于ECMWF确定性模式，同时该方法也能够反映出台风影响下的阵风情况，可为我国近海阵风预报提供参考。

引 言

阵风是指在数秒内风速的平均，在地面气象观测中以3 s的平均值来反映阵风的大小。当阵风大于某一阈值时，就会对交通运输、房屋建筑、生产生活产生巨大影响，准确的预报阵风可以有效地降低生命财产损失。阵风被认为是某些大尺度低频结构与其上强湍流脉动叠加形成的，当地面风速较强时，叠加在平均流动之上的脉动不仅包含随机的湍流脉动，同时还会出现边界层上层阵风向下传递的过程(程雪玲等，2007；2016)。在业务预报中，由于缺乏高精度的实况观测，且难以实现对随机湍流脉动及边界层上层阵风向下传递作用的定量刻画，使得阵风预报一直是预报中的难点问题(黄世成等，2009；Cheng et al，2012；刘辉志等，2013)。阵风客观预报方法可分为基于统计的预报方法和基于物理过程的预报方法。在基于统计的阵风预报方法中，阵风系数法是一种计算简单且常用的方法，即通过计算持续时间内最大风速与其所在时间尺度的平均风速的比值来表征风速脉动强弱，进而估算出最大阵风值(Adams，2004)。在不同的下垫面、海拔高度及天气系统下，阵风系数差异明显，因此诸多学者也对阵风系数进行更深入研究以取得更为准确的阵风预报(董双林，2001；李倩等，2004；Paulsen and Schroeder，2005；Shu et al,2015；周福等，2017)。此外，基于统计的阵风预报方法还有多模式集成、神经网络、回归、经验相似预报等(曾瑾瑜等，2015；Kretzschmar et al,2004；赵金霞等，2014；胡波等，2014；2019)。阵风估计(wind gust estimate,WGE)方法是一种基于物理过程的预报方法，认为阵风是由于边界层中空气块湍流动能的垂直分量克服浮力后，偏转向下到达地面后形成的(Brasseur,2001)。WGE方法不仅考虑了平均风和大气湍流结构，还提供了可能出现的阵风量级范围，因此有学者基于 WGE 方法的阵风模型开展预报试验(Pinto et al，2009；Chan et al，2011)。基于统计的预报方法与基于物理过程的预报方法各有优劣，将两者进行结合可以有效提高阵风的预报准确率(Patlakas et al，2017)。

相比于平均风，阵风对于海上航运安全及生产作业的影响更大，但海上观测资料严重缺乏，无论是海面还是高空数据都很稀少，这不仅使得数值模式难以对海上气象要素进行准确刻画，同时也限制了海上客观预报方法的开展(季晓阳等，2005)。造成我国近海大风天气过程的天气系统复杂，主要可分为冷空气型、温带气旋型和热带气旋型三类，其中冷空气型又包括小槽东移型、小槽发展型和横槽转竖型；温带气旋又包括东海气旋型、黄渤海气旋型和蒙古气旋型(吕爱民等，2018)。由于海洋观测资料的稀缺及影响系统的复杂，现有诸多阵风预报方法并不能够很好地适用于海上，因此需要开展我国近海阵风预报方法的研究工作。目前业务中的海上阵风预报主要参考欧洲中期天气预报中心(ECMWF)的阵风预报产品，该产品是在预报时段内(3 h或6 h)10 m最大平均风速的基础上考虑湍流和对流作用计算而得(Bechtold and Bidlot，2009)，计算公式如下：

Fgust=F10+Cugnu*+Cconvmax(0,U850-U950)

(1)

式中：Fgust为阵风风速；F10为预报时段内水平最大平均风速；Cugn为常数项，取值为7.71；u*为摩擦速度；Cugnu*为由湍流作用造成的阵风；Cconv为常数项，取值为0.6；max(0,U850-U950)为预报时段内850 hPa与950 hPa间最大正风速切变；Cconvmax(0,U850-U950)为由对流作用造成的阵风。虽然该公式既包含了统计系数，又兼顾了物理过程，但公式中涉及的风速均是预报时段内的最大值或最小值，并不是模式中通常输出的时刻风速，因此业务中难以利用该公式来进行更高时间分辨率的阵风预报。

在海上观测资料稀缺的情况下，我国近海风速客观预报方法主要是基于统计数值模式对于沿岸、近海、海岛站点预报的平均误差特性，将其适用于近海的思路开展的。基于该思路的客观预报方法能够有效提升数值模式对于大量级风速的预报能力并取得较好的应用效果(胡海川和周军，2019；胡海川等，2021)。海洋下垫面均一，在很大程度上降低了海上阵风预报的难度(Letson et al，2018)，本文将利用实况观测数据及再分析数据，选取沿岸、近海、海岛代表站点建立我国近海逐小时阵风预报方程并进行预报试验。

1 资料和方法

本文利用2016—2019年地面实况观测数据中的逐小时风速数据与小时内极大风数据，ERA5再分析数据中的1 000、925、850 hPa风场数据建立逐小时阵风预报模型。利用2020年ECMWF确定性模式10 m风场预报数据，3 h内最大阵风预报数据，1 000、925、850 hPa风场预报数据进行预报试验及效果对比。模式数据的预报时效为12～120 h，间隔为12 h，空间分辨率为0.1°×0.1°。如图1所示，本研究共选取了沿岸、近海、海岛共计41个代表站点，所选站点基本覆盖我国东部沿岸和近海海域，以便建立的阵风预报方程可以适于我国近海。所选站点平均海拔高度为5 m，最大海拔高度为14 m，因此未对实况风速数据进行高度订正。使用平均风速计算阵风时，平均风速采样时段必须大于3分钟才具有代表性(胡波，2019)。但业务中使用的数值模式数据，其采样时段并不输出大于3分钟及以上的平均风速，为了能够将所建立的预报模型进行更好的应用，文中利用时刻风速近似代替平均风速。

本文第三节使用偏相关系数表征自变量与因变量之间的关系，当偏相关系数为一阶时(即影响因子为两个)，控制其中一个自变量的影响，计算另一个自变量与因变量之间的关系，计算公式如下：

(2)

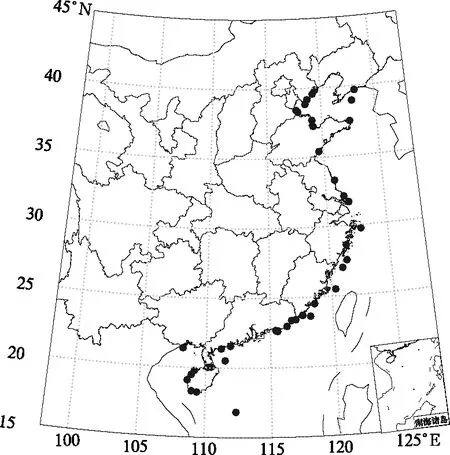
图1 沿岸及近海代表站点分布Fig.1 Distribution of representative stations on coast and offshore

式中：rab_c为控制自变量c影响的情况下，因变量a和自变量b之间的相关系数；rab、rac、rbc分别表示a、b、c间的简单相关系数。当自变量为三个时，需要控制其中两个自变量的影响，计算另一个自变量与因变量的关系，因此需要计算二阶偏相关系数，计算公式如下：

(3)

式中：rab_cd为在控制因子c、d影响的情况下，因变量a与自变量b之间的相关系数。文中垂直风切变为高层风速值减去低层风速值，当其差值大于零时为正切变，小于零时为负切变。

2 预报因子

2.1 平均风速

一般情况下，阵风随着平均风的增加而增大。2016—2019年的实况观测数据显示，当平均风速为22～24 m·s-1时，阵风为25～36 m·s-1；当平均风增大到28～30 m·s-1时，阵风可以达到35～45 m·s-1。阵风系数可以很好地反映出阵风随平均风速增大而增大的一般规律，但简单地利用阵风系数法进行阵风预报时会出现大量漏报的情况。利用2016—2019年的实况观测数据，采取最小二乘法求解出不同平均风速下的阵风系数(图2)，并将该系数带入实况观测的平均风中进行阵风回算。通过对回算数据的检验发现，当实况观测的阵风为6级时，31.9%的回算值偏小2 m·s-1以上；当实况观测的阵风为10级时，48.3%的回算值偏小2 m·s-1以上；当实况观测的阵风为12级时，回算值偏小

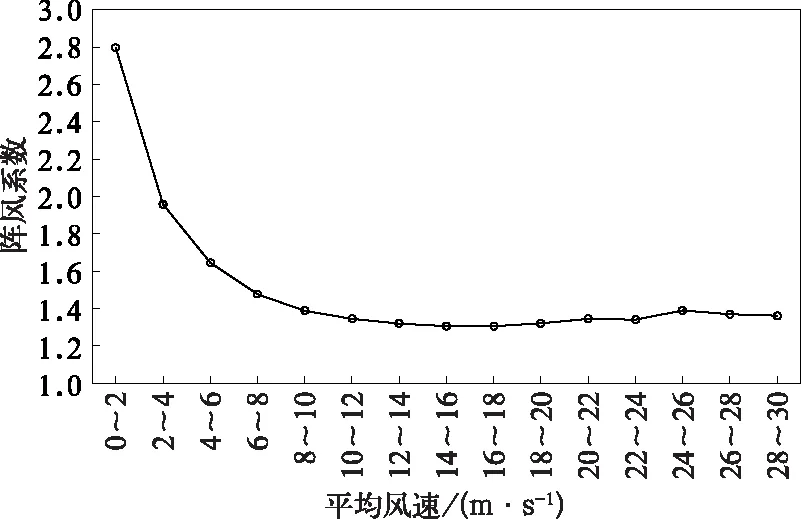
图2 2016—2019年不同平均风速下的阵风系数Fig.2 Gust factors at different average wind speeds from 2016 to 2019

2 m·s-1以上的比例高达57.5%。

2.2 近地面层垂直风切变

近地面层垂直风切变的增加可以使湍流运动增强(杜群等，2017)，因此近地面层垂直风切变也会直接影响到地面阵风。近地面层高度一般为几十米(盛裴轩等，2003),因此本文中以1 000 hPa风速与10 m风速差近似表示近地面层垂直风切变。

图3为平均风速分别在10～12 m·s-1、14～16 m·s-1时，近地面层正或负垂直风切变下的阵风增幅。通过综合对比箱线图中的中位数、第75%分位数、最大值可以发现，在近地面层垂直风切变为正的情况下阵风增幅要明显大于近地面层垂直风切变为负的情况。在相同平均风速的情况下，近地面层的正垂直风切变能够激发活跃的湍流作用，使地面阵风增强，因此近地面层垂直风切变是构建阵风预报方程的重要因子。

2.3 低层垂直风切变

较强的垂直风切变有利于对流风暴的发展，对流风暴中的下沉气流会使地面出现较大的阵风(何娜等，2020；朱义青和高安春，2021)。Brasseur(2001)在WGE方法研究中指出，当强对流天气发生时，对流层中的下沉气流会影响地面的阵风。但强对流天气中的下沉气流对地面阵风的影响范围小、发生频率低、定量计算难度大，因此大多数的WGE方法主要是基于边界层中的因子进行的，以取得较好的适用性(胡波，2019)。ECMWF确定性模式的阵风预报产品也仅仅将预报时段内850 hPa与950 hPa间最大正垂直风切变作为可能由对流影响造成的阵风。本文构建的阵风预报方程拟采用850 hPa与925 hPa或850 hPa与1 000 hPa的垂直风速差作为低层垂直风切变项，以表征对流作用影响下的阵风。

通过以上分析，初步确定平均风速(F10)、1 000 hPa与10 m的风速差(F1 000-F10)以及850 hPa与925 hPa或850 hPa与1 000 hPa的垂直风速差(F850-F925或F850-F1 000)作为阵风预报因子。

3 偏相关分析

简单相关系数只能表明两个变量间的共性联系，当多个自变量均对因变量有影响时，不能够只根据简单相关系数就推断自变量与因变量之间的关系，需要考虑这种相关性是否由其他变量的变化所引起的。在多元回归中应利用偏相关分析来明确自变量与因变量之间的关系，即把其他影响因子作为常数，暂时不考虑其他要素的影响，单独研究两个要素之间的关系。为进一步明确预报因子与阵风之间的关系，确定低层垂直风切变项的具体层结，需要对所选预报因子与阵风进行偏相关分析。

利用2016—2019年实况观测及再分析数据，计算了平均风速、近地面层垂直风切变、低层垂直风切变分别选取F850-F925、F850-F1 000情况下的偏相关系数。低层垂直风切变选取F850-F1 000时的偏相关系数要略高于F850-F925，因此本文最终选取F850-F1 000作为低层垂直风切变项，以表征对流作用下的阵风。

图3 不同平均风速在近地面层正负垂直风切变下的阵风增幅 (a)平均风速为10～12 m·s-1,(b)平均风速为14～16 m·s-1Fig.3 The gust increment of different average wind speeds under the positive and negative vertical wind shear near the ground layer (a) average wind speed 10-12 m·s-1, (b) average wind speed 14-16 m·s-1

对偏相关系数的计算表明(表1)，无论在何种垂直风切变条件下，平均风速对于阵风的影响均是最大的。当近地面层垂直风切变为正值时偏相关系数分别为0.39和0.50，明显高于近地面层垂直风切变为负值时的0.09和0.016，表明近地面层正的垂直风切变对阵风有一定影响，而负的垂直风切变对阵风影响较小，甚至无影响。低层垂直风切变与近地面层垂直风切变对于阵风影响的情况基本相同，但由于对流天气发生概率低且对流层上层阵风下传作用的不确定性大，因此低层垂直风切变的影响相对较小。在近地面层垂直风切变为正、低层垂直风切变为负的情况下，近地面层正的垂直风切变与阵风间的简单相关系数仅为-0.046，而偏相关系数为0.50。偏相关分析能够更为清楚地揭示要素间的内在联系，为预报方程的建立提供基础。以上相关性检验均通过水平双侧0.01显著性检验。

表1 不同风速切变下预报因子与阵风间的偏相关系数Table 1 Partial correlation coefficients between predictors and gusts under different vertical wind shears

4 预报方程

利用最小二乘法求解以上三个预报因子在不同垂直风切变条件下的回归系数。在不同垂直风切变条件下，平均风速的回归系数量级基本相当，在1.290～1.379。当近地面层垂直风切变为正值时对应的回归系数分别为0.482与0.588；当低层垂直风切变为正值时对应的回归系数分别为0.146和0.185。当近地面层或低层垂直风切变为负值时对应的回归系数小于垂直风切变为正时。由于在不同垂直风切变条件下，平均风速所对应回归系数基本相当，近地面层或低层垂直风切变为正值时所对应的回归系数差异不大，因此可以将平均风速在不同风速切变条件下的系数进行平均，将近地面层与低层垂直风切变在正值时所对应的回归系数进行平均。

根据上述系数建立的多元回归阵风预报方程如下所示：

G=aF10+b(F1 000-F10)+

c(F850-F1 000)

(4)

式中：a为平均风速系数(1.343)，b为湍流作用系数(0.535)，c为对流作用系数(0.165 5)；其中湍流作用项(F1 000-F10)和对流作用项(F850-F1 000)均大于0，若上述两项中某一项小于等于0，则该项将不被考虑出现在预报方程之中。

多重共线性问题是多元回归中的一个不可忽视的问题，严重的共线性问题会导致回归系数的符号与实际情况相反，甚至出现无法求解回归系数的情况。本文所选预报因子在个别垂直风切变条件下会出现彼此间存在中等相关性的情况，但考虑到预报因子具有明确的物理意义，且回归系数与实际情况相符，并不会出现由于样本量的更改导致回归系数不稳定的情况，因此本文忽略预报因子间的共线性问题。 阵风预报方程中涉及1 000 hPa风速，在2016—2019年构建预报方程的数据中，当出现1 000 hPa 高度低于10 m时，1 000 hPa与10 m风速差为正值的情况仅占2.3%，其中地面平均风速在1～3 m·s-1时出现此情况的比例高达61%。在1 000 hPa 高度低于10 m时，850 hPa与1 000 hPa风速差为正值的比例仅占1.8%，且68%的比例集中在5 m·s-1风速以下，对整体拟合效果影响较小。总体上，当1 000 hPa与10 m、850 hPa与1 000 hPa间的风速差为正值时，1 000 hPa高度通常大于10 m。

为验证阵风预报方程的拟合效果，对比基于多元回归的阵风预报方程与阵风系数法的拟合误差，阵风系数如图2所示，拟合误差计算公式如下所示：

(5)

图5分别为2016—2019年的12月、1月、2月山东威海鸡鸣岛浮标与7—9月广东茂名浮标出现8级及以上阵风时，多元回归方法和阵风系数法的绝对误差散点图。由图可以看出，当阵风系数法预报的误差较小时，多元回归预报的误差也较小，因此原点附近散点分布较为密集。当阵风系数法预报的误差较大时，散点主要集中在对角线左侧，表明多元回归方法预报的误差要明显小于阵风系数预报法。相比于阵风系数法，无论在冬季的北方海域或是夏季的南方海域，多元回归方法都能够对阵风有更好的拟合效果。

5 应用分析

为进一步验证多元回归方法阵风预报的应用效果，利用2020年ECMWF确定性模式10 m风场预报数据、1 000、925、850 hPa风场预报数据进行预报试验，并分别与阵风系数法及ECMWF确定性模式中的阵风预报进行预报误差对比。选取冷空气大风天气过程及台风大风天气过程，对比多元回归方法的阵风预报与ECMWF确定性模式中阵风预报产品的预报效果。

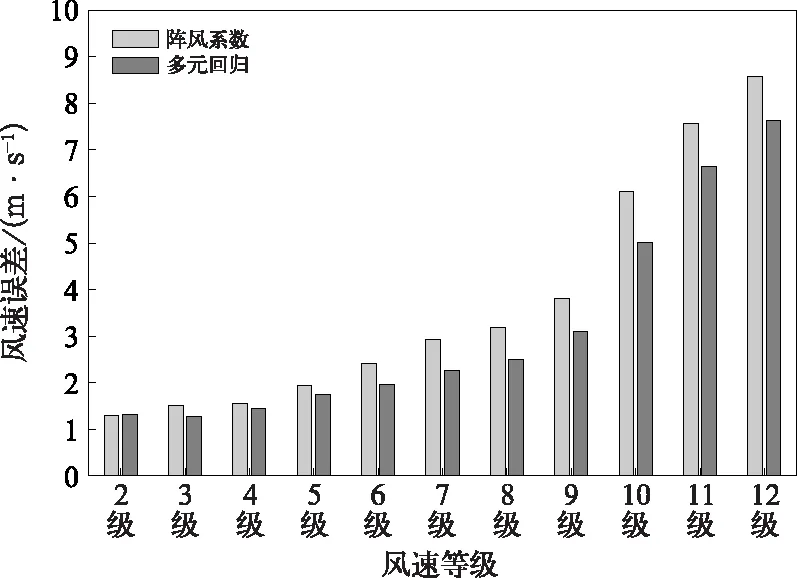
图4 2016—2019年多元回归方法 与阵风系数法拟合误差Fig.4 Fitting errors between the multiple regression method and the gust factor method from 2016 to 2019

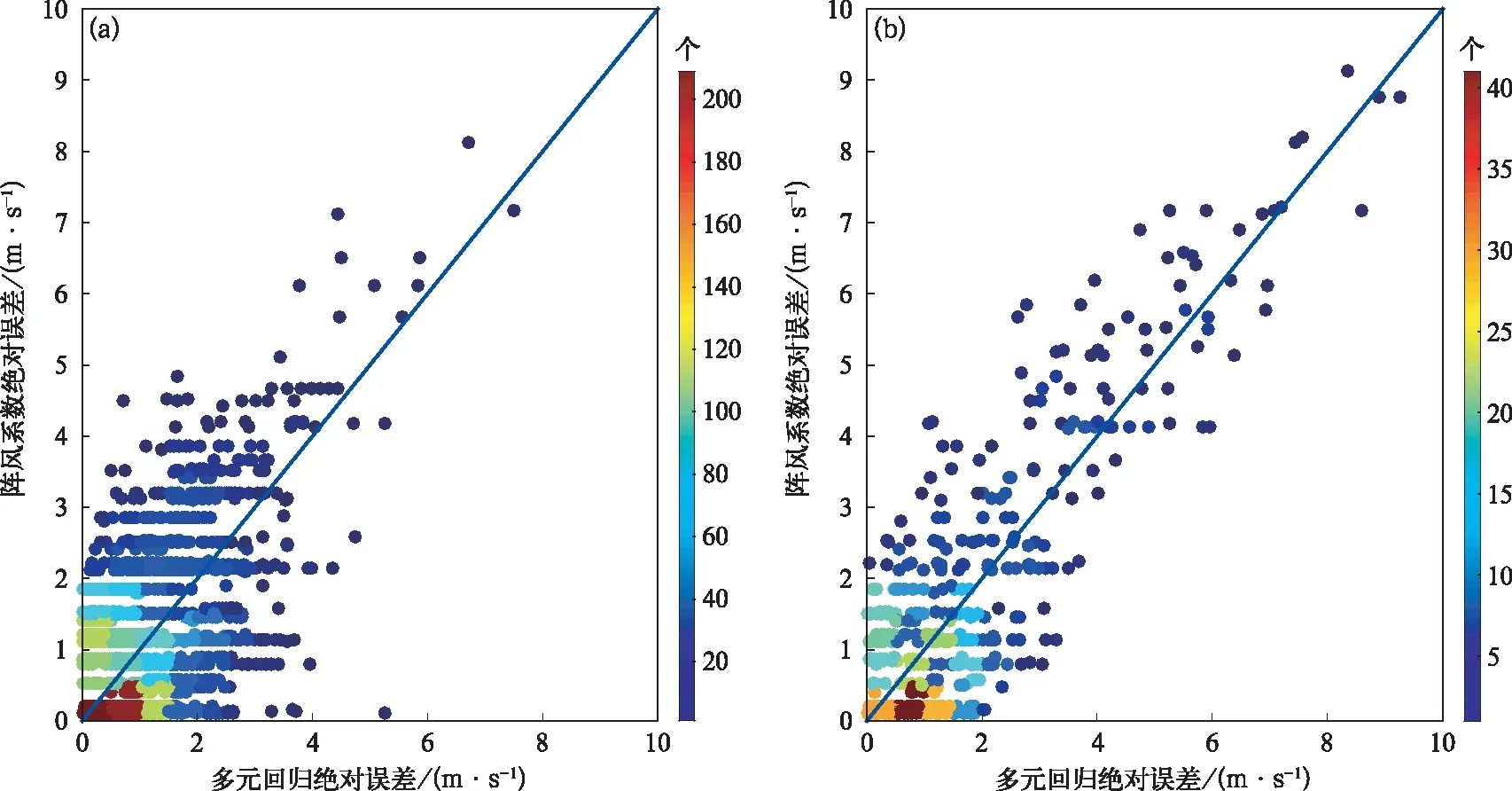
图5 2016—2019年多元回归方法与阵风系数法绝对误差散点图 (a)12月、1月、2月威海鸡鸣岛浮标出现8级及以上阵风, (b)7—9月茂名浮标出现8级及以上阵风Fig.5 Absolute error scatter plots of the multiple regression method and the gust factor method in 2016-2019 (a) the gust of scale 8 and above on the buoy in Jiming Island, Weihai in December, January and February, (b) the gust of scale 8 and above on the buoy in Maoming from July to September

5.1 预报误差对比

ECMWF确定性模式中10 m风速预报存在着明显的系统性误差，即小量级风速预报偏大、大量级风速预报偏小(胡海川等，2021)，基于该产品的阵风系数法的阵风预报也存在着相同的系统性误差。本文基于多元回归的阵风预报及阵风系数法的预报均是逐小时预报，其所对应的实况样本相同，图6给出了2020年基于ECMWF确定性模式数据的阵风系数法与多元回归方法在24 h预报时效的平均误差对比。从图6中可以看出，多元回归方法阵风预报的平均误差总体上小于阵风系数法，阵风系数法对于3级阵风预报的平均误差为2.77 m·s-1，而多元回归预报的平均误差为1.79 m·s-1；对于9级阵风，多元回归方法的平均误差仅为-1.52 m·s-1，而阵风系数法的平均误差达-3.35 m·s-1。由于多元回归方法的阵风预报不仅考虑了平均风速，同时也考虑了近地面层风速切变和低层风速切变，降低了模式10 m风速预报系统性误差的影响，因而其出现小量级风速预报偏大、大量级风速预报偏小的情况较阵风系数法有明显改善。随预报时效的增加，两种方法对大量级阵风预报偏小的程度均增加，但多元回归预报的效果要优于阵风系数法。在 120 h预报时效，阵风系数法对8级、9级阵风预报的平均误差分别为-3.36 m·s-1、-4.86 m·s-1，多元回归方法则分别为-2.18 m·s-1、-3.25 m·s-1。

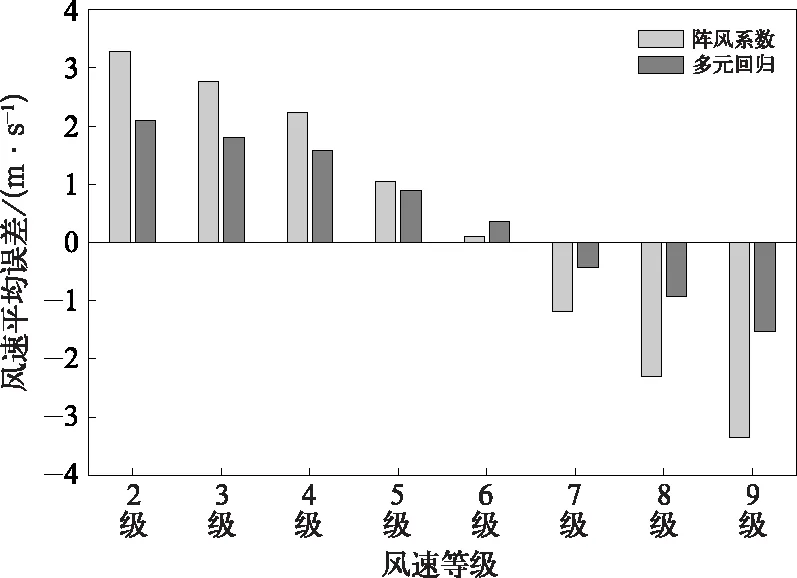
图6 2020年基于ECMWF确定性模式数据的 阵风系数法与多元回归方法24 h预报平均误差Fig.6 Average error between the gust factor method and the multiple regression method of 24 h forecast based on ECMWF deterministic model data in 2020

ECMWF确定性模式中的阵风预报产品为3 h内最大阵风值，而基于多元回归方法的阵风预报是逐小时内的阵风预报。当阵风量级较小时，两种阵风预报产品所对应的实况样本量会存在较大差异，因此仅对比两者对于大量级风速的预报误差。图7为2020年实况出现8～9级阵风时ECMWF确定性模式中阵风预报与基于多元回归方法阵风预报的平均误差对比。由图7可见，对于各个预报时效、各个风速量级，两者预报误差均为负值，但基于多元回归方法的阵风预报的平均误差始终小于ECMWF确定性模式中的阵风预报。

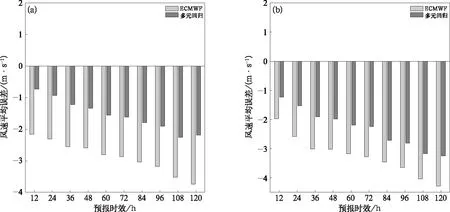
图7 2020年ECMWF确定性模式阵风预报与多元回归阵风预报平均误差 (a)实况出现8级阵风,(b)实况出现9级阵风Fig.7 Average error between the ECMWF deterministic model gust forecast and the multiple regression gust forecast in 2020 (a) observed scale 8 gust, (b) observed scale 9 gust

平均误差的减少不足以证明多元回归方法对于大量级风速预报的效果优于ECMWF确定性模式，过量的空报同样可以使平均误差有所降低。为进一步验证基于多元回归方法的阵风预报效果，计算了2020年实况出现8～9级阵风时基于多元回归方法的阵风预报与ECMWF确定性模式中阵风预报的平均绝对误差(图8)。如图8所示，除多元回归方法在108 h预报时效对9级阵风预报的平均绝对误差略高于ECMWF确定性模式外，其他预报时效的平均绝对误差均要小于ECMWF确定性模式中的阵风预报。

对比2020年多元回归方法、阵风系数法以及ECMWF确定性模式中阵风预报产品的误差表明，多元回归方法降低了对数值模式10 m风速的依赖，因此对小风预报偏大、大风预报偏小的情况较阵风系数法有明显改善，大量级风速预报效果优于ECMWF确定性模式的阵风预报。

5.2 冷空气大风个例对比

2020年12月12—15日，受冷空气影响，我国近海出现了一次明显大风天气过程，其中台湾海峡的阵风达10级(周冠博等，2021)。图9a为ECMWF确定性模式在12月12日08时的48 h阵风预报，虽然模式中的阵风预报是3 h内的最大阵风风速，但对于14日08时台湾海峡及附近海域9～10级阵风预报仍略显偏弱。图9b为多元回归方法在12日08时的48 h阵风预报，多元回归方法预报出现20 m·s-1以上风速的范围大于ECMWF确定性模式，同时在台湾海峡预报的风速值也大于ECMWF确定性模式，与实况观测结果更为接近。

5.3 台风大风个例对比

2020年第8号台风巴威在台湾以东洋面生成后一路北上，先后影响我国东海、黄海、渤海等海域。8月25日20时，台风巴威中心位于我国东海海域，中心附近最大风力为42 m·s-1(强台风级)。图10分别为ECMWF确定性模式及多元回归方法在24日20时的24 h阵风预报，图中风羽为实况观测。在台风中心附近位置，ECMWF确定性模式预报出60 m·s-1以上的阵风，而多元回归方法仅预报出52 m·s-1的阵风。对于台风外围影响区域，多元回归方法的阵风预报的大风范围较ECMWF确定性模式略有偏小，但与实况观测更为接近。ECMWF确定性模式中的阵风是基于3 h内最大风速计算得到，而多元回归方法主要是根据模式预报的时刻风计算得到，由于人们对台风结构和强度变化的复杂性以及海陆气相互作用缺乏足够的认识，以及模式分辨率较低等因素的影响(端义宏等，2012；王晨稀，2014)，数值模式对于台风中心附近最大风速预报会有所偏弱，因此在台风中心附近区域会出现多元回归方法预报出阵风小于ECMWF确定性模式的情况。

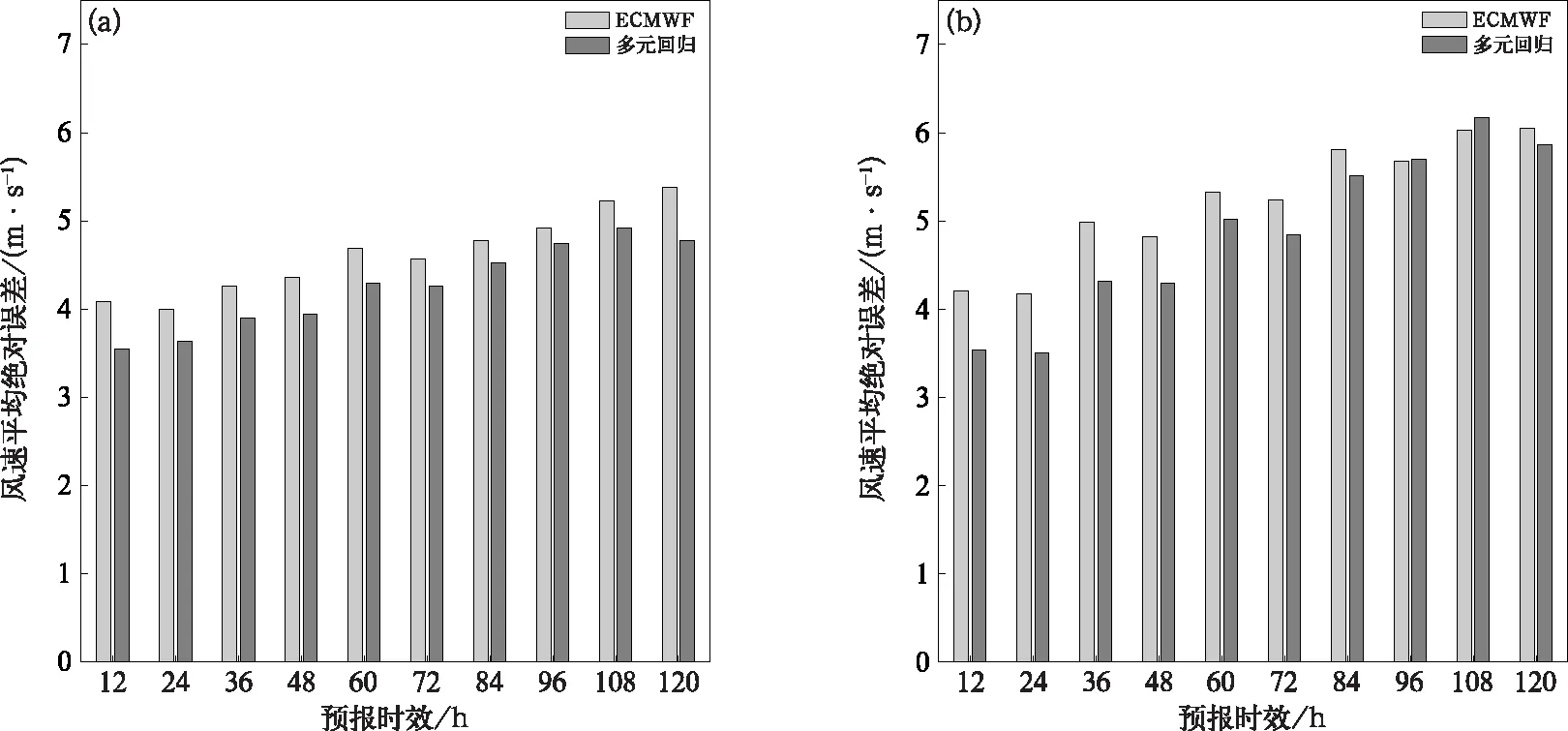
图8 同图7，但为平均绝对误差Fig.8 Same as Fig.7, but for mean absolute error

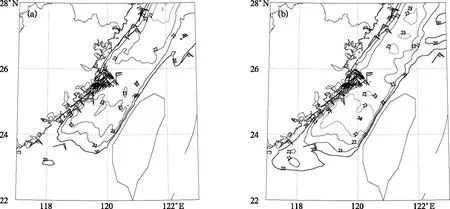
图9 2020年12月12日08时48 h阵风预报(等值线，数字)及14日08时的小时 最大阵风风速观测实况(风羽≥20 m·s-1) (a)ECMWF确定性模式3 h内最大阵风预报,(b)基于多元回归方法的1 h最大阵风预报Fig.9 The 48 h gust forecast (contour, number) at 08:00 BT 12 and the observation (barb, ≥20 m·s-1) of the peak gust wind speed at 08:00 BT 14 December 2020 (a) the 3 h maximum gust forecast of ECMWF deterministic model, (b) the 1 h maximum gust forecast by the multiple regression method

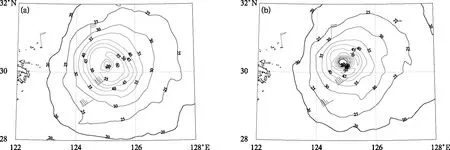
图10 2020年8月24日20时24 h阵风预报及25日20时的小时最大阵风风速观测实况(≥20 m·s-1) (a)ECMWF确定性模式3 h最大阵风预报,(b)基于多元回归方法小时最大阵风预报Fig.10 The 24 h gust forecast at 20:00 BT 24 and the observation (≥20 m·s-1) of the peak gust wind speed at 20:00 BT 25 August 2020 (a) the 3 h maximum gust forecast of ECMWF deterministic model, (b) the 1 h maximum gust forecast by the multiple regression method

通常由台风系统影响造成海上平均风速过大，为进一步验证多元回归阵风方法在台风影响下的可适用性，对比了2016—2019年实况出现较大平均风速时的阵风系数与多元回归方法中平均风速的系数。受大风样本所限，仅对比实况出现20～28 m·s-1平均风时的情况(图11)。如图11所示，多元回归方法中的平均风速系数与实况出现各个量级风速时的阵风系数的中位数均较为接近。因此在台风影响下，即使不考虑近地面层风速切变及低层风速切变的情况，多元回归方法中平均风速项也能够在一定程度上预报出台风影响下的阵风。不同台风的风廓线结构差异明显(廖菲等，2017)，为进一步提高台风影响下阵风预报的准确率，后期需要单独针对台风大风个例进行细致的分析。

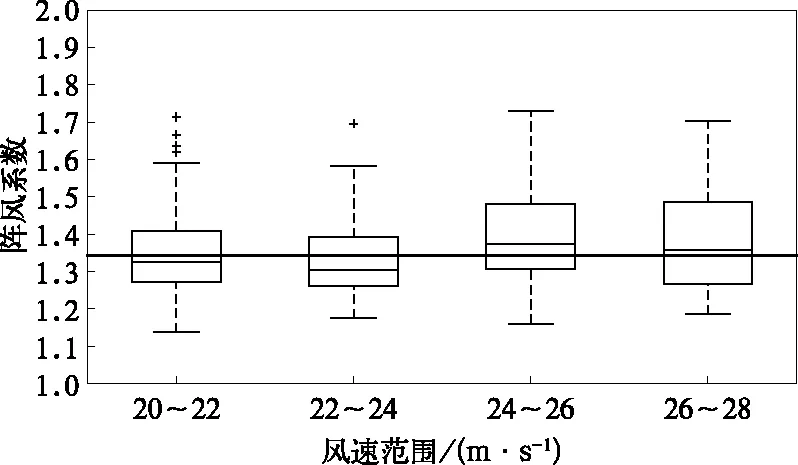
图11 2016—2019年阵风系数箱线图 (粗线：多元回归方法中时刻风速系数为1.343)Fig.11 Box plot of the gust coefficient from 2016 to 2019 (thick line: wind speed coefficient 1.343 in the multiple regression method)

6 结论与讨论

本文基于实况观测数据及再分析数据建立多元回归方法的我国近海逐小时阵风预报方程，并利用2020年ECMWF确定性模式数据进行预报试验，通过对比阵风系数法及ECMWF确定性模式中的阵风预报得出以下结论：

(1)本文的阵风预报方程中包含平均风速项、近地面层湍流作用项以及对流作用项。相比于阵风系数法，基于多元回归方法的阵风预报方程不仅具有统计学意义，同时具有明确的物理意义，因此能够对阵风有更好的拟合效果。

(2)在预报试验中，多元回归方法的阵风预报的平均误差要明显低于阵风系数法。在8～9级阵风预报中，该方法预报效果同样优于ECMWF确定性模式中的阵风预报。

(3)在冷空气大风天气过程中，多元回归方法的阵风预报大风范围明显大于ECMWF确定性模式中的阵风预报，与实况观测更为接近。在台风大风天气过程中，该方法也能够反映出台风影响下的阵风情况。

不同季节、不同平均风速下的阵风情况会有所差异，不同台风影响下的阵风情况也有所不同，但由于实况中大风速样本的数量有限，难以将样本再进行细致划分，因此本文仅建立了一个通用的阵风预报方程。后期可利用更多实况数据，针对不同季节、不同平均风速、考虑不同层结高度建立阵风预报方程，以期取得更好预报效果。相比于ECMWF确定性模式中的阵风预报，本文中所建立阵风预报方程具有更好的适用性，可对不同模式输出数据进行后处理，为海上阵风预报提供更多参考。