基于BP神经网络的武汉市分层水温预报模型研究

陆鹏程 孟翠丽 赵辛慈

（1武汉农业气象试验站，湖北武汉 430040；2武汉市气象局，湖北武汉 430040）

水体温度是水生生物环境中最基本、最重要的因素之一，水温变化不仅直接影响鱼类的生长、繁殖、越冬以及对疾病的抵抗力等，也影响水中溶解氧含量、池塘的物质循环速度等其他外界环境因子。水产繁殖、投饲、起捕、病害发生等全过程均与水温有着十分密切的关系，准确的水温预报对水产养殖生产活动有着重要的指导作用。

关于水温预报的方法，国内外均有一定的研究。Caissie等[1]以气温为变量，使用随机模型和回归模型对Catamaran Brook流域进行了日最高水温模拟，指出随机模型在水温模拟时具有更好的精度，随机模型适用于水温模拟。王 颖等[2]对糯扎渡水库下河道水温的影响因素进行了分析，依据质量守恒方程和一维温度对流扩散方程，建立了一维水温控制方程。李克锋等[3]对流域内河流水温进行实时监测，确定了水温与气温、太阳辐射、湿度等因素之间的相关性，基于最小二乘法原理提出了一个新的水温与气温、湿度和风速等多参量函数表达式。

目前，对水温预报的研究大多从线性关系角度出发，通过建立回归方程开展预报。这样的方法有较强的数据依赖性，预报准确率与数据长度相关，且未考虑气象要素的非线性干扰对水温变化的影响。本文将从非线性角度出发，以机器学习的方式建立基于拟牛顿法的BP神经网络水温预报模型，对水温预报方法进行探究。

1 资料与方法

1.1 资料

本文选用的资料为武汉基本气象观测站2018年12月至2020年11月的气温、气压、风、蒸发、地温、日照等地面观测资料和总辐射、净辐射、直接辐射等辐射观测资料，武汉金银湖湖泊生态观测站2018年12月至2020年11月的分层水温观测资料。

1.2 方法

本文采用相关分析、BP神经网络、BFGS拟牛顿算法，选取与水温密切相关的气象要素，建立基于BP神经网络的武汉市垂向水温预报模型。运用MATLAB软件的神经网络工具箱对模型训练样本的均方误差曲线作图。

1.2.1 BP神经网络。BP神经网络是一种采用误差反向传播算法进行学习的多层前馈型神经网络，目前广泛应用于分类识别、回归、迫近、压缩等领域[4]。其输入信号经隐含层处理至输出层（图1），若输出不满足期望要求，则将误差反向传播并调整网络权值，使输出结果满足期望值。

x1，x2，…，xn是网络输入，y1，y2，…，yn是 BP 神经网络预测输出，wij和wk为网络权值。其隐含层的输出H为：

f函数是隐含层激励函数，为S型函数，其函数表达式为：

BP神经网络的预测输出：

1.2.2 拟牛顿法。20世纪60年代，Broyden提出求解非线性方程组的拟牛顿法（quasi-Newton method）之后，众多研究者对拟牛顿法的局部收敛和全局收敛进行了广泛研究。如今拟牛顿法已成为求解非线性约束、无约束优化问题最有效的方法之一[5]。基于拟牛顿法的改进BP神经网络模型，用一个不包含二阶导数的矩阵近似Hessian矩阵的逆矩阵[6]，通过测量梯度的变化，构造一个目标函数的模型进行迭代，使之足以产生超线性的收敛性。这类方法收敛速度快、误差小、数值稳定，大大优于最速下降法，尤其适用于困难的问题。

2 结果与分析

2.1 影响水温的气象要素选取

建立BP神经网络模型，首先要确定输入层。多项研究表明，水温变化与周边环境的温度（气温、水温、地温）、太阳辐射和风速等气象要素有关[7-9]。其中，温度较为稳定，风速和辐射数据脉动明显。

为得到水温与各气象要素的总体相关系数，本文采用气温、气压、风速和地温的月平均值及蒸发量、日照和辐射的月统计值，分别对 20、40、60、80 cm等层次月平均水温、月极端最高水温和月极端最低水温进行相关分析，并求取4层相关系数平均值如表1所示。可以看出，水温变化与气温、蒸发、相同层次地温、净辐射和总辐射有明显的正相关关系，与气压有明显的反相关关系，与日照和相近层次相关性较弱。

表1 水温月统计值与各气象要素月统计值的相关系数

进一步研究发现，平均、最高、最低水温和平均、最高、最低气温之间的相关性各不相同。图2为2018年12月至2020年11月间各月平均、最高、最低水温和不同气温要素之间的相关系数折线图。从中可以看出，日平均水温与日平均气温的关系密切，日最高水温受日最高气温的影响较为明显，但日最低水温与日平均气温的相关系数大于其与日最低气温的相关系数。上述特征的出现，主要与水温变化的滞后性有关，即受湍流、辐射、传导等热量交换过程影响而出现的水温变化明显滞后于气温。

2.2 模型与仿真

基于BP神经网络，通过拟牛顿法对水温进行建模，并利用MATLAB对各季节各层水温预报开展仿真试验。为提高水温模型预报性能，参考气温预报评分方法，定义预报值与实际值的绝对误差小于2℃即为正确，根据测试样本准确率、均方误差（MSE）、均方根误差（RMSE）及平均绝对误差（MAE），分析水温模型预报性能。

2.2.1 模型设计。不同水温要素、不同层次和各季节水温的变化规律各不相同。为降低模型复杂度，分季节、要素对垂向多层水温进行模拟，即针对不同季节、不同要素分别建立模型，将 20、40、60、80 cm 等4层水温作为输出。

经前文研究发现，水温变化与气温、气压、蒸发、地温、日照和辐射等气象要素密切相关，结合日常业务经验和试验，确定输入层维数为1，以前一天的气象要素和水温作为输入，其中具体输入的气象要素如表2所示。

表2 平均、最高、最低水温模型输入的气象要素

2.2.2 训练方法。本文分季节对2年的逐日数据样本进行随机选取，采用串行方式进行训练，通过BFGS拟牛顿法对模型进行快速收敛，以提高速度和增强样本随机性，避免陷入局部最优。

2.2.3 参数设置。对于隐含层神经元个数、学习精度和最大失败次数等参数的确定，目前缺乏有效的方法[10]。经过多次试验，确定QN-BP神经网络模型总体参数如下：训练参数为trainbfg，隐含层数为1，最大训练次数为5 000，学习精度为10-6，学习率为0.01，最大失败次数为20，一维线性搜索方法为srchcha，训练样本数为120。隐含层节点数具体如表3所示。

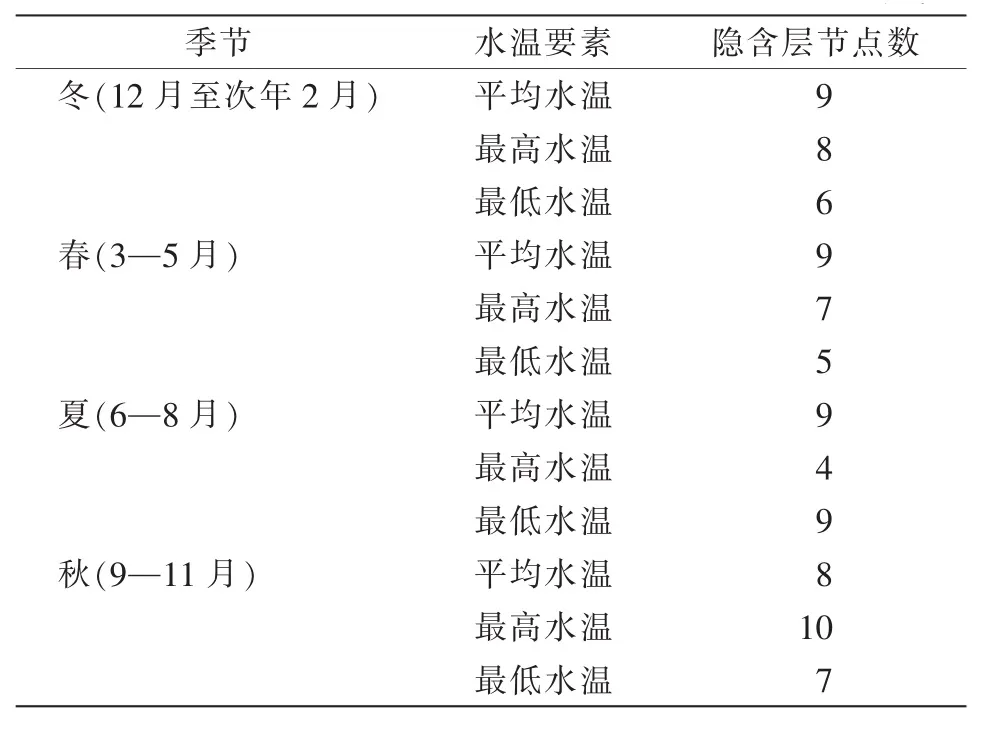
表3 各季节平均、最高、最低水温预报模型隐含层节点数 单位：个

2.2.4 仿真结果。基于拟牛顿法BP神经网络原理，采用前文所述的训练方法分季节建立垂向分层水温预报模型。通过多次学习试验，优化训练参数，测试水温预报模型性能，并对训练和测试样本进行分析。图3、4、5分别为各季节平均、最高、最低水温预报模型训练样本的均方误差曲线。对于测试样本而言，平均、最高、最低的水温预报模型在各季节均能快速收敛且满足预期，但秋季的平均水温和春、夏季最高水温的均方误差相对较高。

为验证水温模型预报性能，统计各季节平均、最高和最低水温预报模型测试样本的均方误差、均方根误差和平均绝对误差及预报准确率，如表4、5所示。从中可以看出，水温模型性能稳定、准确率高，其平均预报准确率高达91.2%，平均绝对误差小于1℃。从水温预报准确率角度分析可知：最高水温的预报准确率明显低于平均水温和最低水温，平均水温和最低水温的平均预报准确率超过95%；浅层水温的预报准确率低于深层水温；春季的预报准确率略低于其他季节。分析误差可以明显看出，最高水温的预报误差2倍于平均水温、最低水温，春秋季预报误差略高于冬夏季节。

表4 水温模型测试样本均方误差、均方根误差和平均绝对误差

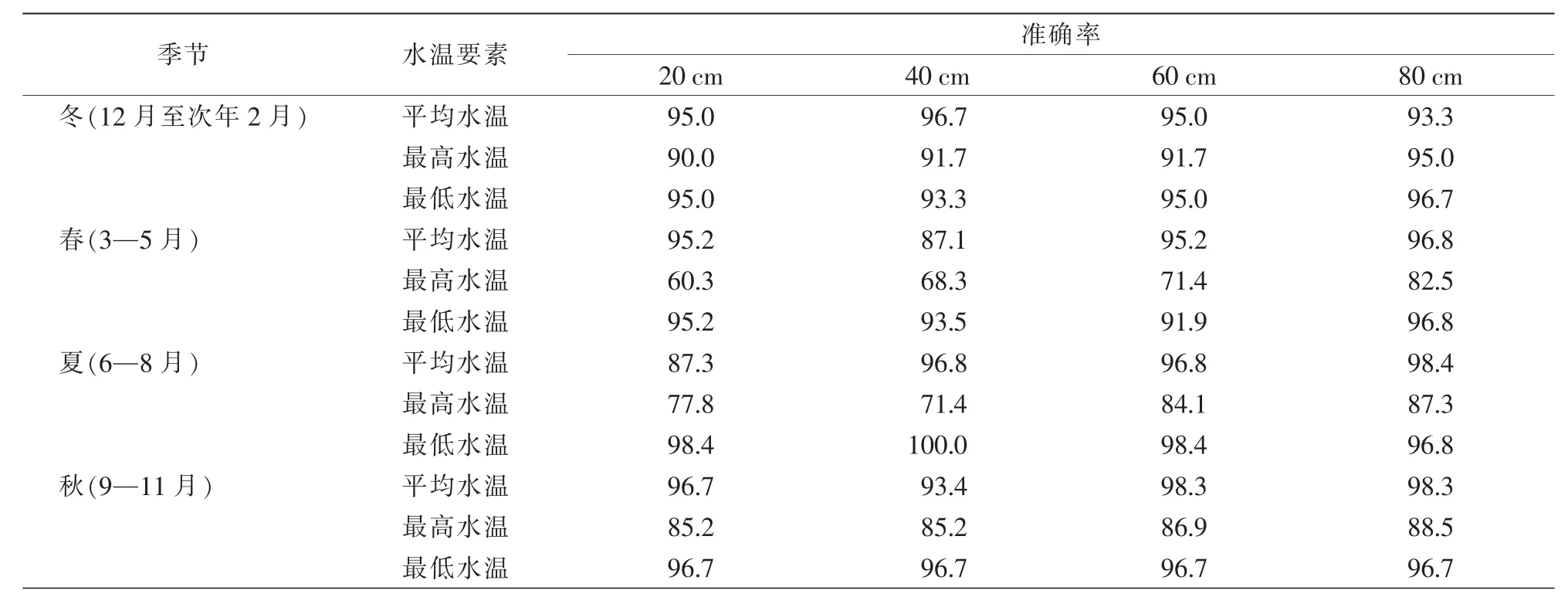
表5 水温模型各层预报准确率 单位：%

3 结论

研究结果表明，水温的变化与气温、蒸发、气压、邻近地温、日照和辐射等气象要素的相关关系明显，通过气象要素能够对水温进行预报。基于拟牛顿法的BP神经网络水温预报模型具有收敛速度快、误差较小、数值稳定等特点，平均绝对误差小于1℃，水温预报的平均准确率高达91.2%，平均水温和最低水温的平均预报准确率甚至超过95%。相对于其他要素，日最高水温敏感性较高，更易受预报当天气象条件的影响，其预报准确率明显低于平均和最低水温；同理，浅层水温的预报准确率低于深层水温。同时，春秋季节气候多变，水温预报难度略高于冬夏。

[6]刘天舒.BP神经网络的改进研究及应用[D].哈尔滨：东北农业大学，2011.

[7]欧阳潇然，赵巧华，魏瀛珠.基于FVCOM的太湖梅梁湾夏季水温、溶解氧模拟及其影响机制初探[J].湖泊科学，2013，25（4）：478-488.

[8]赵林林，朱广伟，陈元芳，等.太湖水体水温垂向分层特征及其影响因素[J].水科学进展，2011，22（6）：844-850.

[9]甘衍军，李兰，武见，等.基于EFDC的二滩水库水温模拟及水温分层影响研究[J].长江流域资源与环境，2013，22（4）：476-485.

[10]刘冰.MATLAB神经网络超级学习手册[M].北京：人民邮电出版社，2014.