基于HyperMesh二次开发的复合材料机翼结构优化设计

桂天才，杨 文，程家林

(航空工业成都飞机工业(集团)有限责任公司，四川 成都 610091)

0 引 言

研究表明，复合材料因具有轻质、高比强度、高比刚度以及可设计等优点，而被广泛应用于飞机机翼的结构设计之中[1].通常，飞机机翼结构一般布置有梁、肋、蒙皮及长桁等构件.其中，前梁一般布置于占翼弦长的15%左右处，后梁一般位于翼弦长的55%～60%处，且前后梁布置需要与前后缘舵面布置及起落架的布置相协调.翼肋的布置形式主要采用顺气流航向布置、垂直于前梁或后梁轴线正交布置以及两者的混合布置等方式.

飞机机翼结构优化设计也是飞机设计的关键技术之一，通过优化设计，不仅可以减轻飞机机翼结构的质量，还能够显著提高飞机性能.研究表明，复合材料翼面结构综合优化设计技术可以充分发挥复合材料可设计性的优点,利用复合材料铺层的方向性、可设计性，以及具有设计空间大、易于整体成形的良好工艺性等特点，可以实现结构设计在效率、性能、功能和成本的综合优化[2].事实上，飞机的复合材料结构设计需要综合考虑强度、刚度及稳定性等多种约束，其优化设计问题是一个设计空间大、约束条件多与情况复杂的系统工程.针对复合材料翼面结构设计优化的相关问题，科研人员已做了大量的工作.例如，邓扬晨等[3]与赵群[4]分别采用分级优化策略完成了复合材料翼面结构优化设计；王宇等[5]采用刚度等效方法来减少设计变量，完成了复合材料机翼结构的优化；柯志强等[6]综合考虑多种约束，完成了飞机机翼结构的优化设计；Jin等[7]采用改进的遗传算法完成了大展弦比复合材料机翼结构的优化设计；朱振涛[8]和韩伟等[9]分别采用多学科优化软件isight集成nastran完成了复合材料机翼结构的优化.此外，丁燕等[10]基于HyperMesh二次开发完成了机身结构尺寸快速设计平台的开发；刘剑霄等[11]基于HyperMesh二次开发完成了飞行器尾翼复合材料结构建模和优化分析，极大地提高了设计效率.

相关研究与工程应用表明，HyperMesh二次开发语言TCL(Tool Command Language，TCL)类似于C语言，可以高效快速地完成多变量与多约束结构的优化模型的建立.基于此，本研究拟采用HyperMesh二次开发语言TCL完成复合材料机翼结构的优化模型建立，并通过使用循环语句，批量创建结构属性、设计变量与约束条件等，快速得到优化模型和优化结果，从而提高飞机机翼结构优化设计的工作效率，并实现减轻机翼结构质量的目的.

1 有限元模型的建立

1.1 机翼结构外载荷

通常，在飞机的飞行任务剖面内，包含有多种载荷工况，在对其进行结构设计时，需要确保飞机在各种飞行工况下的结构强度要求.现代飞机结构设计通常需要从飞行包线中挑选出典型的危险载荷，然后再进行飞机的结构设计.

飞机机翼的载荷主要包括上下翼面气动压力，翼盒内部燃油和结构本身的质量，以及发动机挂架对机翼的集中载荷.对此，本研究采用了2个简化假设：第一，不考虑机翼上的集中载荷；第二，认为整机升力均由机翼产生.基于此假设，本研究分别沿机翼展向与机翼弦向做了约定，具体如图1所示，即机翼载荷展向为椭圆分布，且机翼载荷沿弦向为均匀分布.

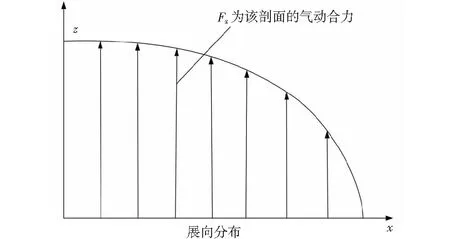
图1 飞机展向的载荷分布假设示意图

由于飞机一般有2个机翼且载荷分布为椭圆分布，故单个机翼的载荷Pmax0应满足，

(1)

其椭圆载荷的表达式为，

(2)

假设载荷沿着弦向均匀分布，则可获得机翼蒙皮表面的气动载荷分布为，

(3)

通常，飞机的设计载荷为飞机的最大起飞质量与设计过载及安全系数的乘积.在本研究中，给定的设计过载为，nd=-1 g～2.5 g，结合结构设计中给出的安全系数(f)与最大起飞质量(wto)，则可计算得出机翼的设计载荷Pd,max和Pd,min,进而通过式(3)可确定机翼的气动载荷分布.本研究中，气动载荷可以场函数的形式加载在机翼下蒙皮上.

1.2 机翼结构有限元模型

按照工程经验和使用要求，本研究利用Catia完成机翼结构几何模型的建立，具体方案为：半翼展5 000 mm，根弦长1 600 mm，翼尖弦长560 mm;前梁布置在30%位置，后梁布置在70%位置;翼肋布置为等间距分布，距离为1 000 mm；按照上蒙皮、下蒙皮、翼梁与翼肋建立4个分组，以便于导入HyperMesh中进行网格的划分.机翼的梁、肋布置情况如图2所示.在此基础上，使用HyperMesh划分网格，并建立分组，完成后，机翼结构的有限元模型如图3所示.

图2 机翼结构的布置情况

图3 机翼结构的有限元模型

本研究中，使用TCL函数赋予属性，其中，梁、蒙皮和肋腹板为PSHELL单元，梁肋缘条使用PROD单元，每个梁肋之间的格子里的单元为一个属性.设定机翼根部和外翼段前后梁的节点位移约束为固支.参考Crood 1来定义上、下壁板的载荷场函数，然后通过载荷模块中的CID distributed load将压力场函数施加在下蒙皮上.其中，梁与肋缘条使用PROD单元，假定其铺层比例为6∶3∶1，弹性模量采用等效模量计算.据此，可以得到1d单元的等效模量为，Ex=7.40×104MPa,Gxy=1.13×104MPa.机翼结构材料的具体参数如表1所示.

表1 T700材料参数表

2 复合材料机翼结构优化模型

2.1 机翼结构优化设计模型

在机翼结构优化模型中，本研究以其质量最轻为目标函数，以各分区按0 °、±45 °、90 °铺层厚度及梁元面积为设计变量，并综合考虑静强度、静刚度和稳定性等约束条件，且每种角度的铺层比例不少于10%，并通过优化设计得到按0 °、±45 °、90 °方式的4种铺层厚度.其优化设计模型为，

minM(X)

(4)

2.2 设计变量建立

目前，在复合材料的结构设计中，一般采用0 °、±45 °、90 ° 4种铺层角度，并设计成对称均衡形式，即，t45°=t-45°,且任意形式的目标复合材料层合板可以等效为仅包含4种角度的辅助层合板，其具体结构如图4所示，即可以将相同铺层角度的铺层放在一起.这样做可以仅设计各分层的铺层厚度，降低了设计变量的数目，进而提高了优化效率.

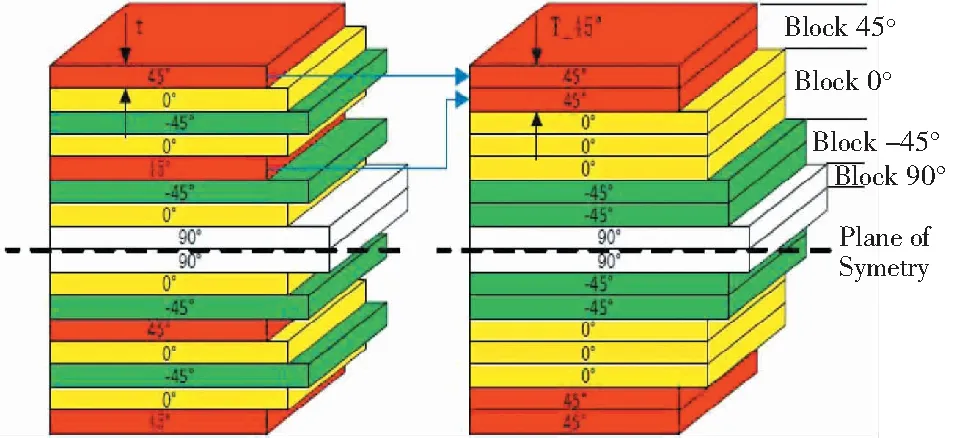
图4 辅助层合板设计示意图

本研究在优化设计时，不直接建立加筋板筋条，而是采用“打扁”的方式来建立加筋板，并将加筋板全部建成壳元PSHELL.对于每一个PSHELL属性，其包含3个变量，ps$i-t0、ps$i-t45与ps$i-t90.使用TCL批量建立设计变量，总共属性有55个，建立的厚度设计变量有165个.利用for循环批量建立设计变量，其部分代码如下：

set number_of_surfs 55；

for {set i 1} {$i <=$number_of_surfs} {incr i}

{

*createmark designvars 2

*clearmark designvars 2

*sizedesvarcreatewithddvalfield "ps$i-t3" 6 2 0.15-1 0

*createmark designvars 2

*clearmark designvars 2

*createmark designvars 2 "ps$i-t3"

*clearmark designvars 2

*createmark designvars 2

*clearmark designvars 2

*sizedesvarcreatewithddvalfield "ps$i-t2" 6 2 0.15-1 0

*createmark designvars 2

*clearmark designvars 2

*createmark designvars 2 "ps$i-t2"

}

同时，对于prod每个属性定义一个设计变量，即，对于每个prod属性以截面面积为设计变量，并使用prod opti批量建立1d单元设计变量.其中，prod单元的数目有62个，故建立62个变量.

2.3 约束条件建立

2.3.1 尺寸约束

尺寸约束也称为设计变量的上、下边界约束.在本研究中，各元件设计变量的尺寸约束定义为：每一个铺层角度的厚度变量∈[0.15 mm，6 mm]，初始值为2 mm；一个prod截面面积变量∈[1.13 mm2，300 mm2]，初始值为38 mm2.

2.3.2 2d-复材铺层百分比约束

通常，在优化设计中，每个铺向角的铺层比例yid 不少于10%，而对于螺栓连接区域，其±45 °的铺层至少达40%，以避免发生挤压损坏.对此，本研究对每一个pcomp属性的铺层中的0 °、±45 °、90 °的铺层百分比进行约束，各个角度的铺层百分比为：0 °铺层比例约束为[0.2，0.5]；±45 °铺层比例约束为[0.4，0.7]；90 °铺层比例约束为[0.1，0.4].

以上约束通过TCL批量创建，由于有55个pcomp属性，所以需要创建165个响应和约束.对此，本研究创建了3个function，用于定义每个属性ps1的铺层百分比perc1、perc2与perc3，每个ps$i有3个百分比响应，并与各自的方向角度厚度变量关联，然后对每个铺层百分比约束，其部分代码如下：

for {set i 1} {$i <= $number_of_surfs} {incr i}

{

*createarray 3 $did3 $did2 $did1

*optiresponsesetequationdata1 "resp-perc-ps$i-1"

3 0 0 0 1 3

*optiresponsesetequationdata2 "resp-perc-ps$i-1"

0 0 1 0

}

2.3.3 2d-复合材料应变约束

本研究首先创建复合材料的应变响应，包括拉伸应变、压缩应变与剪切应变，然后对各个应变进行约束.相关约束条件为：最大拉伸应变为，con-2d-maxp ∈[-5 500 με, 5 500 με]；最小压缩应变为，con-2d-minp∈[-4 000 με, 4 000 με]；最大剪切应变为，con-2d-shear∈[-3 800 με, 3 800 με].

2.3.4 1d-轴向应力约束

根据，σ=Eε，可以得到等效杆元的应力约束为:-300 MPa≤[σ]≤400 MPa.

2.3.5 稳定性约束

在各工况下，本研究对于受压剪载荷作用的结构元件，如上壁板与梁腹板，不允许出现结构失稳，且机翼不出现整体失稳，并留出一定裕度.故，设定屈曲因子，λ≥1.2.

2.3.6 翼尖变形约束

本研究对翼尖的位移约束主要是限制机翼在气动力作用下沿垂直翼面方向的弯曲变形.若机翼沿垂向的变形较大，虽在一定程度上可增加飞机的横向稳定性和操纵性，但也会恶化机翼表面的气动力状况并降低飞机升力，故必须对机翼垂向弯曲变形加以约束.在一般的机翼结构优化过程中,通常设定机翼翼尖位移≤ 10 %机翼半展长.同时，由于机翼的压心和刚心位置不重合，导致其在气动载荷作用下会产生较大的扭转变形，使得机翼的空气动力特性变差.因此，机翼设计时应保证足够的扭转刚度，即翼尖扭转变形应不超过给定值，通常设定机翼翼尖扭转角控制在-3 °～1 °之间(机翼前缘抬头为正).

据此，本研究的翼尖变形约束为：翼尖最大变形∈[-500 mm, 500 mm]；翼尖扭转变形，∈[-3 °, 1 °].

2.3.7 目标函数建立

本研究的优化模型以机翼结构质量最轻为目标函数.

3 优化结果

根据机翼结构初始参数，本研究使用HyperMesh建立复合材料机翼结构有限元模型，使用HyperMesh二次开发语言TCL批量建立属性，然后提交optistruct分析，机翼结构的初始的质量为191.7kg，模型的初始响应结果如图5所示.

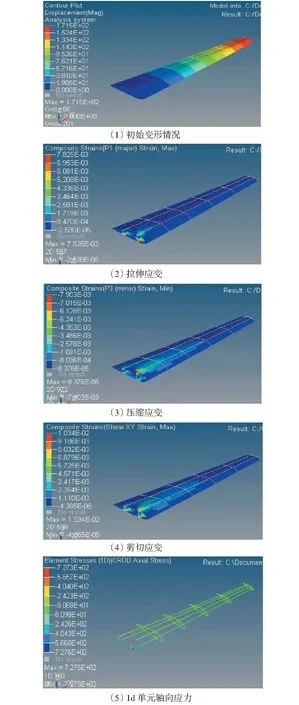
图5 初始模型的响应结果

同时，使用基于HyperMesh二次开发的方法建立复合材料机翼结构优化模型，其中，设计变量数目227个、优化响应174个、自定义函数67个、约束条件171个.通过提交optistruct优化，经过31次迭代，模型实现收敛并获得优化前后的约束响应，具体结果如表2所示.优化后的机翼蒙皮厚度分布如图6所示，优化模型响应结果如图7所示.

图7 机翼结构优化模型的响应结果

表2 优化前后结果对比

图6 优化前后机翼蒙皮厚度对比

对比上述图表可知，通过建立模型对飞机机翼结构进行优化，机翼结构质量由最初的191.7 kg降低至159.9 kg，减少了16.6%，并且所有约束条件优化后值均满足约束要求.优化结果表明了本优化模型的正确性和有效性.

4 结 论

本研究基于HyperMesh二次开发建立了飞机复合材料机翼结构多变量与多约束的优化模型，并使用二次开发语言TCL批量创建了属性117个、设计变量227个、自定义函数67个、约束响应174个与约束条件171个，提高了机翼结构优化设计的工作效率.通过optistruct对本研究所建机翼结构模型进行优化，机翼结构质量减轻了16.6%，表明了本优化模型的正确性和有效性.本研究结果可应用于相关结构的优化模型的快速建立，此对于结构的方案设计与快速评估具有实际的参考价值