基于GA-QPSO算法的含分布式电源配电网优化重构设计
2022-04-06陈奎,潘磊
陈 奎, 潘 磊
(中国矿业大学电气与动力工程学院,江苏徐州 221000)
0 引 言
近年来,由于传统能源储量不断减少,用电需求不断增加,凭借污染少、可持续再生等多种优势的新能源发电技术逐渐成为当前研究的热门方向,该技术也对我国实现能源结构转型具有重要的促进意义[1]。分布式电源具有较强的波动性和随机性,并网后,势必会对电网的结构、供电方式和潮流方向产生影响,对电力系统的运维技术、电能质量、可靠性、安全性以及节能性发起了挑战。在现有的电网条件下,如何寻求到一种更合理的运行结构,成为国内外诸多学者的重要研究方向。
从数学角度来看,配网重构属于一种多约束、多目标的组合优化问题,随着配电网规模不断扩增,重构技术涉及的线路开关组合数量变得十分庞大,导致许多传统的数学方法和启发式算法不再适用[2]。近年来,由于智能优化算法不断被改进,许多学者对基于智能优化算法的重构技术进行了大量研究。文献[3]中提出一种改进的蚁狮搜索算法,并在初始化种群时引入混沌搜索,提高了算法的全局搜索能力,但寻优速度并未得到有效改善。文献[4]中提出了一种基于量子粒子群和引力搜索混合算法,结合改进的前推回代潮流计算方法,使得整体寻优性能有所提升,该算法并未考虑含分布式电源的配网重构。文献[5]中提出一种基于改进蚁群算法的配电网重构算法,结合图论算法对迭代过程中的解进行筛选,极大提高了寻优效率。文献[6]中依托传统粒子群算法,将配电网最大传输能力作为寻优目标函数,并结合环路搜索法排除不合理的解,大大降低了搜索时间。以上研究不仅为智能搜索算法在配电网重构应用提供了许多新思路,也为后续研究奠定了重要的理论基础。
基于以上启发,本文将遗传算法(Genetic Algorithm,GA)的种群更新方式引入到量子粒子群算法(Quantum Particle Swarm Optimization,QPSO),提出一种改进的GA-QPSO算法。通过结合GA和QPSO两种算法的优势,在迭代过程中改善种群多样性不足和收敛性不强等问题,以IEEE33节点配网系统作为算例,验证该算法的有效性。
1 重构模型
1.1 优化目标
配电网重构就是通过改变线路分段开关和联络开关的组合方式,以实现对电网结构的改变,达到优化电网的各项指标。目标函数通常分为配电网的功率损耗最低、节点电压偏差最低、消除过载、均衡负荷等[7]。针对含有大量分布式电源接入的情况,本文以有功损耗最低为目标函数[8]:
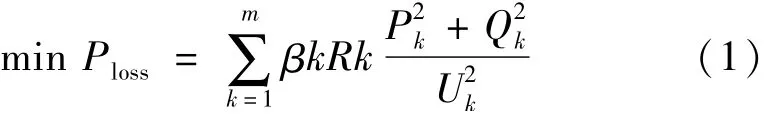
式中:m为配电网中的支路总数;βk为该支路上联络开关或者分段开关的开合状态,闭合时值为1,断开时值为0;Rk为支路k的电阻值;Pk、Qk分别为支路k的有功和无功功率;Uk为支路k末端电压。
1.2 约束条件
含分布式电源配网系统进行优化重构时,除了考虑优化目标外,还须考虑重构后的系统是否满足规定的运行条件。
(1)潮流约束[9]
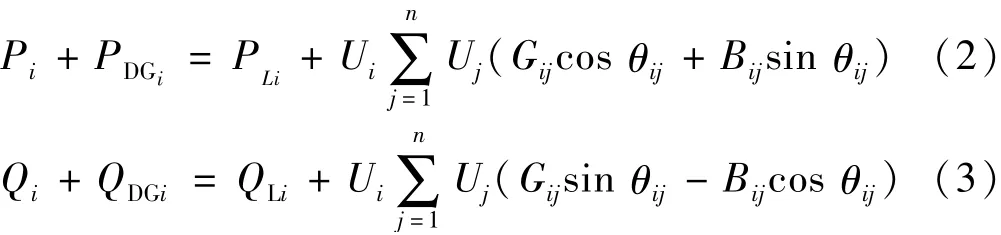
式中:Pi、Qi分别为节点i处系统注入的有功功率和无功功率;PDGi,QDGi分别为DG接入节点i处注入的有功功率和无功功率;PLi,QLi分别为节点i负荷的有功功率和无功功率;Ui,Uj分别为节点i和j的电压有效值;Gij为节点导纳矩阵实部;Bij为节点导纳矩阵虚部;θij为节点i和节点j的电压相角差。
(2)节点电压约束[10]
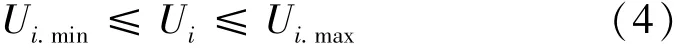
式中:Ui为节点i的电压;Ui.min和Ui.max分别为节点i电压下限和上限。
(3)支路容量约束[11]

式中:Pk、Qk分别为流过支路k的有功和无功功率;Sk.max为支路k的传输容量上限。
(4)拓扑结构约束

式中:hk为重构后的电网结构;Hk为符合电网运行规则的网络结构。配电网重构后要保持辐射状结构,不能出现环路或孤岛。
2 重构算法
2.1 量子粒子群算法
传统的粒子群算法(Particle Swarm Optimization,PSO)是通过更新粒子的速度和位置来实现粒子更新迭代,正是因为这种以轨道的形式来实现收敛的方式,使得粒子每一次迭代步的搜索空间非常有限,极易陷入局部最优解[12]。基于此,孙俊[13]在传统PSO算法的基础上提出了QPSO算法,其迭代公式:
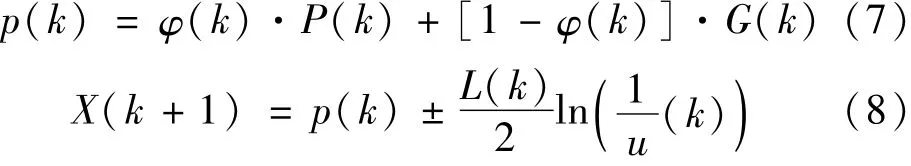
式中:p(k)为第k次迭代时粒子的吸引子坐标;φ(k)为区间(0,1)上均匀分布的随机数;P(k)、G(k)分别为个体最优粒子和全局最优粒子;X(k+1)为第k+1次迭代时的粒子位置;L(k)为势阱特征长度,随迭代次数增加而减小直至趋近于0;u(k)为区间(0,1)上均匀分布的随机数。
由式(7)、(8)可见,QPSO算法不再依托速度和位置来更新粒子,而是利用距离和位置来更新粒子。其中吸引子位置由全局最优解和局部最优解共同决定,粒子第k+1次迭代时的位置随机出现在吸引子附近。迭代末期,随着L不断趋向0,粒子最终将跌落到吸引子位置,达到收敛的目的,这也就克服了传统PSO算法寻优过程中种群基因多样性不足、易于陷入局部最优的缺点。
2.2 改进的量子粒子群算法
QPSO算法比PSO算法具备更优良的搜索和收敛能力,在处理配电网重构问题时,仍然存在许多困难。由于配电网结构需要满足许多约束条件,在搜索过程中会出现大量不合理的解,极大影响搜索速度。在配网重构中对线路开关状态的编码通常以0和1表示,配网重构模型属于二进制寻优模型,该模型对于距离的定义与连续域存在很大的差异。针对以上两个问题,本文引入了GA中“遗传”和“变异”的思想,吸引子p(k)的位置将依概率遗传个体最优解P(k)和全局最优解G(k)的优良基因,同时非优良基因将依概率发生变异,因此其迭代方式为:
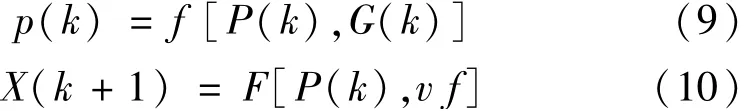
式(9)为遗传操作;式(10)为变异操作;v f为变异因子。在搜索前期为了使粒子更具有多样性,覆盖更广泛的搜索空间,变异因子应取较大值;在搜索末期,为加快粒子聚集和收敛,变异因子应取较小值。本文借鉴了标准PSO算法中惯性权重的迭代递减策略,使v f的取值为[14]:
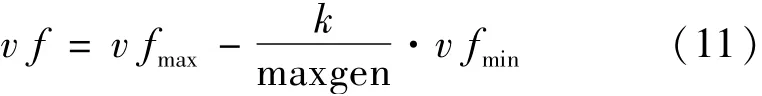
式中:k为迭代的当前次数;maxgen为最大迭代次数;v fmax为变异因子最大值;v fmin为变异因子最小值。
在搜索中后期,由于粒子群已经开始呈现聚集态,对粒子以轮盘赌的方式实行自我交叉操作,遵循相邻基因交叉概率大于非相邻基因交叉概率原则,实现局部深度搜索,提高算法收敛于全局最优解的能力。
GA-QPSO算法具体流程如图1所示。
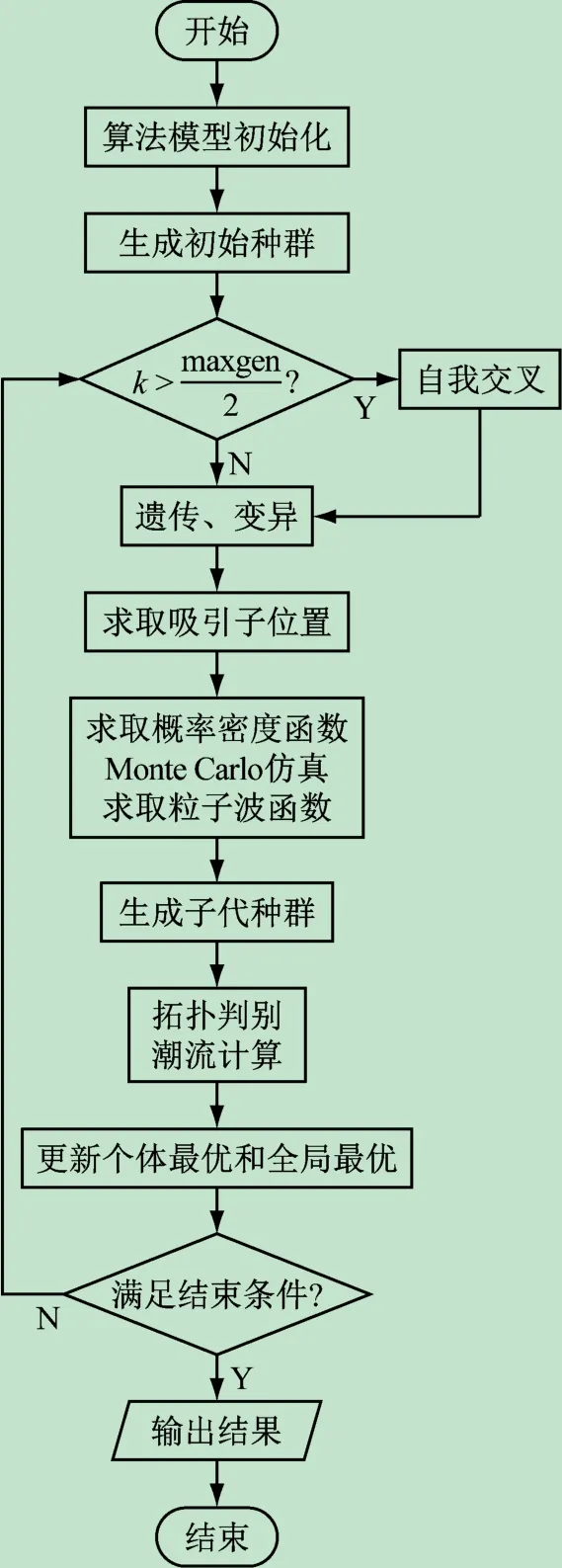
图1 基于GA-QPSO算法配电网优化重构流程图
3 算例分析
为验证GA-QPSO算法应用于配电网优化重构时的各项性能,以标准IEEE33节点配网系统为例,通过Matlab进行仿真分析。IEEE33节点配网系统原始拓扑结构如图2所示,其中包含33个节点、32个分段开关(均闭合)、5个联络开关(均断开),系统基准电压为12.66 kV,有功负荷为3.715 MW,无功负荷为2.3 Mvar,基准容量设置为10 MVA。GA-QPSO算法种群规模为10,最大迭代次数为40,最大变异概率v fmax为0.9,最小变异概率v fmin为0.4。

图2 标准IEEE33节点系统原始拓扑结构图
3.1 不含分布式电源的优化重构分析
表1为几种智能算法针对不含DG的IEEE33节点配网系统优化重构的最终搜索结果,图3为几种智能搜索算法的收敛特性曲线,图4为重构前后各节点电压对比图。

表1 不含DG的IEEE33节点重构数据
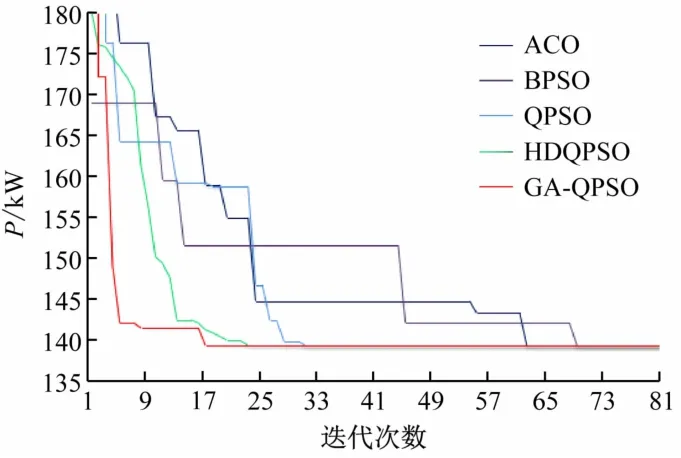
图3 不含DG的IEEE33节点系统优化重构收敛特性曲线
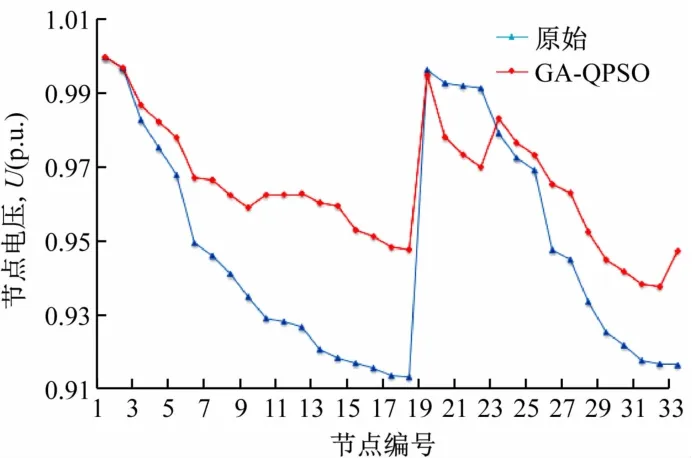
图4 不含DG的IEEE33节点系统优化重构后节点电压
由表1数据可见,各算法最终都能搜寻到全局最优解,断开支路组合均为[7 9 14 32 37],网络有功损耗从202.63 kW降低到139.47 kW,降损率达到31.17%,由图4可见,各节点电压也得到明显提高。
通过比较图3中各算法收敛特性曲线来看,二进制粒子群算法在迭代71次后收敛,蚁群算法在迭代63次后收敛,经典量子粒子群算法在迭代30次后收敛,文献[15]中所提出的HDQPSO算法在迭代22次后达到收敛,GA-QPSO算法在17次迭代后便完成收敛,寻优速度更快。
3.2 同种类型(PQ)分布式电源并网的优化重构
为验证本文所提出的算法是否适用于含同种类型DG的配电网优化重构,参考文献[16]中在IEEE33节点系统中加入4个PQ型分布式电源,相关并网参数见表2,收敛特性曲线如图5所示,相关重构后的数据如表3和图6所示。
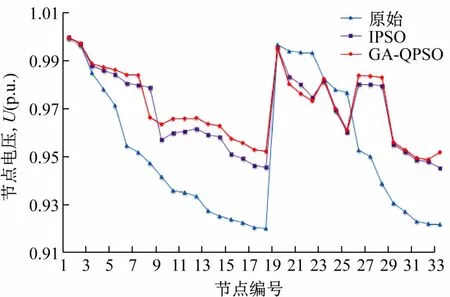
图6 含PQ型DG的IEEE33节点系统优化重构后节点电压
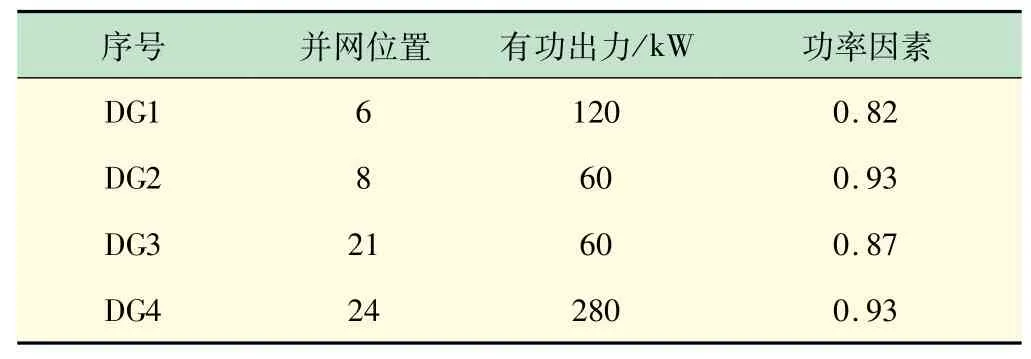
表2 PQ型DG并网参数
由表3可见,文献[18]中所提出改进PSO算法经过17次迭代寻优后得出的断开支路组合为[8 14 28 32 33],有功损耗由原来的165.65 kW降低到109.59 kW,降损率为33.84%。GA-QPSO算法经过10次迭代寻优后得出的断开支路组合为[7 9 14 28 32],有功损耗仅为105.78 kW,降损率为36.14%。通过对比图5中各节点电压值可以看出,经过两种算法优化重构后,各节点电压均有明显提升,但整体而言,GA-QPSO算法寻优结果更接近全局最优。

表3 含PQ型DG的IEEE33节点重构数据
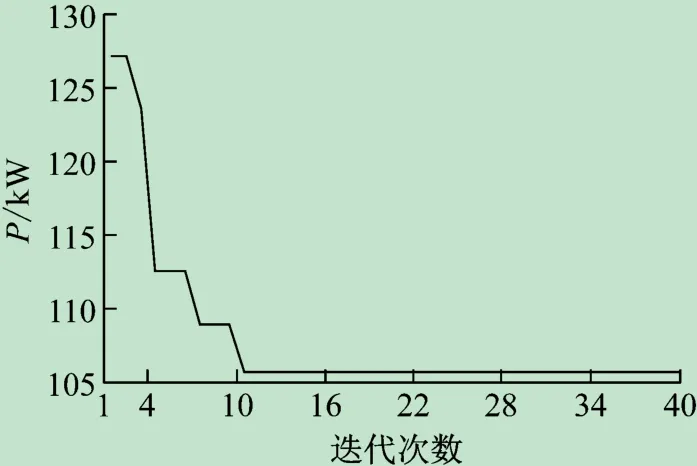
图5 含PQ型DG的IEEE33节点系统优化重构收敛特性曲线
3.3 多种类型分布式电源并网的优化重构
分布式电源类型繁多,并网技术也有所不同,除了PQ节点类型外,还有PV、PI等其他节点类型。为验证本文所提出的算法是否适用于含多种节点类型的分布式电源配电网优化重构,参考文献[17]中在IEEE33节点系统中引入PQ、PI和PV型DG,具体并网参数见表4,收敛特性曲线如图7所示,相关重构后的数据如表5和图8所示。

表4 PQ、PI、PV型DG并网参数

表5 含PQ、PI、PV型DG的IEEE33节点重构数据
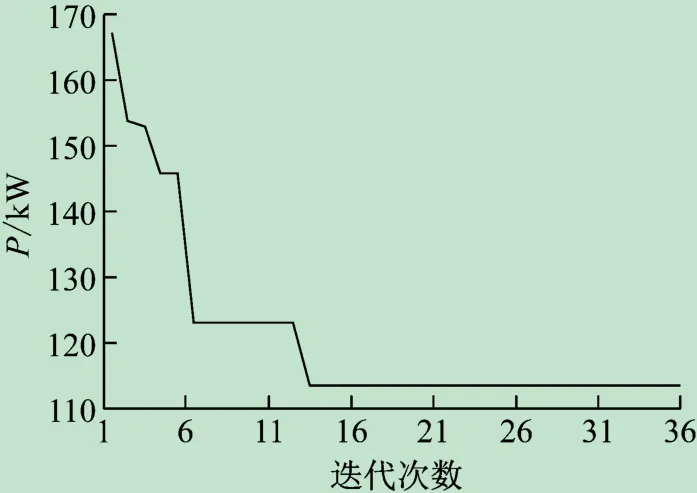
图7 含PQ、PI、PV型DG的IEEE33节点系统优化重构收敛特性曲线

图8 含PQ、PI、PV型DG的IEEE33节点系统优化重构后节点电压
由重构后的数据可见,加入DG后的原始网络节点电压有了大幅提升,但有功损耗却并未得到改善。采用本文所提算法进行重构后,有功损耗由204.12 kW降低到113.55 kW,降损率达到44.37%,节点电压也较不含DG的原始网络有很大提升。从算法收敛特性曲线来看,当迭代次数达到13次时,便收敛到全局最优,说明GA-QPSO算法在处理含有不同类型DG的配电网优化重构问题时具有较快的收敛速度。
4 结 语
本文针对含分布式电源配电网优化重构问题,设计了一种结合GA和QPSO的组合优化算法。该算法通过改进种群的更新方式,有效规避了迭代时易于陷入局部最优而出现“早熟”的状况,大大提高了寻优速度和全局收敛能力。通过对不含分布式电源、含同种分布式电源以及含多种分布式电源的配电网优化重构问题进行仿真分析,结果表明,GA-QPSO算法都能在较少迭代次数内有效搜寻到最佳网络结构,大大降低网络损耗,提高网络节点电压。本文的研究仅针对含分布式电源配电网的静态重构,并未考虑不同时间段内负荷波动以及分布式电源出力波动的影响,接下来的研究工作将重点针对配电网动态重构展开。
