基于振动特征的数控转台可靠性分析实验

王丽丹， 郑 雨， 陶桂宝

（重庆大学机械与运载工程学院，重庆 400030）

0 引 言

机械制造行业作为我国的主导产业，是向强国发展的“助推器”［1-2］。伴随着工业化进程的不断推进，制造业越发的生机蓬勃，而数控机床则是为其发展提供驱动力的重要工具。作为数控机床中最重要的运动轴，数控转台的性能直接决定了数控机床的加工质量。国产数控转台可靠性较低是制约国产机床发展的重要因素。因此，对于数控转台的研究还需投入相当程度的重视和支持［3-4］。

随着机械设备向着高精密、智能化方向发展，其性能上的差异主要体现在可靠性方面。可靠性技术贯穿设备的设计、制造和使用3个阶段，是决定设备质量的重要因素［5-6］，其中设备在运行过程中的可靠度更是可靠性工程中的重点研究对象，因此有必要对设备可靠性评估方法进行研究。传统可靠性分析方法基于大量样本的数据统计，确定可靠性分布函数，求取一批设备的平均可靠度。然而，每台设备随着工作条件的不同，其故障和失效情况都不同，因此基于大样本的可靠性评估方法不适用于单个设备的分析［7］。

为了弥补传统分析方法的不足，国内外学者进行了深入研究，提出了一系列新的可靠性评估方法［8-11］：Huang等［12］针对设备早期故障和后期故障数据之间的差异性，提出了基于惩罚似然函数和最大期望函数的混合模型估计方法，并通过实验数据验证了该方法的有效性。张根保等［13］针对零件加工过程的任务情况，提出根据任务分配可靠性的方法，并利用模糊集理论定义了确定隶属度的模糊真值函数。Xu等［14］结合在线故障预测算法，提出了一种新的动态系统实时可靠性预测方法。

本文以国产TK13系列数控转台为研究对象，建立了基于转台振动特征的威布尔比例故障率模型，用于转台的实时可靠度评估。弥补了传统可靠性分析方法基于历史故障数据做分析无法得到设备实时可靠度的不足，对改善数控转台的使用，提升数控转台可靠性具有参考价值。

1 数控转台振动可靠性分析

1.1 基于振动特征的威布尔比例故障率模型

比例故障率模型（Proportional Hazards Model，PHM）是一种能将设备运行状态与失效率函数结合分析的可靠性分析模型［15］。通过建立设备多个运行状态特征值与可靠性之间的数学模型，即可根据当前设备的实时运行特征量评估设备的可靠性。模型如下：

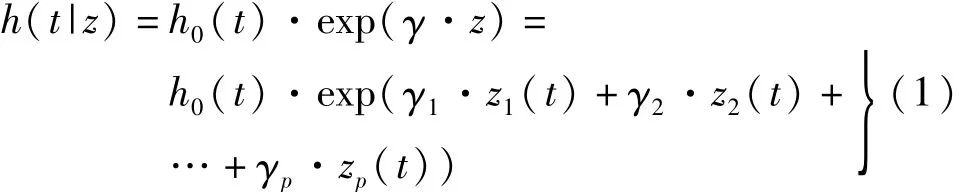
式中：h0（t）表示基准风险函数；z表示协变量，本文试验的振动特征向量；γ表示协变量的回归系数；h（t|z）表示故障率函数。基准风险函数h0（t）具有多种分布类型，当选用威布尔分布作为基准风险函数时，则称为威布尔比例故障率模型，其表达式如下：

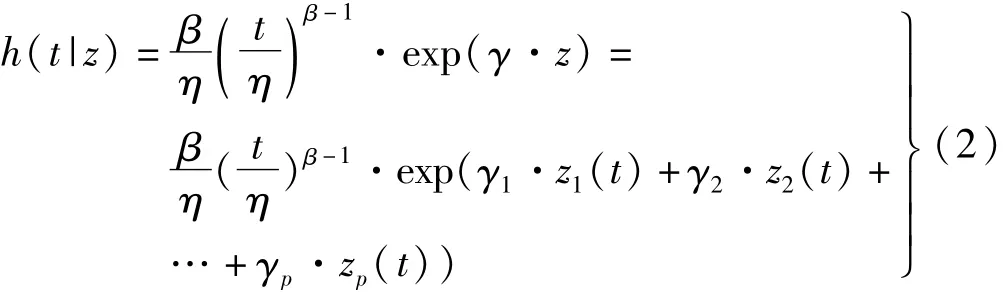
可进一步求出威布尔比例故障率模型的可靠度函数

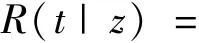
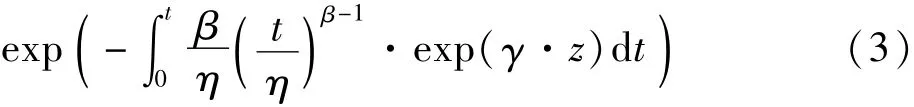
协变量的选取是进行比例故障率模型分析的关键。数控转台的振动信号是一种由内向外的状态量，振动状态的改变也标志着数控转台运行状态的相应改变，并且振动信号易采取，分析方法比较成熟，因此建立起振动信号与可靠性之间的关系是对传统可靠性分析方法的延伸和扩展。将提取的转台振动特征作为威布尔比例故障率模型的协变量，即可建立起基于振动特征的转台可靠性分析模型［16］。

从试验中采集到的振动信号，由于包含噪声，需要采用相应的振动信号处理方式进行分析，从而得到能反映转台运行状态的有效成分。对于振动信号的分析可以从时域、频域以及时频域（小波分析）3个方面进行。其中对于时域的分析主要包括对各个时域统计量的求解，对于频域的分析主要包括通过对信号的频谱分析、倒频谱分析和功率谱分析求解出一系列统计量（包括均方频率、频率方差、信噪比、边频带指数等），

而小波分析则是通过选取合适的小波基函数对原信号进行分解，以求得其低频、高频的细节成分，通过信号重构即可获得能反应原信号组成的各小波成分，进一步选取低、高频的多层次分解小波进行分析（包括谱峭度、谱能量等指标）。

虽然通过上述分析得到了表征转台运行状况的特征参数，但是特征向量的维数太大，且参数之间存在冗余，直接使用这些参数构建可靠性分析模型不仅会导致模型复杂，计算量变大，还会导致模型计算准确度下降。因此需要对上述提取的特征进行主成分分析，选取贡献率较高的主元作为后续建模的协变量。

主成分分析法（Principal Component Analysis，PCA）是数据分析中常使用的一种数据降维方法，通过将高维数据投影到低维空间的方式，在尽量不丢失原数据信息的基础上实现降低数据维度的效果。

利用PCA主成分分析后，最终选取了时域分析中的峰差、偏度、峭度、裕度因子，频域分析中的均方频率、重心频率、信噪比、信噪比及小波分析中的小波峭度、小波峭度这10个特征值作为表征数控转台运行状态的振动特征向量。

1.2 基于遗传算法的模型参数估计

建立了威布尔比例故障率模型之后，还需要根据实时获取的转台振动特征向量进行模型的参数估计。在求得形状参数β、尺寸参数η、协变量回归系数γ之后，才能进行可靠性评估。

常用的参数估计方法有最小二乘法、图估计法、矩估计法和最大似然估计法。最大似然估计法在处理多输入函数问题上具有明显的优势，因此最大似然估计法在可靠性领域具有广泛应用。但是，由于试验采取的转台振动特征向量维数太大，使用最大似然估计会导致计算复杂，且对于多个似然函数的优化很难取得全局最优解，因此本文提出了一种基于遗传算法优化的最大似然估计法用于参数的计算，具体流程如图1所示。

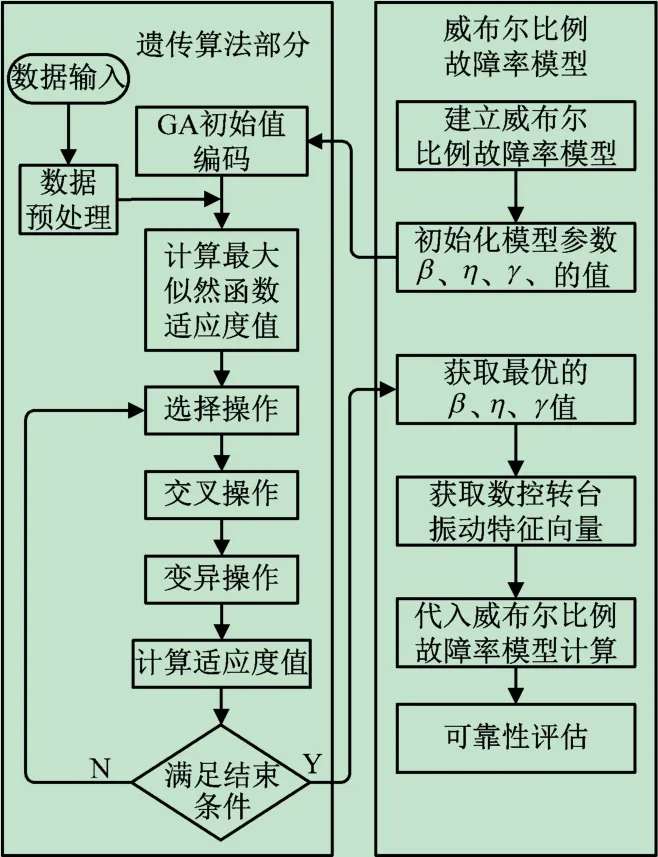
图1 基于遗传算法的优化威布尔比例故障率模型参数求解流程

对于威布尔比例故障率模型的参数估计，可构建如下所示的似然函数：

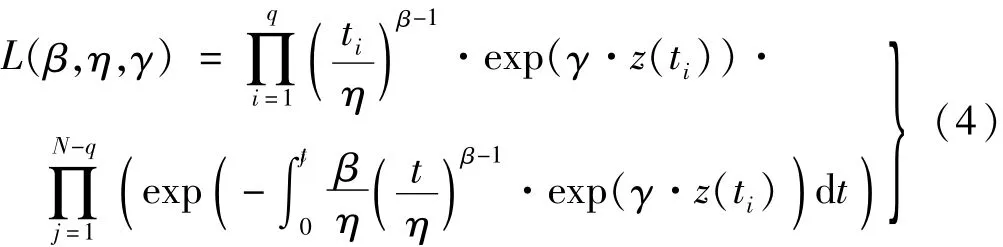
式中：q表示失效的样本数；N表示样本总数；z（ti）表示ti时刻的协变量观测值，在本文中为振动特征向量；z（tj）表示tj时刻的协变量观测值。

对上式两边同时取对数可得：

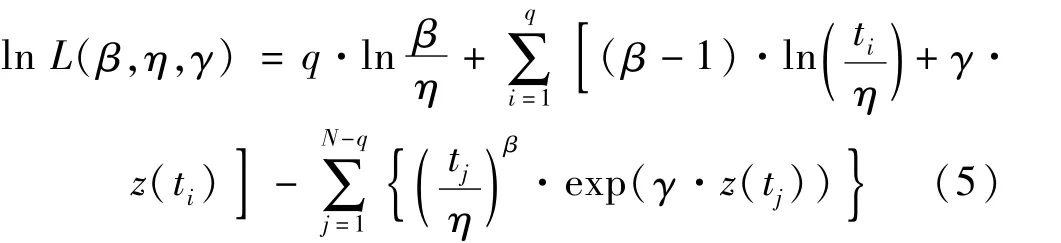
将威布尔比例故障率模型的似然函数作为适应度函数，表达式如下：

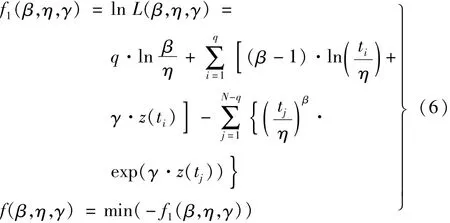
由于遗传算法求的是极小值，因此需要将适应度函数的最大值问题转换为其相反数的最小值问题进行求解。

2 数控转台振动特征提取试验方案

2.1 试验台结构分析

数控转台振动特性试验装置结构原理图如图2所示，实物如图3所示。

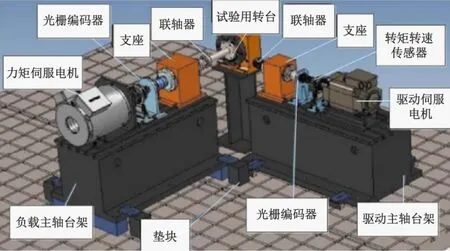
图2 数控转台性能实验装置结构原理图

图3 数控转台综合性能试验台

试验台主要由试验用数控转台、垫块、驱动电机、联轴器、加速度传感器、转矩转速传感器和信号采集系统组成。同时，本次试验用转台为国产TK13315E2型数控转台，相应的精度满足试验要求。

2.2 实验过程

2.2.1 转台运转试验

（1）检查试验设备是否正确安装，各个零部件是否正常。

（2）接通电源，启动冷却装置、驱动装置，使转台在各种转速下进行空载运转，具体的速度为：低速0.55 r/min、中低速3.3 r/min、中速5.5 r/min、中高速7.7 r/min，高速11 r/min。运行过程中检查装置的各个机构是否运行平稳，不能有阻滞，尤其是不能有明显的振动情况。在转台允许的转速范围里，分别进行低速、中速和中高速运转各40 h，以检验装置是否在各种条件下都能正常工作。

（3）设定数控转台中速空转，同时打开数据采集模块采集振动数据，观察采集卡和传感器能否正常工作，打开电脑上的数据收集软件观察是否有采集到数据。

2.2.2 转台振动特性试验

（1）检查传感器是否正确安装，启动实验装置，启动数据采集系统，依次检验连线是否正确，是否能够采集到传感器的数据。

（2）以正常数控转台和发生齿轮磨损故障的数控转台为试验对象，通过控制系统设定转台转速和负载的大小，本次试验采用的最大输出力矩为700 N·m。在运行过程中，让转台依次按照低速低载200 h、中低速中低载200 h、中速中载200 h、中高速中高载300 h、高速高载300 h的规律运行一段时间，采样频率为20 kHz，每隔4 h采集一次转台的振动数据，每次采集时间为5 s，采样长度为100×103。

如此设计实验的原因主要是考虑到在低速时振动并不明显，且一般转台也不会工作在低速低载的情况下，同时为了避免在做前面的试验时零件磨损太严重，导致在高速重载等情况下转台无法工作，因此设计为转速载荷越大试验时间越长，同时故障多发生于高速重载的情况下，这样也能收集到区分度较大的数据。

（3）完成上述试验后，需要对实验装置进行检查后再进行下一个试验，主要包括：①检查实验装置各部件以及传感器是否完好，对于已经损坏的部件，参照实验装置的技术说明进行替换；②在专业的技术工程师帮助下，检查连接部位是否损坏，更换新的联轴器等连接件。

3 实验结果与分析

3.1 数据预处理

通过上述试验，可以得到一系列传感器采集到的信号数据，经过采集系统处理后可将其转换为振幅、振速、加速度等数据。但是，由于测试环境存在各种干扰，使得传感器采集到的信号与真实数据有一定的差距。如果不进行数据的预处理，减少采样数据的干扰成分，可能会导致后续的分析得出错误的结论。常用的数据预处理方法如下：

（1）消除趋势项。由于压电式传感器存在零点漂移现象，往往收集到的信号会偏离基线，而这个过程就称为信号的趋势项。

（2）数据降噪处理。不能对收集到的信号进行直接处理，需要使用合适的降噪方法提取有用的信息，这也是进行后续数控转台可靠性评估的基础。小波包分析在处理非平稳信号、去除信号噪声方面表现出很大的优越性，能有效提高信噪比。

（3）数据平滑处理。在对收集到的数据进行消除趋势项和降噪处理后，由于信号的干扰，绘成的振动曲线转折处会形成很多毛刺，后续分析前需对数据进行平滑处理。

3.2 结果分析

由于传感器收集到的振动值往往在一个时间段内是变化很小的，不利于后续的信号处理操作，因此将去除无效值后的每组数据等间隔选取600个数据点合成新的振动信号代替原信号进行后续分析。

由于特征向量的维数太大，在代入威布尔比例故障率模型进行计算之前还需进行数据标准化以提高后续威布尔比例故障率模型参数估计的速度和精度。本文采用的是离差标准化，通过线性变换将原始数据映射到［0，1］之间，转换函数如下：

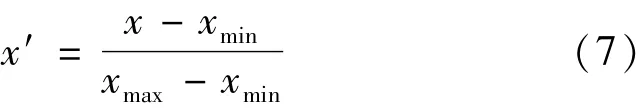
利用前面制定的特征提取方法，得到部分特征值如图4～图7所示。由图4～7可见，峰差、峭度、偏度和裕度因子这4个特征在150点以后出现了剧烈的变化，说明转台在载荷和转速较高的情况下振动特征会有较明显的变化。同时使用齿轮磨损故障的数控转台试验时，多个特征指标与正常情况都有明显的区别，因此证明了提取的转台特征向量能够很好地表征转台的运行状况。

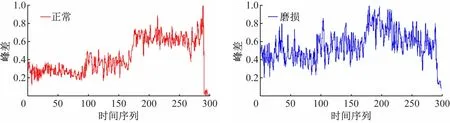
图4 正常状态和磨损状态下的峰差变化

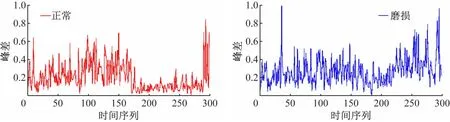
图5 正常状态和磨损状态下的峭度变化

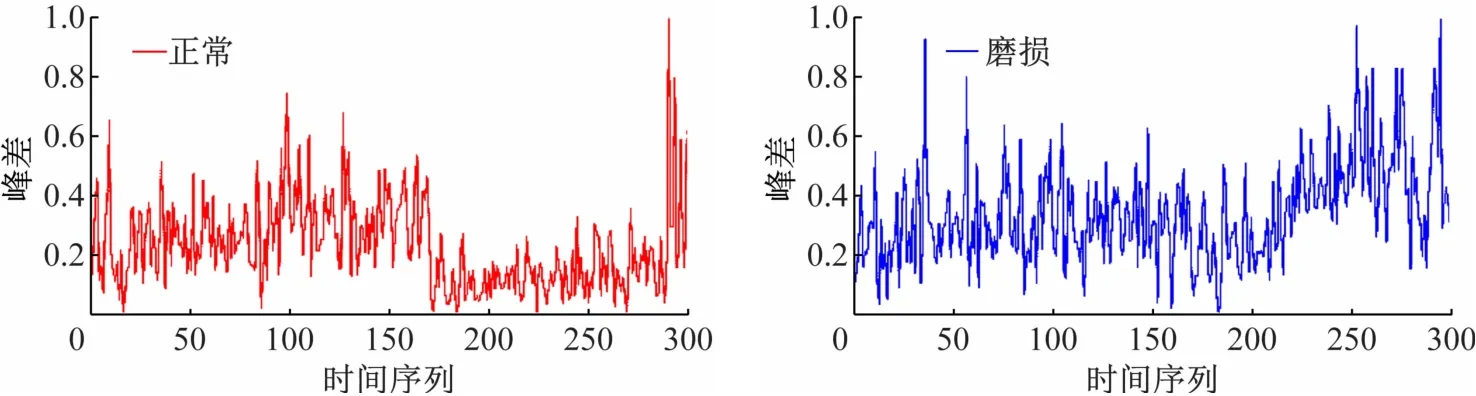
图7 正常状态和磨损状态下的裕度因子变化

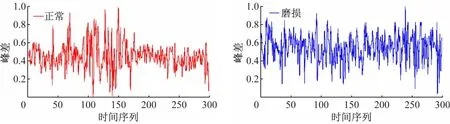
图6 正常状态和磨损状态下的偏度变化

将计算后的振动特征向量代入威布尔比例故障率模型，利用基于遗传算法优化的最大似然估计法进行参数估计，经过迭代运算后可得威布尔比例故障率模型的各参数估计。从而，可求得转台在正常工作状态和齿轮磨损工作状态下的可靠度，如图8所示。从图8可以看出，随着工作时间的增加，数控转台可靠度逐渐降低。在正常状态下的可靠度约为0.98，而齿轮磨损状态下的可靠度约为0.5，与实际工作情况基本一致。在工作时间为600 h左右时，两种工作状态下的转台可靠度均出现较大的变化，可以看出振动特征的变化会导致可靠度的明显变化。综上分析，基于振动特征的威布尔比例故障率模型可以准确的根据转台运行状态进行可靠性评估，说明了基于振动特征的威布尔比例故障率模型在可靠性分析中的有效性。

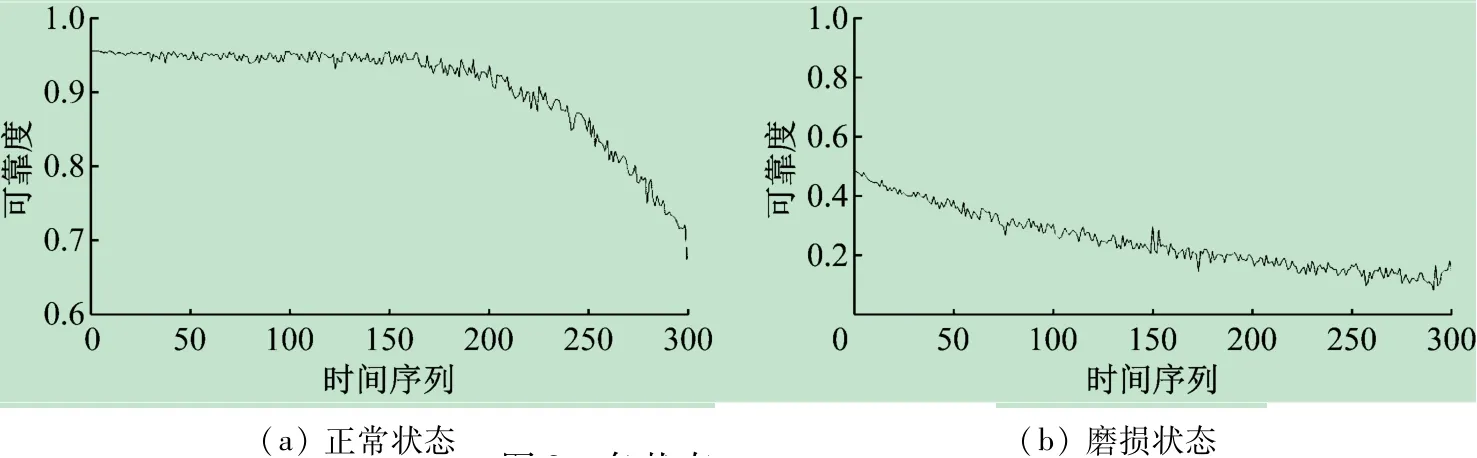
图8 各状态下的可靠度变化

4 结 语

基于历史故障数据的可靠性分析方法一般需要大量的历史故障数据做基础，但是失效数据的积累是非常缓慢的，往往需要做大量的可靠性试验，并且这种分析方法并没有考虑到设备的运行状态。因此对于数控转台这种实时工作状态对加工结果具有决定作用的设备采取这种分析方法是不准确的。本文以国产TK13系列数控转台为研究对象，为了弥补传统可靠性分析方法的不足，提出了一种基于振动特征的数控转台实时可靠性评估方法。通过将转台振动特征作为协变量，构建了威布尔比例故障率可靠性模型，并通过试验分析了模型的有效性。