摆动行波及其向定常对流的过渡
2022-04-06宁利中宁碧波田伟利
宁利中,袁 喆,宁碧波,田伟利
(1.西安理工大学 水利水电学院,西安 710048;2.嘉兴学院 建筑工程学院, 浙江 嘉兴 314001;3.上海大学 建筑系, 上海 200444)
0 引 言
对Rayleigh-Benard对流问题的研究,已经有百年的历史,也获得了丰富的研究成果[1-3]。特别是最近几十年来,对于分离比(Separation ratio)ψ<0的混合流体对流的研究,获得了许多有趣的行波对流斑图。在理论探讨方面,利用流体力学振幅方程组[4-5]的数值模拟解释了行波现象;利用流体力学扰动方程组[6-8]和流体力学基本方程组[9-17]的数值模拟再现了复杂的对流行波结构,进一步发现了摆动行波,具有缺陷的行波,缺陷源周期摆动的对传波斑图等[9-18],并揭示了混合流体对流的运动机理。
摆动行波是其中一种有趣的对流斑图[19]。利用振幅方程,Busse小组研究了摆动行波的稳定性[20-21]。Knobloch E等[22]通过简单模型模拟了摆动行波。笔者通过流体力学方程组的数值模拟发现ψ比较小时的摆动行波状态[19,23],Zhao B X等[24]的数值模拟也证实了这一特性。桥野恭央[25]在实验中发现了ψ比较大的摆动行波斑图,这说明摆动行波状态是一种新的斑图。另外,关于混合流体对流运动的数值模拟[26-28]和利用格子Boltzmann方法对Rayleigh-Benard对流的数值模拟[29-30]也获得许多进展。可是,基于流体力学方程组的数值模拟对摆动行波状态的详细研究报道较少。本文将主要通过流体力学方程组的数值模拟探讨具有强Soret效应的混合流体摆动行波对流的时空结构特性及其向定常对流过渡的动力学特性。
1 数学物理模型
考虑填满混合流体的矩形腔体,下部加热,上部温度保持恒定,当上下温度差超过临界值时,腔体中对流发生。对流见图1。

图1 矩形腔体中的对流

式中:u(u,0,w),T,C,p,t,ν,D,ez,ΔT,ST,α,β分别表示速度矢量、温度、浓度、压强、时间、运动黏性系数、浓度扩散系数、z方向的单位矢量、上下壁面的温度差、Soret系数、热产生的体积膨胀系数、浓度引起的体积膨胀系数。下标0表示对应物理量的参考值。
由于所有壁面都是固定的,速度在壁面上为0。浓度流在壁面上是不可穿透的。故速度和浓度流的边界条件为
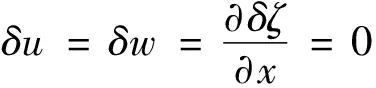
(5)

(6)
式中:δu,δw分别为水平流速,垂向流速;Γ为长高比。
由于温度在上下左右壁面处是绝热的,在上下壁面z=0,1处是等温的,故温度的边界条件为

(7)
当z=0时,
δT=0.5
(8)
当z=1时,
δT=-0.5
(9)
在数值计算中,根据有限容积法对混合流体对流的流体力学方程组进行了离散,流体力学方程的对流与扩散项采用二阶精度的乘方差分格式。离散中采用均匀交错网格系统,模拟几何区域划分为242×22或362×32个网格节点,Simple算法用于求解速度-压力耦合方程,离散方程采用TDMA法求解。时间步长为Δt=0.001。当ψ=-0.4,Pr=13.8,Le=0.01,r=1.95时,在上面两种不同密度的网格下模拟得到了一致的结果,因此,验证了数值模拟结果对于不同疏密网格的独立性。为了节约计算资源,计算中采用了242×22的网格密度。
计算的初始流动条件为,流动的微小振幅的包络线具有高斯分布。混合流体的物性参数为ψ=-0.6,Pr=13.8,Le=0.01, 长高比Γ=12。
2 摆动行波及其向定常对流的过渡
2.1 摆动行波
2.1.1 摆动行波斑图的形成
对于分离比ψ=-0.6的混合流体,计算发现在r∈(6.7,11.2]内存在摆动行波斑图。首先分析r=6.8、10.0、11.2时摆动行波斑图的形成。r=6.8时摆动行波斑图的形成过程见图2(a),在对流发生的初始阶段,腔体内首先出现以竖直中心方向为对称轴,两侧流体左右摆动的对传波状态。随着时间的推移,在t=12时,上述状态破坏,所有的滚动开始向左传播;t=20左右,行波转向,开始向右传播,最终形成保持稳定周期的摆动行波。r=10.0时摆动行波斑图的过渡过程见图2(b),对流发生的初始阶段,发生暂短的对传波后,在t=14以后腔体内行波过渡到摆动行波斑图。r=11.2时摆动行波斑图的过渡过程见图2(c),经过初始阶段的极其短暂的对传波后,在t=10时形成稳定的摆动行波斑图。由图2可见,随着r增大,向摆动行波斑图过渡的时间变短,也即稳定的摆动行波斑图形成的越快;随着r增大,摆动行波斑图的摆动周期变小,摆动幅度也变小。随着时间的发展,摆动行波斑图的摆动逐渐规则、光滑,它的摆动周期也趋于稳定。
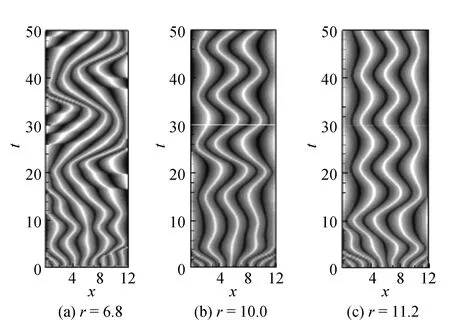
图2 摆动行波斑图的过渡过程
2.1.2 摆动行波斑图的结构
相同时间间隔内,图2参数情况下稳定摆动行波斑图的腔体高度1/2处温度分布随时间的变化见图3。由图3可见,随着r的增大,摆动行波斑图的摆动变得更加光滑,摆动幅度减小,摆动周期变短。摆动行波斑图的摆动周期Tu随着r的变化关系曲线见图4。由图4可见,摆动行波斑图的摆动周期随着r的增加而减小,当r>8以后,随r的增加,摆动周期减小的速度变慢。
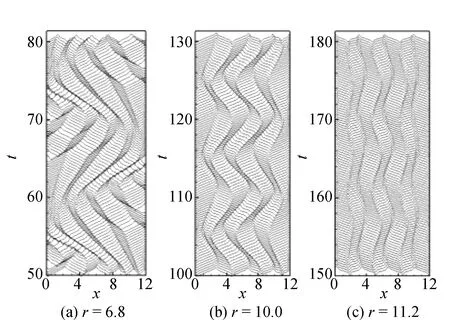
图3 腔体1/2高度处的温度场随时间的变化

图4 摆动周期Tu随相对瑞利数r的变化
r=10,t=102.8~112.7时间间隔内,腔体内摆动行波斑图的流线随着时间的变化见图5。其中,横轴为腔体的长度方向,纵轴的每个长矩形框中的图像为腔体内流线分布,每两个长矩形框之间的时间间隔为Δt=0.9。可见,腔体内出现7个流线圈,也即系统发展成3个半周期的对流滚动。在t=102.8时摆动行波斑图向腔体左侧传播,这时,左侧的流线圈被挤压变小,右侧的流线圈扩张变大,左侧的流线圈的波长减小,波数增加,相应的右侧的流线圈的波长增加,波数减小;当t=104.6时右侧流体的流线圈得到充分的扩展,左侧流体的流线圈被挤压,由于其内部机理,向左运动的流体滚动开始反转方向,开始向右侧运动;当t=111.7时左侧流体的流线圈得到充分扩展,右侧流体的流线圈被挤压变得最小,这时,左侧的流线圈的波长增加,波数减小,相应的右侧的流线圈的波长减小,波数增加;随着时间的发展,腔体内的摆动行波斑图循环传播下去。

图5 r=10.0时流线的时空结构
2.2 摆动行波斑图向定常对流状态的过渡
随着相对瑞利数r的增大,对于r=11.3的情况,腔体内t=3时先由短暂的对传波过渡到摆动行波斑图,这种状态一直保持到t=133时,系统过渡到定常对流状态,对流滚动不再向左或向右来回传播,而是保持原位置连续的滚动,黑白色的上升流和下降流位置随时间不再空间变化,在竖向时间轴线上呈现为一条竖向直线见图6。r=11.3时腔体内最大垂直流速δwmax随时间的变化见图7,它也反眏了摆动行波斑图向定常对流的过渡性质。可见t≤133时,最大垂直流速δwmax随着时间一直在规则的平稳的周期变化,系统是摆动行波斑图状态。当t>133时,最大垂直流速稳定在δwmax=52,最大垂直流速不再随着时间变化,最大垂直流速δwmax随时间的变化变成一条水平线,这时,摆动行波斑图转变成定常对流状态。

图6 r=11.3时腔体1/2高度处温度场的时空结构
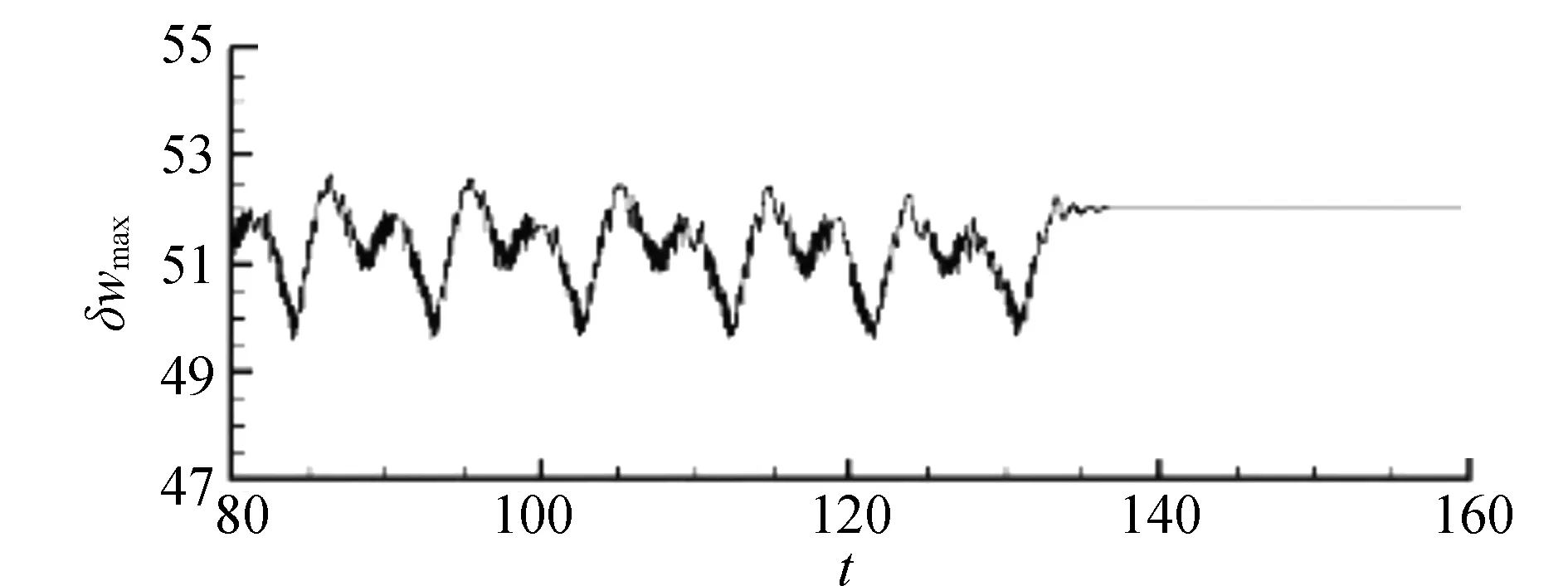
图 7 r=11.3时最大垂直流速δwmax随时间的变化
r=11.3时定常对流状态时腔体内的对流场见图8。图8(a)为速度矢量分布,腔体内出现7个对流滚动圈,它们的大小基本相同,可见上升流和下降流的位置,在上升流和下降流的位置处垂直流速具有最大值。图8(b)为流线图,流线图为7个光滑的曲线圈。图8(c)为浓度分布,在上升流和下降流的位置处存在明显的上升羽状分布和下降羽状分布。
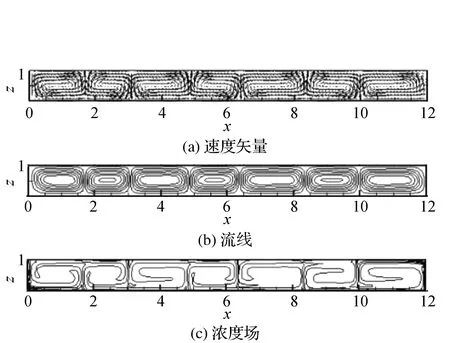
图8 r=11.3时定常对流的对流场(t=408)
为了探讨向定常对流的过渡过程,又对r>11.3的不同r进行了计算。发现在这些不同的r下腔体中的对流最终都发展成定常对流状态。r=12.0、16.0、20.0时定常对流状态的形成过程见图9。由图9可见,系统先过渡到摆动行波斑图,后发展成定常对流状态,过渡过程不同。随着r的增大,发展成定常对流状态的所需时间逐渐减小。不同r下过渡到定常对流的时间见表1。由表1可见,随着r的增加,由摆动行波斑图过渡到定常对流的时间迅速变短,定常对流状态越容易出现。

表1 不同r时过渡为定常对流状态时对应的时间
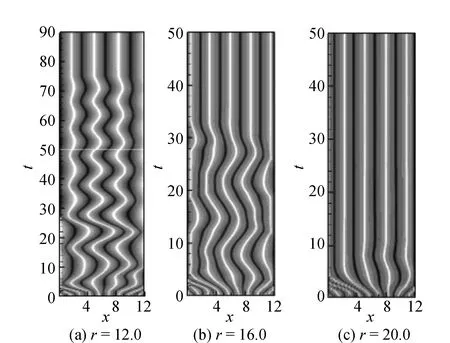
图9 向定常对流的过渡
3 结 论
本文利用Simple算法对混合流体对流的流体力学基本方程组进行了数值模拟,探讨了矩形腔体具有强Soret效应的混合流体对流的摆动行波斑图的动力学特性及其向定常对流过渡的动力学特性。
1)发现在较大的相对瑞利数变化范围内存在着摆动行波。在摆动行波存在的范围内,系统从小扰动状态发展成摆动行波的时间随着相对瑞利数的增加而减小。
2)摆动行波的摆动周期和摆动幅度随着相对瑞利数的增加而减小。摆动行波的当地波长随着时间被压缩或者伸长,当地波数随着时间和空间不断变化。
3)当超过了摆动行波存在的上限后,系统首先由具有小振幅的扰动状态发展成摆动行波,然后经过一段时间的过渡瞬态的摆动行波发展成定常对流。从摆动行波过渡到定常对流的时间随着相对瑞利数的增加变短。本文是加热混合流体对流的基础研究,对实际工程中存在的加热混合流体对流的问题有一定的应用前景。
