界面约束对石墨烯/环氧树脂纳米复合材料弹性性能影响有限元分析
2022-04-05杨绍钊黄立新
杨绍钊, 黄 君, 黄立新
(广西大学 a.土木建筑工程学院; b.工程防灾与结构安全教育部重点实验室, 南宁 530004)
0 引 言
石墨烯具有良好的导电[1]、 吸附[2]、 力学等性能[3], 呈现出巨大的应用潜力。石墨烯具有极高的强度和杨氏模量, 是纳米复合材料非常理想的纳米增强材料。在石墨烯改善复合材料力学性能方面, 通过不同的实验方法已取得许多成果:高锋等[4]研究石墨烯微片含量对氰酸酯树脂的影响, 发现当石墨烯含量为10%时, 复合材料的拉伸模量为3.72 GPa, 与纯基体相比提高18.47%; Zandiatashbar等[5]采用纳米压痕法研究了不同质量分数的环氧石墨烯纳米复合材料的蠕变行为, 在较高的应力和温度条件下, 0.1%的纳米复合材料的蠕变变形明显小于未填充聚合物时的情况。在数值模拟方面, Guo等[6]通过三维多尺度仿真的有限元方法, 采用石墨烯的空间框架结构分析其体积分数和不同倾角对聚合物基复合材料力学性能的影响, 结果表明, 随着石墨烯体积分数增大和倾角减小, 复合材料杨氏模量和剪切模量显著增加; García-Macías等[7]利用Mori-Tanaka模型模拟并计算了石墨烯增强复合材料的宏观弹性模量, 结果表明, 石墨烯增强复合材料板在随机定向的填充结构中具有良好的承载能力。
石墨烯与基体界面粘结力的强弱对纳米复合材料性能的增强是关键性的, 因此界面粘结力的研究引起研究人员的关注: Li等[8]通过拉曼光谱研究发现基体与增强材料间存在极强的界面相互作用, 当石墨烯的有效含量达到1.5%时, 聚丙烯的拉伸强度和储能模量分别提高了18%和33%; 黄海新等[9]采用石墨烯和多壁碳纳米管混合改性环氧胶粘剂, 当混合物含量为0.5%时, 环氧胶粘剂的剪切强度提高了34.52%; Giannopoulos等[10]采用线性弹簧单元及混合有限元法对石墨烯纳米复合材料进行力学行为模拟, 随着石墨烯体积分数的增加, 界面的粘结强度增大, 应力传递效果越显著。
本文建立了石墨烯/环氧树脂纳米复合材料的代表体单元(representative volume element, RVE), 并通过有限元计算预测复合材料的弹性性能。在ABAQUS建模中, 分别采用Euler-Bernoulli梁单元和六面体线性单元离散石墨烯片和环氧树脂基体, 以嵌入区域约束、 强绑定约束和弱绑定约束模拟石墨烯和环氧树脂基体之间界面的粘结作用并通过数值算例讨论界面约束对石墨烯纳米复合材料弹性性能的影响。
1 嵌入式代表体积单元
1.1 嵌入式代表体积单元模型
石墨烯纳米复合材料微观结构是不均匀的, 从而微观上性质也是不均匀的。通过引入代表体积单元的方法, 将不均匀纳米复合材料结构的力学分析问题转化为均质化后相同结构的力学分析问题。对均质化结构的力学分析得到纳米复合材料的等效弹性性能。如图1所示, 对于定向非连续纳米复合材料结构, 选取嵌入式代表体积单元模型(简称嵌入式模型), 石墨烯包含在基体中间。该单元的尺度相对于石墨烯纳米复合材料结构尺度充分小, 同时又包含有代表性的石墨烯, 故嵌入式代表体积单元[11]的平均性质能够描述石墨烯定向非连续纳米复合材料宏观有效性质。

图1 嵌入式代表体积单元模型
1.2 嵌入式代表体积单元模型尺寸的确定
假设整个嵌入式模型的尺寸为Lc×Wc×Tc(长×宽×高), 如图2所示, 片状石墨烯在环氧树脂基体的几何中面上均匀分布, 且石墨烯3个方向的外边界到整个模型的外边界的距离均为t。取石墨烯片的尺寸为10.091 nm×10.089 nm×0.34 nm(Lg×Wg×Tg), 体积含量Vfr分别为1.12%、 2.5%、 5%、 7.5%和10%, 得到5种不同尺寸的模型。由模型的几何关系可知:
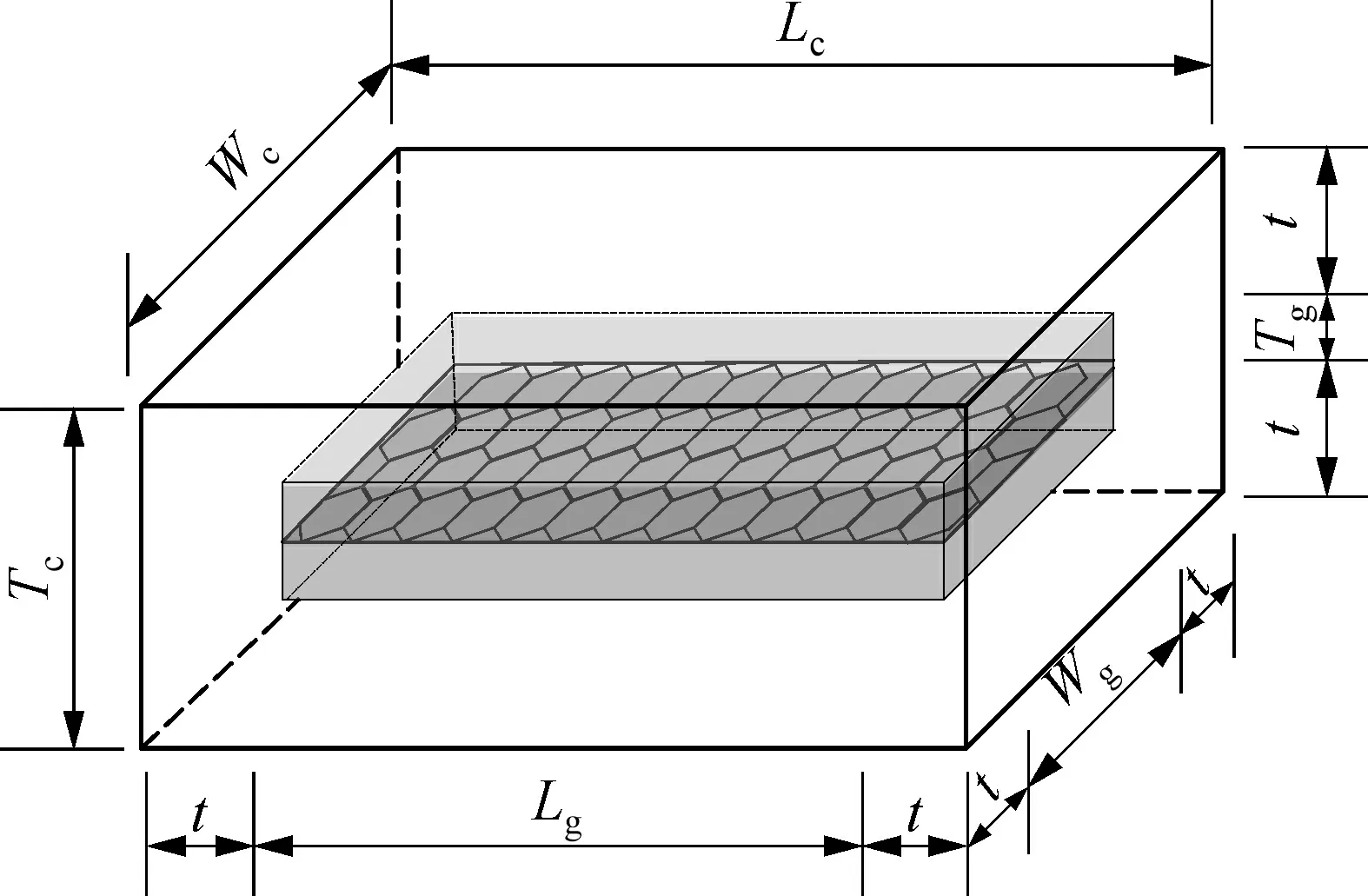
图2 嵌入式代表体积单元模型尺寸示意图
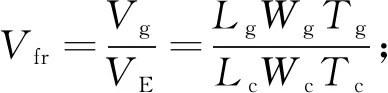
(1)
Lc=Lg+2t,Wc=Wg+2t,Tc=Tg+2t;
(2)
LcWcTc=(Lg+2t)(Wg+2t)(Tg+2t)。
(3)
其中,Vg和VE分别为石墨烯和嵌入式模型的体积。联立式(1)~(3)可求得Lc、Wc、Tc和t的值, 表1列出的计算结果是5种模型的尺寸参数。
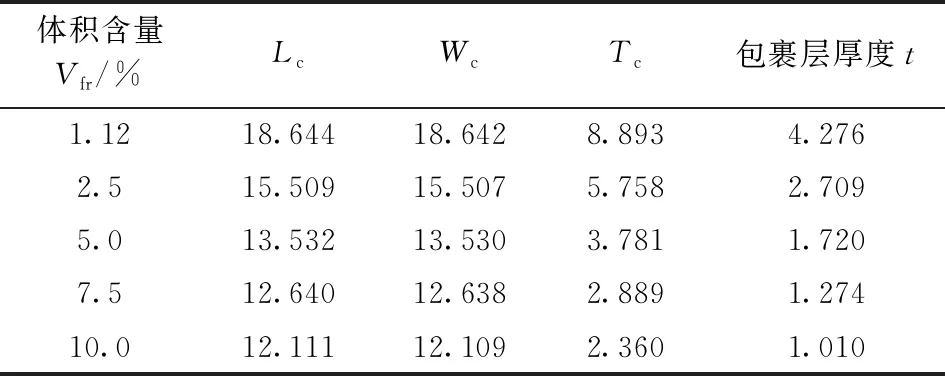
表1 不同石墨烯体积含量下嵌入式模型的尺寸参数
1.3 杨氏模量Ecx的计算
由单轴拉伸试验[12]测定复合材料力学性能的方法通过对嵌入式模型进行拉伸行为模拟, 计算石墨烯复合材料x方向的杨氏模量Ecx。如图3所示, 嵌入式代表体积单元是对称的, 取1/4结构进行受力分析。由于对称, 1/4结构在x=0边界面上x方向的位移为零; 在y=0边界面上y方向的位移为零。
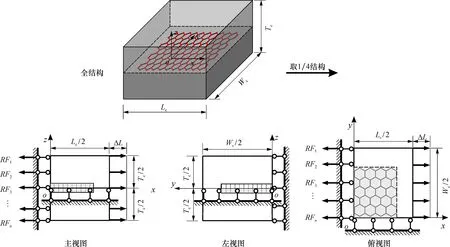
图3 嵌入式模型单轴拉伸受力图
对x=Lc/2边界面施加微小位移ΔL=0.001 nm。通过ABAQUS计算后提取x=0面内所有结点的支座反力RFi, 再通过下式计算出Ecx:
(4)
(5)
(6)
其中:σave是位移面内的平均应力;εx是拉伸方向上的正应变。拉伸过程属于线弹性和小变形的受力过程, 故采用未发生位移前的截面尺寸进行计算。
2 嵌入式代表体积单元的有限元建模
2.1 单轴拉伸理论模型
有限元分析前, 根据单轴拉伸问题给出具有特征结构的1/4结构模型如图3所示。片状石墨烯在环氧树脂基体的几何中面上, 图中标示出了石墨烯的几何中面位置, 不对其厚度作特别标注, 实际计算时仍然考虑石墨烯的厚度。单轴拉伸力学行为采用位移特征进行描述, 位移特征在有限元分析中以约束方式保证, 有限元分析过程中主要分为初始分析步和一般分析步, 表2列出了本文模型有限元分析过程中各分析步的约束条件。

表2 有限元各分析步的约束条件
2.2 石墨烯片和环氧树脂基体的有限元建模
石墨烯结构是碳原子之间相互围成蜂窝形的二维网状结构, 在研究石墨烯二维网状结构的弹性性能中, Sakhaee-Pour[13]采用圆截面梁单元模拟共价键(C—C)中碳原子间的作用力。基于Sakhaee-Pour的概念, 本文在ABAQUS软件中采用Euler-Bernoulli梁单元(B33)进行石墨烯片的建模。为了描述B33梁单元的有关参数, 下文仅列出梁单元有关参数计算的关键公式和概念, 详细内容参见文献[13]。
如图4所示, 采用圆形截面梁单元模拟碳碳共价键中原子之间的作用力, 梁单元的变形可以真实反映共价键的拉伸、 弯曲和扭转3种类型的形变。
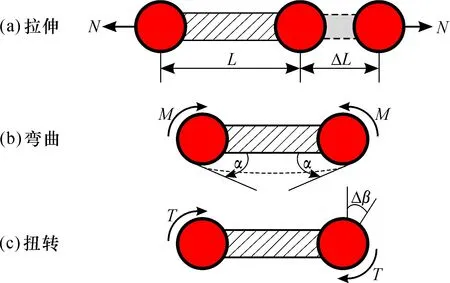
图4 B33单元受力分析
根据分子力学原理, 将共价键的拉伸势能、 键角弯曲势能、 二面角扭转势能等价于等效梁单元相应的应变能, 可以得出分子力学常数kr、kθ、kτ与等效梁单元抗拉刚度EA、 抗弯刚度EI以及抗扭刚度GJ之间的关系, 即
kr=EA/L=Eπr2/L;
(7)
kθ=EI/L=Eπr4/(4L);
(8)
kτ=GJ/L=Gπr4/(2L),
(9)
其中:L是梁单元的长度, 等于两个碳原子之间的距离, 取值为L=0.142 1 nm[13]。
由文献[13]提供的分子力学常数, 根据式(7)~(9)计算得到梁单元的杨氏模量E和圆截面半径r等材料参数和几何参数, 如表3所示。

表3 等效结构梁单元模型的参数
嵌入式代表体积单元的环氧树脂基体可以视为各向同性材料, 在有限元软件ABAQUS中采用8结点六面体线性单元(C3D8)进行建模, 杨氏模量、 泊松比分别取Em=3.8 GPa和νm=0.4[14]。石墨烯和环氧树脂基体的单元类型和嵌入式代表体积单元模型的网格划分如图5所示。

图5 嵌入式代表体积单元的有限元网格
2.3 采用不同约束模拟界面的粘结作用
为了更好地模拟石墨烯和环氧树脂基体之间界面的粘结作用, 本文在ABAQUS中分别采用了嵌入区域(embedded region)约束和绑定(tie)约束定义石墨烯和环氧树脂基体间的接触行为。嵌入区域约束允许在模型的主机区域放入内置石墨烯片, 不需要考虑嵌入位置是否为空, 并且省去了合并两个基体部件的时间; 而绑定约束可将石墨烯片和两个基体的接触面连接在一起, 相当于两个面的刚性连接, 这一对接触面在整个分析过程中始终紧密接触, 绑定区域不发生相对运动和变形, 绑定约束关系建立之前需要完成石墨烯与两部分基体之间的部件装配。
如图6所示, 两者的不同之处在于, 嵌入区域约束可在石墨烯与基体之间存在干涉的情况下建立, 将石墨烯嵌入到环氧树脂基体中不需要考虑其嵌入的位置结构是否为空, 约束区域单一且不可调整; 绑定约束的两个部件之间不存在干涉, 但约束位置和区域可灵活调整。
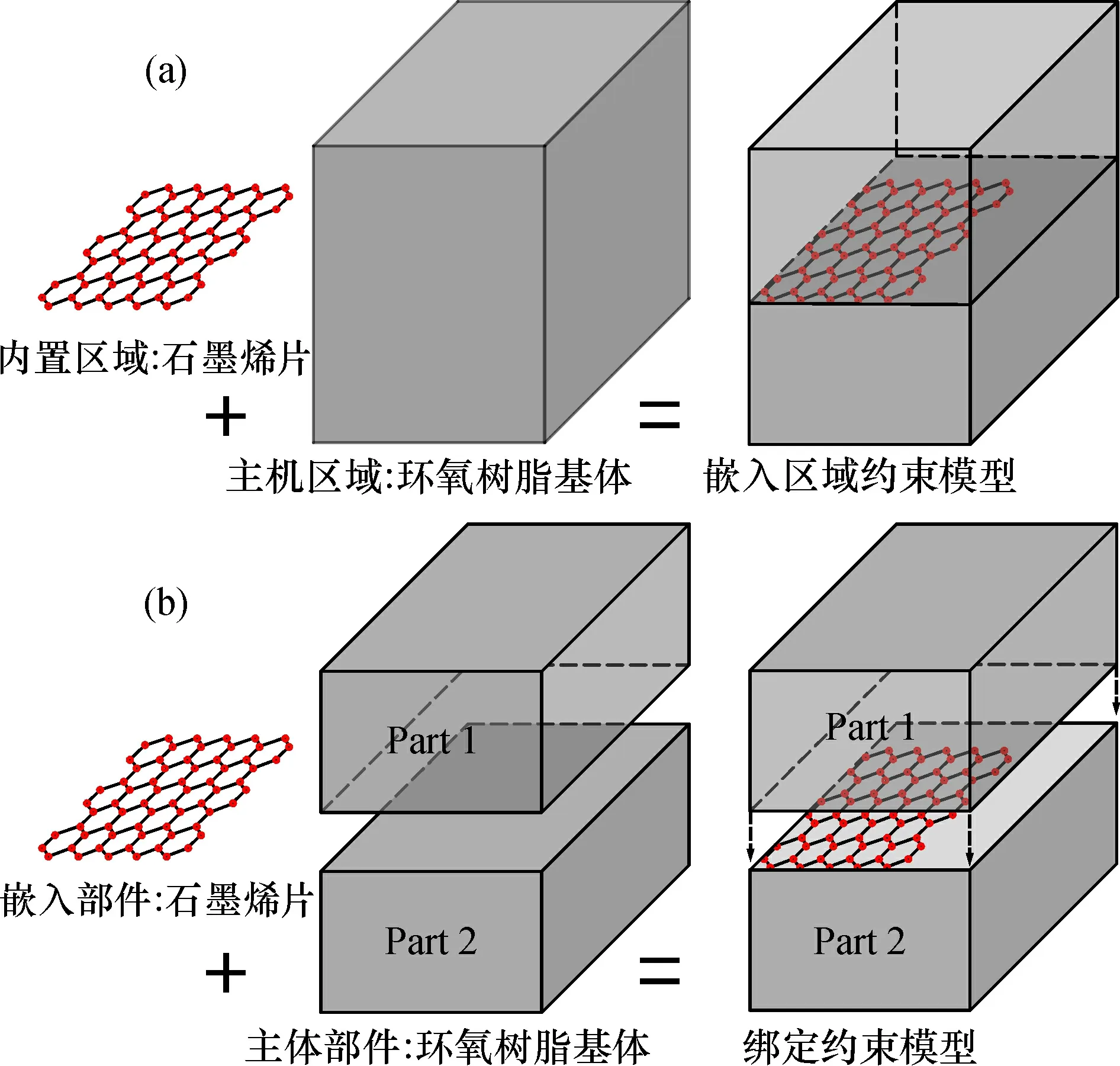
图6 嵌入区域约束(a)与绑定约束(b)模型对比
本文基于绑定约束的可调性, 将其分为强绑定约束和弱绑定约束。强绑定约束是指同时在两相的上下表面和侧面进行结点绑定, 而弱绑定约束是指仅在石墨烯和基体接触的上下表面进行结点绑定, 两者的区别如图7所示。表4给出以上3种约束的界定方式。

图7 强绑定(a)与弱绑定(b)约束模型对比
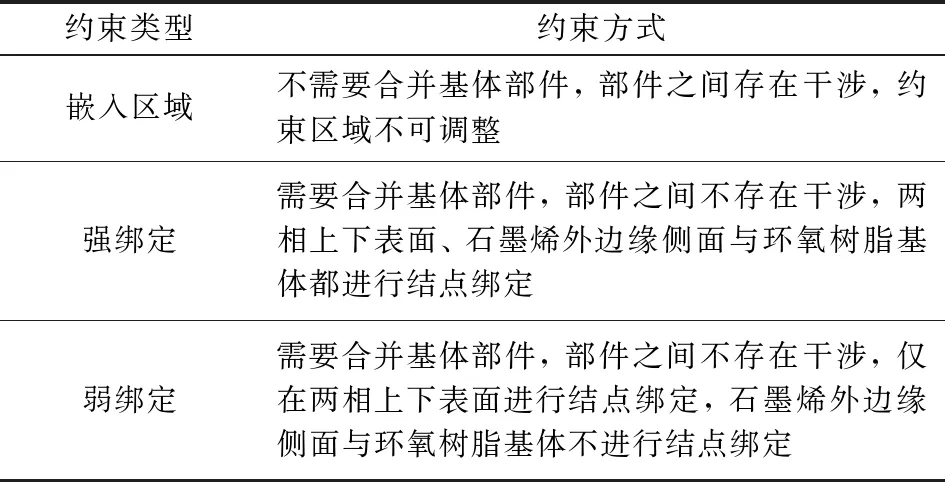
表4 3种约束的界定方式
3 算 例
3.1 完好界面不同约束对等效弹性性能的影响
石墨烯纳米复合材料中的石墨烯与环氧树脂基体界面分别采用嵌入区域约束、 强绑定约束和弱绑定约束进行模拟。Halpin-Tsai理论模型[15]适用于定向非连续纳米复合材料结构的弹性模量预测, 因此通过与Halpin-Tsai理论模型结果对比, 分析这3种界面约束对石墨烯/环氧树脂纳米复合材料弹性性能的影响。
Halpin-Tsai方程通过内插法近似表达了复杂细观力学行为的结果[16], 其计算公式为
(10)

(11)
ξ=2Lg/(3Tg),
(12)
其中:Ecx、Em和Eg分别为复合材料、 基体和石墨烯的弹性模量,Eg=1 000 GPa,Em取值与前节相同;ξ是石墨烯增强作用的量度, 根据其几何形状和排列方式按式(12)进行计算;ηL表示纤维长度有效因子。
表5给出了在3种界面约束的情况下纳米复合材料杨氏模量的计算结果。可见, 本文解与Halpin-Tsai解的最大偏差为3.58%, 吻合较好, 说明这3种界面约束建立的模型都是准确可靠的。将体积含量为1.12%的石墨烯/环氧树脂模型的归一化杨氏模量Ecx/Em与Rafiee[17]的试验值进行对比, 如表6所示。

表5 不同体积含量和约束方式对应的复合材料杨氏模量
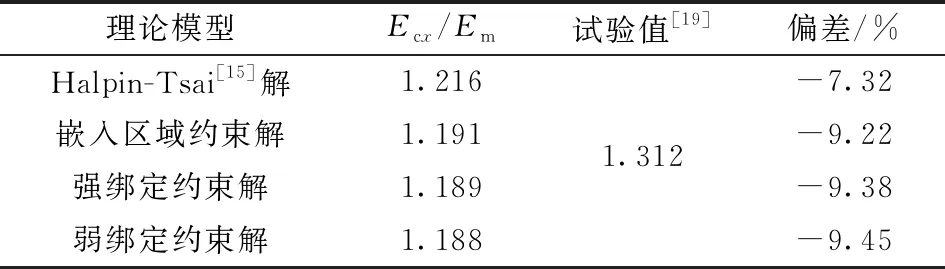
表6 Vfr=1.12%的石墨烯/环氧树脂复合材料杨氏模量的模拟值与试验值
4种模型中, Halpin-Tsai解与试验值的偏差最小, 为7.32%; 弱绑定约束解与试验值的偏差最大, 为9.45%。由此可见, 理论计算值比实测值偏小, 与理论模型相比, 试验中石墨烯与环氧树脂界面层之间产生的粘结作用更强。
各种石墨烯体积含量下的嵌入式代表体积单元模型在沿x方向拉伸下的变形和受力分布具有相似性。图8为石墨烯体积含量为5%时, 模型在嵌入区域约束、 强绑定约束和弱绑定约束作用下沿x方向单向拉伸时,x=0界面的应力和反力图。

图8 3种约束模型模拟云图
从反力图可以看出, 嵌入区域约束模型的结点支座反力最大值出现在石墨烯片的约束结点上, 并且石墨烯片的约束结点都呈现比较大的反力值; 强绑定约束模型结点支座反力最大值也出现在石墨烯片的约束结点上, 但是只有少量墨烯片的约束结点有较大的反力值; 弱绑定约束模型的结点支座反力最大值出现在环氧树脂基体约束结点上。在x=Lc/2边界面施加微小位移ΔL=0.001 nm, 通过力的传导, 在x=0界面结点支座处3种约束模型的反力出现不同的分布现象, 这说明了嵌入区域约束模型能够更好地模拟石墨烯与环氧树脂基体界面间的粘结作用, 反映界面之间的应力传递关系。从应力图发现, 在x=0界面, 嵌入区域约束模型的应力均为拉应力, 而强绑定约束模型和弱绑定约束模型的应力均出现压应力, 这也说明嵌入区域约束模型有良好的应力传递关系。
如图9所示, 在3种界面约束的情况下, 纳米复合材料的杨氏模量随石墨烯体积含量变化而变化。 随着石墨烯的体积含量增大, 杨氏模量呈线性增长趋势。当Vfr达到10.0%时, 纳米复合材料的杨氏模量提高到环氧树脂的3倍以上。
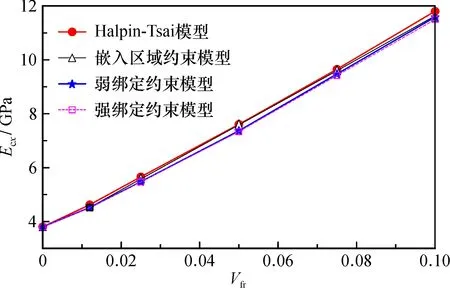
图9 石墨烯含量对杨氏模量的影响
3.2 界面脱粘对等效弹性性能的影响规律
石墨烯/环氧树脂复合材料的制备中可能会出现脱粘的现象, 主要包括中心区域脱粘和边缘区域脱粘。本节讨论粘结界面回字型分区脱粘对石墨烯/环氧树脂纳米复合材料弹性性能的影响, 取强绑定约束模型进行模拟界面的粘结情况。如图10所示, 将石墨烯和环氧树脂基体的粘结界面分成4个回字型区域, 并使每个区域的面积相等, 环形区域往x和y方向上等比例扩展, 石墨烯内部几何中心往外区域依次编号为1、 2、 3、 4, 即满足:
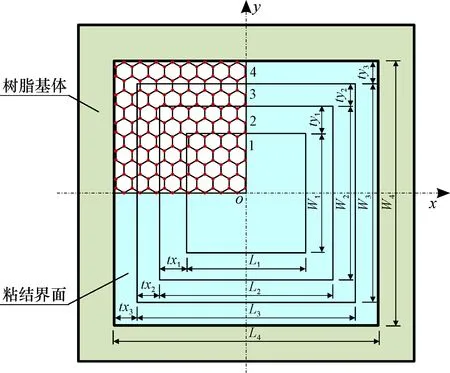
图10 脱粘区域划分
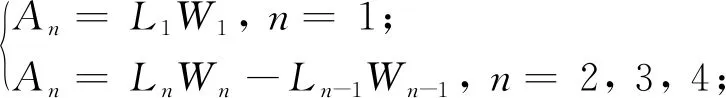
(13)
(14)
(15)
其中,Ln、Wn和An分别为每个区域的长度、 宽度和面积(n=1时为矩形区域,n=2、 3、 4时为环形区域), 并且L4=Lg,W4=Wg;txn-1和tyn-1(n=2, 3, 4)分别为两区域之间x和y方向的扩展尺寸。
不同石墨烯体积含量情况下, 考虑界面脱粘的5种工况, 如表7所示。在这5种工况下石墨烯/环氧树脂纳米复合材料杨氏模量Ecx的计算结果如图11所示。

表7 界面脱粘的5种工况
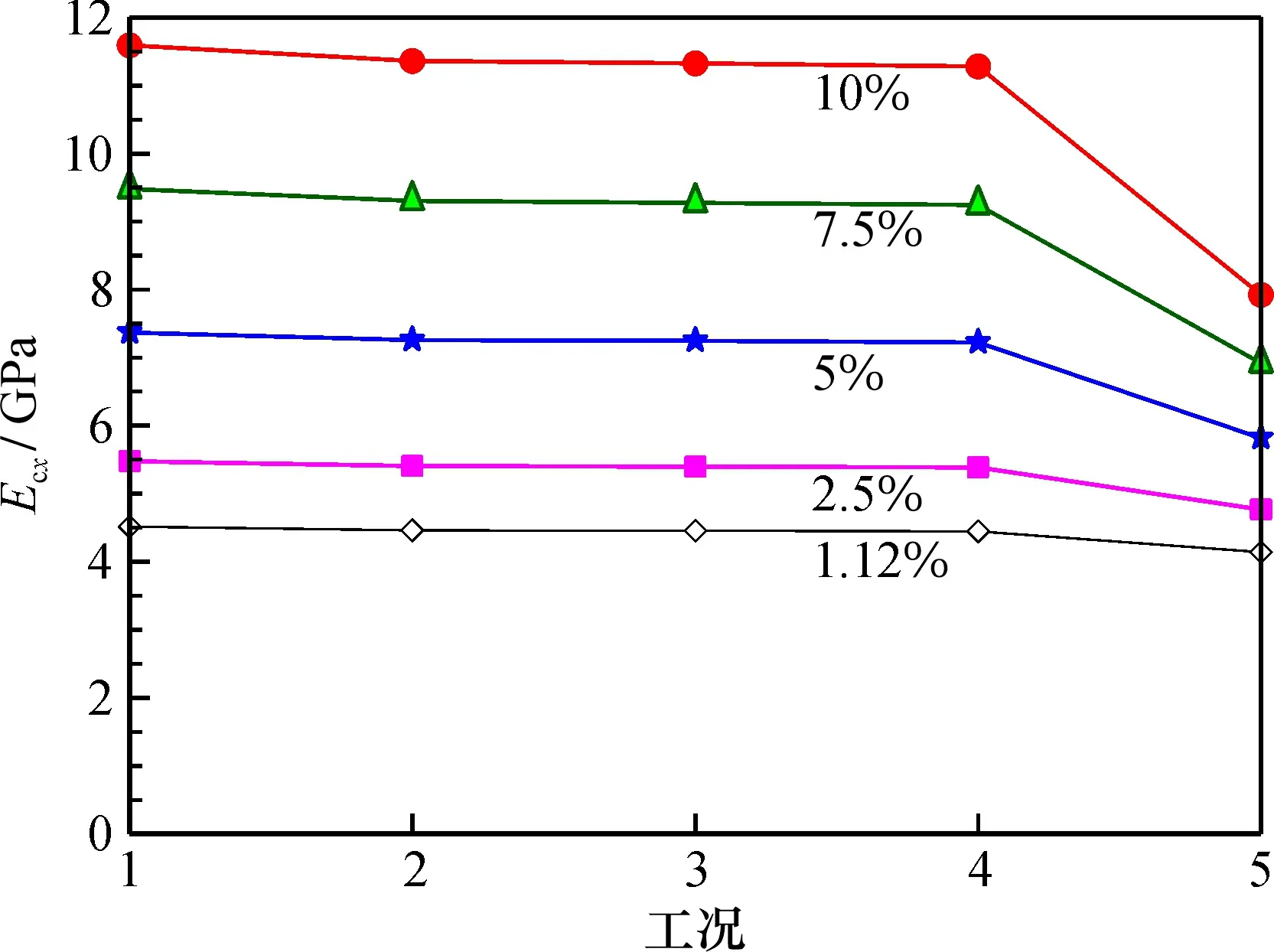
图11 不同石墨烯体积含量下区域脱粘对杨氏模量的影响
不同石墨烯体积含量情况下, 工况1(界面没有脱粘的理想情况)的石墨烯/环氧树脂纳米复合材料杨氏模量值最大, 而工况2、 3、 4、 5(界面不同区域发生脱粘)均会降低复合材料的杨氏模量。工况2(1区域脱粘)对杨氏模量的影响最小, 与界面没有脱粘的理想情况相比, 杨氏模量下降均在2%以内, 原因在于该区域位于界面的几何中心区, 此区域内结点的相对位移较小, 应力传递作用较弱; 工况5(4区域脱粘)对杨氏模量的影响最大, 各种石墨烯体积含量下, 杨氏模量的值都有较大的下降, 其中石墨烯体积含量为2.5%时, 对应的杨氏模量值下降了13%; 含量为10%时降低了32%, 原因在于该区域靠近石墨烯片的边缘位置, 此处石墨烯与环氧树脂基体的相对位移最大, 应力传递达到峰值。
综上所述, 在石墨烯与环氧树脂基体的粘结界面几何中心区域脱粘对纳米复合材料杨氏模量的影响最小, 靠近石墨烯片边缘位置的脱粘对该方向的杨氏模量影响最大。
4 结 论
本文通过有限元软件ABAQUS建模, 对石墨烯/环氧树脂纳米复合材料的弹性性能进行预测, 分析了界面约束以及界面脱粘区域对纳米复合材料弹性性能的影响, 得到如下结论:
(1) 在有限元软件ABAQUS建模中, 分别采用嵌入区域约束、 强绑定约束和弱绑定约束模拟石墨烯和环氧树脂之间界面的粘结作用, 据此得到纳米复合材料的杨氏模量值均比Halpin-Tsai理论模型的结果小, 最大偏差在4%以内, 并且嵌入区域约束比强绑定约束和弱绑定约束的结果更接近Halpin-Tsai理论模型的结果。
(2) 随石墨烯体积含量增大, 嵌入区域约束、 强绑定约束和弱绑定约束等3种模型计算的纳米复合材料的弹性性能均呈现线性增长的趋势。当石墨烯体积含量达到10.0%时, 有限元计算的纳米复合材料杨氏模量提高到环氧树脂的3倍以上。然而, 由于石墨烯材料具有团聚性, 可以预见石墨烯体积含量比较高时, 实际的增强效果没有达到模拟计算的增强效果。
(3) 石墨烯与环氧树脂之间的界面中心区域的粘结作用对纳米复合材料杨氏模量的影响最小, 边缘区域的粘结作用对纳米复合材料杨氏模量的影响最大。通过回字型脱粘的有限元分析, 得到了同样的结果, 验证了本文提出的有限元数值模拟方法的合理性。
