不同反演参数对高密度电阻率二维反演结果的影响

郭 鹏, 刘海飞, 刘声凯, 柳建新, 张一凡, 李昶萱

(1.中南大学 a.地球科学与信息物理学院; b.有色资源与地质灾害探查湖南省重点实验室, 长沙 410083;2.湖南省水文地质环境地质调查监测所, 长沙 410129)

0 引 言

高密度电法具有数据采集高效、 涵盖信息量大等优点, 已被广泛应用于水文、 工程和环境等领域, 并且在地下水资源、 岩溶、 滑坡、 采空区、 隐伏构造及污染场地监测等方面均得到了较好的应用[1-8]。二维反演作为高密度电法数据处理的重要技术手段, 在很大程度上影响了高密度电法的勘探效果。对高密度电阻率数据反演之前需要设定反演参数, 不同的反演参数对应得到的反演结果常常存在差别, 因此如何根据观测装置、 数据质量等因素选取合理的反演参数显得尤为重要。目前针对反演参数的选取问题已有相关研究, 黄真萍等[9]通过数值试验研究了高密度反演的最佳深度转化因子; 柳建新等[10]讨论了正则化参数对反演结果分辨率和反演稳定性的影响; 余长恒等[11]讨论了反演过程中阻尼系数和正演网格大小对突出异常体的作用。

为全面分析反演参数对反演结果的影响, 结合文献[12-13], 本课题组编写了高密度电阻率二维反演程序, 对高密度电阻率二维反演参数的选取问题展开试验研究。通过设置不同的反演参数, 包括正反演网格大小、 先验约束条件、 雅可比矩阵计算方法、 目标函数的范数、 反演迭代次数、 初始阻尼因子、 初始模型等, 对比分析不同参数对电阻率二维反演结果的影响, 并针对装置和数据特点总结出反演参数的优化选择, 可以为高密度电阻率二维反演处理提供参考。

1 高密度电阻率法二维正反演基本原理

1.1 高密度电阻率二维正演

高密度电法的二维正演问题归结为求解波数域点源稳定电流场的边值问题

(1)

其中:V为波数域电位;λ为波数;σ为电导率; 点源项f=-Iδ(A)/2;C=K1(λR)cos(R,n)/K0(λR),K0和K1分别为第二类0阶和1阶修正贝塞尔函数。

利用泛函分析将波数域点源稳定电流场的边值问题(式(1))转化为等价的变分问题

(2)

采用有限元法求解变分方程(2)[14], 可将变分问题转化为线性方程组

KV=f,

(3)

其中：K为对称稀疏数矩阵;V为网格节点处波数域电位构成的列向量。

利用一维变带宽存储矩阵, 并用乔里斯基分解法求解方程, 即可得到波数域电位V, 然后通过傅氏逆变换将波数域电位转换到空间域电位

(4)

其中:Wi是与波数λi对应的傅氏逆变换权系数;k为波数个数。最后根据观测装置将电位U转化为视电阻率。

1.2 高密度电阻率二维反演

对数据空间和模型空间在混合范数下构建目标函数[15-16]

(5)

其中:da为实测数据;dc(m)为模拟数据;m为地电模型;mb为背景模型;C为光滑度矩阵;λ为阻尼因子;p和q为范数阶, 通常取为1或2。

式(5)两端对m求导并令其为0, 得

(6)

然后, 将dc(m)在初始模型m0处泰勒级数展开, 并略去二次以上的高次项, 得

=dc(m0)+A(m-m0),

(7)

其中,A为偏导数矩阵。将方程(7)代入方程(6), 得到混合范数下的线性反演方程

λ·CTRmC(m-mb),

(8)

其中： Δd=da-dc(m0)为数据残差向量; Δm=m-m0为模型修正量;Rd=|Δd-AΔm|p-2为数据加权矩阵;Rm=|C(m-mb)|q-2为模型加权矩阵。

利用共轭梯度法求解线性方程组(8), 即可得到模型参数修正量Δm, 再将其代入公式

m(k+1)=m(k)+Δm,

(9)

便得到新的地电模型, 重复上述迭代过程, 直到满足反演终止条件为止。

2 反演参数的设计方法

以下分别对正反演网格剖分、 目标函数的范数、 初始模型、 偏导数矩阵的结合方式、 反演迭代次数、 先验约束方式、 阻尼因子等参数的设计方法进行分析讨论。

2.1 正反演网格剖分方法

在高密度电法反演时, 研究区域的网格剖分将涉及横向网格剖分、 纵向网格剖分、 反演深度, 其中横向网格剖分通过横向单位电极距剖分的网格数调整, 纵向网格剖分由纵向首层网格厚度、 纵向层厚随深度增加的递增系数调整, 具体为:

横向正演网格:ehs=a/c,

其中:c=1, 2, 3, 4;a为相邻电极间距。

横向反演网格:ehm=ehs×h,h=1,2,3,4。

纵向正演和反演网格: 纵向正、 反演网格单元厚度一致, 网格尺度采用逐渐递增方式

evs(i)=evm(i)=evs(i-1)×f,i=1,2,…,n。

(10)

其中:f∈[1.1, 2]为层厚度调整系数;evs(0)=a×g为纵向首层网格厚度;g∈[0.1, 0.5]为首层网格调整系数。

反演深度:D=k×ABmax/2,

其中:ABmax/2为最大视深度;k∈[0.25, 0.8]为深度调整系数。

2.2 目标函数的范数

根据线性反演方程(8), 可以采用4种方式构建目标函数, 即： ①数据空间p和模型空间q均为2范数; ②数据空间p为2范数, 模型空间q为1范数; ③数据空间p为1范数, 模型空间q为2范数; ④数据空间p和模型空间q均为1范数。

图1 正演网格示意图

2.3 初始模型

由于广义线性反演结果很大程度上受初始模型影响, 在高密度电阻率二维反演时, 可以给定均匀或非均匀初始模型(标识IM=0为均匀,IM=1非均匀)。

对于均匀模型, 可将实测数据取平均值作为初始模型, 即

(11)

其中：ρai为实测视电阻率,i=1, 2, …,n；n为数据个数。

对于非均匀初始模型, 可利用反距离加权插值公式

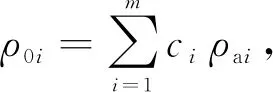
(12)

根据实测数据的视记录点对地下模型进行二维插值, 其中di为已知点到待插点的距离,m为选取的临近数据点的个数。

2.4 阻尼因子

误差收敛曲线通常在前几次迭代下降较快而后缓慢下降, 考虑采用函数

λ(k)=a·k-2+b

(13)

构造阻尼λ序列。其中:k为迭代序号;a和b为待求系数。首先给定反演迭代次数nmax, 并根据数据所含噪音情况选择相对合理的初始阻尼λmax(通常在0.1～1内选择), 为方便起见, 设最小阻尼为λmin=λmax/10, 这样即可确定a、b。若取nmax=5,λmax=0.5,λmin=0.05, 则根据式(13)可得λ序列为0.5、 0.152 9、 0.089、 0.066、 0.056、 0.05。

2.5 反演迭代次数

选取反演迭代次数nmax(如5～15)作为反演的终止条件, 若仅以拟合差作为终止条件， 实际中有时难以满足。

2.6 先验约束

为减少反演产生的假异常, 反演时需要对模型空间施加先验约束, 主要包括光滑约束SC(选择0或1)和背景约束BC(选择0或1)。

2.7 偏导数矩阵的结合方式

在高密度电阻率反演中, 常采用以下两种计算偏导数矩阵的方法。

①互换原理: 视电阻率对模拟电阻率的偏导数计算可以归结为网格节点电位对模拟电阻率的偏导数计算。互换原理表明, 在某节点iA供电时jM点的电位等价于在jM点供电时iA点的电位, ∂V/∂ρ为所有网格节点的电位的线性组合, 经过变换求出偏导数矩阵。

②拟牛顿法: 采用Broyden秩一校正公式近似计算雅可比矩阵

(14)

其中：Bk为第k次迭代的雅可比矩阵;sk为第k次迭代模型参数的改正量;yk为第k次和第k+1次迭代模拟视电阻率的差。

拟牛顿法计算偏导数矩阵的效率远远高于互换原理法, 本文将两者结合起来, 即前nc次迭代采用互换原理, 后nb=nmax-nc次迭代采用拟牛顿法, 在保证不降低分辨率的情况下提高反演速度。

3 反演试验结果分析

3.1 反演试验断面介绍

选取两种高密度电阻率法观测装置的实测断面作为试验断面。试验断面一为浙江某地温纳Beta装置采集的高密度电阻率数据(图2a), 点距2 m, 电极60个, 测点570个, 最大视深度为56 m, 测线地形起伏。根据已知地质信息, 该地区的地质情况为: 里程0～50 m主要以砂页岩为主, 里程75～85 m主要以灰岩为主, 里程90～100 m、 深10～20 m处存在溶洞。

试验断面二为湖南某地温纳施伦贝尔装置采集的高密度电阻率数据(图2b), 点距5 m, 电极60个, 测点722个, 测线地形水平。已有钻孔资料显示: 在730 m处0～9.8 m为黏土, 9.8～15.2 m为白云质灰岩, 15.2～18.6 m为含砾长黏土, 18.6～72.8 m为白云质灰岩, 其中67.3～73.6 m为溶洞。

3.2 不同反演参数对反演结果的影响分析

3.2.1 正反演网格 采用试验断面一作为测试对象, 反演时只改变纵向网格剖分参数, 其他反演参数如表1所示。通过增大层厚度调整系数f, 正演网格尺寸增大, 深部的分辨率略有降低, 但不影响异常位置, 网格越小均方差越小且收敛速度快, 耗时长(图3a—c); 通过增大深度调整系数k, 反演深度越大, 越能反映深层电阻率情况以解决边界问题, 但耗时长(图3d—f), 如果超出测深范围, 易造成虚假异常(此处f、k对应2.1节所述, 下文相同)。采用稀疏网格反演耗时短, 可压制噪声; 精细网格降低围岩对异常体的影响, 有利于分辨异常界面, 突出自身异常。

表1 设置不同正反演网格剖分参数时的参数设置

图3 改变纵向网格调整系数时试验断面一的反演结果

3.2.2 混合范数 反演时数据空间和模型空间选取不同的范数组合构建目标函数, 其他反演参数设置如表2所示。对试验断面一进行反演试算, 反演结果如图4所示。不同范数组合的反演结果形态类似, 仅局部区域存在少量差异： 数据空间选择1范数时, 突出浅部高阻, 模型空间选择1范数时, 深部低阻范围大； 当数据空间和模型空间均选择2范数时, 限制了深部低阻范围, 压制了浅部高阻。范数的选择主要与数据噪声的分布规律, 即高斯分布或正态分布有关。

图4 数据空间与模型空间采用不同范数组合时试验断面一的反演结果

表2 改变范数组合反演时的参数设置

3.2.3 初始模型 反演时分别选取均匀和非均匀初始模型对试验断面二进行反演试算, 其他反演参数设置见表3。具体反演结果如图5所示, 反演结果对初始模型的依赖性较大, 均匀初始模型的反演结果不能反映出溶洞的存在(图5a), 而非均匀初始模型的反演结果能较好地反映异常体的存在。对于拟断面图中深部显示的弱异常信息, 通过给定较优的初始模型可以提高反演结果的分辨率。

图5 采用不同初始模型时试验断面二的反演结果

表3 给定不同初始模型反演时的参数设置

3.2.4 阻尼因子 对试验断面二选取不同的阻尼因子进行反演试算, 其他反演参数设置见表4。初始阻尼因子分别选取0.1和0.5时反演结果分别如图6a、 6b所示, 反演结果受阻尼因子的影响较大： 初始阻尼因子为0.1时， 深部溶洞异常在反演剖面中得到较好的体现； 而初始阻尼因子为0.5时， 深部溶洞异常已被平滑掉。实际中由于数据所含噪声通常不同, 很难根据噪声水平选取能使模型得到最佳分辨又可使误差收敛曲线稳步下降的最佳阻尼因子, 但可以通过给定不同的阻尼因子进行反演试验, 从中选取符合地质规律的反演结果。

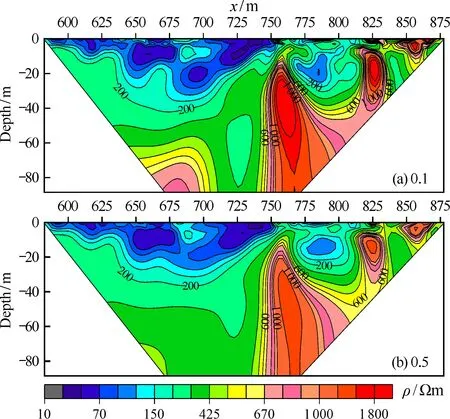
图6 设置不同阻尼因子时试验断面二的反演结果

3.2.5 反演迭代次数 对试验断面二选取不同的迭代次数进行反演试算, 其他反演参数设置见表5。迭代4次和8次的反演结果分别如图7a、 7b所示, 当反演迭代4次时(耗时60 s), 溶洞未能反映出来, 当迭代至8次时(耗时87 s), 溶洞已得到较好的分辨。因此, 反演迭代次数也是影响反演结果的一个因素, 迭代次数不足, 反演结果可能未达到最佳逼近, 迭代次数过多, 会增加反演耗时, 实际中反演迭代6～10次误差收敛曲线已基本趋于稳定。

表5 改变反演迭代次数时的参数设置

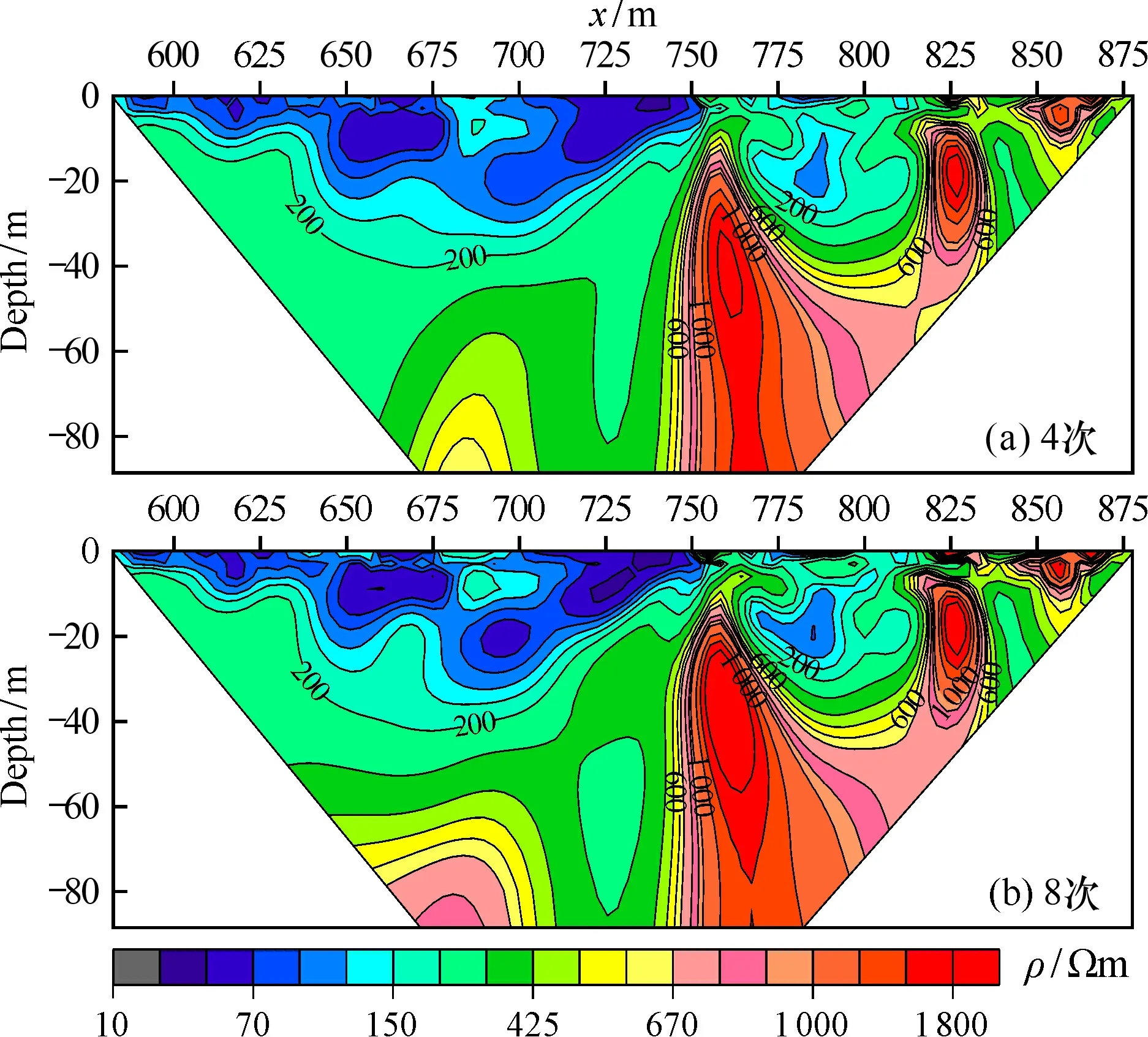
图7 设置不同迭代次数时试验断面二的反演结果

3.2.6 先验约束 对试验断面二选取不同的先验约束进行反演试算, 其他反演参数设置见表6。施加背景约束和同时施加光滑与背景约束的反演结果分别如图8a、 8b所示, 两者反演异常形态大致类似, 仅施加背景约束时电阻率等值线多呈锯齿状, 而同时施加光滑与背景约束时电阻率等值线较光滑。实际中选取背景约束更能凸显弱异常信息, 而对于强异常信息同时施加背景和光滑约束的反演异常等值线将更为平滑流畅。

表6 改变先验约束反演时的参数设置

图8 采用不同先验约束时试验断面二的反演结果

3.2.7 互换原理与拟牛顿法结合计算雅可比矩阵 采用互换原理和拟牛顿法相结合的方式计算偏导数矩阵, 当反演迭代次数设置为6次时, 改变互换原理和拟牛顿法使用的次数, 其他反演参数设置见表7, 对试验断面一进行反演试算, 结果分别如图9a、 9b所示。随着互换原理计算雅可比矩阵次数的增加, 断面异常形态无明显变化, 互换原理使用3次时反演耗时72 s, 互换原理使用5次时反演耗时132 s。这说明在电阻率二维反演中, 互换原理计算偏导数矩阵比较耗时, 而拟牛顿法则比较节省时间, 尝试将互换原理与拟牛顿法结合计算偏导数矩阵。考虑到反演迭代误差收敛曲线通常仅前2～3次收敛较快, 在后续迭代中收敛曲线下降缓慢。因此, 可将前2～3次迭代采用互换原理法后续迭代采用拟牛顿法计算偏导数矩阵, 在保证反演稳定和分辨率的情况下加快反演计算速度。

表7 采用不同方式计算偏导数矩阵时的反演参数设置

图9 互换原理与拟牛顿法结合时试验断面一的反演结果

4 结 论

(1)通过对不同反演参数进行反演试验, 正反演网格大小应根据装置特点选择, 偶极装置横向分辨率高, 可设置横向正反演网格为点距的一半或更小; 温施装置探测深度大, 设置纵向反演网格深度尽量大于最大视深度的一半。通常情况下, 横向正反演单元设置为点距的一半, 纵向首层网格单元设置为点距的0.2倍, 纵向网格调整系数设置为1.2, 纵向反演网格深度调整系数在很大程度上取决于最大视深度AB/2和地层电性, 电性值越低深度调整系数越小, 反之越大, 一般情况下设置为0.5, 必要时加大。

(2)初始模型和阻尼因子在很大程度上影响反演结果的分辨率, 如果异常信息较弱, 则选择非均匀初始模型和较小的初始阻尼因子。

(3)当数据噪声较小且服从拉普拉斯分布, 数据空间和模型空间均选择2范数, 反之当数据噪声较大且服从高斯分布时, 数据空间或模型空间选择L1范数; 对于其他反演参数, 通常设置为同时施加光滑和背景约束、 反演迭代次数为6(前两次迭代采用互换原理、 后4次迭代采用拟牛顿法计算偏导数矩阵)。

(4)在处理和解释实测高密度电法数据时, 选择合适反演参数能够提高反演效率和反演结果的准确性, 讨论高密度电法二维反演参数是非常有必要的。实际中对于较为复杂的地质问题, 需要反复调整各参数进行反演试验, 从中选取符合地质规律的反演结果。