高陡顺层边坡动态强度折减法研究

谢志辉 古松

（中交三公局第一工程有限公司 北京 100012）

1 工程概况

本项目巴马—凭祥公路巴马至田东段工程主线深路堑以碎屑岩（砂岩）边坡为主，共有深路堑23 处边坡，坡面走向与岩层走向相近，边坡开挖角度大于岩层倾角（顺层坡）。本地区属剥蚀低山丘陵地貌，地形起伏较大，自然坡度约20°。边坡表层具有第四系粉质黏土所覆盖，含较多碎石，厚度大致在0.6～0.9m。以下基岩主要组成是三叠系中统百逢组地层，岩性为黄褐色砂岩，中厚层状构造，强～中风化为主，岩块硬、脆，岩体相对破碎，强风化层厚约6～11m，岩层产状为55°/NW∠45°，此类边坡易发生沿层面的顺层滑动［1］。结合YK8+110～YK8+380段碎屑岩边坡滑坡，分析高陡边坡动态强度折减法的可行性。

本文主要以折减范围作为计算重点，采用并检验了动态强度折减方法针对边坡滑坡过程进行研究计算，利用山体和土体的定量损伤评估指数来检查坡体的局部损伤面积。在折减计算阶段，将一些力参数控制在局部破坏区域内，促使边坡逐步持续破坏，在这个过程中自动搜索潜在的滑动面。实践得到，在此采取的动态强度折减法［2］能够达到模拟边坡的渐进破坏过程的工程目标，为强度折减法提供了一种新的计算方法，可以更有效地评估边坡稳定性。

2 动态强度折减计算

2.1 动态强度折减计算原理

动态强度折减法广义上来说是局部折减法和整体强度折减法的总结，用来表达边坡从局部到整体的失稳的基本过程。动态强度折减法在这里应用的目标是使渐进失稳过程科学地显化，整体强度折减法用于确定安全系数，所以，这里认为动态强度折减算出的滑动范围满足工程要求。因此，在计算时，首先进行整体强度折减试算，通过试算，确定出这个滑带的不稳定区域土体单元，再进行这部分土体单元黏聚力和内摩擦角的折减。

2.2 动态强度折减计算特点

边坡岩土体是非均质性的，边坡破坏先从局部薄弱位置开始，随后逐步向其他方向发展。为了确定边坡怎么样从局部到整体逐步失稳破坏这个连续过程，采用了动态强度折减的计算方法，这种方法具有以下方面的特点［3］。

（1）折减过程数据动态变化。在折减过程中，其破坏范围从小部分发展至全体动态扩展，可以反映边坡渐进破坏过程。

（2）自动显示渐进滑动面。利用折减过程持续不断地扩展，这个过程中会搜索出边坡失稳的不稳定关键区所在，显示出滑坡的大致滑动面。

动态强度折减计算程序如图1所示。

图1 动态强度折减计算

2.3 动态强度折减计算过程

首先，通过对各边坡单元的强度参数进行折减，过程中致使软弱边坡单元损伤；然后，下一步继续折减这部分损伤单元，同时，弹塑性力学的相关平衡计算也要进行，坡体破损区域在这个过程中将明显扩大［4］。后续强度折减法计算中，以新的破损区域内的参数按照新的折减系数再次继续折减，采用局部边坡单元强度参数的折减法及对损伤区坡体的坡度持续不断增大，直至达到极限平衡状态。

动态折减法［5］的最终目标是为了确定折减范围，这也说明边坡体危险区域在破坏过程中将会一直显现出来并持续不断扩展，所以，在边坡渐进失稳这个过程中，对于这个破损区域的确定将是整个问题的难点。这里采用屈服接近度YAI这一物理参数来达到解决问题的目的，之后，采用动态强度折减计算得到最后的破损区域，以Mohr-Coulomb为准则的YAI计算公式为：

YAI的取值范围是［0，1］，在公式中，当YAI=0时，其物理意义是应力点达到屈服状态；当YAI=1时，意味着边坡是最安全稳定的状态。

专家学者通过各自试验发现，岩土体在的加载过程中存在一个屈服范围，其中，岩体开裂的对应应力阈值大约在峰值强度的80%，这里为确保应力值在阈值内，因此，选取80%的底限阈值去计算确定折减破损区范围，对应的YAI＜0.2的区域将被定义为破损区。需要主要说明，本文中所提到的边坡破损区是公式计算得到的边坡塑性区（YAI=0）及损伤区（0＜YAI＜0.2）之和，其物理意义表现为坡体破损区应大于屈服破坏区。

3 边坡渐进破坏

3.1 边坡渐进破坏原理

根据边坡相对应的坡体参数和边界范围条件，建立了相应的数学模型。考虑到新的损伤区是由初始局部力S2减小得到的，而新的损伤区是由初始局部力Si+1减小得到的（Si+1是最新的断裂带），在断裂带等处给出了Si+1，K2的还原系数，因此，K（K1，K2，K）避免了在限位区与非限位区交界处由于土体力学参数跳变而造成的不符合实际的区域。用实验方法确定了各计算步骤K值的增量，每一步K值的增加都会直观地反映裂缝面积的增加，如果K值的增加较大，则下一步裂缝面积的增加相对较大，但对边坡最终破坏时K值的确定没有明显影响。因此，在损伤计算的早期阶段，可以大幅度提高损伤计算的实用性，当损伤敏感区较迟时，可以使用更精确的增量来获得更精确的结果。

根据不同的强度折减系数和有限元计算结果，可以减小不同阶段的断裂带。随着计算的进行，边坡体局部损伤区K值不断增大，并不断向上扩展，边坡表面潜在滑动面逐渐显现，最终从在塑性区形成过程中完成了边坡渐进破坏模拟。

3.2 边坡渐进破坏计算步骤

根据边坡渐进破坏显示的力学特点和动态强度折减法计算原理，在此基础上，建立了模拟具体边坡渐进破坏过程的数学计算方法。其具体步骤如图2所示。

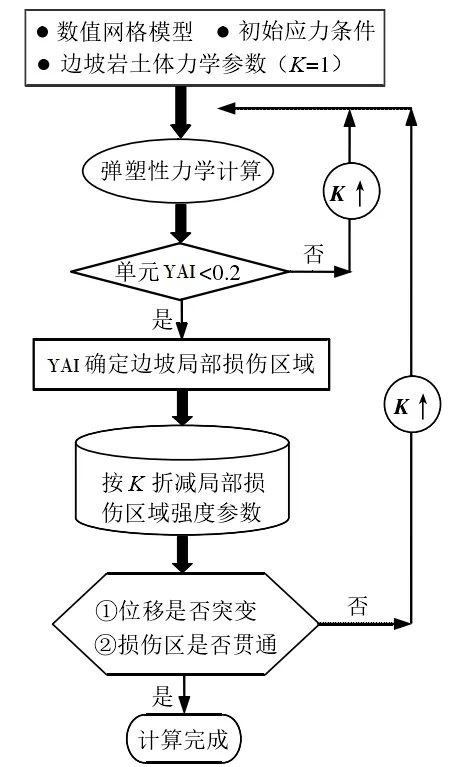
图2 基于动态强度折减法的边坡渐进失稳模拟

（1）首先，确定地质地貌、岩土力学参数、应力场等，为动态极限方法的计算确定基本的假定初始条件，并在此基础上建立相应的数值模型。

（2）在K=1的情况下，采用弹塑性力学方法计算边坡的屈服接近指数，判断边坡是否存在单元损伤（J＜0.2），若无单元损伤，则K的折减系数不断增大，对边坡局部损伤单元进行弹塑性力学计算。

（3）本文用YJ 指数确定边坡的渐进破坏区，将破坏区的强度参数K减为极限模量K，然后用极限模量代替极限弹塑性计算程序进行计算。

（4）根据图1所示的动力极限计算程序，随着极限模量的不断增大，边坡的破坏面积不断扩大，最终形成边坡的滑动面，边坡的承载力岩土自身稳定性将继续下降。

（5）折减计算最后一部分，根据所得数据绘制边坡的软弱部分监测点位移和折减次数的关系曲线图，依据位移和折减次数相关关系曲线，得到位移突变点的发生位置。研究发现，该位置边坡变形从初始的匀速变形逐步过渡到加速变形，可命突变点所对应的位移数据当作边坡稳定性评价标准和边坡滑动预警的依据［6］。

4 结算结果比较

4.1 动态强度折减计算结果

在整体强度折减计算中，边坡体的塑性区不仅被夸大，而且在边坡体的深度处也经常出现塑性区。动态折减法可以求出边坡稳定面上的断裂带和滑动面，避免了整体强度折减法影响面过大的缺点。由于积分强度折减法不能求出滑动面在断裂带内的位置，因此，滑动面的位置往往是由剪应力增量决定的。目前尚无统一的选择剪应力增量的标准，需要通过调整剪应力增量的值来获得。本文以动态强度折减法来直接获得滑动面，滑动面的位置和形状也能够直接由破坏区来确定。

局部折减法根据相关文献［7］减小了滑动面的力学参数。在前15次折减（即通过滑动面），动力位移折减值为11mm，局部位移折减值为12.5mm，整体位移折减值为14mm。利用局部强度折减法，证明了实际高陡顺层岩质边坡强度折减法所得数据大小顺序依次为：整体强度折减＞局部强度折减＞动态强度折减。

4.2 动态强度折减优越性

强度折减法在边坡稳定性分析中得到了广泛的应用，它不仅得到了一个稳定的安全系数，还降低了边坡的各项强度参数，因此所得计算数据相比实际数据较大。边坡的变形破坏是一个从破坏的内坡面逐渐滑动到整个滑动面的渐进过程，因此，传统的强度折减法不能反映边坡的动力失稳过程。相对而言，动态强度折减法可以很好地解决相关的顾虑。

对于非均质的层状岩体坡，仅通过对各层面岩体土强度的单一折减，不能得到反映实际现状的应力参数和安全系数［8］。本文所研究的动态强度折减法可以相对较好地模拟非均质边坡的演化致灾过程。动态强度折减法在非均质边坡中更有实用意义和科学依据，因为其合理地说明了非均质边坡中的弱部单元将先受到破坏，然后渐渐地发生演化和扩展，使边坡在局部薄弱区长度动力强度折减法在古滑坡、节理岩质边坡、断层等非均质边坡的稳定性评价中将发挥越来越重要的作用。

本文分别用两种方法对I-I 模型进行了分析。本文将研究区的力学参数引入模型，在自然条件下，通过减小模型的内聚力和内耗角最后给出了仿真结果。通过研究可以看出，无论是静态还原还是动态还原，随着还原次数的增加，塑性区都在不断扩大。但是，积分法得到的塑性区非常大，包括整个上盖层，与实际情况有很大差距。研究区第二层岩石中泥岩的塑性区与实际情况较为吻合，能较好地反映岩石的塑性变形特征。综合以上内容，研究区边坡的实际失稳危险范围及潜在滑动面采用动态强度折减可取得较好结果。

5 结语

本文采用局部强度折减法对边坡的强度折减过程进行了数值模拟，结果表明，边坡的破坏区首先出现在边坡的底部和内部。此外，该方法能有效地控制大面积边坡的内部损伤，使边坡渐进破坏模拟更符合实际失稳过程。通过对影响区发展过程的详细记录和深入分析，得出影响区边坡是导致边坡后期加速破坏的主要因素。在边坡破坏过程中，采用分步局部强度折减法，可以保证边坡破坏过程的梯度，平均将极限区与非极限区的塑性应变差减小40%。为了解决滑动面上塑性应变值的跳跃问题，采用统一的方法来减小局部力，保持塑性区的连续性变化，模拟边坡的破坏过程。

通过动态地降低局部损伤边坡的强度参数，使其逐渐演化为贯通孔的滑动面，真实再现了边坡潜在滑动面的形成过程克服了各种强度折减方法的影响。动态强度折减法可以直接求出边坡损伤区的滑动面，克服了缺乏统一的剪应变增量准则的缺点。动力强度折减法能有效地解决一系列的折减法问题，是对强度折减法的改进和发展，为边坡稳定性的全过程模拟和定量评价铺平了道路。