基于层次分析法的居民拆迁安置小区建设综合评价研究

徐 陶，徐超毅

(安徽理工大学 经济与管理学院，安徽 淮南 232001)

拆迁老旧小区，群众生活安置工作是工程实施建设的基础和前提，但若因处理不当，极易引发社会矛盾和纠纷，给政策推进落实造成一定的困难，因此征地拆迁、新建安置小区既关系着政府战略的实施和城市基础设施建设的顺利推进，也关系着群众的切身利益。影响房屋拆迁的因素很多，如城市建设总体规划、人均纯收入、拆迁安置地点选择、拆迁补偿方式、拆迁补偿标准等。基于多种因素的影响，运用层次分析法对各个影响因素的权重进行排序，对影响因素的重要程度进行划分，有针对性地提出应对拆迁问题的办法，从而提高人们对拆迁安置工作的认可度和满意度，为政府提供一种较为合理的综合分析评价方法，有力推动城镇化的高质量发展。

1 基于AHP的城市居民拆迁安置小区影响因素重要性的研究

1.1 AHP基本原理

层次分析法(Analytic Hierarchy Process，简称AHP)是美国运筹学教授T.L.Saaty于20世纪70年代初提出的，它是对定性问题进行定量分析的一种系统、简洁、高效、实用且所需定量信息较少的多准则决策方法。该方法自1982年引入我国以来，迅速在国内经济社会各个领域得到了广泛重视和应用。层次分析法是在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息令决策思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。

层次分析法是根据问题的性质和要达到的总目标，将问题中的各个因素按总目标、各层子目标、评价准则，划分成为互相关联影响和隶属关系的有序的层次结构，从而形成一个多层次的分析结构模型，根据对一定客观事实的主观判断结构，将专家意见和分析者客观判断结果直接有效结合起来，把一层次中元素两两比较得到的重要性进行定量描述，再利用求解判断矩阵特征向量的办法计算出反映每一个层次元素的相对重要性次序的权值，对所有层次之间的总排序进行计算，得出所有元素的相对权重并进行排序。

1.2 层次分析法及其基本步骤

层次分析法的基本思路是找出影响评估问题的所有主要因素，将这些因素按评估目标、评估准则(属性)和备选方案等层次分类。通过构造一个反映各因素关联隶属关系的递阶矩阵模型，把一个复杂决策问题表示为有序的递阶层次结构，递阶层次包括目标层、准则层和方案层三个基本层次，准则层可以继续细分为下一级子准则，再通过每一层各因素对其上一层因素影响的两两相比较定量打分，得到各因素的相对重要性排序，最后按层次结构关系得到对评估问题的各备选方案的综合打分排序[1]。

分析系统中各因素间的关系，建立系统的递阶层次结构模型；对同一层次的各元素关于上一层中某一准则的重要性进行两两比较，构造两两比较的判断矩阵；由判断矩阵计算被比较元素对于该准则的相对权重；层次单排序及一致性检验；层次总排序并进行一致性检验。

1.3 构建城市居民拆迁安置小区影响因素评价模型

本研究在广泛查阅相关文献，多次咨询政府人员、规划与设计院人员、待拆迁居民、物业管理人员、长期从事拆迁的一线工作人员及长期研究安置小区建设的专家学者的基础上，建立了安置小区影响因素综合评价体系。它由目标层、准则层、指标层构成，根据统计学相关理论，结合安置小区建设实际情况，初步选取4个一级指标，分别为拆迁安置方案、安置小区整体情况、房屋情况及整体环境，并由19个评价指标构成，基本能够覆盖对安置小区建设有影响的各个因素，得到了较为全面的评价。

1.4 基于AHP评价模型的数据分析

从目标层A开始，对隶属于目标层的下层因素采用两两比较法和1～9标度构造判断矩阵。

表1 居民拆迁安置小区建设影响因素评价体系Tab.1 Evaluation system of influencing factors of residential demolition and settlement community construction

表2 1～9标度的含义Tab.2 Implication of 1～9 scale

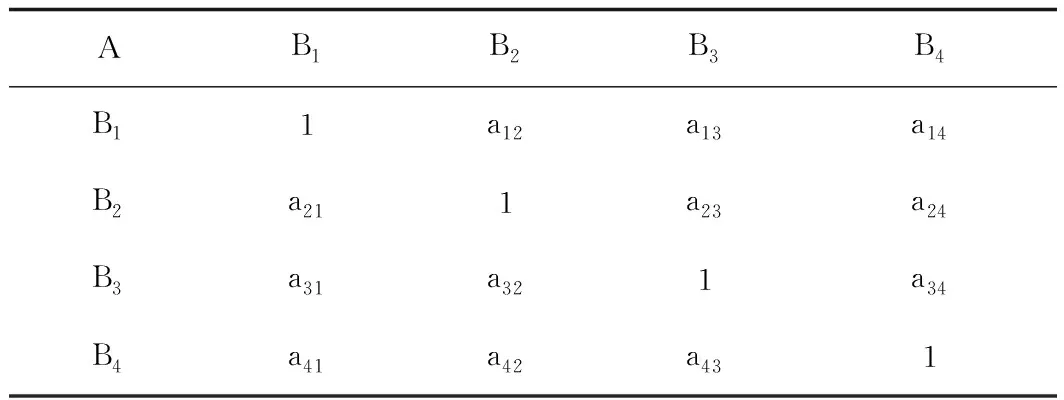
表3 两两比较判断矩阵Tab.3 Comparison of judgment matrix in pairs

1.5 影响房屋拆迁安置的因素

确定影响拆迁安置小区建设指标的权重值，运用层次分析法，通过两两比较确定层次中每一层相对于上一个层次某个因素的相对重要性，按照9级标度法进行赋值构造判断矩阵，根据判断矩阵对层次进行单排序及总排序，找到各因素指标的权重值，如表4所示。

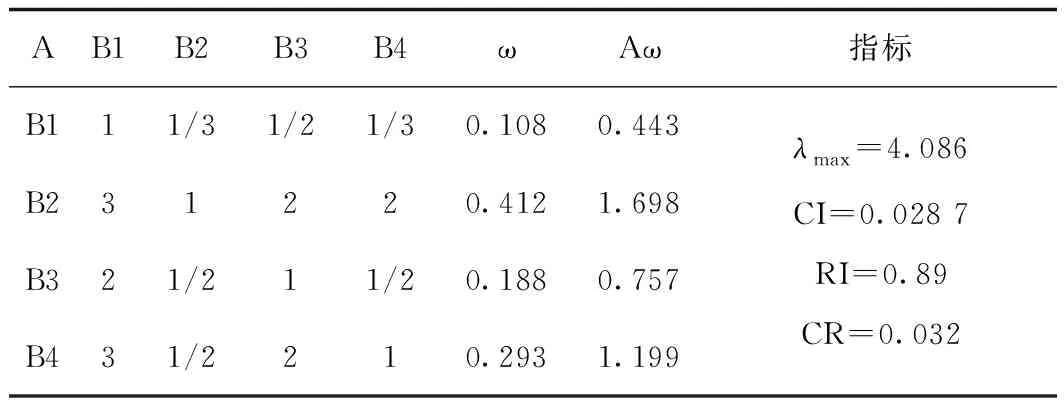
表4 判断矩阵A-BTab.4 Judgment matrix A-B

建立居民安置小区建设关注点的层次结构，构造判断矩阵，在建立了层次结构图以后，根据上下层因素之间的相对重要性，利用9级标度法进行赋值，从而建立判断矩阵(如表5～表8所示)。

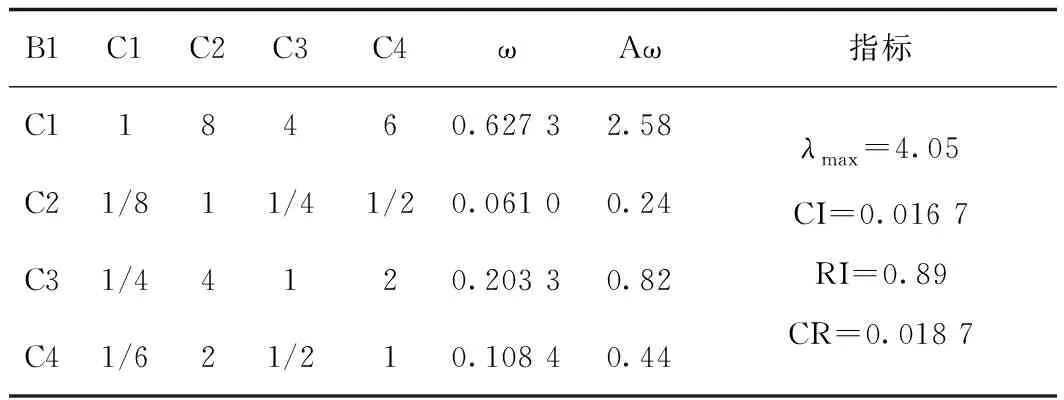
表5 判断矩阵B1-CTab.5 Judgment matrix B1-C

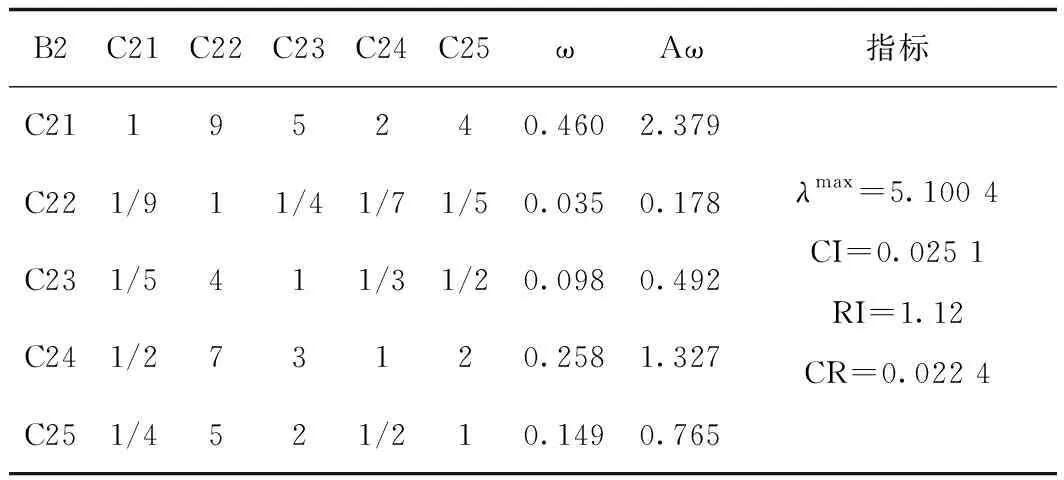
表6 判断矩阵B2-CTab.6 Judgment matrix B2-C

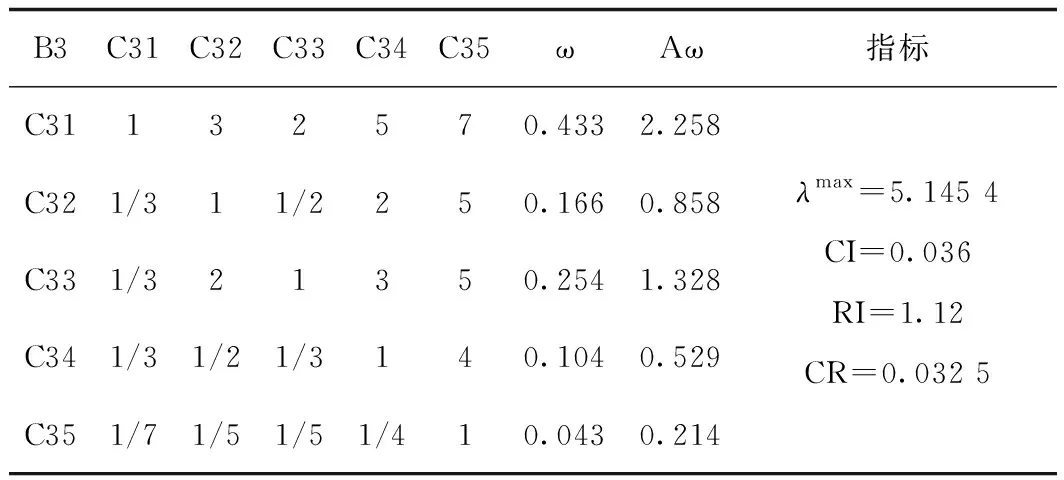
表7 判断矩阵B3-CTab.7 Judgment matrix B3-C

表8 判断矩阵B4-CTab.8 Judgment matrix B4-C

计算各层次中各因素指标的权重。利用和积法对上述判断矩阵分别计算出权重和最大特征根，由于判断矩阵的分值是由人为进行赋值的，因此可能存在不一致的情况，所以需要进行一致性检验。具体计算方法为：第一步：计算一致性指标CI：CI= (最大特征值-n)/n-1，其中， n表示判断矩阵的阶数。第二步：查询相应的平均随机一致性指标，如表9所示。第三步：计算相对一致性指标CR。CR=CI/RI。若CR<0.1，则认为该判断矩阵通过了一致性检验，若CR>0.1，则该判断矩阵需要修正。

表9 一致性指标RI查询表Tab.9 Query table of consistency indicator RI

层次总排序。如果要得出各个层次中所有元素对于总目标的相对重要性权重，需要对权重进行自上而下的排序，该判断矩阵的层次总排序结果如表10所示。

由表10可以看出，在居民安置小区建设关注点的因素指标中，质量是最重要的，其次是区位，再次是学区。因此，在安置小区建设过程中，政府应加大对安置小区质量的关注度。

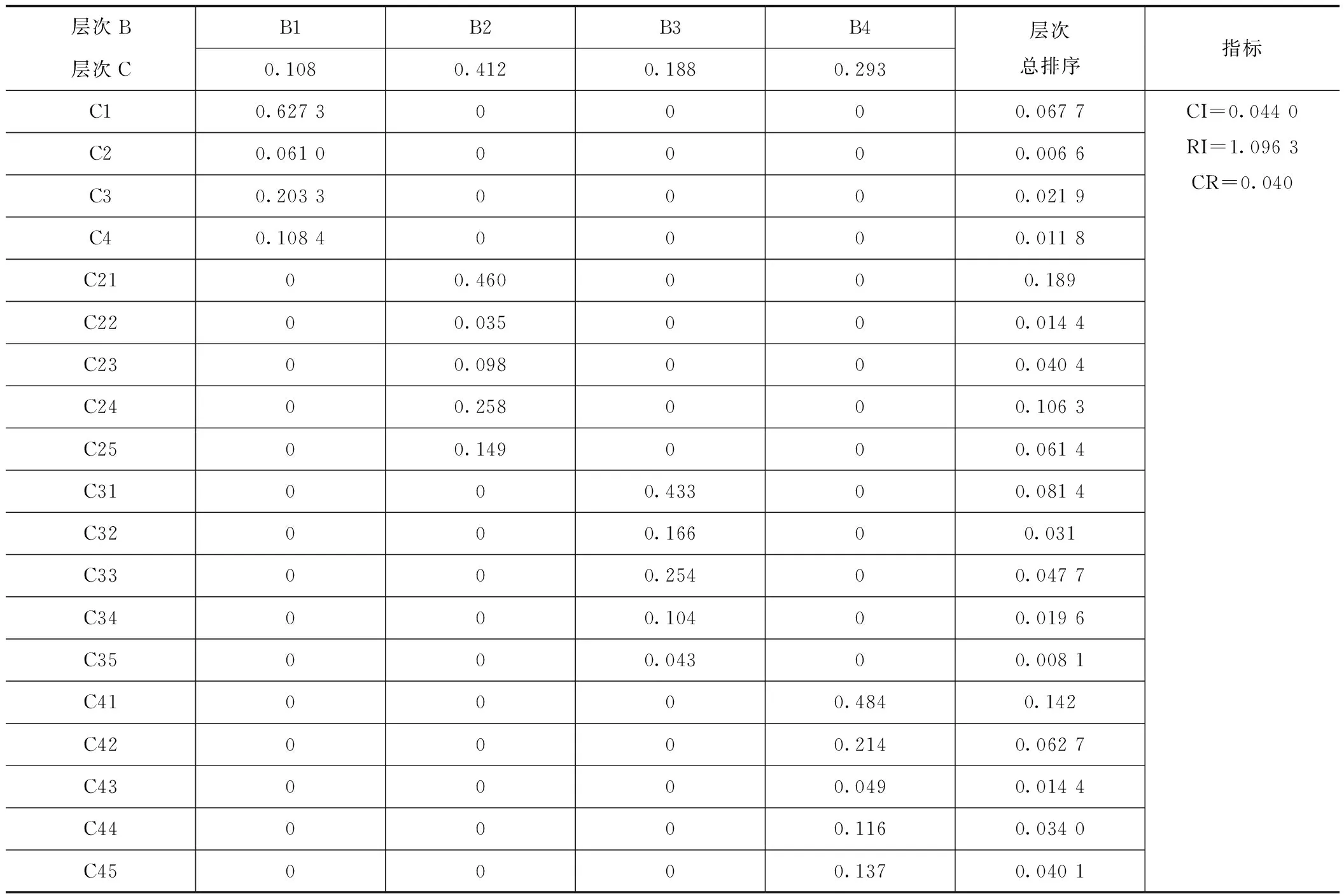
表10 层次总排序Tab.10 Total hierarchical ordering

2 结论

科学合理地规划安置小区建设与人们的幸福生活息息相关。利用层次分析方法可以清晰、直观地分析各影响因素的重要性，对各主要影响因素进行排序，根据各因素重要性程度可以有针对性地解决房屋征迁过程中出现的各种问题。但本研究具有单一性，样本量偏少，检验结果可能与实际存在偏差，仅供参考。