哈尔滨地铁粉质黏土地层隧道台阶开挖法围岩稳定性评价

全 强，郭文静，史培贺

(1.哈尔滨地铁集团有限公司，哈尔滨 150080；2.山东大学 岩土与结构工程研究中心，济南 250061)

隧道掘进中，掌子面和超前围岩的变形对隧道围岩的稳定性有着重要影响，因此保证掌子面及围岩的稳定性对施工安全来说至关重要。根据工程地质勘察报告，哈尔滨地铁工程主要为粉质黏土地层且采用台阶法开挖。依托该工程，基于超前小导管的支护机理，通过建立掌子面稳定性模型，研究其破裂机制，进行掌子面稳定性分析与评价，通过分析隧道围岩弹塑性分布，研究二次应力状态，对隧道洞身稳定性进行评估。

1 开挖掌子面稳定性评价

哈尔滨地铁隧道采用台阶法开挖，该工程的支护形式为超前注浆小导管支护、初期支护及二次衬砌相结合。但对于隧道掌子面土质较差、超前小导管参数不合理或支护措施不及时等情况，超前小导管对隧道围岩的支护作用将会大大减小，极易导致坍塌事故，所以必须根据具体工程情况进行掌子面稳定性分析。

1.1 超前小导管支护作用机理

自身加固机理：锚杆作用。将超前小导管打入隧道拱顶一定范围内，提高围岩的承载能力。浆液通道作用。小导管管体钻孔后形成通道，有利于浆液扩散，从而提高土体承载力。棚架作用。开挖初期未支护时，超前小导管对土体的支撑作用有利于掌子面的稳定。

注浆加固机理：浆液对土体的挤密压缩有利于提高围岩稳定性，注浆后土体的内摩擦角、黏聚力得以增大，抗剪能力提高。

1.2 超前小导管支护作用理论模型

综合分析超前小导管的受力状态及位移变形情况，建立如图1所示的超前小导管双参数有限长弹性地基梁受力模型。

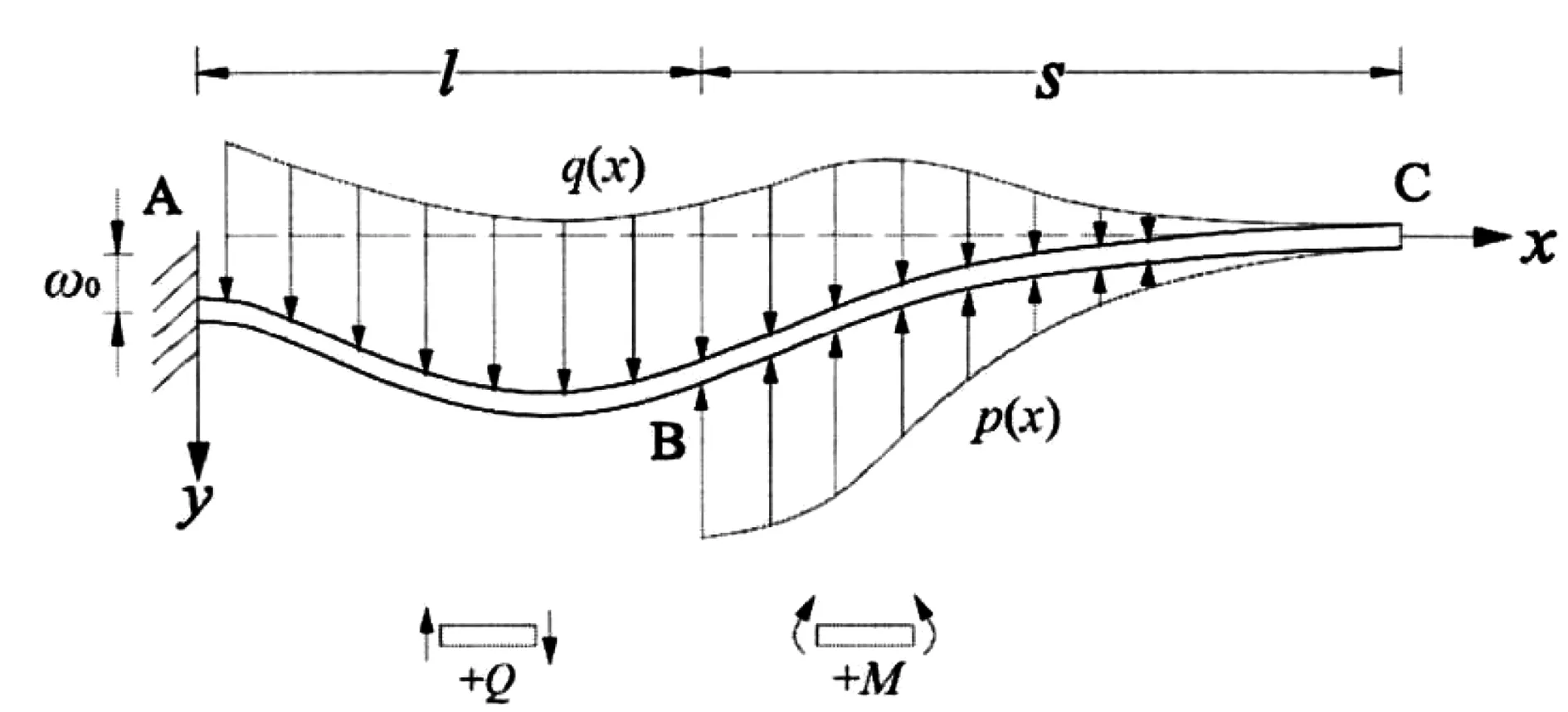
图1 导管受力模型Fig.1 Pipe stress model

对小导管进行受力分析，可得导管的弯矩剪力Q(x)、弯矩M(x)、转角θ(x)及导管内壁纵向应变ε(x)：

其中，D为导管外径，δ为导管壁厚。

1.3 超前小导管作用下掌子面稳定性定量评价

1.3.1 掌子面稳定性评价模型

基于超前小导管的支护作用，根据掌子面前方土体的破裂机制，提出一种掌子面稳定性计算模型，该模型适用于粉质黏土台阶法隧道开挖过程中掌子面的稳定性分析，如图2所示。

图2 掌子面稳定性计算模型Fig.2 Calculation model of tunnel face stability

1.3.2 掌子面稳定性定量评价

基于掌子面稳定性计算模型，对滑移体进行极限平衡分析，可得各级围岩在有无支护情况下的稳定性系数，见表1。

表1 掌子面稳定性系数Tab.1 Coefficient of tunnel face stability

参考《建筑边坡工程技术规范》(GB 50300-2013)[1]，结合表1可知，为保证掌子面稳定性，在粉质黏土地层中，对于V级围岩，无须采用超前导管支护便可保证掌子面稳定；对于Ⅵ1级围岩，须采用超前导管支护，并依据工程具体情况决定是否注浆；对于Ⅵ2级围岩，因其土质较差，超前小导管支护无法保证掌子面稳定，须采用深孔注浆加固技术或施加超前管棚支护。

2 隧道洞身稳定性评价

2.1 围岩弹塑性分布二次应力状态

假设围岩为弹塑性体，支护结构为线弹性体，忽略计算介质的自重。基于平面应变模型并采用虚拟支撑力逐步释放法[2]模拟隧道开挖过程中支护结构施作时机、围岩应力释放过程等影响，将隧道开挖过程分为初始阶段、开挖阶段、支护阶段，见图3。

图3 开挖支护不同阶段平面应变计算模型Fig.3 Plane strain calculation model of different stages of excavation and support

通过土工试验获得粉质黏土的压缩模量，换算为弹性模量[3]。基于以上计算模型对围岩弹塑性应力状态进行分析，可得：

隧道开挖前地层的初始位移场：

塑性区围岩的位移：

弹性区围岩的位移：

隧道开挖后围岩的收敛位移：

U=Ue+Up-U0

2.2 收敛约束法关键曲线

2.2.1 围岩收敛特征曲线

选取支护抗力大于最小支护力且围岩变形满足规范要求的支护时机，将所选择的不同支护时机施作初衬所得的支护压力P1代替虚拟支撑力，可得围岩收敛特征曲线，见图4。

图4 围岩特征曲线及支护特征曲线Fig.4 Surrounding rock characteristic curve and supporting characteristic curve

对松动区内滑移体进行极限平衡分析，即可得作用在支护结构上的最小支护力和最大安全塑性区范围。

2.2.2 洞身纵向变形曲线

在格栅拱架与喷射混凝土共同支护下，支护结构的刚度随时间增长不断增大，因此围岩的应力释放率必将逐渐减小并趋近于某一值。围岩以变形的方式完成应力释放过程，故应力释放率与收敛变形必存在相应的关系，采用拟合工具分析可得施加支护结构后的洞身纵向变形曲线，见图5。

图5 洞身纵向变形曲线Fig.5 Longitudinal deformation curve of the hole body

将现场拱顶沉降监测数据和理论计算值进行对比分析，计算值相比于实测值其标准误差均小于1.5，相关系数接近1。表明计算结果能够很好地反映支护施作后拱顶沉降的大小及规律。

2.2.3 支护特征曲线

基于支护结构参数，考虑钢格栅单独支护和格栅与喷混凝土联合支护[4]下的作用效果，可得到各亚级围岩的支护特征曲线，如图6～图8。

图6 V级围岩下支护特征曲线Fig.6 Support characteristic curve under V class surrounding rock

图7 Ⅵ1级围岩下支护特征曲线Fig.7 Support characteristic curve under Ⅵ1 class surrounding rock

图8 Ⅵ2级围岩下支护特征曲线Fig.8 Support characteristic curve under Ⅵ2 class surrounding rock

由图可知，对于V级围岩，支护结构所提供的最大支护反力大于支护与地层特征曲线的平衡点应力，且围岩变形满足规范要求；对于Ⅵ1、Ⅵ2级围岩，施加支护结构前，围岩已经产生较大的位移，即使支护力满足要求，也须采用超前支护，提前支护时机。

2.3 容许位移安全系数

为保证围岩变形在合理范围内，通过分析不同亚级粉质黏土的洞身收敛变化，得到洞身收敛容许位移安全系数[5]，见表2。

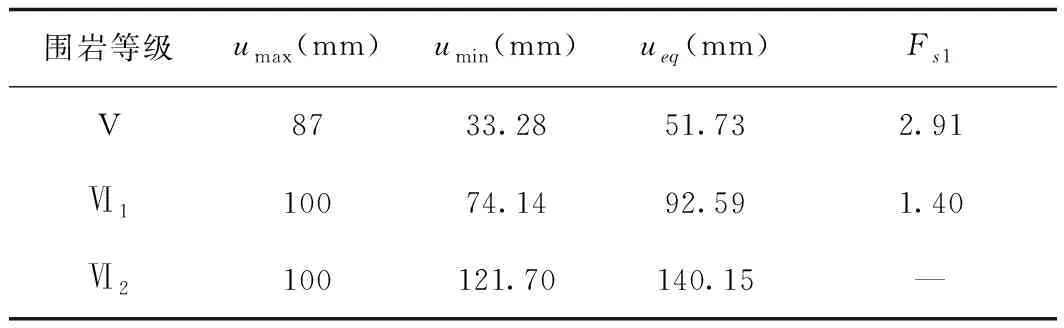
表2 洞身收敛容许位移安全系数Tab.2 Allowable displacement safety factor of hole convergence

由表2可知，在上述开挖支护措施下，V级粉质黏土的容许位移安全系数为2.91，满足施工要求；Ⅵ1级粉质黏土的容许位移安全系数为1.40，支护结构刚度也满足要求，因此建议采用超前小导管支护；对于Ⅵ2级粉质黏土，支护结构的刚度已满足要求，但在掌子面开挖前，围岩已经产生过大的收敛变形，故须在开挖前进行超前加固，以保证施工安全。

3 结论与展望

3.1 研究结论

根据超前小导管支护作用机理，对哈尔滨地铁粉质黏土隧道台阶法工程开展了围岩稳定性研究，建立了超前小导管双参数弹性地基梁的力学计算模型，提出了适用于粉质黏土地层台阶法隧道开挖的掌子面稳定性分析模型，并对掌子面进行稳定性评估。结果表明：对于V级围岩，无须采用超前导管支护便可保证掌子面稳定；对于Ⅵ1级围岩，须采用超前导管支护，并依据工程具体情况决定是否注浆；对于Ⅵ2级围岩，因其土质较差，超前小导管支护无法保证掌子面稳定，须采用深孔注浆加固技术或施加超前管棚支护。分析了围岩的弹塑性分布二次应力状态，并根据收敛约束法得到围岩收敛特征曲线、洞身纵向变形曲线和支护特征曲线，基于容许位移安全系数，对隧道洞身的稳定性进行了评估。结果表明，支护结构的承载力满足施工安全要求，但Ⅵ1、Ⅵ2级粉质黏土隧道应借助超前支护，以保证围岩稳定性。

3.2 展望

以下方面有待进一步开展：通过土压力计算经验公式开展掌子面稳定性分析，下一步应根据试验及计算得到精确土压力值。通过理论模型和数值计算，分析了隧道掌子面前方土体的破裂模式，今后应结合模型试验来验证土体的破裂形态。主要考虑超前小导管的纵向“棚架”作用，暂未分析其横向成拱作用，今后应在该方面展开研究，以完善超前小导管的支护理论。