基于Java语言的杨辉三角程序设计与探讨
2022-04-02夏清欢,应沈静,陶骏,龚勇,宋卫卫
夏清欢,应沈静,陶骏,龚勇,宋卫卫



摘要:文章首先介绍了杨辉三角和二项式的基本原理,提出了三种求杨辉三角的程序算法,这三种算法分别是:组合数法、递归法和队列法,使用Java语言在Eclipse平台上实现了这三种算法,并对这三种算法的运行效率和时间复杂度进行了测试分析,得出了队列法最优的结论。
关键词:杨辉三角;二项式;递归;队列
中图分类号:TP391 文献标识码:A
文章编号:1009-3044(2022)33-0034-04
1 引言
杨辉三角本质上是一组数的集合,是二项式系数呈三角形一种几何排列,其通过图形直观地显示了二项式系数,把组合数内在的一些代数性质直观地从图形中体现出来,是把一系列离散型的正整数与图形相结合后所形成的一个特殊的三角形。杨辉三角是由我国南宋数学家杨辉发现的,是中国古代数学一项优秀的研究成果,法国科学家帕斯卡在390多年后也发现了此成果,所以杨辉三角有时候也称为帕斯卡三角。
Java是一种面向对象高级编程语言,不仅具有面向对象语言的继承、封装和多态优点,还扬弃了难以理解的一些理论,比如多继承,所以Java语言具有功能强劲和简单实用两个特点,允许程序员快速高效地进行复杂编程。Java语言还具有分布式、平台独立与可移植性、多线程和动态性等特点。Java语言可以实现桌面应用程序、Web应用程序、分布式系统和嵌入式系统应用程序等[1]。
本文运用Java语言中的桌面应用程序实现了杨辉三角的形成和显示,而且使用组合数、递归和队列三种不同的方法进行了实现,并对这三种方法的优劣进行了对比和分析。
2 杨辉三角
一个二项式如下表示:
[(x+y)n=C0n*xn+C1n*xn-1*y+C2n*xn-2*y2]+...+[Cnn*yn] (1)
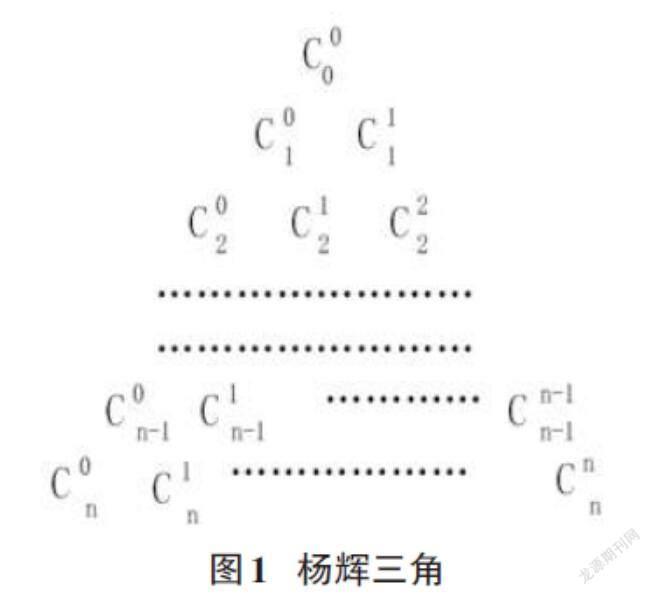
杨辉三角是由一系列二项式中的系数(组合数)构成的,一个杨辉三角的显示图如图1所示。
<E:\2022知网文件\33\2xs202233\Image\image2.png>
图1 杨辉三角
第一行为k=0的二项式的系数,第二行是k=1的二项式的系数,以此类推,第n+1行是k=n的二项式的系数,杨辉三角所对应的图形是一个等腰三角形,两条腰上的数值都是1,其余的一般项的数值满足:
[Crk=Crk-1]+[Cr-1k-1] (2)
一般项的数值等于上一行相邻的两个项的数值之和[2]。
3 程序设计
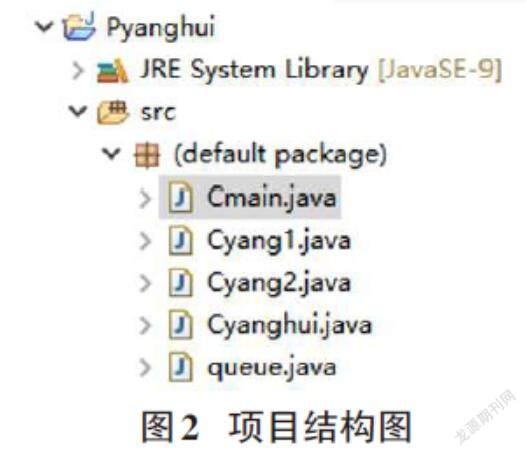
由于杨辉三角中数值具有规律性,所以可以通过计算机编程实现,本研究采用了三种不同的方法实现了杨辉三角,所采用的编程语言是Java语言,具体Java版本号为JDK1.9,开发平台使用是Eclipse 4.11,项目结构如图2所示。
<E:\2022知网文件\33\2xs202233\Image\image3_1.png>
图2 项目结构图
项目名称为Pyanghui,然后在此项目中建立了5个类,Cmain是主函数入口类,Cyang1是通过求组合数实现杨辉三角的类,Cyang2是通过递歸实现杨辉三角的类,Cyanghui是通过队列实现杨辉三角的类,queue为队列类[3]。
3.1 组合数法
组合数法的思想是:先求排列值[Pnn]=n!,再求组合值[Cmn]=n!/(m!*(n-m)!),然后再分行显示,每行先打印相应的空格数,再显示一系列组合的值,其对应的流程图如图3所示。
<E:\2022知网文件\33\2xs202233\Image\image4_1.png>
图3 方法1流程图
具体的java程序代码如下:
publicclass Cyang1 {
//求阶乘n!函数
publicint mul(int n)
{
int m;
if(n==0)
m=1;
else
{m=1;
for(int i=1;i<=n;i++)
m=m*i; }
return(m);}
//求组合数[Cmn]函数
publicint zuhe(int n,int m)
{if(n<m) //不合法情况
{System.out.println("不合法!!!");
System.exit(0);
return(0);}
else
{return(mul(n)/(mul(m)*mul(n-m))) ;}
}
//打印组合数[Cmn]函数
publicvoid ydisplay(int n,int m)
{System.out.println(zuhe(n,m));}
//求n行杨辉三角函数
publicvoid calyang(int n)
{//j控制行数
for(int j=0;j<=n;j++)
{//打印相关空格
for(int m=0;m<=n-j;m++)
System.out.print("");
//显示一行中的所有组合数
for(int k=0;k<=j;k++)
{
System.out.print(zuhe(j,k));//换行
System.out.print("");//两个数之间打印空格
}
System.out.println();//换行
}}
}
显然ydisplay函数是通过二重循环实现,而且最里层循环调用了zuhe函数,zuhe函数又调用了mul函数,mul函数使用一重循环实现,其问题规模为n,所以mul函数和zuhe函数的算法时间复杂度为O(n),ydisplay函数的时间复杂度为O([n3])。
Java语言里int值占用4个字节,其取值范围为(-2147483648到2147483647),13!>2147483647,所以当用mul函数求13的阶乘时会溢出,calyang函数只能求0到12的杨辉三角[4]。
<E:\2022知网文件\33\2xs202233\Image\image5.png>
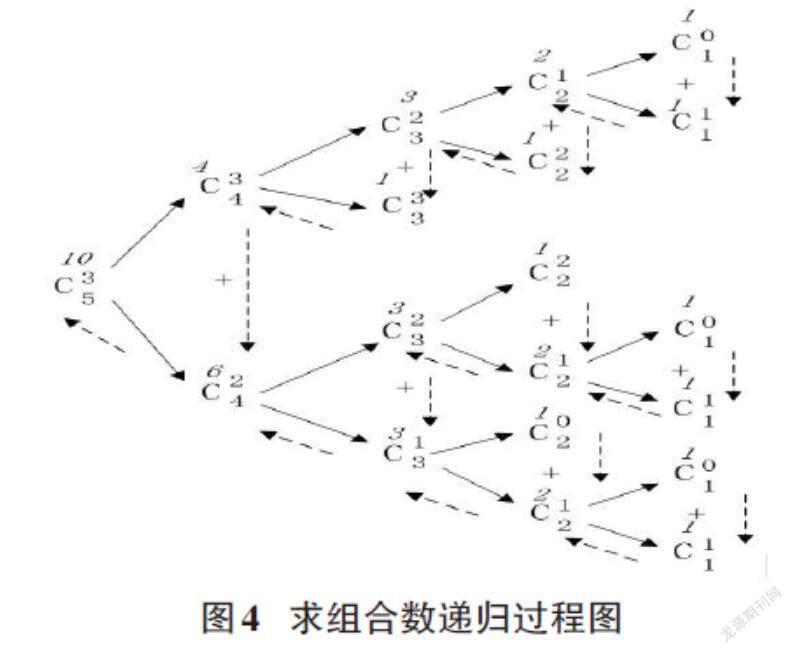
图4 求组合数递归过程图
3.2 递归法
杨辉三角中的组合数[Cmn]有一定规律,其规律为:如果m=0或者m等于n,则此组合数为1,否则[Cmn]=[Cmn-1]+[Cm-1n-1],例如求[C35]的过程如图4所示。
此方法对应算法思想和流程图除了求组合数有差异外,其余的均类似,具体的Java代码为:
public class Cyang2 {
//求组合数函数,n为上标,m为下标
public int caly(int n,int m)
{
//判断合法情况,上下标都是非零整数,上标大于等于下标
if(n>=0&&m>=0&&n>=m)
{ if(m==0)
//递归基1:第一列为1
return(1);
else
if(n==m)
//递归基2:行等于列时返回1
return(1);
Else
//遞归调用
return(caly(n-1,m)+caly(n-1,m-1));}
Else
//不合法时返回-1
return(-1);}
//显示杨辉三角函数,n为杨辉三角行数
public void ydisplay2(int n)
{//i控制杨辉三角行数
for(int i=0;i<=n;i++)
{//显示每行的空格
for(int m=0;m<=n-i;m++)
System.out.print("");
//打印每行的组合数,j控制每行的具体数目
for(int j=0;j<=i;j++)
System.out.print(caly(i,j)+"");
//换行
System.out.println();
}}}
此方法也是通过二重循环实现,其中内层循环调用递归函数caly,递归函数的时间复杂度为O(n),所以此方法的时间复杂度也为O([n3])。通过此方法求组合数不涉及乘法,只使用了加法,当n=30时才会发生溢出,所以此方法能求从n=0到n=29的杨辉三角。递归法也有其相应的缺陷,很多组合数被重复运算多次,降低了算法的效率,例如在图4中,[C12]被计算了3次[5]。
3.3 队列法
队列法的基本思想为:(1)当杨辉三角只有一行时,打印相应空格和1;(2)当杨辉三角有n行时,先执行(1),然后0进队列,0是第一行和第两行杨辉三角组合数的分隔值,然后连续两个1进队列,此时队列有队尾到队首的元素,分别为1、1、0,一个0再进队列,这个0是第二行和第三行杨辉三角组合数的分隔值,此时队首值poll值出,因为如果当前杨辉三角组合值不在边界,其等于上一行相邻元素之和,要显示的值evs等于出队值poll加当前队首值first,如果evs>0,则显示相关空格和evs,如果firstl等于0,不再对队列进行操作,换行显示下一行的杨辉三角值;(3)反复进行第二步,直到第n行的杨辉三角值显示完毕。具体的求三行杨辉三角的例子如图5所示。
<E:\2022知网文件\33\2xs202233\Image\image6.png>
图5 求组合数递归过程图
左边三个虚线方框代表求三行杨辉三角组合值的过程,右部三个三角形图形表示显示杨辉三角组合值的过程。初始队列为空,显示1,对应第一行的杨辉三角值;0、1、1、0按顺序进队列,0出队列,0不显示,0加1等于1进队列,1出队列,显示空格和1,1加1等于2进队列,1出队列,1加0等于1进队列,0不再出队列,此时第二行显示完毕,进行换行;0进队列,此时队列为0、1、2、1、0,0出队列不显示,0加1等于1进队列,然后1出队列,显示空格和1,1加2等于3进队列,2出队列,2加1等于3进队列,1出队列,0加1等于1进队列,显示1和空格,0不再出队列,此时第三行显示完毕,进行换行,队列中的值为1,3,3,1,0,这是为第四行显示做准备的,显然在显示第n行杨辉三角值的过程中,第n+1行的杨辉三角值已经求好存储在队列中[6]。
具体的Java代码为:
public class Cyanghui {
//杨辉三角从0到n总共n+1行
public void fyang(int n)
//处理第一行情况
{if (n==0)
{for(int i=1;i<=n;i++)
System.out.print("");
System.out.println('1');}
else
//其余情況
{for(int i=1;i<=n;i++)
System.out.print("");
System.out.println('1');
//创建队列
queue Q=new queue();
Q.offer(0);
Q.offer(1);
Q.offer(1);
int xfir=0;
int evs=0;
for(int k=1;k<n;k++)
//处理空格
{for(int i=1;i<=n-k;i++)
System.out.print("");
//换行标志0进队列
Q.offer(0);
do
{
xfir=Q.poll();
//大于0才显示
if(xfir>0)
System.out.print(xfir+"");
evs=xfir+Q.first();
Q.offer(evs);
xfir=Q.first();
} while(xfir>0);//只有队首值大于0才继续执行
System.out.println();
}}}}
队列类 queue可以通过自己编写实现,也可以使用Java语言中队列类进行实现。
此方法是通过三重循环实现,所以此方法的时间复杂度也为O([n3])。通过此方法求组合数不涉及乘法,同样只使用了加法,当n=30时才会发生溢出,所以此方法能求从n=0到n=29的杨辉三角。此方法没有重复计算组合数,所以算法的效率高于方法二。
3.4 算法实验分析
在Cmain类中使用如下代码对这三种算法进行运行时间计算:
long Tbegin=System.nanoTime(); //获取算法开始时间,单位为纳秒
分别运行三种方法;
long Tend=System.nanoTime(); //获取算法结束时间
System.out.println("算法运行时间: "+(endTime-startTime)+"ns");
在CPU为酷睿5(CORE5)和操作系统为Win10的工作站上分别运行三种算法,三种算法的运行时间和对应行数的关系如表1所示。
表1 算法运行时间和行数对照图
[算法
时间(纳秒)
行数 5行 10行 15行 20行 25行 组合数 2465400 3962150 不支持 不支持 不支持 递归 2520000 3989950 8245200 12647200 17567900 队列 2149900 3679900 7388300 10290100 14602600 ]
通过表1可以得出队列法最优,递归法的算法效率次之,而组合数法因为溢出的缘故,其只能支持0到12行的杨辉三角的计算[7]。
4 结论
本研究阐述了二项式的基本原理,二项式的值是杨辉三角的基本组成元素,使用Java语言和Eclipse平台通过组合数、递归和队列三种算法实现了杨辉三角的运算和显示,并对这三种算法的时间复杂度和效率进行了分析,得出了递归算法最优,其运行时间和算法效率都高于其余两种算法。
本文所介绍的三种算法的运行范围因为整数溢出的缘故有限,组合数算法只能求行数从0到12的杨辉三角,递归法和队列法只能求行数从0到29的杨辉三角,运行范围可以考虑通过字符队列和大数加法进行扩大,这也是下一步的研究方向[8]。
参考文献:
[1] 王先东.杨辉三角中的奇数与偶数[J].数学通报,2009,48(5):62-63,66.
[2] 杨明顺.杨辉三角的若干性质研究[J].渭南师范学院学报,2016,31(4):9-12.
[3] 李旭东.再探“杨辉三角”中的行列式[J].数学学习与研究,2013(23):111.
[4] 冯洁,吴芳.探讨C语言中输出杨辉三角的教学方法[J].电脑知识与技术(学术交流),2007,3(13):113-113,115.
[5] 宋钰.经典数据结构队列的研究和实现[J].电脑编程技巧与维护,2019(12):14-15.
[6] 陈竹云,叶雯.数据结构中队列的应用研究[J].电脑知识与技术,2017,13(3):5-7.
[7] 沈华.数据结构课程中栈和队列实验教学方案设计[J].教育教学论坛,2016(24):274-276.
[8] 耿国华.数据结构[M].北京:高等教育出版社,2005.
【通联编辑:代影】
