基于Landsat 8遥感影像的地上生物量模型反演研究
2022-04-02赵天忠吴发云
周 蓉,赵天忠*,吴发云
(1.北京林业大学,国家林业草原林业智能信息处理工程技术研究中心,北京 100083;2.国家林业和草原局调查规划设计院,北京 100714)
森林生态系统是陆地生态系统重要组成部分,全球森林面积约占全球陆地面积的31%,约为40.6亿hm2[1]。森林生物量能够直接反映森林固碳能力,体现森林经营水平,为研究生态及林业问题提供基础数据,在森林生态系统和全球气变化研究发挥着不可替代的作用[2-5]。传统森林生物量获取主要依托人工实地调查森林清查数据或小范围样地抽查数据[6],但耗时长、效率低、易造成森林植被破坏、难在大区域内广泛应用。随着遥感技术在林业工作的广泛应用[7],其为估算森林生物量提供了新思路[8]。
遥感数据中蕴含着丰富的光谱信息,不仅记录了森林水平结构的植被信息,也能够准确地反映植被类型、生长状况,具有覆盖范围广、动态更新时间短的优势。杨伟志等[9]、何矣等[10]、刘芳等[11]等探讨了不同遥感数据与地上生物量之间的关系,采用线性回归方法分别建立西宁市南北山区域生物量回归估测模型、汝城县森林生物量预测模型、北京市针叶林和阔叶林地上生物量模型。虽然回归模型在一定程度上能够实现地上生物量的估算,且具有简单易懂的优点,但要求样本数据具有正态性、独立性,而实际数据往往难以满足假设条件,同时线性回归法也不能全面地解释各数据之间的关系,因此将非参数的估测方法引入森林参数反演中[12-13]。李丹丹等[14]基于旺业甸林场的Landsat TM影像和DEM数据,提取影像中的灰度值和植被因子信息作为输入因子,采用BP神经网络构建了该地区的针叶林生物量模型;李明泽[15]基于Landsat数据,采用多种方法建立了东北林区各区域的森林生物量估算模型,与BP神经网络、Erf-BP神经网络、偏最小二乘算法相比,逐步回归模型估测精度较低;刘笑笑[16]采用RF-RFE算法、逐步回归算法、支持向量机算法分别对大兴安岭地区资源三号遥感影像中提取的49种特征变量进行筛选,实验表明基于随机森林的向后迭代算法(RF-RFE)具有更强的通用性,许振宇等[17]分别以不同遥感影像为数据源,对比了传统多元回归算法与机器学习算法在变量筛选、生物量模型构建过程中的作用;邱布布等[18]应用随机森林算法,对比了Landsat 8 OLI影像、Landsat 7 ETM+影像对杭州市绿地地上生物量估算模型的影响。
大量研究表明机器学习算法建立的生物量预测模型具有更强的拟合性、更好的预测精度和更广泛的通用性。但这些研究大都对比传统回归法与机器学习方法,或对比了不同的机器学习算法之间的差异,忽略了同一种机器学习算法间不同训练函数对模型精度的影响。综上所述,本研究以吉林省延边朝鲜族自治州汪清县的主要针叶纯林树种为研究对象,在对比不同机器学习算法之间优劣性的基础上,分析同一种机器学习算法中不同训练函数带来的影响,以此探讨不同机器学习算法及同一种算法间不同训练函数在反演地上生物量模型中的适用性。
1 研究区概况与研究数据
1.1 研究区概况
以吉林省延边朝鲜族自治州汪清县为研究区,该区域位于吉林黑龙江2省交界处,延边朝鲜族自治州东北部,地形地貌以山地为主,地势高低起伏,属长白山系老爷岭山脉;具体地理位置为43°06′-44°03′N,128°54′-130°41′E,东邻俄罗斯,南沿朝鲜,县内辖区面积9 016 km2;平均海拔为806 m;年平均气温为4.9 ℃,全年总降水量约为580 mm,全年总日照时间约2 234 h,属中温带湿润温凉气候区。境内森林资源丰富,林业总面积为32.9万hm2,有林地面积26.8万hm2,森林覆盖率达到81.4%,主要分布的树种为云杉(Piceaasperata)、红松(Pinuskoraiensis)、冷杉(Abiesfabri)、落叶松(Larixgmelini)等[19]。
1.2 地面调查数据获取及预处理
根据研究区的自然资源分布状况,选择区域内典型树种——冷杉、云杉、落叶松为研究对象,在研究区内共设置了128个半径为15 m、面积为0.07 hm2的圆形样地。调查样地的选择主要依据林分的树种组成、样地的郁闭度及平均树高范围。在样地调查过程中,首先,记录了样地的地貌、坡度、坡向、林分起源等基础信息;其次,在样地范围内每木检尺,起测胸径为5 cm,采用胸径尺获取每株单木1.3 m处的胸径,采用VL5激光超声波测高测距仪获得了每木树高、枝下高信息;最后,通过差分GPS解算获得样地样木地理坐标。
在本研究中,样地尺度地上生物量信息根据汇总单木尺度信息获得,以实测的单木树高、胸径因子数据为基础,采用我国林业行业标准文件[20-22]提供的地上生物量公式得到单木地上生物量,具体计算如式(1)-式(3)所示,并将其汇总到样地尺度。
冷杉:M=0.069 45×D2.057 53×H0.508 39(1)
云杉:M=0.080 7×D2.259 57×H0.256 63(2)
落叶松:M=0.068 48×D2.015 49×H0.591 46(3)
式中:M为生物量,D为胸径,H为树高。

表1 样地样本调查因子统计
1.3 Landsat 8 OLI数据获取及预处理
使用2018年6月3日采集的Landsat 8 OLI影像作为光学遥感数据,数据航带号为115/30。Landsat 8陆地资源卫星于2013年2月11日发射,在保持Landsat 7卫星特征的基础上,对波段数量、光谱范围、影像的分辨率等都进行了改进。Landsat 8 OLI共分为9个波段,空间分辨率为30 m,其中包括1个分辨率为15 m的全色波段,数据投影方式为WGS84。Landsat 8 OLI影像数据的各波段信息如表2所示。
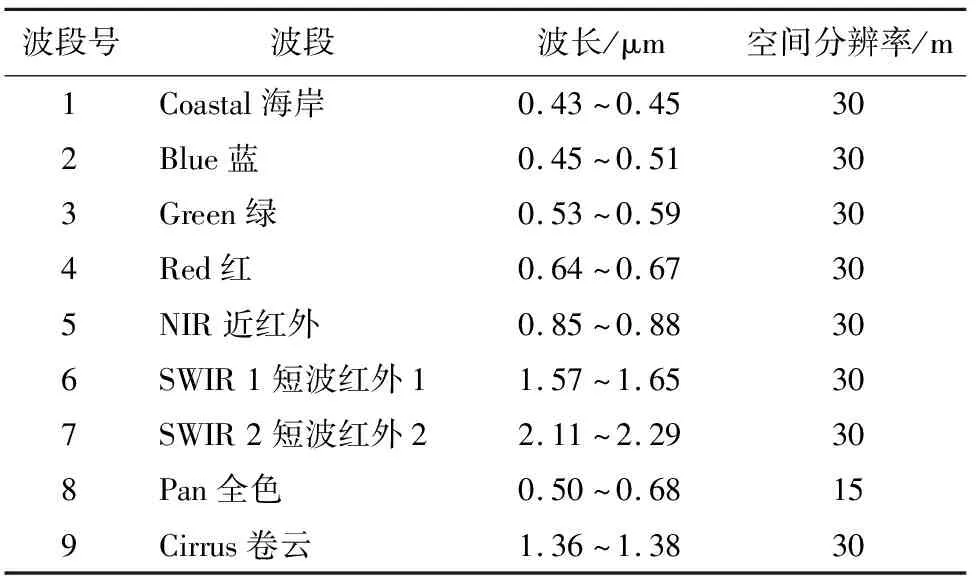
表2 Landsat 8 OLI影像波段信息
遥感影像的质量易受到大气条件等自然因素和传感器成像等硬件设备的影响,为了增强遥感影像的信息量,保证光谱特征的准确性,本文对研究区的Landsat 8 OLI影像进行辐射定标、大气校正等预处理,并从预处理后的遥感影像上提取了森林结构的光谱特征信息、植被指数信息。
1.3.1 辐射定标 辐射定标的原理是将传感器中所记录的数字量化值或电压转化为绝对辐射亮度值,其目的是消除传感器在成像过程中带来的误差[23-24]。采用ENVI软件对图像进行辐射定标处理,通过定标工具(Radiometric Calibration)读取元数据文件,并将其进行自动定标。
1.3.2 大气校正 在辐射定标的基础上,对影像进行大气校正处理,其目的是消除大气和光照等外部因素带来的影响[25]。使用ENVI软件中FLAASH大气校正工具对影响进行大气校正。
1.3.3 变量提取 本研究基于预处理的研究区影像共提取34个遥感特征因子,根据计算方式及特征因子的含义可分为3组。原始波段变量:为完整的反映了影像的原始特性,选取第2波段~第7波段参与研究。波段组合变量:为丰富影像信息,凸显不同影像特征,提取B24、B53、B65、B74、B76、B345、B547、VIS234、Albedo、B4/Albedo10个波段组合变量。植被指数变量:其本质是地物光谱反射率的差异比值,本研究获取了大气阻抗植被指数ARVI、差值植被指数DVI、增强型植被指数EVI、修正型土壤调整植被指数MSAVI、修正型简单比值植被指数MSR、归一化植被指数ND43、ND67、ND563、NDVI、非线性指数NLI、垂直植被指数PVI、重归一化植被指数RDVI、简单比值植被指数RVI、土壤调整比值植被指数SARVI、土壤调整植被指数SAVI、有效叶面积指数SLAVI、转换型植被指数TNDVI、中红外植被指数VI3共18个植被指数变量[26]。
2 研究方法
2.1 随机森林
随机森林(random forest,RF)[27]是一种以决策树为基础的bagging并行集成学习算法,其随机性主要体现在样本的随机选择和特征变量的随机选择上。本研究采用随机森林算法实现特征重要性排序,主要是通过从sklearn库中调用feature_importances_方法实现,其目的是判断输入特征在预测变量过程中的有用程度,通过比较各因子的相对得分,从而判断哪些特征与目标最相关,实现数据的深层理解,有效地减少输入特征的数量,提高预测模型的精确性和有效性。
2.2 BP神经网络
BP(back propagation)神经网络是误差逆向传播的多层前馈神经网络,由输入层、隐含层、输出层构成,其中心思想是利用隐层神经元判断当前输出层的误差大小,并参照误差大小调整连接权值和阈值,直到误差满足停止条件则重复上述迭代过程[28]。BP神经网络的拓扑模型如图1所示。
2.3 SVM支持向量机
支持向量机(support vector machine,SVM)于1995年由Cortes and Vapnik提出[29],是一种适用于小样本模型训练的二类分类器,该算法的目的是得到一个超平面,使得2类可分数据进行准确分类。不同的SVM核函数之间存在一定的性能差异,核函数将空间内线性不可分的数据映射到高维的特征空间,从而使数据在特征空间内实现可分,一般常使用线性核函数、RBF核函数、多项式核函数3种核函数来完成输入空间到特征空间的多维映射,式(4)~式(6)给出了3种核函数的表现形式。
k(xi,xj)=xiT×xj
(4)
(5)
k(xi,xj)=(xiT×xj)d
(6)
式中:σ>0为高斯核的带宽;d≥1为多项式的次数。
2.4 模型评价指标
为了更加全面、有效地对模型进行评价,引入多种评价指标,对模型精度进行分析和判断。
决定系数(R-Square,R2)
(7)
均方根误差(root mean square error,RMSE)
(8)
平均绝对误差(mean absolute error,MAE)
(9)

3 结果与分析
3.1 基于随机森林筛选变量
地上生物量与遥感影像有着复杂却密切的关系,如何从大量的遥感影像变量中筛选出与地上生物量紧密相关的变量用于后续的模型研究是极为重要的。因此本研究在进行数据归一化的前提下,通过采用随机森林的方法分析各个变量在模型构建中的特征重要性,选取特征重要性较高的特征变量参与模型的构建。34个遥感因子与地上生物量的特征重要性如图2所示,通过观察特征重要性的大小,并考虑了特征变量的独立性确定最后应用于建模的10个特征变量,筛选结果如图3所示。
从图2可以看出,原始波段变量中B3绿波段、B4红波段、B6短波红外1、B7短波红外2,波段组合变量中B345、Albedo变量、VIS234变量,植被指数变量中PVI、ND67、ND563与所需估测的地上生物量之间的相关关系较高且显著,这说明因变量与自变量之间有较好的线性关系,因此将这10个因子作为建模变量,参与后续试验。
3.2 BP神经网络模型建立与分析
3.2.1 网络结构的确定 输入层节点数为10,输出层节点数为1,根据式(10)确认隐含层为4~13,通过对比试验,确认确认BP神经网络模型结构为10∶12∶1。
(10)
式中:l为隐含层节点数;n为输入层节点数;o为输出层节点数;m为1~10的任意整数。
3.2.2 传递函数及参数确定 设置tansig函数作为隐含层的传递函数;以线性传递函数purelin作为输出层的传递函数。设置学习速率为0.01,最大迭代次数为1 000,目标精度为0.001,最大验证失败次数为10次。
采用25%的样本数据对模型精度进行验证,采用BP神经网络算法构建的地上生物量模型预测的样地地上生物量值与实测地上生物量值的对比结果如图4所示,图中直线为1∶1辅助判断线。
3.3 SVM支持向量机模型建立与分析
为了探究不同SVM支持向量机的核函数的使用对地上生物量模型预测精度带来的影响,本研究采用SVM的3种核函数分别构建了地上生物量反演模型,其预测地上生物量值与实测值的对比结果如图5所示,图5中直线为1∶1辅助判断线。
3.4 地上生物量估算模型对比分析
表3汇总了2种算法构建的5个地上生物量模型的精度评价情况,具体模型构建结果如下。利用BP神经网络算法估算生物量模型时,贝叶斯正则化算法模型的决定系数R2为0.672 1、RMSE为4.263 7、MAE为3.211 8,其估算精度高于L-M算法模型(R2为0.602 9、RMSE为5.096 9、MAE为4.166 9);利用SVM支持向量机算法构建生物量模型时,多项式核函数模型预测精度(R2为0.487 7、RMSE为5.763 7、MAE为4.176)低于线性核函数模型(R2为0.585 8、RMSE为5.859 4、MAE为4.24)和RBF核函数模型(R2为0.561 9、RMSE为5.600 9、MAE为3.89)。
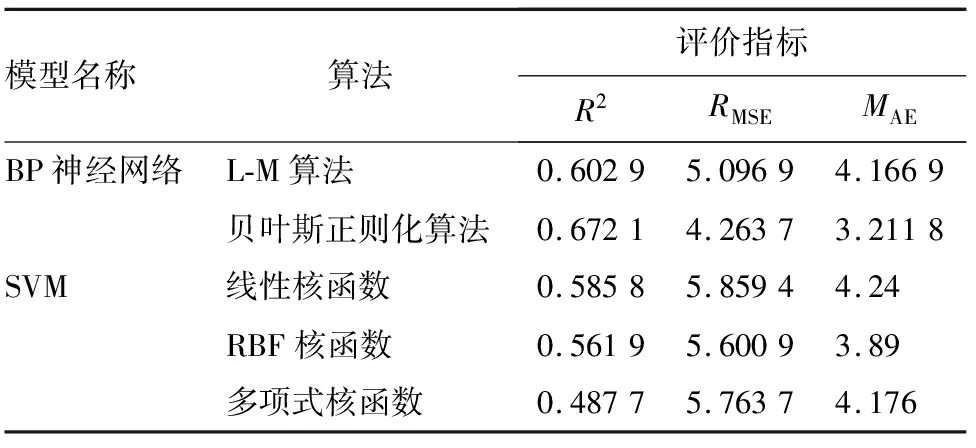
表3 地上生物量模型精度评价
对比BP神经网络算法、SVM支持向量机算法分别构建的地上生物量模型,可知BP神经网络算法模型的整体预测精度要高于SVM算法,具体来说,L-M算法、贝叶斯正则化算法构建的模型决定系数R2均大于0.6,而SVM算法中平均决定系数R2约为0.54,且RMSE、MAE也均大于BP神经网络模型。
综上,采用贝叶斯正则化算法构建的BP神经网络地上生物量模型的预测效果最佳,该模型各层网络的表达式如表4所示。
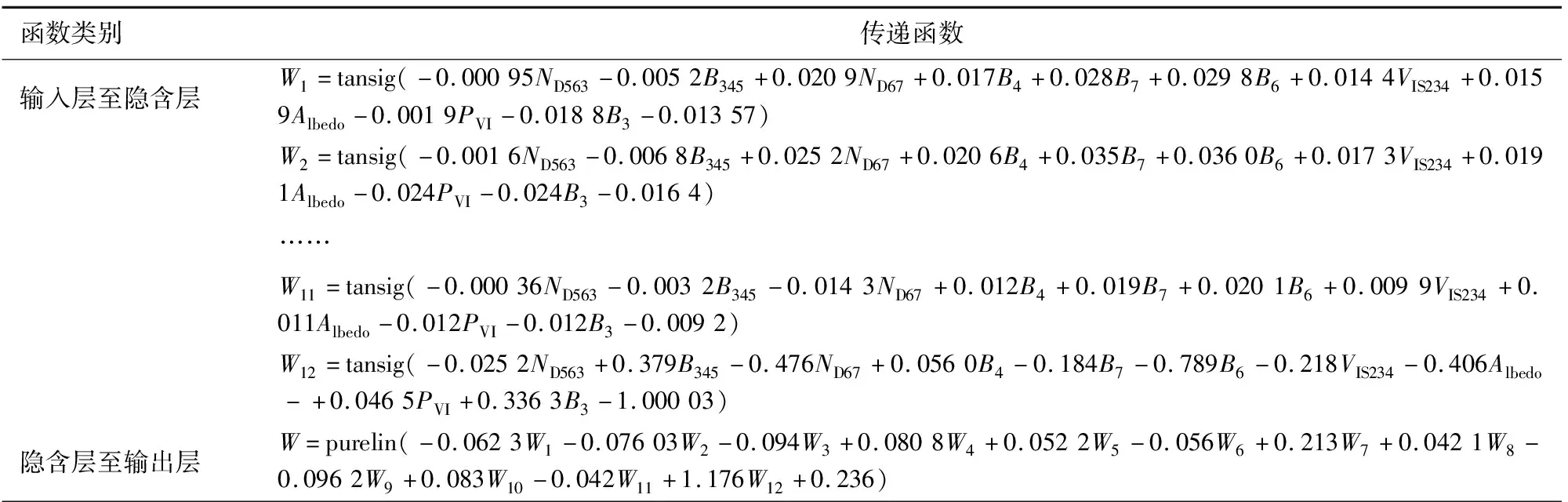
表4 BP神经网络各层传递函数表达式
4 结论与讨论
以吉林省延边朝鲜族自治州汪清县的地面调查数据、Landsat 8 OLI遥感影像数据为基础,探究了遥感影像特征因子与地上生物量之间的关系,在采用随机森林算法筛选因子变量的基础上,构建了以BP神经网络、SVM支持向量机为基础算法的多种地上生物量估测模型。
综合对比各模型的拟合结果可知,以贝叶斯正则化算法为BP神经网络训练算法的地上生物量模型的表现优于其他函数结构。从模型拟合的决定系数R2来看,该模型的决定系数最大,且RMSE和MAE较小。
基于BP神经网络建立的预测模型对地上生物量有更好的解释。对比BP神经网络算法构建的2种模型、SVM支持向量机算法构建的3种模型,可知BP神经网络算法各训练函数所构建的模型,其拟合精度都优于SVM支持向量机的模型。
SVM支持向量机模型中,多项式核函数对数据的解释能力最差。对比线性核函数、RBF核函数、多项式核函数构建的3种生物量模型,以线性核函数、RBF核函数作为算法构建的模型其决定系数R2无显著差异,但二者均大于多项式核函数构建的地上生物量模型。
本研究所构建的各模型均能较好地估测地上生物量,且也能较好地体现各机器学习算法之间不同训练函数的差异性,但也存在一定的不足之处。如何将Landsat 8 OLI遥感影像数据与地面实测数据相结合,提高模型的估测精度,并实现其他森林结构参数的估测,是今后研究的重点内容。
