裂纹扩展增量对裂纹扩展稳定性影响的研究

朱凯林，米彩盈

西南交通大学 机械工程学院，四川 成都 610031

0 前言

工程上构件疲劳失效的主要原因是构件危险部位裂纹的萌生及扩展，目前机械结构疲劳裂纹剩余扩展寿命计算都是基于Paris公式，计算出裂纹尖端的应力分布情况和应力强度因子（stress intensity factor，SIF）大小，结合相应工程判据计算出裂纹尖端扭转角度和材料断裂韧性来确定裂纹扩展速率及其扩展寿命［1］。

利用裂纹尖端应力计算SIF需要裂纹尖端具有非常细密的网格，而常用的有限元分析软件如ANSYS、Abaqus和Nastran等难以对局部网格进行理想的细化。FRANC3D是FAC公司开发的新一代裂纹分析软件，不仅可以对局部裂纹尖端进行网格细化，还可以在裂纹尖端生成三圈环状奇异单元，提高计算精度，并且提供了ANSYS、Abaqus和Nastran等软件接口［2］。

目前有关动态裂纹的研究最经典的案例是利用拉格朗日有限差分法分析阶跃载荷作用下中心裂纹板的动态应力强度因子。彭英［3］应用相互作用积分法计算动态应力强度因子，考虑了裂纹面接触作用、冲击载荷形式、裂纹长度、裂纹角度及裂纹位置等参数的影响；姜伟［4］采用将动态有限元分析过程和相互作用积分相结合的方法，在有限元分析软件ANSYS中求解动态应力强度因子。尽管动态求解方法更趋近于实际，但其计算过程极其复杂，不适用于复杂模型，故常用的疲劳裂纹扩展分析方法是通过设置不同的静态裂纹分析步进行迭代，在相邻两分析步中，很重要的一个参数是裂纹扩展增量。扩展增量越大，裂纹扩展分析步较少，计算时间短；增量越小，裂纹扩展分析步较多，计算精度高，但计算时间较长。故裂纹扩展增量的确定对裂纹扩展仿真分析有重要意义。而在实际的裂纹扩展仿真分析中，诸多研究学者往往根据结果精度的需求来确定裂纹扩展增量的大小，忽略了扩展增量对裂纹扩展稳定性的影响，为探究这一问题，本文结合FRANC3D软件，分析了在不同扩展增量下紧凑拉伸（CT）试样的裂纹扩展稳定性情况，并根据贯穿裂纹SIF的分布特点分析了裂纹凸凹扩展的原因及裂纹扩展增量的确定方法，为裂纹扩展剩余寿命计算问题提供参考依据。

1 疲劳裂纹扩展分析方法

对结构进行疲劳裂纹扩展分析首先是建立模型，本文采用HyperMesh对模型进行网格划分并将其导入Abaqus定义材料属性、载荷以及约束，并提交分析。然后导入FRANC3D中在裂纹扩展区域引入裂纹并重新划分网格，得到新的完整有限元模型后再提交到Abaqus中进行应力分析，计算出裂纹尖端的SIF值，根据SIF大小计算出裂纹尖端节点的局部扭转角度，结合给定的裂纹扩展距离或载荷循环次数确定裂纹扩展几何并再次重新划分裂纹网格，如此反复，便可得到裂纹每一步扩展的应力、SIF以及扩展寿命的详细数据。具体的疲劳裂纹扩展仿真模拟流程如图1所示。

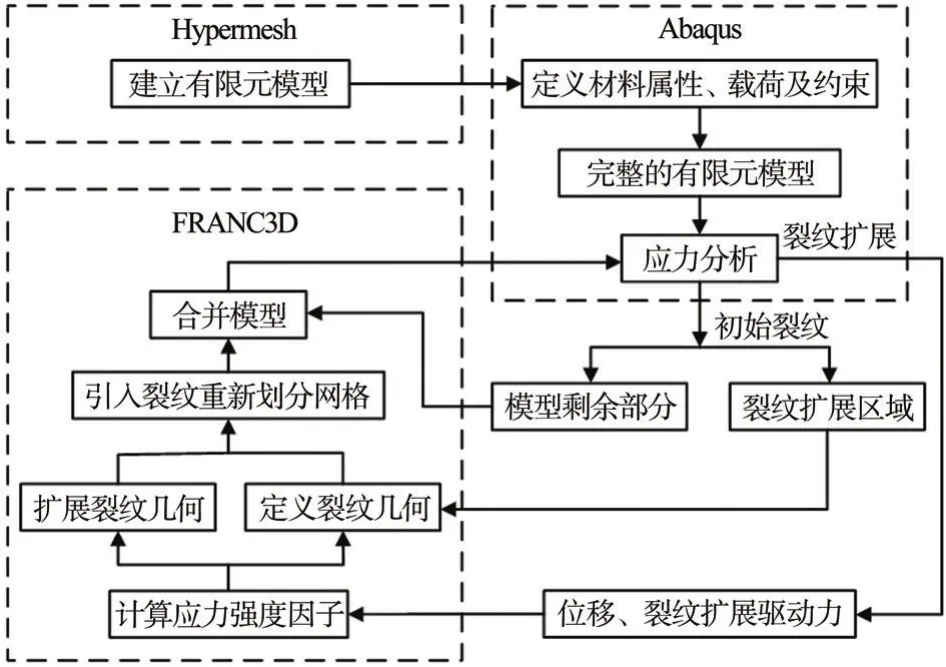
图1 疲劳裂纹扩展分析的具体流程Fig.1 Specific flow of fatigue crack propagation analysis

2 疲劳裂纹扩展过程

对裂纹进行疲劳裂纹扩展分析时需要确定三个重要参数，分别为局部裂纹扭转角度、局部裂纹扩展增量以及扩展后裂纹尖端的拟合外伸，如图2所示。

图2 裂纹扩展示意Fig.2 Schematic diagram of crack propagation

2.1 计算裂纹尖端局部扭转角度

通过Abaqus应力分析后，根据式（1）计算出裂纹尖端的SIF大小。

式中m取Ⅰ、Ⅱ、Ⅲ，分别表示三种裂纹类型；a为裂纹尺寸；F为与裂纹尺寸相关的系数。结合工程判据计算出裂纹尖端各个节点的偏转角度（见图2中的θ角）。其工程判据有最大张应力准则、局部对称原则、最大能量释放率准则以及最小应变能密度准则等，这些判据本质上相差不大，都是倾向于最小化Ⅱ型裂纹应力强度因子的准则，均可得到准确且相似的结果，本文采用最大张应力准则［5］，如图3所示，其裂纹偏转角θ计算公式见式（2）。

图3 最大张应力准则示意Fig.3 Schematic diagram of maximum tensile stress criterion

最大张应力准则的基本假设如下：

综上，通过此次PDCA循环法优化改进工作，我院住院药房药品调剂流程更加规范化，有效减少了领药次数和领药时间，提高了工作效率，形成了科学的管理制度和规范，最终形成长效机制，实现了对药品调剂流程的优化并且达到了持续改进的目的。

（1）裂纹沿最大周向应力σθmax的方向开裂；

（2）当此方向的周向应力到达临界值时，裂纹失稳扩展。

2.2 计算裂纹尖端局部扩展距离

得到裂纹尖端的扭转角后，还需确定裂纹尖端节点的扩展距离（见图2中的Δa），从而确定扩展后裂纹尖端的位置。但裂纹尖端各个节点的SIF大小不一致，裂纹扩展时各个节点的扩展距离也不一致，且裂纹尖端局部扩展距离是针对一个节点而言，为了确定所有节点的扩展距离，需要指定一个节点的扩展距离，其余节点扩展距离根据其SIF值与指定节点SIF的比值大小来确定。由于裂纹两端接近表面，局部不再保持平面应变条件［6］，计算出的SIF精度较差，为了减小误差，通常指定的节点都选取为裂纹中部且SIF值接近于平均应力强度因子的节点，其扩展距离为 Δamid，其余节点Δa由式（1）确定。

2.3 扩展后裂纹的拟合及外伸

扩展后的裂纹尖端由各节点扩展后的位置连接确定，但直接相连接会形成锯齿形裂纹尖端（如图2中的蓝虚线所示），形成数值“噪音”，这种非光顺的裂纹在下一步裂纹扩展计算出的SIF曲线也是锯齿形的，导致后续裂纹扩展极其不稳定。为了消除数值“噪音”的影响，需要对每一步扩展后的裂纹尖端进行光顺化处理（如图2中红实线所示）。

3 裂纹扩展增量对裂纹扩展稳定性的影响

在指定裂纹尖端局部扩展距离时，有以下两种确定方法。

（1）指定载荷循环次数来推算。

根据指定的载荷循环次数来推算出裂纹扩展距离，但指定的载荷循环次数在裂纹扩展初期可能偏小，导致扩展距离步过小，计算时间加长，效率低。而对于裂纹扩展后期而言又可能过大，裂纹扩展过快导致失稳断裂。

（2）指定扩展增量计算。

指定的扩展增量若过小，裂纹扩展过程会较为缓慢，计算时间虽然加长，但裂纹前缘相对比较稳定。若裂纹扩展增量过大，由于裂纹两端的SIF值精度较低，会加剧裂纹两端与中间部分扩展增量的差值，造成裂纹的不稳定扩展。

图4 CT试样外形尺寸参数Fig.4 Contour dimension parameter diagram of CT sample

在Hypermesh中构建有限元网格模型如图5所示，随后导入Abaqus中定义载荷及约束条件，分别将上、下加载孔心与其孔表面耦合在一起，对上加载孔心施加6 kN向上的拉力，对下加载孔孔心的XYZ位移及其转动全部约束住。

图5 CT试样有限元网格模型Fig.5 Finite element mesh model of CT samples

材料选取为低碳钢Q235，参考董达善［8］和赵章焰［9］等用三点弯曲试验测定的Q235钢材料的疲劳裂纹扩展性能参数，得到材料断裂参数C、m、应力强度因子阀值ΔKth以及断裂韧性KC如表1所示。

表1 低碳钢Q235材料参数Table 1 Material parameters of low carbon steel Q235

在Abaqus中提交应力分析后导入FRANC3D软件中，在CT试样缺口处预设一条长8 mm的贯穿裂纹并重新绘制局部裂纹网格，得到如图6所示的初始裂纹尖端应力分布。

图6 CT试样初始裂纹尖端应力分布Fig.6 Stress distribution at the initial crack tip of the CT sample

根据GB/T 6398-2017标准规定，设置其应力比R=0.1，分别在0.2 mm、0.5 mm、1.0 mm、1.5 mm以及2.0 mm的裂纹扩展增量（Δa）情况下对裂纹进行扩展分析，得到每种情况下的裂纹扩展如图7所示。

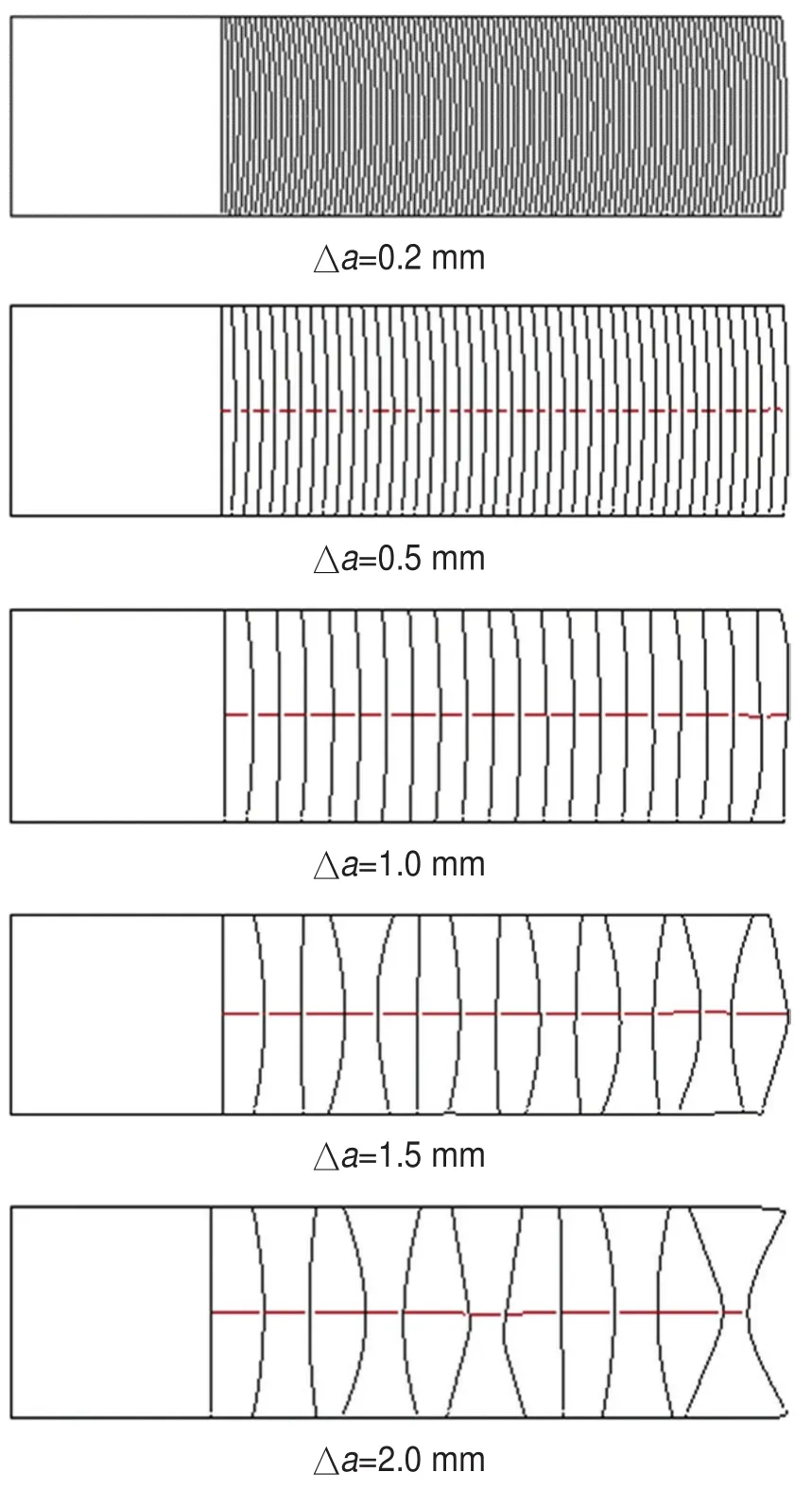
图7 不同裂纹扩展增量的裂纹扩展示意Fig.7 Schematic diagram of crack growth at different crack growth increments

为了比较在不同Δa情况下的裂纹扩展状况的好坏，将裂纹扩展过程中裂纹尖端中部SIF值的稳定性作为评估标准，GB/T 6398-2017标准中给出了CT试样SIF值的计算公式［10］如式（2）所示，将其计算结果作为理论参考值。

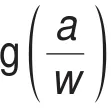
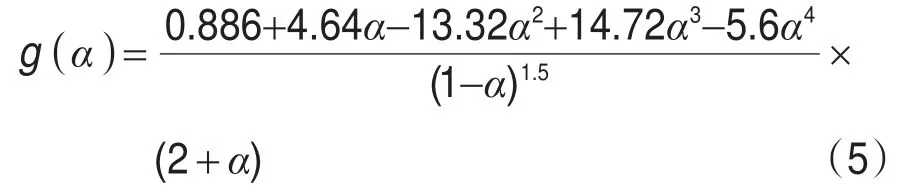
需要注意的是，标准中公式计算出的理论SIF值代表整个裂纹尖端的值，即认为CT试样贯穿裂纹的裂纹尖端SIF值处处相等。而在实际仿真计算中，贯穿裂纹两端为自由表面，靠近两端的裂纹尖端逐渐趋向于平面应力状态，中间内部裂纹处于平面应变状态，使得实际仿真计算出的CT试样贯穿裂纹SIF值会出现两端小、中间大的情况，长8 mm的预制裂纹尖端SIF值及在Δa=2.0 mm时后续4步裂纹扩展过程与理论参考值的比较如图8所示。

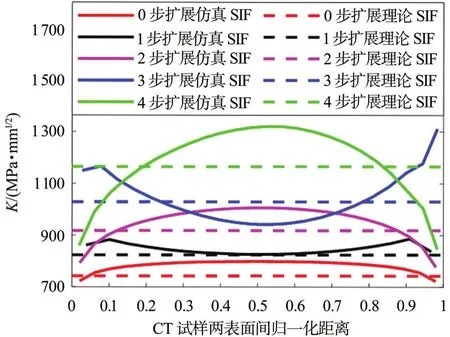
图8 CT试样长8 mm预制裂纹尖端SIF值及其理论参考值Fig.8 SIF value and its theoretical reference value of 8 mm prefabricated crack tip of CT sample

由图7可知，Δa=0.2 mm、Δa=0.5 mm以及Δa=1.0 mm时，每一步扩展拟合后的裂纹尖端形状都比较平稳，裂纹扩展过程稳定；Δa=1.5 mm以及Δa=2.0 mm时，裂纹扩展尖端明显趋向凸凹状，扩展极其不稳定，甚至在扩展后期由于裂纹尖端形状异常导致重新引入裂纹网格的困难，无法进行下一步扩展分析，需要修正裂纹尖端的拟合形状。由图8可知，贯穿竖直裂纹尖端中部SIF大、两端SIF小，导致在扩展时中部扩展距离长、两端短，形成凸状裂纹尖端。而凸状裂纹尖端两端SIF大、中间SIF小，导致在扩展时两端距离长、中间短，若扩展增量合适，裂纹尖端会重新形成竖直贯穿裂纹（见图7中Δa=1.0 mm）；若扩展增量较大，则会形成凹状裂纹尖端（见图7中Δa=2.0 mm）。

为弱化裂纹两端SIF值的影响，选取裂纹尖端中部计算结果为评估值，其与理论计算结果的误差为7.59%，主要来源于标准给出的理论计算公式中假定了CT试样为刚性体，未考虑外加载荷和边界条件带来的影响［11-12］。而仿真计算时为了提高计算精度，在裂纹尖端还设置了三圈奇异单元环，使得理论计算结果要小一些，与实际结果存在一定偏差。将不同扩展增量下每一扩展步的SIF结果与理论计算结果进行比较，如图9所示。

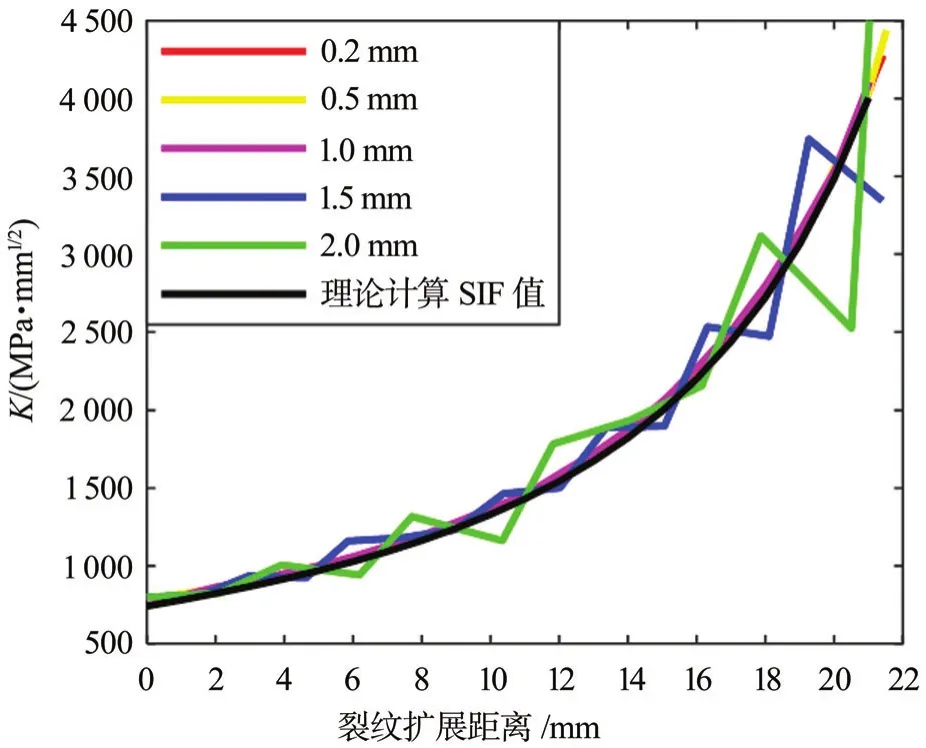
图9 不同扩展增量下每一扩展步的SIF结果与理论计算结果Fig.9 SIF results and theoretical calculation results of each expansion step under different expansion increments

由图9可知，在小的裂纹扩展增量情况下，裂纹中部尖端SIF值与理论参考值接近重合，存在一定可接受范围内的误差，随着扩展增量的加大，尤其是在Δa=1.5 mm和Δa=2.0 mm时，裂纹扩展变得逐渐不稳定，呈现凸凹状，且SIF值也在理论参考值附近波动；在Δa=0.2 mm和Δa=0.5 mm时，裂纹扩展平稳，计算结果与理论值也相差不大；Δa=1.0 mm的裂纹扩展后期逐渐出现不稳定扩展趋势。为了在保证计算精度的前提下需尽可能减少计算时间，根据本文数据可知，裂纹扩展增量Δa=0.5 mm时裂纹扩展稳定、计算时间短并且计算精度高。本文模型的裂纹尖端单元特征尺寸为2 mm，结合管建东［12］的网格参数对FRANC3D软件计算SIF精度的影响研究，裂纹扩展增量选取为当前裂纹尖端单元特征尺寸的15%～30%比较合适。

4 结论与展望

本文通过利用FRANC3D和Abaqus软件联合仿真分析了Q235钢CT试样在不同裂纹扩展增量情况下的裂纹扩展稳定性，得出了以下结论：

（1）在实际仿真计算中，贯穿裂纹两端为自由表面，由于靠近两端的裂纹尖端逐渐趋向于平面应力状态，中间内部裂纹处于平面应变状态，导致应力强度因子SIF呈现中间大、两端小的对称分布，进而使得裂纹扩展时中间部分裂纹尖端扩展距离长，形成凸状裂纹尖端。凸状裂纹尖端中间SIF小、两端大，在大的裂纹扩展增量情况下裂纹形成凹状裂纹尖端，凸凹交替的裂纹扩展极其不稳定，甚至会影响下一扩展步的网格划分。

（2）在进行裂纹扩展分析时，为保证计算精度和节约计算时间，并且保证裂纹扩展的稳定性，裂纹扩展增量选取为当前裂纹尖端单元特征尺寸的15%～30%比较合适。

本文研究的对象是标准拉伸试样，裂纹为贯穿裂纹，属于Ⅰ型裂纹扩展，而裂纹扩展增量对复合型裂纹扩展结构的影响未曾分析，还有待研究。