基于FTA和BP神经网络的网络系统故障诊断方法研究

李帅，张军

（哈尔滨师范大学 计算机科学与信息工程学院，黑龙江 哈尔滨 150025）

0 引言

在信息时代，随着各种信息技术不断创新与发展，计算机网络给人们带来了极大的方便与好处，但随之而来的是一系列网络安全[1]问题。网络安全问题不仅关乎个人的财产安全，更关乎群体利益乃至国家的稳定发展，在这个新型的互联平台，守护平台和谐稳定，共建美好网络环境是每一个人的共同责任。为了保证网络系统的安全性和稳定性，学者们对此进行了大量的研究。随着网络吞吐量和安全威胁的不断增加，入侵检测系统（IDS）[2]的研究受到了计算机科学领域的广泛关注。当前反复无常的入侵类别不仅对入侵防御系统构成挑战，而且对其庞大的计算能力构成挑战。LIAO等[3]针对当前存在的入侵防御检测系统的研究给出了一个详尽的图像进行全面的综述，表达出每种技术都有其优越性和局限性，而且学习算法在安全和隐私方面有较高的成功率，也为之后的学者们将机器学习的技术融入网络安全中提供了重要依据。

风险分析是软件开发的一项重要活动，做得好可以确保关键资产以安全可靠的方式运行。故障树分析法（Fault Tree Analysis，FTA）是其中最突出的技术，被各行业广泛使用。FLAGE等[4]应用了一个综合概率可能性计算框架，将认知的不确定性联合传播到故障树的基本事件的概率值上，并使用可能性概率转换在纯概率和可能性设置中传播认知不确定性。将不同方法的结果与顶部事件概率的不确定性表示进行比较，这个方法的提出有助于分析人员有效地应对新兴技术带来的安全挑战。

反向传播（Back Propagation，BP）神经网络具有良好的自学习能力、自适应能力和泛化能力。QIU等[5]针对传统BP神经网络入侵检测模型在检测率和收敛速度方面的缺陷，结合粒子群优化算法（Particle Swarm Optimization，PSO）将改进的PSO-BP神经网络应用于入侵检测系统模型中，分析了梯度下降算法和附加动量算法，验证了系统在假负率、假阳性率和收敛速度方面的改进效果，为网络安全的未来发展提供建设性的建议，值得在实践中进一步推广。

1 网络系统故障诊断分析模型

1.1 网络系统故障FTA模型

网络系统故障FTA模型本质是将网络系统故障作为顶事件，逐层分析其可能引发顶事件的一系列原因，通过与门操作符和或门操作符将各事件之间的逻辑关系建立逻辑连接，最终生成一张倒立的树状逻辑因果关系图。

1.2 BP神经网络模型

BP神经网络是一种梯度下降方法，通过网络计算将输入层的值分别传输到隐含层和输出层，将最终输出值与样本值进行比较，计算误差。BP算法是一种误差函数按梯度递减的学习方法[6]，图1显示了这样一个网络。在这个网络中，有一个输入层、一个输出层，以及它们之间的一个或多个隐含层。三层BP神经网络结构如图1所示。

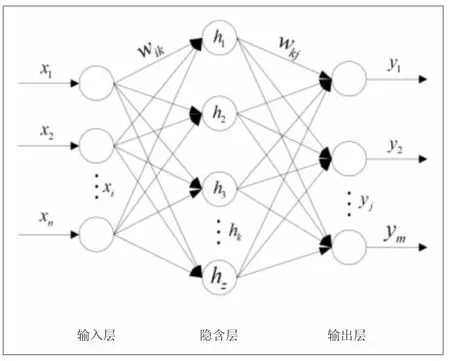
图1 三层BP神经网络结构图

根据BP神经网络的特性，只需具备单层隐含层和有限数量的神经单元，就能以任意精度拟合任意复杂度的函数。那么，若用表示输入层的集合，其输入层的集合表示如下：

其中，x表示输入层，h表示隐含层，i表示输入层的次序数，k表示隐含层的次序数，wik表示输入层第i节点到隐含层第节点的权值，若用hk表示隐含层的输出，其隐含层的输出表示如下：

其中，f1表示输入层到隐含层的传递函数，f2表示隐含层到输出层的传递函数，θ是隐含层的阈值。

与传统的BP神经网络不同，在激活函数部分进行了改进，由于Sigmoid的收敛比较缓慢，并且Sigmoid函数是软饱和，所以容易产生梯度消失的问题。根据不同的情况混合使用Sigmoid函数、Softsign函数和ReLU函数用来改善单一函数所存在的一些问题（图2）。

图2 BP神经网络传递函数图像

从Sigmoid函数图像上可以看出，当神经元输出接近1时，曲线变得非常平缓，此时的导数也趋近于0，输出层饱和，收敛速度开始变慢，容易产生梯度消失。而softsign函数图像也是“S”形函数，不同的是Sigmoid函数的取值范围是[0，1]，而Softsign函数的取值范围是[-1，1]，从图2可以看出，Softsign函数图像相对于Sigmoid函数图像而言过渡得更加平滑，而且解决了Sigmoid函数以非0为中心的问题，但是梯度消失的问题仍然没有解决，因此引入ReLU函数，与Sigmoid函数和Softsign函数相比，ReLU函数不会在正数的区域产生饱和现象，有效解决了梯度爆炸和梯度消失的问题，并且ReLU函数的效率更高，收敛速度更快，而且ReLU函数的特点是会使其中一部分的神经元输出为0，那么就会促使网络变得稀疏，并且减少参数之间的相互依存关系，从而达到缓解过拟合的问题。在BP神经网络中激活函数并不是唯一的，但根据情况选择合适的激活函数是有必要的，对于图2中的3种函数的优缺点进行自由混合，利用其优势解决相应问题，这样可以在设计学习模型时减少网络的参数和隐含层的节点数量，简化结构，有效提高泛化能力。

在学习模型的训练过程中，关键是通过损失函数计算学习的误差及确定模型的可靠性。假设Tj是输出层y上第j节点的期望输出，那么损失函数e表示如下：

2 实例研究

2.1 数据集采集

采用FTA-BP故障诊断模型对网络系统故障中网络入侵[7]分支进行分析实验。本次实验选用的数据集是第三届国际知识发现和数据挖掘工具竞赛使用的KDD CUP 99数据集，选取总计500条样本用于本次实验。其中，400条为正常流量，100条为异常流量。次序随机打乱，随机选择400条作为训练数据，100条作为测试数据进行实验。

2.2 性能指标

在损失函数的基础上将均方误差（MSE）[8]作为FTA-BP模型的误差输出函数，用于测试该模型的性能。均方误差不仅可以减少整个训练集的全局误差，而且可以降低每个特定样本输入时的局部误差，并通过BP神经网络不断学习，不断调整更新权值和阈值，从而不断降低误差，使实际输出越来越接近期望输出。均方误差MSE表示如下：

其中，w表示权值，θ表示阈值，80%n表示输入层全部样本的80%为训练样本，20%为测试样本。通过把得到的均方误差不断向前反馈，进行多次迭代采用，广义的感知学习规则不断更新权值和阈值[9]，直至算法达到预期的效果为止。本研究基于梯度下降法，以目标的负梯度方向对参数进行更新，对均方误差MSE（w，θ）给定学习率η，计算均方误差对于权值部分的变化率进行调整，那么遵循反馈神经网络误差不断减小的原则，权值的调整量△wik和△wkj分别表示如下：

同样的，计算均方误差对于阈值部分的变化率进行调整，那么遵循反馈神经网络误差不断减小的原则，阈值的调整量△θik和△θkj分别表示如下：

2.3 数据预处理

该数据并不是统一的数字数据类型，还有其他的一些字符特征描述，如果随意将字符数据丢弃，将会导致预测结果出现偏差。所以本研究通过Python Pandas中的Transform函数对文本信息进行字符特征向数字特征转换，即对该数据集中的文本数据类型转化为BP神经网络训练使用的数字数据类型。

2.4 实验结果

通过FTA-BP模型对KDDCUP 99数据集进行了多次预测训练，最佳FTA-BP实验结果如图3所示。

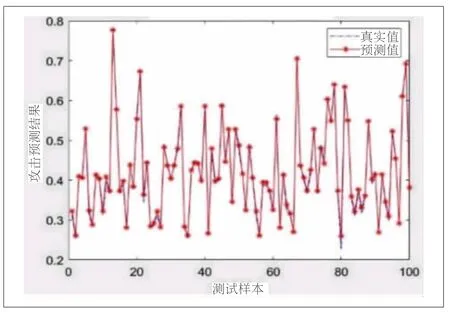
图3 FTA-BP模型攻击预测结果

实验确定了最佳的隐含层节点个数为9，相应的均方误差为2.7298×10－5，准确率为96.51%。训练结果显示验证性能在第96轮时表现最佳。

3 结语

在传统BP神经网络的基础上，结合故障树分析法对传统BP模型进行了改进，提出了一种FTA-BP网络系统故障诊断模型。通过仿真实验分析，提出的FTA-BP网络系统故障诊断模型相比传统的BP模型和ELM模型具有明显的优势，不仅提高了模型的精确率，而且预测效果较稳定。信息时代面临尤为重要的网络安全问题，网络系统故障诊断方法是必不可少的。该模型还存在着一定的缺陷，虽然预测的准确率比传统的BP模型要高，但是平均准确率还未达到最高标准。而且，实验选用的数据集也存在着一定的局限性。下一步需要解决的问题是如何将FTA-BP模型的精确度进一步提升及如何将FTA-BP模型应用在网络系统故障的其他部分。