MPVCC问题的M稳定性的序列最优性条件研究

许 娜， 姜 姗， 沈 洁

(辽宁师范大学 数学学院，辽宁 大连 116029)

本文主要研究带有垂直互补约束的数学规划 (Mathematical program with vertical complementarity constraints) 问题，简称MPVCC，

minf(x)
s.t. min{Fk1(x),Fk2(x),…,Fkl(x)}=0,k=1,…,m,g(x)≤0,h(x)=0.

其中，f：n→,g：n→p,h：n→q,Fki：n→(k=1,…,m,i=1,…,l)是连续可微函数.

MPVCC问题在工程设计、交通运输、通信与管理等许多领域都有着广泛的应用,因而研究该问题具有重要的理论意义和实际价值.由于垂直互补约束的特殊结构，往往不能直接用非线性规划的理论结果来研究MPVCC问题．在2000年，Scheel和Scholtes[1]提出了MPVCC问题的C-,B-,S-稳定性条件.基于上述研究工作，梁彦超等人[2]给出了MPVCC的M-稳定性条件. 2013年,张杰等人[3]给出了一种求解MPVCC问题的正则化方法，然后讨论了MPVCC问题的常用约束规范,例如：MPVCC-CRCQ,MPVCC-CPLD,MPVCC-rCPLD等约束规范[4].

基于序列最优性条件在算法的收敛性分析和数值表现等方面的重要应用, Andreani等人[5]和Ramos[6]给出了带有互补约束的数学规划(MPCC)问题的序列最优性条件.本文给出了比MPCC问题更一般的MPVCC问题的序列最优性条件,即AM稳定性. 然后, 给出与MPVCC问题的AM稳定性相关的AM正则性，证明了MPVCC问题的局部最优解在AM稳性条件下是M稳定点，这说明了AM正则性是一种能够保证M稳定性的约束规范. 最后，讨论了AM正则性与其他的MPVCC约束规范的关系．

1 基础知识

本节给出文中需要用到的一些基本概念.

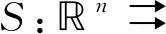
∇Fki(x*)Γki=0,k=1,…,m,i=1,…,l,g(x*)Tλg=0,

当Fki(x*)=Fki′(x*)=0时,或者Γki>0,Γki′>0或者ΓkiΓki′=0.

下面给出指标集的定义，对于一个给定的MPVCC问题的可行点x*，令

Ig=Ig(x*)={i|gi(x*)=0},

K(x*)={k∈{1,…,m}|∃i,j,i≠js.t.Fki(x*)=Fkj(x*)=0},

Jk(x*)={i∈{1,…,l}|∃i,j,j≠i,Fki(x*)=Fkj(x*)=0},

定义1.4[4](MPVCC-rCPLD)设x*是MPVCC问题的一个可行点，{∇hi(x*),i∈Ih}是空间span{∇hi(x*),i=1,…,q}的一组基，称MPVCC松弛正线性约束规范(MPVCC-rCPLD)在x*点处成立，如果存在x*的邻域N(x*)使得

(1)对任取的x∈N(x*),{∇hi(x*),i=1,…,q}有相同的秩;

(2)对∀J0⊂Ig,∀K0⊂IF(x*),若

{ ∇gi(x*),i∈J0},{∇hi(x*),i∈Ih},{ ∇Fij(x*)=0,(i,j)∈K0}

是正线性相关的,那么对于每个x∈N(x*),

{∇gi(x),i∈J0},{∇hi(x),i∈Ih},{∇Fij(x)=0,(i,j)∈K0}

是线性相关的.

2 关于M稳定性的序列最优性条件

本节给出了关于MPVCC问题M稳定性的近似条件(AM稳定性)的定义，并证明AM稳定性条件是一个合理的序列最优性条件.显然，AM稳定性条件有助于MPVCC算法的收敛性分析.

定义2.1(AM稳定点)MPVCC的可行点x*是近似M稳定点(AM稳定点),如果存在序列{xt}⊂n和,k=1,…,m,i=1,…,l,使得

(1)

(2)

(3)

(4)

(5)

为了证明AM稳定性条件是序列最优性条件，MPVCC问题写为下述带有几何约束的形式

(6)

定理2.2假设x*是MPVCC问题的局部最优解,则x*是AM稳定点.

(7)

令(xt,zt)是问题(7)的全局最优解，接下来证明{(xt,zt)}→(x*,Φ(x*)),由于(xt,zt)是全局最优解，所以得到

(8)

整理得

由文献[6]中定理6.12得到

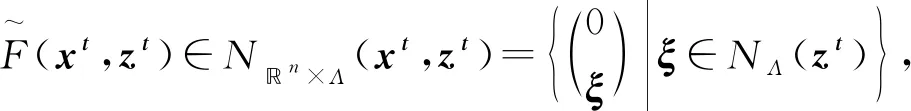
其中，

其中，γt=(γg,t,γh,t,γF,t)∈NΛ(zt),zt=(zg,t,zh,t,zF1,t,…,zFm,t),

所以式(3)成立.

进而有

所以式(4)和式(5)成立,综上所述x*是AM稳定点.

3 保证M稳定性的新的约束规范

衡量序列最优性条件的一种方法是将其与精确的稳定性联系起来. 也就是说，需要研究在MPVCC问题的约束规范下，证明AM稳定点就是M稳定点. 为此，首先给出与MPVCC问题的AM稳定性相关的AM正则性，然后证明了AM正则性实际上是一种能够保证M稳定性的新的约束规范．最后，基于上述结果， 比较AM正则性与MPVCC-rCPLD、MPVCC-CCP约束规范的关系，可以得到AM正则性是一个非常弱的约束规范．

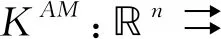
定理3.2假设x*是MPVCC问题的一个可行点,AM正则性在x*处成立当且仅当对于任意连续可微的目标函数,x*是AM稳定点就意味着x*是M稳定点.

证(必要性)令f是一个连续可微的函数,x*是AM稳定点,存在一个序列{xt}⊂n且,k=1,…,m,i=1,…,l.由于以下两个式子成立

(9)

再由

可推出

其中,

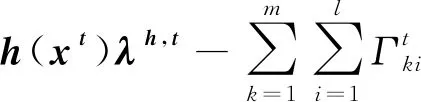
(10)

由AM正则性可知，

所以x*是MPVCC问题的M稳定点.

由定理2.2和定理3.2，可以得到下面的结果．

推论3.3假设x*是MPVCC问题的一个局部最优解,如果AM正则性在x*点处成立，则x*是M稳定点.

该结果意味着AM正则性确实是关于M稳定点的约束规范，下面将比较AM正则性与其他的MPVCC约束规范的关系．

定理3.4假设x*是MPVCC问题的一个可行点,如果MPVCC-rCPLD约束规范在可行点x*处成立,那么AM正则性在x*点处也成立.

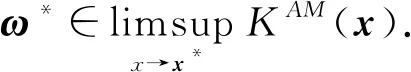
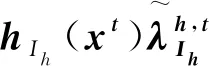
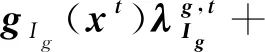
(11)

(12)

定义3.5假设x*是问题(6)的可行点，如果集值映射n×Λ∇Φ(x)TNΛ(z)在(x*,Φ(x*)) 点处是外半连续的,即

则称MPVCC锥连续性(MPVCC-CCP)约束规范在x*点处成立.

定理3.6假设x*是MPVCC问题的一个可行点,如果AM正则性在x*点处成立，那么MPVCC-CCP约束规范在x*点处成立.

证如果AM正则性在x*点处成立,由定理3.2可知,若x*是AM稳定点,能推出x*是M稳定点，令

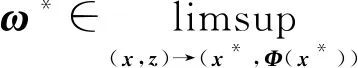
则存在序列{xt},{ωt},{γt}和{zt}使得

xt→x*,zt→Φ(x*),ωt=∇Φ(xt)Tγt→ω*,

其中,zt=(zg,t,zh,t,zF1,t,…,zFm,t),γt=(γg,t,γh,t,γF,t)∈NΛ(zt),

下面验证

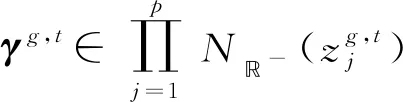
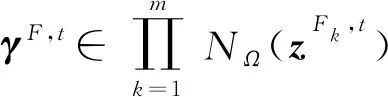
定义f(x)=-(ω*)Tx,则有∇f(xt)+ωt=-ω*+ωt→0,可知x*是AM稳定点，由定理3.2可知x*也是M稳定点,可以推出

所以MPVCC-CCP约束规范在x*点处成立.

4 小 结

本文主要研究了MPVCC问题的序列最优性条件，得到了MPVCC问题的AM稳定性条件，并证明AM稳定性条件是一个合理的序列最优性条件. 然后，给出与MPVCC问题的AM稳定性相关的AM正则性，并证明了AM正则性实际上是一种能够保证M稳定性的新的约束规范．最后，比较了AM正则性与其他的MPVCC约束规范的关系．