基于子模型法的盾构隧道纵向接头地震力学特性研究
2022-04-01郭翔宇廖峻斌张艳阳
耿 萍,郭翔宇,王 琦,廖峻斌,何 川,张艳阳
(1.西南交通大学 交通隧道工程教育部重点实验室,四川 成都 610031;2.中建壹品投资发展有限公司,四川 成都 610031)
盾构隧道是由管片及连接螺栓组成的装配式结构,在地震荷载作用下纵向接头会发生往复的拉压变形。因此,盾构隧道纵向接头往往是震害的高发区,产生管片的拉压破坏、螺栓的剪断及接缝的渗漏水等震害[1-3]。
现有研究多集中于盾构隧道横断面的抗震性能,对盾构隧道纵向地震响应特性的研究较少,且多集中于理论分析、数值模拟及部分试验方面。刘学山[4]将盾构隧道简化为一维杆系,将其周围的土体看作是黏弹性材料,将隧道纵向抗震简化为黏弹性地基中弹性杆系的振动问题。耿萍等[5]考虑轴力和弯矩共同作用对盾构隧道纵向弯曲变形的影响,在经典的志波模型基础上建立盾构隧道纵向等效抗弯刚度计算模型。邵润萌等[6]将盾构隧道简化为与其纵向变形一致的等价梁,采用反应位移法进行盾构隧道纵向弹塑性地震反应分析,结果显示输入角度和输入地震动水准是纵向抗震分析的重要影响因素。张景等[7]采用振动台试验方法研究穿越软硬突变地层盾构隧道纵向地震响应规律,结果表明:软硬突变地层不仅增大了隧道纵向内力,而且改变了其纵向整体弯曲方向。禹海涛等[8]考虑不同地震动输入方向、不同地震动类型等因素,开展盾构隧道-工作井节点振动台模型试验,结果显示地震作用下盾构隧道-工作井节点会使工作井模型产生较大环向应变,但不会造成节点处盾构隧道模型的环向变形增大。
以上研究成果多集中于合理的盾构隧道纵向模型化方法,或采用模型试验的方式研究接头受力变形特征。但由于建模方法或试验相似比的限制,无法表征纵向接头细部的具体受力形态。本文基于子模型分析方法,依托实际工程分析了纵向接头的受力危险区,进而以足尺试验的方式研究危险区的分布及破坏形态。
1 子模型法
盾构隧道沿纵向弯曲时,纵向接头在环向会受到所处管片环相邻管片的支撑与约束[9],即需考虑环向边界对纵向接头受力与变形的影响,见图1。

图1 环向边界受力特征
为考虑环向边界的影响,采用子模型法对接头细部进行分析。子模型法是一种基于有限元法的分步分析方法,首先建立网格及几何特征较粗糙的全局模型,然后建立关键区域的精细子模型,将全局模型中对应驱动节点处的位移值作为子模型的附加边界条件[10-12]。
以平面四边形单元模型为例,见图2,对位于单元内部的子模型驱动节点i的位移,可采用单元的四个节点j对其进行插值,见图3[13]。
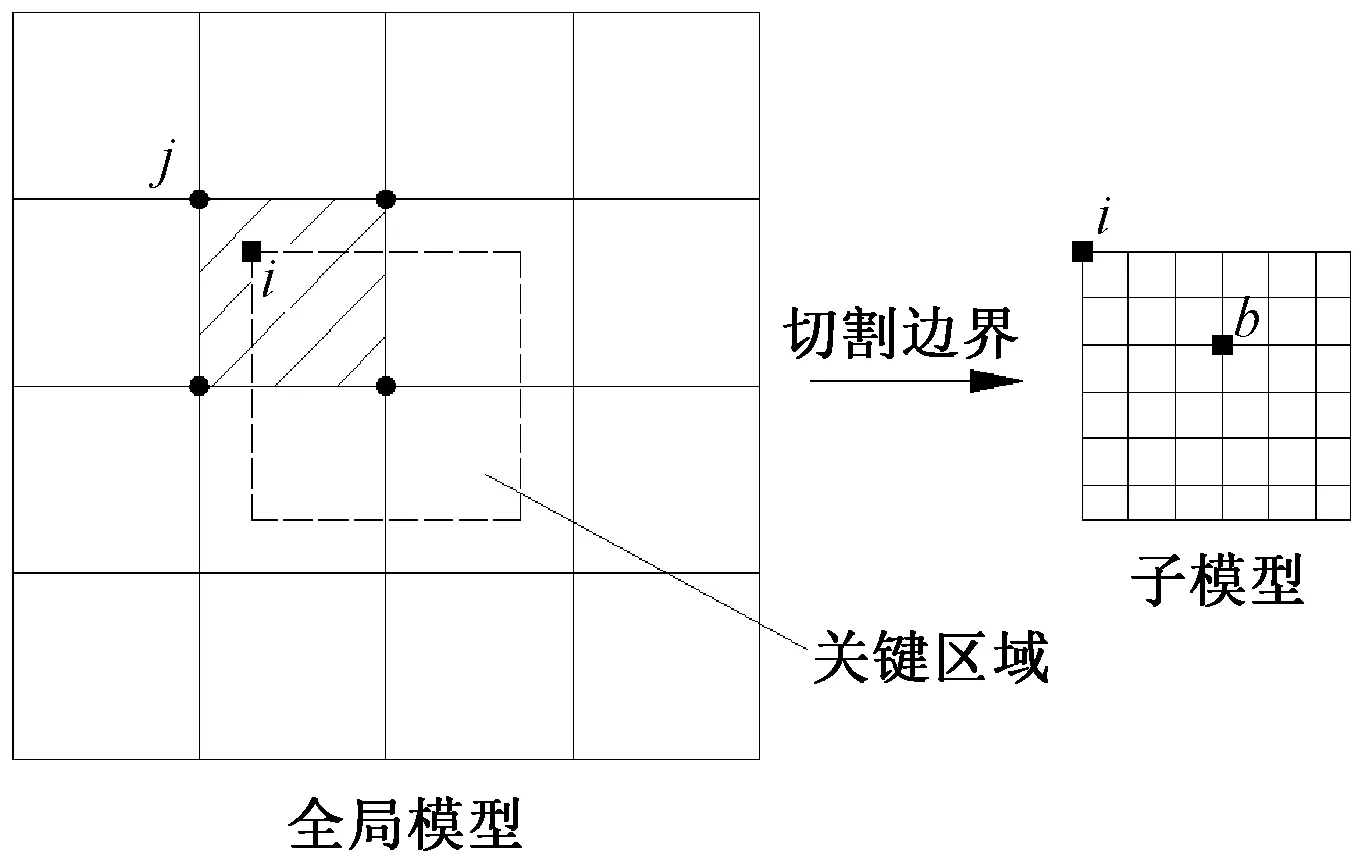
图2 子模型方法[10-12]

图3 全局模型单元
则四边形全局模型单元的形函数为[13]
(1)
式中:Nj为全局模型单元的形函数;ξ、η为全局模型单元节点j的坐标。
子模型驱动节点i在t时刻的位移为[13]
δi(t)=[δix(t)δiy(t)]T
(2)
式中:δi(t)为子模型驱动节点i在t时刻的位移。
使用形函数对位移进行插值,有[13]
(3)
式中:δj(t)为整体模型中节点j的位移矩阵。
动力有限元基本方程为[14]

(4)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;δ(t)为节点位移矩阵;F为荷载矩阵。
则有[14]
(5)
对式(5)整理得
(6)
式中:i、j、b分别为切割边界上节点、子模型外全局模型节点、子模型内节点。
由式(6)可知,子模型驱动节点的位移,是求解子模型内部节点位移平衡方程的荷载项的一部分。
2 全局模型分析
对于子模型法,最关键的是经由全局模型获取切割边界的位移。一般而言,子模型法的全局模型只有一个[15-16],但由于盾构隧道纵向较长,建立考虑盾构隧道纵向接头的整体模型进行复杂地层条件下的三维动力时程分析计算成本过高。在此为尽量简化模型,提高计算效率,设立两个全局模型:①基于“等效刚度梁-地层模型”获取环间内力;②将获取的环间内力施加到“纵向整体模型”上,得到子模型所需要的切割边界上的位移。其具体过程如下:对“等效刚度梁-地层模型”输入地震荷载,获取环间内力;将环间内力施加在“纵向整体模型”的纵向,得到整体模型各节点的位移;对“纵向整体模型”中的局部研究区域精细化建模,将整体模型切割边界上节点位移施加到精细化模型边界上。
2.1 基于纵向等效刚度梁模型的地震响应分析
隧道结构对地层振动具有明显的追随性[17-18],在此将盾构隧道考虑为追随地层变形的等效刚度梁[19]。本盾构隧道内径10.5 m,外径11.6 m,管片厚度55 cm,幅宽2 m。每环管片环分成8块,各块均采用C60钢筋混凝土浇筑。环间设有22根纵向斜螺栓,螺栓长度70 cm,直径40 mm,机械强度10.9级。管片采用错缝拼装,封顶块不位于拱顶及拱底[20],拱顶正中间未设置纵向螺栓。依照志波等效刚度理论,在此不考虑环间接头的预紧力[21],求得隧道纵向抗弯、抗拉及抗压等效刚度折减系数分别为0.069、0.027、1,以分别计算纵向弯矩、拉力、压力。
本盾构隧道为高压输电城市管廊工程,主要穿越第四纪淤泥质黏土、粉土、砂层等软弱覆盖层。依照实际工程建立三维地层模型见图4,模型尺寸为600 m×110 m×80 m(长×宽×高)。其中,盾构隧道穿越地层变化处。

图4 三维地层模型
土体采用弹性本构建模,地层物理力学参数见表1。

表1 物理力学参数
依照GB 50838—2015《城市综合管廊工程技术规范》[22]及GB 50223—2008《建筑工程抗震设防分类标准》[23],综合管廊工程结构设计使用年限应为100 a,按照乙类(重点设防)建筑物进行抗震设计。又高压电力隧道结构复杂,对纵向接头受力变形性能要求极高,需要进行专门的地震响应分析。依据场地地震安全性评价报告,100 a超越概率2%(罕遇地震)对应地震峰值加速度为0.213g,输入地震动见图5,据此分别计算隧道纵向接头在横向及纵向激励下的地震动响应。

图5 输入地震动(已基线校正)
从相关研究成果来看[7,24],当隧道穿越地层条件变化处时纵向内力最大。在此采用有限差分程序FLAC3D进行动力时程分析,在图4所示模型底部分别沿隧道横向及纵向输入图5所示地震动。依照相关研究成果[7,24],统计环间内力最大位置即盾构隧道穿越地层变化处的环间内力,结果见表2。

表2 穿越地层变化处纵向内力极值
由表2可知,当地震动沿隧道纵向激励时,隧道主要承受纵向拉压及水平弯矩;当沿隧道横向激励时,隧道受力以竖向弯矩为主。将表2中内力施加至 “实体管片-梁单元螺栓”纵向整体模型,可获得研究区域的边界位移。
2.2 纵向整体模型受力分析
叶飞等[25]研究成果显示,错缝及通缝拼装对盾构隧道纵向变形性能影响不明显。在此忽略盾构隧道的管片接头,在环向采用等效圆环模型,混凝土弹性模量折减系数取0.85,建立“实体管片-梁单元螺栓”纵向整体模型。模型共计10环,环与环之间采用梁单元螺栓连接,见图6。模型一端采用固定约束,另一端对模型施加纵向力。
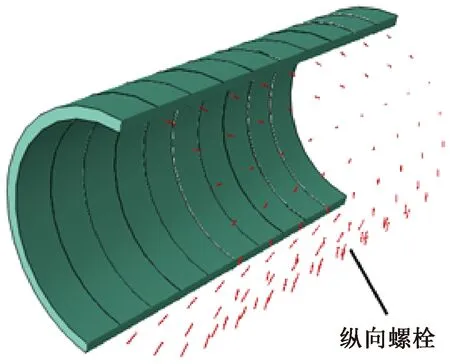
图6 纵向整体模型
沿横纵向激励时隧道受力特征不同,则需要考虑不同受力特征对隧道纵向局部的影响。相关研究成果显示,环间张开时接头受力更为危险[26],故在此仅考虑接头张开工况。显然,纵向激励时,“纵向受拉+纵向受弯”工况组合会在环间最大张开位置产生受拉危险区;横向激励时,“纵向受弯”会在受拉区的最外侧产生受拉危险区。不同条件下工况组合见表3。

表3 最不利工况组合
对纵向整体模型施加对应的力,可得到管片的受力状态,进而为局部细化模型提供相应边界条件。
3 局部细化模型分析
由于纵向螺栓位置及地震荷载下纵向受力特征不同,两种工况下的危险区域不尽相同。环间接缝面一共有22根纵向螺栓,认为接头张开时单根螺栓影响面积为管片环向的1/22,则每种工况均取管片环向的1/22建模,模型每侧长度取幅宽一半,即1 m,见图7。
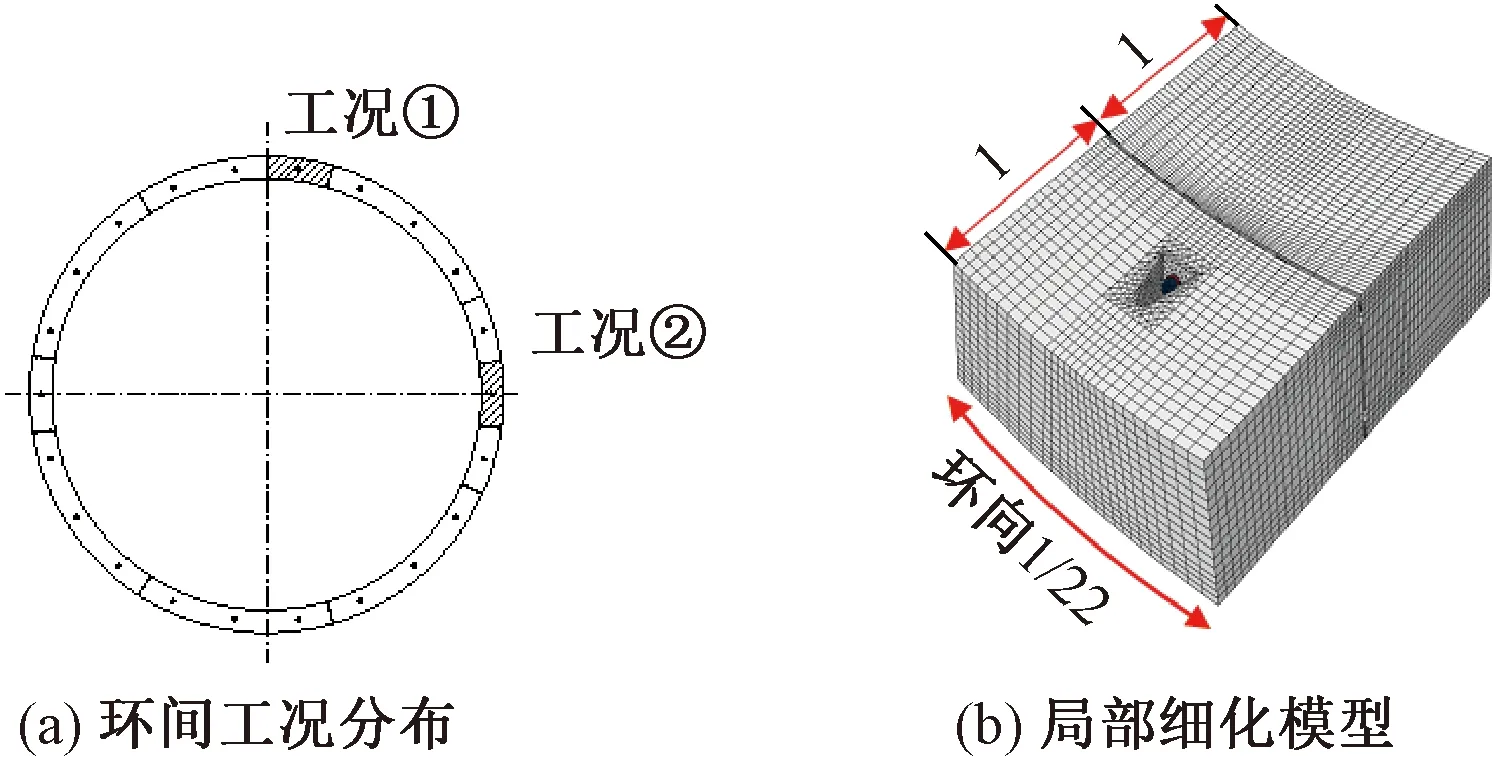
图7 局部细化模型计算工况(单位:m)
对于工况①,由于张开量最大位置(拱顶)没有纵向螺栓,接缝面顶部的拉力由两侧的两根对称螺栓所承担,在此选择其中一侧进行分析。
其中,管片结构采用C60混凝土弹性本构,螺栓采用双线性弹塑性本构,见图8。
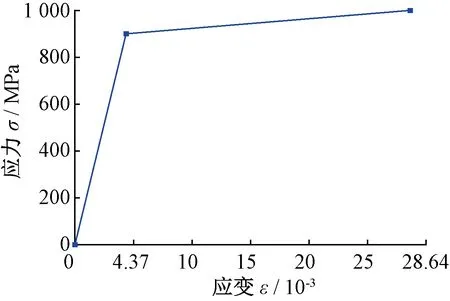
图8 螺栓双线性弹塑性本构
将图6各工况对应位置的边界位移施加到图7所示局部细化模型的切割边界上,即在切割边界上施加对应的边界位移。施加方法为:先将表3中所对应的拉力和弯矩施加到纵向整体模型(图6)中,计算完成后,提取边界节点位移施加到图7模型对应的切割边界上,则可以得到纵向不同状态下接头的受力变形特征。
显然,对于工况①、工况②而言,当环间接缝张开时,螺栓联合局部混凝土受力,则管片及螺栓的受力特征见图9、图10。

图9 工况① 结构受力(单位:MPa)

图10 工况② 结构受力(单位:MPa)
由图9、图10可知,当盾构隧道发生“纵向拉弯”及“纵向弯曲”时,其受拉区受力特征基本保持一致。
对于管片结构,其最大主应力主要分布于手孔、接缝面及套筒周边。手孔位置受到螺栓向外的拉力且几何形态不规整,在几何形态变化处出现明显拉应力区,两工况中手孔位置受拉区范围为手孔向管片内扩展40~50 mm深度。对于套筒周边而言,螺栓受拉即套筒有向外拔出趋势,套筒周边混凝土有较大拉应力区,两工况中套筒位置受拉区范围为套筒向周边扩展40~60 mm深度。套筒邻近管片外表面,极限状态下接缝面邻近外表面的区域更易破坏。斜螺栓两端被管片固定,斜螺栓可以传递剪力,在接头张开的过程中螺栓形态有趋向水平的趋势。此过程中,螺杆挤压接缝面混凝土,螺杆伸长过程中在摩擦力的作用下接缝面混凝土被向外牵引,出现部分拉应力区。
对于螺栓而言,其两侧固定且形态有趋向水平的趋势,则伸长过程中在靠近套筒及手孔位置螺栓会发生弯曲,即螺杆上出现两处应力集中区。
对比工况①、工况②的应力极值,管片结构最大主应力均位于套筒周边混凝土上,工况①(4.12 MPa)>工况②(2.30 MPa);螺栓最大应力出现在邻近套筒口的螺杆上,工况①(25.80 MPa)>工况②(13.20 MPa)。从管片及螺栓应力极值可见,对于纵向接头,其在地震荷载纵向激励下更加危险。工况①纵向弯矩(0.054 2 MN·m)远小于工况②纵向弯矩(1.45 MN·m),但其受力却更加危险,这说明对于纵向接头,纵向轴力对其受力起主导作用。
考虑边界位移带来的应力扰动,隐藏边界处若干层单元,提取管片结构内外表面邻近接缝面位置沿隧道纵向的应力及纵向接头张开量。
提取计算结果时,以接缝面螺栓孔处为坐标轴原点,以沿盾构隧道径向为坐标竖轴,以管片内外表面的实际长度(弧长)为横轴(计算观测点位置),则管片表面邻近接缝面位置沿隧道纵向的应力分布形式见图11。
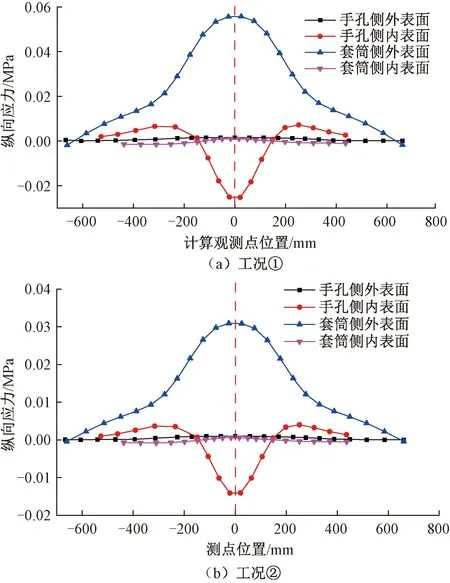
图11 受拉区管片表面纵向应力
由图11可知,盾构隧道发生“纵向拉弯”及“纵向弯曲”时,管片表面纵向应力分布特征基本一致。
手孔侧管片外表面分布有广泛的拉应力区,而内表面中部有较大的压应力区,向两侧逐步变为拉应力,这是由于接头张开过程中螺栓头挤压管片所导致。套筒侧管片由于内表面距离螺栓锚固端较远,故应力较小,而外表面距离螺栓锚固端较近,在套筒带动周边混凝土受拉过程中,外表面表现出广泛的拉应力区。
对比管片内外应力,可见工况①表面最大纵向应力为0.056 MPa,远小于其最大主应力极值4.12 MPa;工况②表面最大纵向应力为0.031 MPa,远小于其最大主应力极值2.30 MPa。这说明盾构隧道在纵向受拉时,其拉应力危险区主要位于管片内部,对表面影响有限。
当盾构隧道纵向存在弯矩时,纵向接头张开量最大处位于管片外侧,提取工况①、工况②接缝面外侧接头张开量,见图12。
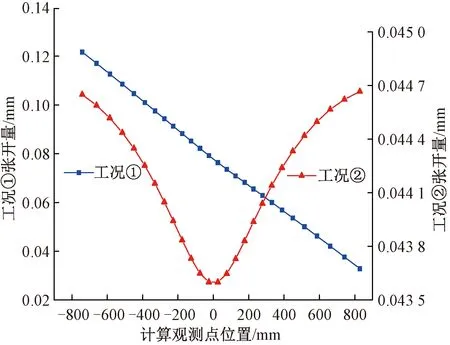
图12 纵向接头张开量
当盾构隧道遭遇纵向激励时,沿纵向有水平弯矩产生,由图7可知,工况①位于管片顶部的一侧,则接头在张开过程中纵向接头张开量出现非对称特征,最大张开量出现在管片拱顶。
隧道遭遇横向激励时,盾构隧道沿纵向发生水平弯曲,对照图7可知,工况②位于管片拱腰,且螺栓恰好位于水平线上,则张开量出现左右对称特征。又螺栓位于局部细化模型的正中间,在接头张开过程中邻近混凝土受到拉力较大,变形较为明显,故工况②模型中部张开量较小,向两侧逐步增大。
对比两种工况张开量最值,工况①(0.122 mm)>工况②(0.045 mm),可见纵向激励下盾构隧道纵向变形更加明显。
由图11、图12可知,对于工况①,其管片表面纵向应力为对称分布,而张开量呈现非对称特征,说明相对表面应力,接头变形对地震荷载更加敏感。
4 纵向接头破坏试验
由以上数值模拟研究成果来看,盾构隧道纵向接头承受地震荷载时,其薄弱部位位于管片内部,环绕套筒。在此采取破坏试验的方式研究纵向接头的受力变形特征。
当盾构隧道沿纵向承受纵向拉力时,纵向接头仅受拉。当盾构隧道纵向承受弯矩时,可由等效刚度梁模型[21]计算环间应力,公式为
(5)
式中:M为纵向弯矩;Is为管片横断面惯性矩;φ为表示中性轴位置的角度;x为中性轴至管片横断面应力计算位置的距离。
结合工程背景,管片厚度为0.55 m,可得受纵向弯矩时张开量最大处管片内外侧应力差Δσt=5.6%,相差较小,说明此处受弯效果不明显。由图9、图10可知,对于纵向拉力主导工况与纵向弯矩主导工况,张开量最大处管片及螺栓受力特征基本一致,即张开量最大区域在一定程度上可认为仅受拉力,故破坏试验中仅对管片施加纵向拉力。
由数值计算可见,纵向荷载作用下管片内受拉区为手孔或套筒向管片内拓展40~60 mm,影响范围相对较小。故试验采用C60混凝土足尺平直试件,手孔侧及套筒侧试验构件尺寸均为1 m×0.6 m×0.55 m(长×宽×厚)。试验构件设计详图见图13,共分为两部分:试验管片为试验端,进行接头的破坏试验研究;支座点与加载设备连接,将试验管片固定在加载设备上,为试验管片提供纵向力。
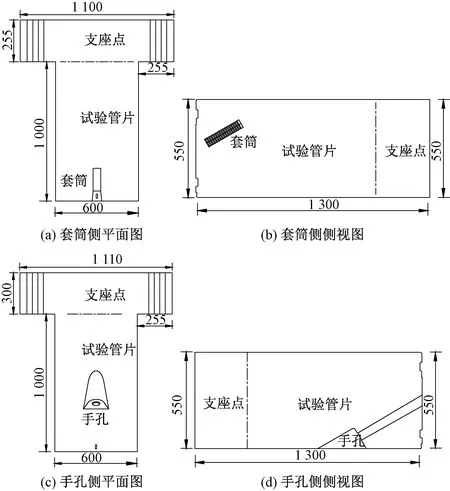
图13 试件尺寸(单位:mm)
试件在盾构隧道管片结构加载试验系统上进行加载,在纵向上试件与设备连接,为固定端。在环向,试件边界临空。
相关研究成果[1-3]显示受拉破坏为纵向接头的主要破坏形式。本研究采用足尺模型,在静力状态下为接头施加纵向拉力以至破坏。加载方式如下:为试验构件逐步施加纵向拉力荷载,直至构件破坏,记录构件破坏时的螺栓及混凝土应变极值。
加载初期,接头持续张开,螺栓应变增加,接头混凝土无明显变化。当纵向加载力接近323.2 kN时,裂纹从接缝面螺栓口处开始迅速扩展,接头位置发出致密而沉闷的破裂声,同时伴有混凝土碎屑掉落,构件发生破坏。此时螺栓应变为2 860.6×10-6,折合应力为600.6 MPa,未达到屈服强度(900 MPa)。
试验构件的破坏发生在套筒侧接缝面邻近外表面位置,即套筒受力外拔,带动邻近混凝土受拉,套筒周边最大主应力分布区逐步扩大,最终向邻近外表面的接缝面贯通,最终破坏形式以向外表面拓展的裂缝为主。试验构件手孔侧及套筒侧管片的接缝面螺栓孔位置均有裂缝出现,说明接头张开过程中螺栓对接缝面螺栓孔周边有挤压摩擦作用。
相对而言,手孔位置破坏较为轻微,在手孔两侧内表面上均有轻微裂纹。
除套筒侧外表面由于套筒受拉引起的裂缝扩展而有裂缝产生外,试验构件的内外表面均无裂缝出现,说明纵向接头在受力张开时,受力危险区主要位于管片内部,对表面影响有限。
记录构件破坏时管片混凝土应变,其内外表面靠近接缝处纵向应力分布见图14。

图14 破坏时接头混凝土纵向应变
由图14可知,构件破坏时接头混凝土纵向受力显著的表现出套筒侧外表面拉应变较大,手孔侧内表面压应变较大且以竖轴为对称轴呈对称分布的特点。
手孔侧外表面及套筒侧内表面应变较小,手孔侧内表面由于螺栓头挤压管片出现较大压应变分布区,压应变极值为130×10-6。而套筒侧外表面由于套筒受拉带动邻近混凝土变形出现较大的拉应变,拉应变极值为277×10-6。同时可见,试验中套筒受拉对邻近混凝土受力影响范围较小,拉应变分布区较窄,套筒侧外表面的边缘与中部受力不协调,使得外表面外侧出现部分压应变区。
5 结论
以实际工程为依托,基于子模型法研究了盾构隧道纵向接头在地震荷载作用下的受力变形特征,采用破坏试验的方式对其进行了验证,得到如下结论:
(1)对于盾构隧道纵向内力而言,当地震动沿隧道纵向激励时,以轴力和水平弯矩为主;当沿隧道横向激励时,以竖向弯矩为主。
(2)从数值结果来看,“纵向拉弯”及“纵向弯曲”两种工况下,接头受拉区的受力特征基本一致,均在手孔、接缝面及套筒周边出现最大主应力集中区,其中最大主应力极值出现在套筒周边。两种工况下管片表面纵向应力均为对称分布,但“纵向拉弯”工况下,张开量呈现非对称性,相对表面应力而言,接头变形对地震荷载更加敏感。
(3)受拉区的管片最大主应力、螺栓应力及接头张开量等,均显示地震荷载纵向激励时纵向接头受力变形更加危险,且纵向轴力对接头受力起主导作用。
(4)足尺试验中,接头破坏特征与数值结果基本一致,在套筒周边邻近外表面的接缝面区域出现较大破坏,手孔区域有轻微裂纹产生。内、外表面应变相对较小,手孔侧管片结构内表面出现较大压应变区,而套筒侧管片结构外表面出现较大拉应变区。
(5)接头破坏试验中,管片结构首先破坏,此时螺栓应力未达屈服强度。
