基于多端口网络理论及矩量法的电缆串扰研究

崔 勇，黄 鑫，杨晓凡

(北京交通大学 电子信息工程学院, 北京 100044)

电缆作为电子设备间最常用的一种信号传输通道，广泛应用于各个领域中。在某些应用场景，如铁路现场中电缆的铺设空间往往十分有限，线缆密度高，当电缆平行铺设时就会产生串扰问题，严重时会危害信号的正常传输甚至损坏设备。为保证电子设备的正常工作，对电缆间的串扰问题的研究十分必要。

现在常用的电缆串扰问题研究方法主要有以下几种：传输线法、时域有限差分法、有限元法、电磁拓扑法、矩量法等。文献[1-2]基于传输线法从时域和频域两方面对电缆串扰产生的原因以及影响做了研究。文献[3]结合时域有限差分法和传输线法对屏蔽电缆的电磁耦合问题进行了研究。文献[4]利用有限元方法，将研究区域划分为多个三角形，对非线性应控管改善畸变电场分布进行优化研究。文献[5]建立轨道电路电磁场模型，运用有限元法对其进行验证分析。文献[6-8]采用了电磁拓扑法分析了单导体传输线及屏蔽电缆的串扰问题。文献[9]运用矩量法研究了列车上电缆间的相互干扰问题。近年来运用各种电磁仿真软件对电缆串扰问题的研究也日渐增多，文献[10]和文献[11]分别运用了PSpice和CST来分析电缆间的串扰问题。

在实际的铁路现场中，电缆所处的电磁环境十分复杂，同一环境中往往含有多种类型的电缆，电缆的接地方式也多种多样。传统的传输线法在分析此种复杂问题时十分困难；单一有限时域差分法或矩量法等也存在计算量较大等问题；有限元法适用于复杂大系统且高频的情况，它在形成网格时计算成本很高；电磁拓扑法在分析复杂问题时较简单，但计算精度相对不高；而电磁仿真软件在分析一些含有较多影响因素的问题时建立的模型会十分复杂，需要花费相当多的时间在模型的建立上。

基于以上问题，本文介绍了一种运用多端口网络理论和矩量法相结合的串扰问题分析方法，适用于多条平行电缆、多层屏蔽层等复杂环境下电缆串扰问题的研究，同时具有相对较小的计算量以及相对较高的计算精度。该方法运用改进的多端口网络理论对多线传输系统进行了简化，并采用矩量法对多线传输系统的分布参数进行提取，同时采用对源点和场点进行多点划分的方式来对矩量法运算时遇到的奇异性问题进行处理，并引入虚拟节点理论将提取的分布参数转化为模型的传输函数矩阵。最后运用该方法仿真计算了不同情况下的线间串扰耦合系数。

1 多端口网络模型的建立

1.1 传统的多端口网络模型

假设在地面上平行分布有n根长为l的传输线，将其编号为1到n，每根传输线与地之间都构成回路，见图1。其中编号为1的传输线一端加干扰源，这里将干扰源等效为一个幅值为Vs的理想电压源和一个大小为Rs1的电阻串联的形式；另外一端接有大小为Rl1的接地负载，将这根线称为发射线。其余的线称为接收线，其中RsN和RlN(N=2,3…,n)分别为编号为N的接收线两端的接地负载。这里称靠近干扰源的一端为近端，远离干扰源的一端为远端。定义近端端口输入电流矩阵为I(0)，近端端口电压矩阵V(0)，近端负载矩阵为Rs；远端端口输出电流矩阵为I(l)，远端端口电压矩阵为V(l)，远端负载矩阵为Rl。

图1 多导体传输线系统示意图

根据图1可以得到端口电压矩阵和电流矩阵满足以下方程

( 1 )

同时，图1中虚线框中的部分可以简化为一个多端口网络模型，见图2。模型中共有2n个端口，端口电压矩阵和电流矩阵有以下关系

图2 多端口网络模型

( 2 )

端口导纳矩阵Y即为多端口网络模型的传输函数，其中：

(3)

式中：YPiPj为端口Pi和Pj之间的导纳，且有

YPiPj=YPjPi

( 4 )

结合式(1)和式(2)，可以得出多线传输系统的近端串扰系数Sn和远端串扰系数Sf满足下列的方程

( 5 )

( 6 )

1.2 改进的多端口网络模型

在实际情况中所使用的电缆往往有多层屏蔽层，见图3(a)，其中发射线为一根普通电缆，接收线为双层屏蔽电缆。这种情况可以等效为一个多线传输系统，其多端口网络模型见图3(b)，共有8个端口，则传输函数Y是一个为8×8的矩阵。

由于屏蔽层的屏蔽作用，发射线产生的电磁场对接收线芯线的直接影响非常小，干扰主要通过先耦合至接收线屏蔽层、屏蔽层上产生的干扰电压和电流再耦合到接收线芯线上的方式对传输的信号产生影响。由此可以对图3(b)的多端口网络模型进行分块处理，将一个大的模型等效为3个小模块的级联，见图4。其中Y1、Y2、Y3分别为发射线与接收线外屏蔽层、接收线外屏蔽层与内屏蔽层、内屏蔽层与芯线之间的传输函数，且都为4×4的矩阵。这样处理一方面减少了需要提取的端口间导纳的数量，降低了计算量；另外一方面可以根据不同模块的特性分别采用不同的分布参数提取方法，提高了计算精度，同时方便对不同接地方式以及同一系统中含有多种类型电缆时线间串扰问题的分析。

图3 双层屏蔽电缆传输系统及多端口模型示意图

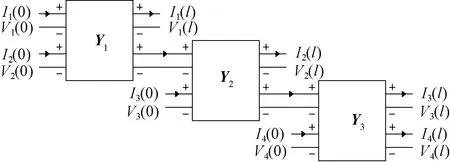
图4 改进多端口网络模型

2 算法介绍

2.1 基于矩量法的分布参数提取算法

矩量法是一种将线性算子方程离散化后，通过加权积分转换为矩阵方程进而求解的算法[12]。这里将电磁场混合积分方程[13]作为算子方程，运用矩量法提取多导体传输线系统的分布参数。

( 7 )

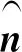
提取分布参数之前首先需要对导体进行网格划分，对于导体面采用三角形进行网格划分，每个三角形的中心作为一个节点。当导线的半径对系统的影响可以忽略时可将导线等效为一根线，此时采用线段对导线进行划分，取每一段线段的中心作为一个节点。

令入射电场为0，提取分布电感时，采用RWG基函数[12]对混合积分方程中的导体表面电流密度J(r′)进行离散。对于导体面采用的是二维RWG基函数，即将导体面划分为若干个三角形网格。对于导线采用的是一维RWG基函数，即将导线划分为若干个线段网格。根据RWG基函数的定义将相邻的两个网格分别标记为正和负，取每个网格中心为一个节点。运用伽辽金法[15]对离散后的混合积分方程进行扩展，转化为矩阵方程后计算可得到第m对网格在第n对网格处产生的节点分布电感Lmn为

( 8 )

Lsmn=μ(Msm+n+-Msm+n--Msm-n++Msm-n-)

( 9 )

式中：Lwmn为导体面上的节点分布电感；Lsmn为导线上的节点分布电感；m±和n±分别为第m对和第n对网格中的正负网格的节点，且有

(10)

(11)

式中：p和q代表网格节点, 即m±和n±；Ap为第p个节点所处三角形网格的面积；lp为第p个节点所处线段网格的长度。

jωLi-ΛΦ=0

(12)

式中：L为分布电感矩阵；i为节点电流矩阵；Ф为节点电位矩阵；Λ为将节点数量与网格的边缘数量联系起来的连接矩阵，其元素为

(13)

提取分布电容时，采用的是脉冲函数对导体表面电荷密度σ(r′)进行离散。同样应用伽辽金法对离散后的混合积分方程进行扩展，计算得导体面和导线的节点分布电容矩阵满足下列的分布电容方程

(14)

式中：Q为节点总电荷矩阵；C为分布电容矩阵，对于导体面和导线都有

(15)

其中，

(16)

(17)

另一方面，由电流连续性方程有第n个网格上的总电荷Q可以用流出该网格的电流表示，流出第n个网格的电流又可以表示为流过该网格的所有节点电流i与外加电流Ie的和。因此电流连续性方程可以改写为矩阵形式

(18)

结合式(12)、式(14)以及式(18)推导可得

(19)

进一步计算可以得到多导体传输系统的节点导纳矩阵为

(20)

2.2 算法奇异性处理

采用RWG基函数对导体表面电流密度进行扩展，当源点r′和场点r重合，即源点r′和场点r位于同一个网格上时，格林函数会产生奇异性[16-17]。为解决这一问题，采用近似等效的方法：将源点或场点进行多点划分，即将一个网格划分为x个大小相等的小网格，每个小网格的中心作为一个新的节点，用新节点的集合来代替原来的源点或场点，见图5。

图5 对场点采用4点划分示意图

划分后可以将Mpq和Wpq中的积分计算转化为累加计算，这里将源点和场点分别进行m和n点划分，则可以将Mpq和Wpq化为下列形式

(21)

(22)

2.3 基于虚拟节点理论的传输函数计算方法

为了将上文计算得到的节点导纳矩阵Yblock转换为多端口网络模型的端口导纳矩阵Y即传输函数，这里引入虚拟节点的概念[18]。假设RWG基函数对导体表面电流密度进行离散时将平行分布的n条传输线划分为了h段，即有h个真实节点，在每条传输线两端建立虚拟节点，则有2n个虚拟节点。真实节点间存在分布电容和分布电感，真实节点和地之间存在分布电容。由于虚拟节点没有实际的物理结构，因此虚拟节点不存在分布电容，仅和边缘的真实节点间存在半个分布电感。由虚拟节点和地之间组成多端口网络模型的端口，见图6。

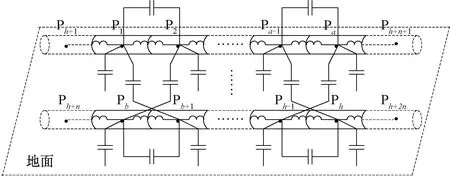
图6 引入虚拟节点的多端口网络节点示意图

则节点电压和节点电流的关系可用矩阵表示为

(23)

式(23)可简化为

(24)

式中：YD为虚拟节点间的导纳矩阵；YB和YC为虚拟节点和真实节点间的导纳矩阵；YA为真实节点间的导纳矩阵；Vport和Iport为端口的电压及电流矩阵；Vnode为真实节点的电压矩阵。由端口的电压和电流矩阵整理可得端口导纳矩阵Y，即多端口网络的传输函数为

(25)

3 仿真分析

3.1 不同高度及不同线间距仿真分析

利用上述的模型及算法，编写计算程序，仿真计算并测量发射电缆及接收电缆在距地不同高度，以及两者间不同间距的情况下的串扰耦合系数。设置的模型参数为：两根电缆型号都为LIFY_0qmm75，长为4 m，发射线和接收线处于同一水平面上，近端负载和远端负载都为50 Ω，根据上述模型参数运用本文介绍的方法仿真计算不同高度和不同线间距下两线间的近端串扰耦合系数，仿真的频率范围为1 kHz～2 MHz，将基于本文介绍方法的仿真结果与实际测试结果，以及基于电磁拓扑法的仿真结果进行对比，见图7。

图7 不同高度及不同间距仿真及实测结果对比

其中实际测试采用RIGOL DG1032型号的信号发生器来作为干扰源，采用RIGOL DS2102E型号示波器来采集接收线近端电压，计算得到实际近端串扰耦合系数，实际测试频率范围同样为1 kHz～2 MHz。

同时运用电磁拓扑法计算相同参数下的近端串扰耦合系数。对比本文方法的计算结果、电磁拓扑法的计算结果以及实际测试结果可以看出，本文方法的计算结果与实际测量值在主要频段上基本吻合，相比于电磁拓扑法的计算结果具有更高的精度。通过对比验证了本文介绍的模型及算法在分析不同高度及不同间距的电缆间串扰问题时都能具有较高的精确性。

3.2 不同接地方式仿真分析

对于屏蔽电缆不同接地方式下串扰耦合系数的仿真，首先以单层屏蔽电缆为例，计算了单层屏蔽电缆在屏蔽层浮地、单端接地及双端接地三种情况下的串扰耦合系数。其中接收线采用实际中常用的RG58型单层屏蔽同轴电缆。仿真计算两线间的近端串扰耦合系数，考虑实际铁路现场中铺设的电缆往往都比较长，同时电缆中传输的信号频率主要在1 MHz以下，这里设置发射线及接收线长度都为1 000 m，近端负载和远端负载都为50 Ω，屏蔽层直接接地，仿真范围为100 Hz～1 MHz。在电磁仿真软件CST中依照相同的参数搭建模型进行对比仿真，将基于本文介绍方法的仿真结果与CST的仿真结果进行对比，见图8。

图8 单层屏蔽电缆不同接地方式仿真结果对比

由图8可以看出,在1 kHz以下较低的频段屏蔽层是否接地对于电缆串扰耦合系数的影响不大；随着频率的增大，屏蔽层接地抑制了容性耦合，屏蔽层接地时的耦合系数低于屏蔽层不接地时的耦合系数；同时，可以看出屏蔽层单端接地的耦合系数与双端接地的耦合系数相差不大，而双端接地的耦合系数下降明显，这表明此时电缆间串扰以感性耦合为主，双端接地同时还抑制了感性耦合。当频率升高到使传输线相对于信号波长为电长传输线时[1]，本文介绍的串扰分析方法不再适用，因此结果不具有参考意义。

同时,本文介绍的方法的计算值和CST的仿真结果在屏蔽层不同接地方式时都具有较高的重合度，进一步验证了本文介绍的模型及算法在分析电缆串扰问题时具有较高的精确性。但是商业仿真软件CST的价格昂贵，同时在使用CST进行仿真时需要在软件中建立实际系统的等效模型，花费的时间要远大于本文介绍的方法。

接下来用本文介绍的方法对多层屏蔽电缆不同接地方式下的串扰进行分析。在实际铁路现场中使用的电缆往往含有多层屏蔽层，例如列车上使用的Profibus总线含有两层屏蔽层，这里以双层屏蔽电缆为例。由单层屏蔽电缆的分析可知当屏蔽层双端接地时电缆间的串扰耦合系数最小，因此这里令双层屏蔽电缆的外屏蔽层双端接地，并分析内屏蔽电缆单端接地与双端接地方式下的串扰情况。设置发射线及接收线长度都为1 000 m，近端负载和远端负载都为50 Ω，屏蔽层直接接地，仿真范围为100 Hz～1 MHz，仿真结果见图9。

图9 双层屏蔽电缆外屏蔽层双端接地，内屏蔽层不同接地方式仿真结果对比

由图9可以看出，对于多层屏蔽电缆串扰的仿真，本文介绍的方法与CST的仿真结果同样能达到非常高的吻合度。对于多层屏蔽电缆，在小于1 kHz较低的频段，接地方式对于电缆串扰的影响同样十分有限，在较高的频段，内屏蔽层双端接地时的耦合系数低于单端接地时的耦合系数，但差距并不大。

4 结论

本文介绍了一种多端口网络理论及矩量法相结合的电缆串扰问题分析方法。该方法运用多端口网络理论对多线传输系统进行建模，将多线传输系统进行简化，适用于对复杂问题的分析。该方法采用了基于矩量法的分布参数提取算法，同时运用虚拟节点理论来将分布参数转化为模型的传输函数，

对比结果显示本文介绍的分析方法对电缆间串扰的计算结果与实际测试值基本吻合。相比于电磁拓扑法，本文介绍方法的计算结果整体具有更高的精度。在对单层及双层屏蔽电缆不同接地方式下的串扰问题的分析中，本文介绍方法的计算结果和CST的仿真结果都能达到较好的重合度。

仿真结果表明，在1 kHz以下频率，屏蔽电缆的串扰受屏蔽层接地方式的影响很小；在1 kHz以上频率，电缆屏蔽层双端接地要比其他接地方式时的串扰小。但在实际的使用中，还需要根据具体情况确定屏蔽层的接地方式，例如ZPW-2000系列轨道电路的轨旁信号电缆，其屏蔽层的接地通过与贯通地线相连实现，如果内屏蔽层采用双端接地，可能会导致贯通地线中的部分牵引电流通过内屏蔽层回流而烧损电缆，因此在保证具有足够屏蔽效能的前提下，内屏蔽层应尽量采用单端接地方式。

由于本文介绍的方法在计算时忽略了屏蔽层厚度等因素的影响，同时在对算法奇异性处理时采用了近似等效的方法，因此计算值与实验室测试值以及CST的仿真值之间还存在着一定的误差。同时，本文的测试都是在实验室环境下进行的，缺乏计算值与现场环境实测值的比较。如何在建模时选取合适的等效模型将屏蔽层厚度等因素考虑进去、寻找更优的算法奇异性处理方法提高计算精度以及将此方法计算值与实际情况进行对比分析是下一步的研究重点。