基于卷积神经网络的防松铁丝断裂分类算法研究

王志学，张 渝，王 楠，罗 林

(西南交通大学 物理科学与技术学院，四川 成都 610031)

动车组异常检测技术对于保证动车运行安全具有重要意义。随着我国铁路运输行业的高速发展，运载量和运输里程大幅增加，如何通过检测动车关键部件来保障运行安全具有重要的现实意义。动车车体结构复杂，很多关键部件由大量螺栓连接固定，为防止螺栓丢失和松动，在螺栓上固定有防松铁丝。随着动车的长时间运行，由于振动、疲劳、锈蚀以及异物的撞击等原因，可能导致防松铁丝发生断裂，导致紧固螺栓发生松动或丢失。严重者，松动或丢失螺栓部位关键部件发生异常，威胁到动车的行车安全，甚至造成灾难性事故的发生。因此，及时发现螺栓防松铁丝异常，并进行修复，对保障动车行车安全具有重要意义。但是，传统的检测方法大部分为人工检测，检测效率较低，并且长时间检测会引起检测人员视觉疲劳，可能导致误检，人工检测不适合防松铁丝这种目标小、数量大的部件的检测。得益于工业相机的发展，使得对动车车体图像的采集变得更加容易，同时也促进了更多基于图像检测技术的发展。例如，在TEDS (Trouble of Moving EMU Detection System)系统中，将采集到的车体图像显示在计算机上，供检测人员进行在线检测，避免了外场检测环境的影响。但是，这种方法同样需要人工检测，并没有提升检测效率，降低检测成本。在防松铁丝检测中，采用的是先利用工业相机采集动车车底图片，再通过模板图像定位到铁丝部位，从而将铁丝图片裁剪下来供进一步检测的处理方式。针对采集得到的大量铁丝样本，研究一种高效、高准确性的针对螺栓防松铁丝断裂异常的智能检测算法具有较高的实际应用价值。

近年来，随着深度学习方法[1]的发展以及在图像处理领域所取得的瞩目成就，越来越多的计算机视觉方法均采用深度学习方法尤其是卷积神经网络。传统的特征提取方法，如SIFT[2-3]、SURF[4]和HOG[5]算法等，均采用人工设计特征，特征不丰富。而卷积神经网络具有强大的特征提取和非线性表达能力，可以提取更加丰富的特征，使得其在图像分类[6-7]、目标识别[8-10]、语义分割[11]等方面均取得了领先的水平。调研发现，目前有诸多学者结合铁路运输应用进行了一些这方面的研究。文献[12]提出一种级联Faster R-CNN目标识别网络，利用第一级别进行定位器支座部件的特征提取和定位，第二级别学习等电位线散股故障特征，再通过对比分析等电位线的正常及故障占比，实现等电位线的正常与故障分类，达到对等电位线不良状态检测的目的。文献[13]提出一种MCDDF (Multi-channel Defect Detection Framework)检测框架,先通过目标检测进行部件的定位，再将定位到的部件经过超分辨率提升后传入缺陷分类通道进行准确分类，结合两通道信息实现了缺陷检测任务。文献[14-15]将可变形卷积和在线困难样本挖掘引入到TEDS 缺陷检测与分割模型中，获得了较好的检测结果。为应对传统轨道检测方法由于对图像进行定位和分割会产生误差，从而干扰到后续分类精度的问题，文献[16]提出一种基于深度残差网络的轨道结构病害检测方法。此方法直接利用迁移学习方法和深度残差网络对不同的异常进行分类，获得了较好的识别准确率。文献[17]将Faster R-CNN应用到铁路异物侵限检测中，在对人、车以及部分动物的检测上达到了较好的精度。

上述检测方法针对的都是一些具有较明显异常的检测对象，而且检测对象在整幅图像中的面积占比较大。在防松铁丝断裂检测中，由于铁丝断裂处特征较少，特征区域较小(如图1所示，在c、d、e、f样本中，断裂处的特征不明显，而且由于特征区域小，在网络进行池化操作时，特征可能直接被池化掉，因此导致分类效果较差)，因此在利用传统图片分类方法，即采用单张图片直接进行分类时，分类精度不高，容易漏判误判，整体检测效果较差。

基于以上原因，本文提出一种基于并联卷积神经网络[18]的防松铁丝断裂分类模型，通过训练距离度量对防松铁丝进行分类。模型输入是防松铁丝图片对，一张是模板图片，另外一张是当前采集图片，通过比对两张图片的信息，判断铁丝是否断裂。与传统分类模型采用交叉熵作为损失函数不同的是，本模型采用距离度量来衡量图片之间的相似性，通过最小化无异常样本对的距离、最大化有异常样本对的距离达到分类的目的。为进一步提升模型的分类性能，引入一种双边界损失函数。

1 网络模型

1.1 分类模型

为实现基于距离度量的防松铁丝断裂分类算法，建立并联卷积神经网络模型。此模型由两个权值共享的CNN模型构成，两个模型分支分别接收两张图片(I1,I2)∈R1×H×W作为输入，通过一系列卷积、池化、激活操作，输出得到两组特征向量(fω,b(I1),fω,b(I2))∈Rc×h×w。这里I是输入图片，H和W代表图片的高和宽，1代表输入的是灰度图片，h和w代表特征向量的宽和高，c代表特征向量的维度，f代表从输入图片到特征空间的映射，ω和b为CNN的模型参数。为区分正负样本，令Ip和In分别表示正、负样本。模型通过计算特征向量fω,b(I1)和fω,b(I2)之间的距离作为图片I1和I2之间的相似性度量。对于具有断裂异常的正样本对，期望其相似性较小，或者距离更远；对于无异常的负样本对，期望图片对之间的相似性较大，或者距离更小。也就是说，模型训练的目的是增大类间距离，减小类内距离，从而达到样本划分的目的。

1.2 损失函数

基于以上优化目的，选取余弦距离和欧氏距离作为图片相似度的衡量。对于正负样本，尽可能增大类间距离，减小类内距离，使正负样本更加容易区分。

(1)余弦距离

基于余弦距离图片对特征向量之间的相似性可以表示为

( 1 )

对于正样本，由于断裂异常的存在，图片对之间差异较大，期望优化后的相似性越小越好。

( 2 )

对于负样本，图片对之间无异常，即认为具有更高的相似性，因此有

( 3 )

式中：i为训练中某一个样本对；m1和m2分别为优化的下边界和上边界。

因此损失函数Losscos可以设置为

( 4 )

式中：N为训练时每一个批次的大小；yi∈{0,1}代表样本对的标签，其中正样本yi=1，负样本yi=0。

式( 4 )表示的损失函数的意义是：

对于正样本，当其距离值大于m1时才对损失函数有贡献，当其距离值小于等于m1时，认为已经优化至既定的目标，不再优化，其对损失函数的贡献为0。

对于负样本，当其距离值小于m2时才对损失函数有贡献，若距离值大于等于m2，认为负样本已经优化至既定的目标，其对损失函数的贡献为0。

当m1=0和m2=1时，式( 4 )变为传统的对比损失函数。在传统对比损失函数中，直接优化正样本的距离趋近于1，优化负样本的距离趋近于0。理论上，只有完全相同的两张图片其相似性才为1。但是在实际样本中，由于铁丝的变形、部件的移动、光照和污渍等的影响，不存在完全相同的样本。因此，强制将余弦距离优化至趋于1是不合理的，同时也会增加模型训练的难度，对于负样本也是同样的道理。所以，双边界m1和m2的引入可以降低模型训练的难度，达到更好的分类性能。

(2)欧式距离

基于欧式距离的图片对特征向量之间的相似性可以表示为

Dl2(I1,I2)=‖fw,b(I1)-fw,b(I2)‖2

( 5 )

对于正样本，由于断裂异常的存在，优化图片对特征之间的欧氏距离至一个较大值，即

( 6 )

对于负样本，图片对之间无异常，距离较小，因此有

( 7 )

式中：i为某一个样本对；m1和m2为优化的下边界和上边界。

因此，基于欧氏距离的损失函数Lossl2可以表示为

( 8 )

2 实验结果与分析

2.1 数据集

实验所用的数据集全部来自利用工业相机采集到的动车组车底图像。具体做法是：先利用工业相机采集得到动车车底图像，再通过模板图像定位到所有待检测铁丝部位，通过裁剪得到防松铁丝样本。本数据集共包含2 617对样本，其中防松铁丝断裂样本(正样本)1 300对，无异常的样本(负样本)1 317对，所有图片均为灰度图。正样本中，除了铁丝断裂异常，还存在有一些水渍、污渍、光照等造成的伪异常，如图1中b样本、c样本所示。这类伪异常会带来较大的差异响应。对于负样本，强烈的光照变化、覆盖面较大的水渍、油渍，会导致较大的相似性变化，使得负样本具有较大的不相似性。为了获得更好的分类性能，模型需要对上述伪异常有较强的鲁棒性。

2.2 结果分析

在网络训练时，采用随机梯度下降算法进行优化。初始学习率设置为0.01，每30轮次衰减至之前的0.1。卷积神经网络的批大小为8，迭代轮次数为100轮。所有实验都是基于Pytorch 1.2.0深度学习框架编写，实验平台的GPU和CPU配置分别为Nvidia RTX2080Ti GPU和Intel i9-9900X CPU。对样本按照8∶1∶1划分为训练、验证、测试集，所有图片对都被调整为128×128大小输入网络。同时，图片送入网络前都会进行随机的水平、竖直翻转。网络模型均采用Resnet34模型[6]作为基本模型。模型每秒浮点运算次数为 3.7×1010FLOPs/s，推理速度为0.055 s/张。

在进行不同模型对比时，采用10折交叉验证的方法衡量模型性能，选取召回率(Recall)、准确率(Precision)和F1指数作为评价标准。为确保实验结果的准确性，且避免划分数据集对结果的影响，每次训练都随机生成训练集、验证集、测试集，所有结果均进行3次实验取平均值。

(1)不同损失函数的对比

为验证本文算法的有效性，将基于余弦距离和欧式距离的损失函数进行对比。同时，为验证双边界损失函数的有效性，针对单边界和双边界的设置也进行了对比。所有实验中m1和m2分别设置为0.1和0.7。值得注意的是，对于两种距离，余弦距离的值域是[0,1]，欧氏距离的值域范围是[0,+∞)。因此在设置损失函数时，为避免正样本的距离上界被优化至极大值，同时不利于模型收敛，基于欧氏距离的损失函数最少存在一个优化上界。因此，基于欧氏距离的对比实验中，并未包括双边界的实验项。实验结果见表1。

从表1可以看出，在防松铁丝断裂分类上，基于余弦距离的损失函数比基于欧式距离的损失函数获得了更好的分类性能。即使是未加入双边界的实验3也比基于欧氏距离中性能最好的实验2在F1指数上高出了7.5%。同时，不论对于余弦距离还是欧式距离，在F1评价指标上，加入双边界的对比损失函数较传统的未加双边界的对比损失函数提升明显(实验1、实验2的对比中，虽然实验2在召回率上比实验1降低了0.4%，但是在综合评价指标F1上提升了1.7%，整体性能实验2优于实验1)。例如，在基于余弦距离的对比损失函数中，实验6获得了最高的F1性能，比未加双边界的实验3提升了10.6%。为进行对比，实验4和实验5中仅仅加入了单边界，也较实验3获得了明显的提升，F1指数分别提升7.7%和2.2%。这也验证了本文双边界对比损失函数的有效性，即损失函数中优化边界的加入可以降低模型优化的难度，从而提升模型分类性能。

(2)超参数对模型性能的影响

在本文模型中，为提升分类模型的性能，提出一种双边界损失函数。为确定双边界损失函数中，两个超参数m1和m2对分类性能的影响，对不同的超参数值的组合进行了实验。采用余弦距离作为损失函数，m1作为优化的下界，取值分别为0、0.1、0.2、0.3、0.4，m2为优化的上界，取值为0.6、0.7、0.8、0.9、1.0。具体实验结果见表2。

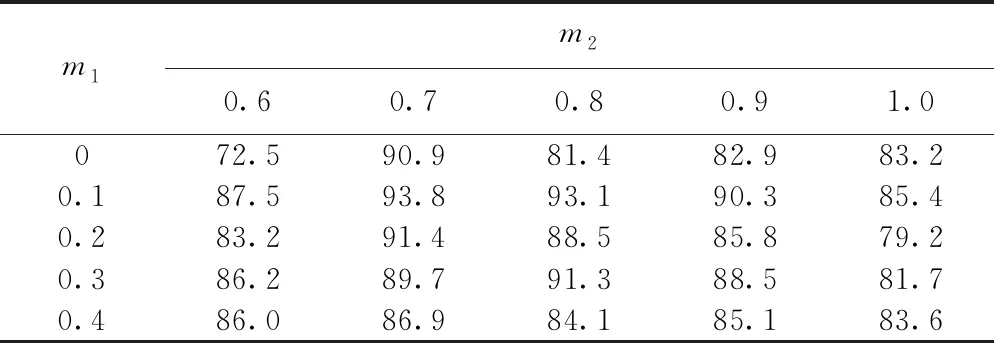
表2 不同双边界超参数的F1对比 %

由表2实验结果可以看到，当m1和m2分别为0.1和0.7时，模型在F1性能指标上达到最高为93.8%。为进一步讨论两个超参数对模型性能的影响，将表2中的数据分别以m1和m2为横轴绘制条形图。如图2(a)所示，观察其在同一m1值，不同m2值上的平均结果变化趋势，当m1=0.1时F1取得最高值，m1=0，F1最低。且在m1不为0的取值中，m1=0.4时的F1指数小于其他取值。由于m1是双边界损失函数的下界，可将其看作噪声容忍因子[19]，过小的值对噪声容忍度不高，缺乏鲁棒性，较高的值会降低模型对真实异常的响应度，降低模型性能。图2(b)中，观察其在同一m2值下，不同m1值上的平均结果变化趋势，当m2=0.7时，平均F1指数最高。

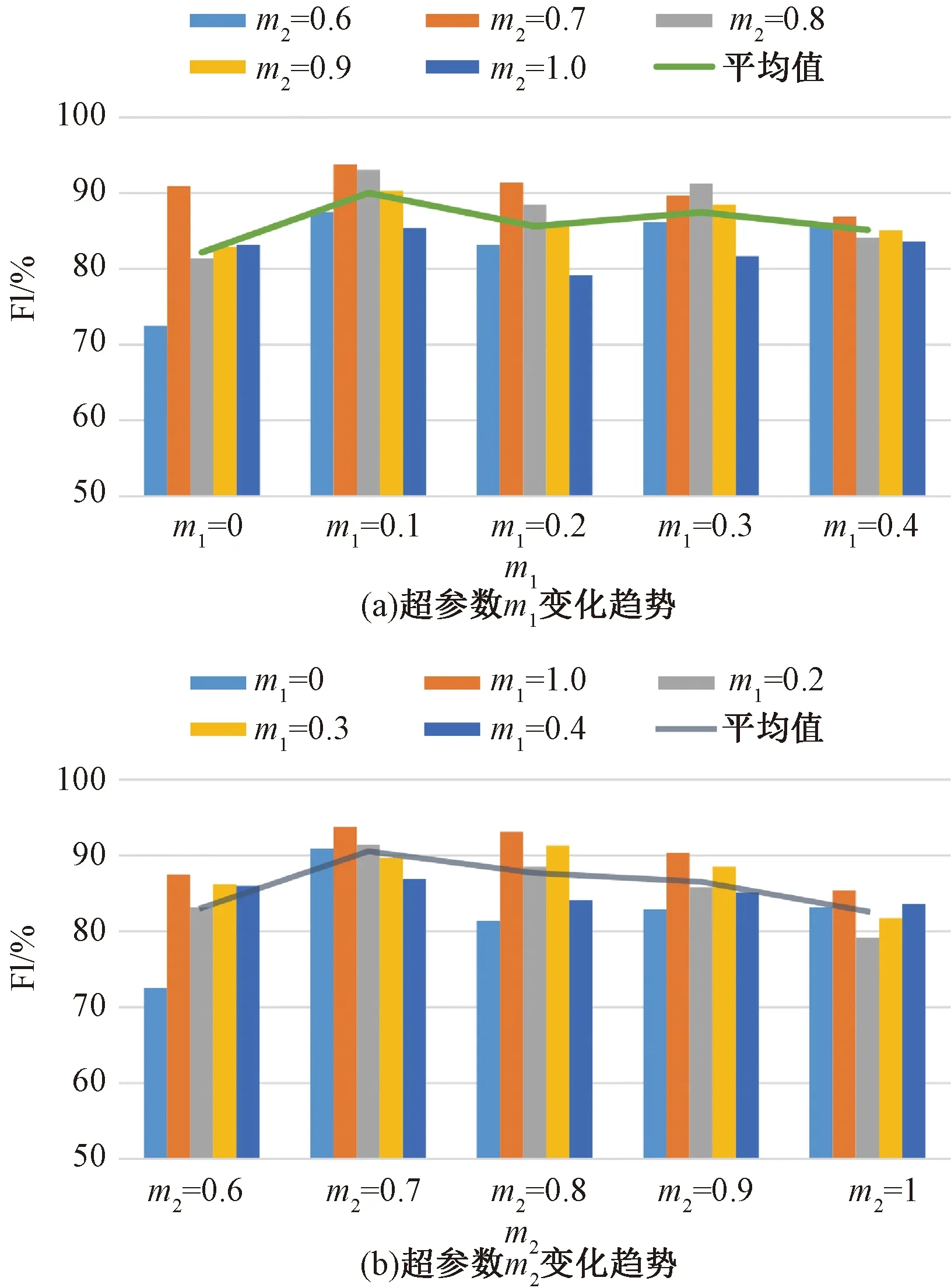
图2 不同超参数下的F1指数对比

(3)不同分类模型的对比

为与传统的分类方法(模型A)进行对比，建立3个常用的分类模型(模型B、C、D)，如图3所示。在模型B中，两张图片分别送入两个CNN分支进行特征提取，将两个分支的输出特征在通道维度进行合并。合并后的特征被送至全连接层和softmax层进行最后的分类。模型C采用经典的分类模型，即对铁丝图片进行二分类，正样本标签为1，负样本标签为0。与模型C不同的是，模型D直接将两张图片按通道维度组合成一张“二通道”图片送至网络进行分类。与模型B的不同在于，模型B中两个CNN分支分别提取两张图片的特征，再进行融合。而模型D直接将两张图片组成“二通道”图片送入网络进行特征提取，有助于模型从一开始就能提取图片对的融合信息，在综合考量两张图片信息的基础上进行分类判断。模型B、C、D均采用交叉熵损失函数进行训练。实验结果见表3。

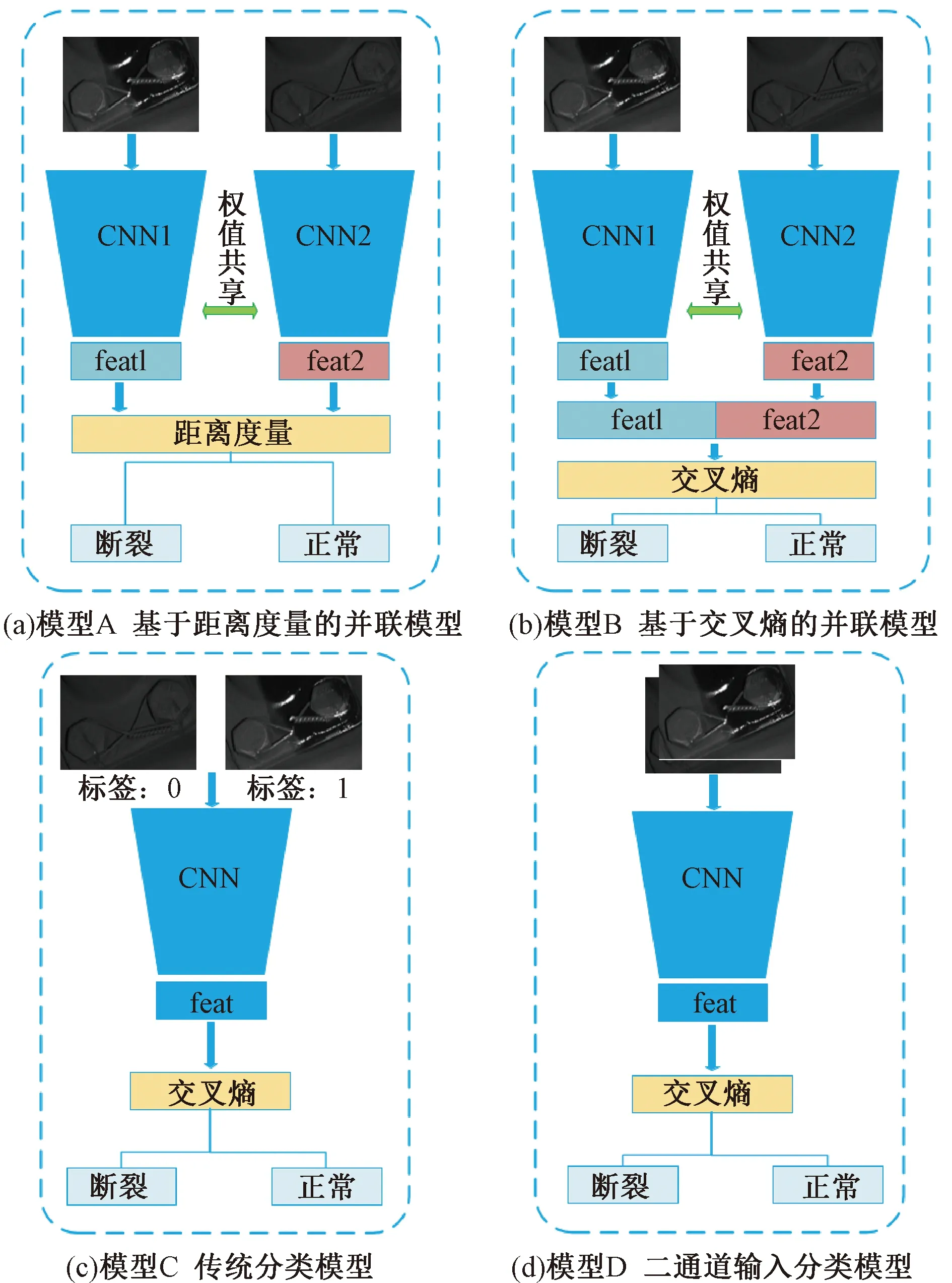
图3 防松铁丝断裂分类模型示意图

由表3实验结果可以看到，传统的基于交叉熵对图片进行分类的模型中，模型D比模型B获得了更好的结果。因为在模型D中，两张图片在输入网络之前被组合为一张“二通道”图片，更有利于提取两张图片的融合信息。即模型D提取的特征是建立在综合考量两张图片信息的基础上，因此获得了更好的性能提升。通过比较模型A和模型B、C、D可以看到，基于距离度量的模型在F1指数上有较大的提升，较模型B、C、D分别提升了13.5%、16.8%、8.2%。而且，在召回率和准确率上都达到了最高。因此，较基于交叉熵的分类模型，本文基于余弦距离度量图片相似性的模型可以获得更高的分类性能。

表3 不同分类模型的对比

3 鲁棒性验证

在基于距离度量的防松铁丝断裂分裂算法中，通过距离度量防松铁丝图片对之间的相似性，通过比较相似性或者图片一致性的大小，实现对防松铁丝图片的分类。但是，由于动车运行环境复杂，图片采集环境多变，防松铁丝图片中还有较多导致图片对差异较大的噪声。例如，图4正样本中b样本存在污渍；c样本存在大量油渍，而且因为油渍的存在，光照差异明显；d样本中由于补光的原因，图片对曝光不一致。同样，在图4负样本中，也存在大量水渍、油渍、光照等引起的伪异常。而且，从图4样本来看，由于部件的移动、转动、铁丝的变形等，每对图片之间还存在较大的结构性差异。

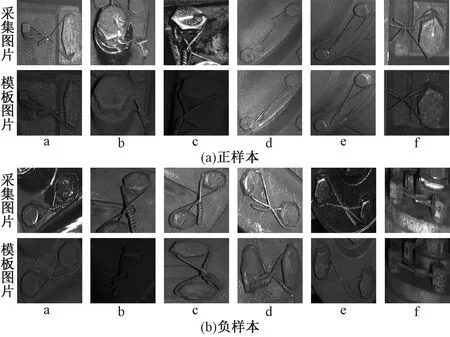
图4 鲁棒性测试样本对

由于铁丝断裂的特征信息较少，而噪声等伪异常和结构性差异的特征信息较多，导致图片对之间存在较大的不相似性。因此，算法能否应对噪声和结构性差异具有较强的鲁棒性，是对防松铁丝进行正确分类的关键之一。为验证本算法的鲁棒性，从正负样本中挑选了部分具有较大非异常差异的图片对进行测试，测试结果见表4。由于对比的样本是以一对图片作为基数计算其置信度，因此本对比实验未将模型C纳入测试。

表4 不同分类模型的鲁棒性对比 %

由表4测试结果可以看到，模型A中：对于正样本，b、c样本中存在油渍以及因为油渍带来的强烈光照变化，a、f 样本中存在曝光差异，但是模型分类为正样本的置信度达到90%以上。而且，从d、e样本可以看出，除了防松铁丝断裂区域，两对样本的噪声差异(如光照、油渍、水渍等)较少，但是模型还是以较高的置信度识别为正样本，说明模型对噪声有较高的鲁棒性。同样，对于负样本，a、b、e、f样本中分别存在油渍和光照、曝光不同、油渍、水渍的异常，图片对本身存在较大的差异性，相似性比较低。但是模型并没有因此类伪异常导致的大差异性将负样本误分为正样本。在c、d样本中，由于部件的转动，导致两次拍摄的图片形态不一致，图片对具有较大的结构不相似性，模型也能够对其进行正确的分类。

在与其他模型的对比中，可以看到模型B、C在一些大差异样本上的置信度较低，如模型B中，负样本a、e的置信度只有12.3%、42.8%，正样本d、e、f的置信度只有60%左右。模型C中，负样本a的置信度只有34.0%，正样本d、e、f的置信度为70%左右。若以50.0%作为阈值，模型B中的负样本a、e，模型C中的负样本a将被错分为正样本。同时，虽然模型B在正样本b、c的置信度达到了最高，对于其他样本，模型A均获得了最高的置信度。

由上述验证结果可知，本模型针对水渍、油渍、光照、曝光还有部件转动等导致的伪异常，较其他模型具有更强的鲁棒性。

4 结束语

在防松铁丝断裂分类任务中，由于断裂特征信息较少，特征区域小，不利于提取有效特征信息，从而导致传统分类方法精度不高。本文提出一种基于距离度量的孪生网络模型，通过距离衡量图片对之间的相似度，对图片进行正确分类。同时，相比传统的对比损失函数，本文提出的双边界对比损失函数，不仅降低了网络优化的难度，而且对噪声有较强的鲁棒性。实验结果表明，本文的分类模型较传统的分类模型性能更优，在准确率、召回率和F1指数上都高于传统分类模型。此外，模型对光照、污渍、曝光、部件移动和转动等伪差异具有较强的鲁棒性。