基于模糊自适应PID的定型机温度智能控制

苗荣霞,王 磊,杨 婧,刘鑫森

(西安工业大学,陕西 西安 710000)

织物在加工过程为了达到工艺要求,会承受各种形式的外力,进而导致织物内部结构发生变化。为了使织物内部结构重新恢复稳定,并使其质量获得改善和提高,需要对织物进行定型整理,定型机是对织物进行整理的设备。在定型过程中,需要在一定温度下对织物进行拉伸和拉幅,温度的精准控制是保证织物质量的关键因素,传统控制系统多采用PID控制器调节,但传统PID在系统运行开始后参数固定,无法应对温度大范围变化这类被控对象。研究基于模糊自适应PID控制算法在定型机温度控制系统中应用的可行性,使其实现对热风箱内温度的精准控制,满足织物定型的工艺要求。

1 定型机温度控制系统

温度控制系统是热定型过程中一个非常重要的组成部分,温度是否适宜直接决定定型织物的质量。热风箱通过对聚酯网的热处理来消除分子间内应力不均匀导致的织物形变,使纤维分子内部达到平衡状态。

定型机温度控制单元的作业过程包含两部分:一是必须快速无超调升温,包括起始升温和二次升温;二是在需要恒定温度时能够保持温度不发生变化。

图1为定型机的温度控制系统框图,操作人员通过上位机设置给定温度,现场热风箱内温度传感器采集环境温度,将模拟量信号转换为数字量信号上传给PLC,PLC使用环境温度与给定温度进行PID运算,再由数字量信号转换为模拟量信号控制电力调整器,由电力调整器控制输出电压,调节电加热管的输出,保证环境温度与给定温度一致。

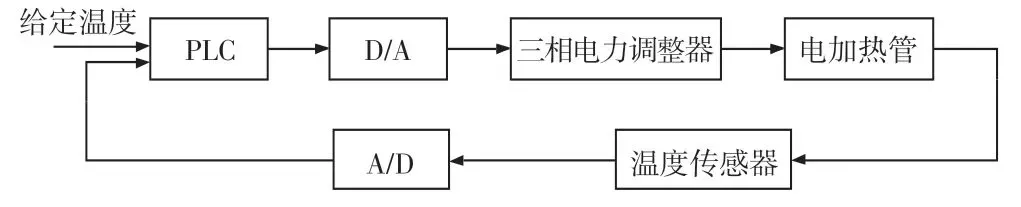
图1 温度控制示意图

2 温度系统数学模型

温度控制系统中采用空气对流式加热系统对织物表面进行加热,在热风箱中使用多个电加热管对热风箱内空气进行加热。被控对象的被控参数为热风箱内温度T,控制量为电热丝两端电压u,设加热丝质量为M,比热为C,热传系数为H,热传面积为A,未加温前热风箱内温度为T0,加热后温度为T。

根据热力学知识有:

式中,Qi为单位时间内电热丝产生的热量。

考虑到Qi与外加电压u的平方成比例,故Qi与u是非线性关系。对平衡点(Q0,u0)周围进行线性化处理,得:

于是可得微分增量方程:

考虑到控制系统存在迟滞性和鲁棒性,所以在公式(4)的基础上串联一个滞后环节,最终得到热风箱内温度变化量与给定电加热管的电压变化量之间的传递函数为:

由试验数据可算出K=1,T=3,τ=3。

3 模糊自适应PID控制

3.1 算法分析

定型机温度控制系统属于典型的负反馈系统,该系统由PLC、电加热管、温度传感器、三相电力调整器等设备构成。由于温控系统属于非线性控制系统,各参数不断变化,为了达到控制要求,必须对参数进行不断设置,传统PID控制系统往往没有准确的模型,导致参数难以确定。利用模糊控制规则调节PID参数,实现了对热风箱内温度的精准控制。

基于PLC的模糊自适应PID控制器设计,由操作员通过上位机输入温度给定值,记为rin,热风箱内温度采集平均值为系统输出,通过测量装置反馈给系统,也是系统反馈值,记为yout,PLC经过PID算法整定后输出模拟量信号电压值通过三相电力调整器控制电加热管,Kp、Ki、Kd分别为PID控制器的控制系数。模糊自适应PID控制器结构如图2所示。

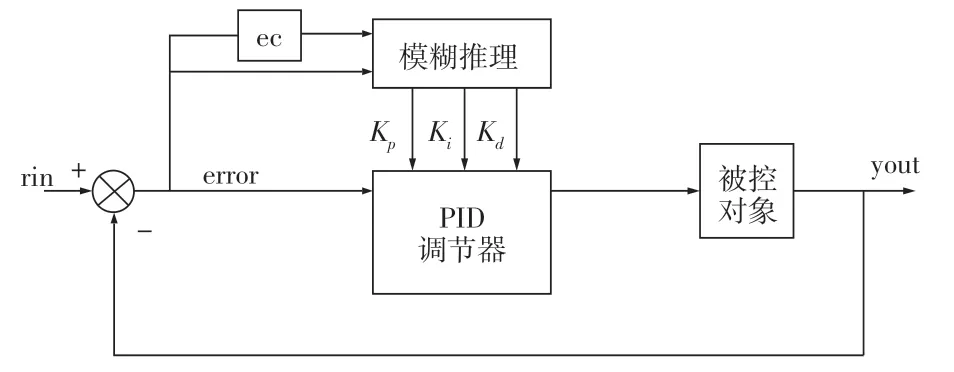
图2 模糊自适应PID控制器

3.2 算法实现

定型机温度模糊自适应PID控制器是一个二维控制器,输入变量为现场实际温度与操作员的设定温度之差e和误差的变化率ec,根据实际控制需求,对于误差e和误差变化率ec的模糊集定义为:

以工程项目中实际的误差变化范围以及误差变化率大小确定e和ec的基本论域为:

隶属度函数曲线如图3所示。

图3 隶属度函数曲线

参数的整定规则是模糊控制的核心部分。根据现场实际情况以及专家经验可以得到以下整定规则,表1为模糊控制规则表。

表1 模糊控制规则

表1中NB、NM、NS、ZO、PS、PM、PB分别表示负大、负中、负小、零、正小、正中、正大。采用最大隶属度法对输入信息进行模糊化处理,隶属度图形选取三角隶属函数,使用加权平均法将模糊量转化为论域中表示的清晰量,最终转化为所需实际控量。

在实际运行过程中,控制系统通过查询模糊控制规则表并进行进一步的运算,进而对PID参数完成校正,模糊PID控制器参数调整方式为:

将运算调整后的PID参数写入PLC系统的PID算法控制模块中,最终PLC用于控制三相电力调整器的模拟量电压输出信号值为:

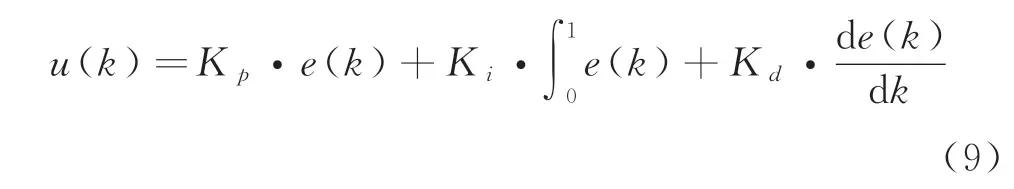
模糊PID控制流程如图4所示。

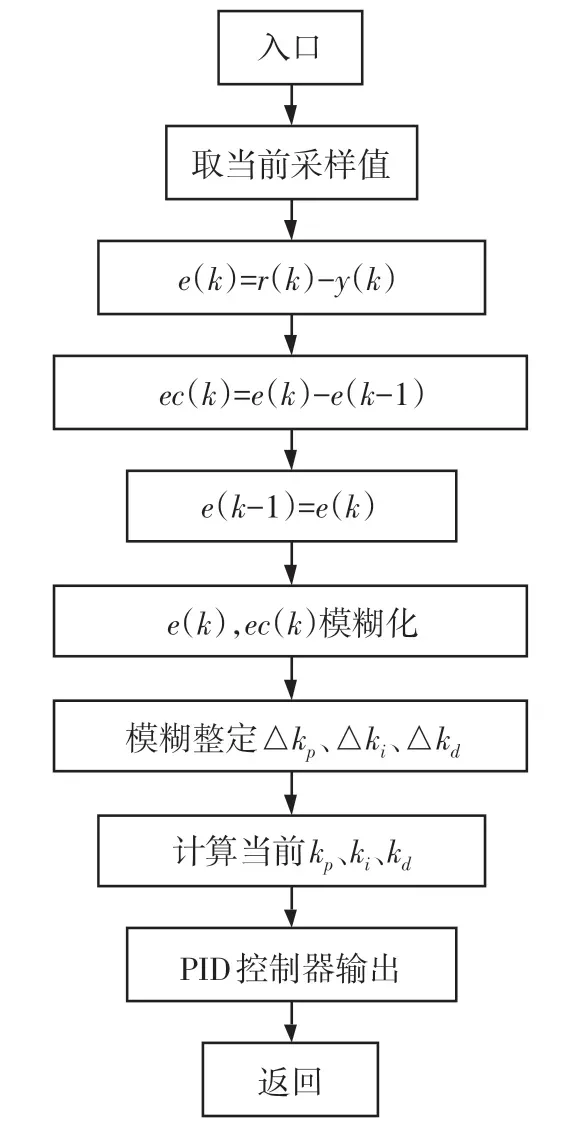
图4 模糊PID控制流程

在实际工作现场中,温度传感器采集现场环境温度,PLC接收温度传感器反馈的模拟量信号进行PID运算,PID参数需要实时调整在线修正,因此在PLC和上位机之间需要建立数据通道,作为PLC和上位机数据交换的服务器。本文用到基于OPC服务器,将底层PLC计算得到的误差e和误差变化率ec读取到上位机的MATLAB软件中,作为模糊控制器的输入,经过模糊推理和决策,得到PID控制器的3个参数调整值ΔKp、ΔKi、ΔKd,PLC接收来自上位机的PID参数,再结合初始参数进行运算得出实际控制参数。

4 仿真及结果分析

为了检验该系统控制算法能否有效控制热风箱内温度变化,对系统控制算法进行仿真试验。根据定型机温度控制系统的数学模型,该仿真模型在输入端输入阶跃信号,在不考虑其他信号干扰的情况下,利用传统PID控制器和模糊自适应控制器,分别对输入信号进行处理,观察输出端信号变化情况,如图5所示。

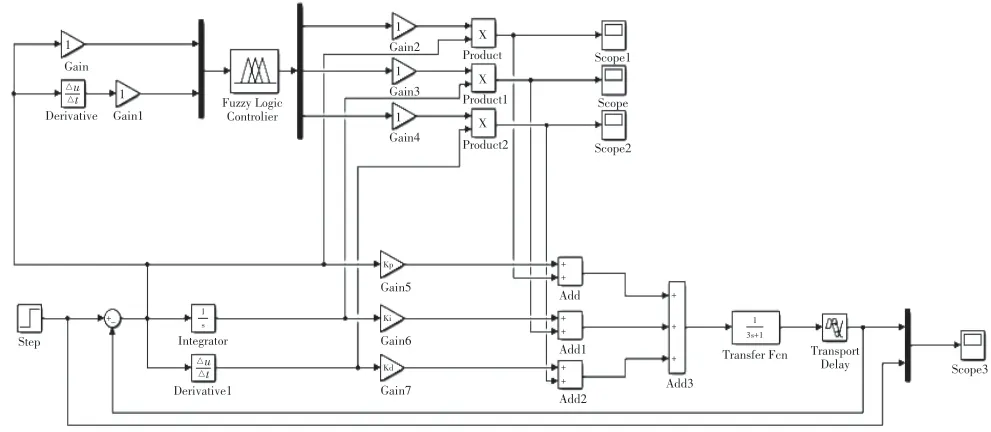
图5 系统模型搭建

当设定温度值为100℃时,模糊PID的温度输出曲线如图6所示,虚线是传统PID控制曲线,实线为模糊PID控制效果曲线,从图6中可以看出传统PID具有较大的超调量,并且响应时间较长,与传统PID控制器相比,模糊自适应PID控制响应速度快且几乎无超调,达到稳定之后稳态误差维持在±3%的范围内,满足控制系统的要求,进一步证实将模糊PID应用于热定型中温度控制的可行性与有效性。

图6 模糊自适应PID与PID控制响应曲线

5 结束语

研究基于PLC的定型机温度控制系统,该控制系统主要使用PLC做主控制器,对定型机的温度控制模块进行实时监测与控制,将模糊自适应PID控制算法应用于定型机温度控制系统中,通过在Matlab/simulink中搭建传统PID和模糊自适应PID模型进行仿真验证,证明模糊自适应算法使系统具有更好的动态性能和调节性能,能有效提高定型机温度控制系统的控制精度和控制效果,具有一定的工程应用价值。