基于PCA-BPNN的温室番茄果实直径预测模型

韩坤林，王钊英，杨会民，陈毅飞，蒋永新，张佳喜

(1.新疆农业大学机电工程学院，乌鲁木齐 830052；2.新疆农业科学院，乌鲁木齐 8300091；3.新疆农业科学院农业机械化研究所，乌鲁木齐 830091)

0 引 言

【研究意义】高效利用水肥资源和建立合理的灌溉策略具有重要意义[1-3]。番茄果实生长状况在一定程度上反映了水肥盈缺情况，果实大小反映着其内部营养成分，也是和产量获取的重要因素，对果实直径进行预测有研究意义[4-6]。生长环境对果实发育大小有重要影响，良好光照条件和合适温度更有利于果实生长[7]。在对作物水肥决策时，果实大小是重要指标，而目前对果实大小的实时监测较为困难，对于数量多的作物，其中少数作物生长状态不能代表大多数作物，而通过环境信息和土壤信息进行预测的作物生长指标，可反映大多数作物的生长状态。果实生长实时生长状态一定程度上反映了水肥的盈缺情况，可根据果实实际生长情况与预测情况的差值对水肥进行调节[8]。【前人研究进展】程智慧等[9]根据7个环境因子对番茄果实生长发育产生的影响，采用逐步回归分析法建立了3个品种番茄果实增量与显著环境变量的回归模型，并提出了3个番茄品质分别适合生长的环境因子范围，以及果实增量达到最大时的环境因子组合。李慧霞等[10]对番茄生长补光和增施二氧化碳，该方法对番茄的各个生长指标的影响，补光和增施二氧化碳对番茄果实横纵径等有较大影响。胡笑涛等[11]研究了果实直径在不同天气以及不同土壤含水率的变化规律，结果表明，果实直径变化与太阳辐射强度有紧密联系，而与土壤含水率的关系不太密切。Heuvelink[12]把番茄果实生长与日平均温度结合在一起，果实生长还与光照强度有很大关系[13-14]。【本研究切入点】目前基于温室环境信息和番茄自身生理生态信息结合的预测果实生长的研究较少，且手段单一繁杂，实用性低，不能真正实时结合环境因子以及作物自身信息进行预测。作物实际生长变化情况与实时空气温度、土壤含水率、空气湿度等因素关系密切，需要不断采集实时环境信息进行判断作物对灌溉量和施肥量的需求。【拟解决的关键问题】以番茄果实横径为研究对象，将果实生长期内空气温度、空气湿度、果实横径以及土壤含水率作为研究数据，采用主成分分析法对数据进行分析，对提取的主成分和输出变量进行BP神经网络训练，建立PCA-BPNN模型。

1 材料与方法

1.1 材 料

番茄种植试验于2019年11月4日～2020年2月27日在新疆农业科学院农业机械化研究所连栋温室内温室进行，共种植56株生长期相同的盆栽番茄，抽取8株生长状态相似的果实膨大期番茄样本，其中5株进行训练，3株作为测试。番茄品种为天粉1号，所用花盆容量为10 L，底直径0.35 m，高0.3 m，栽培方式采用基质栽培，用草炭、蛭石和珍珠岩按3∶3∶1的比例混合而成作为基质，有机质58.62%、速效氮638.39 mg/kg、速效磷371.3 mg/kg、速效钾6 640 mg/kg作为初始基质含肥量。

利用物理生理生态数据采集系统，每隔30 min连续自动采集环境数据与番茄生理数据，在温室中主要考虑空气温度、空气湿度、叶片温度、果实直径变化、浅层土壤含水率和深层土壤含水率对番茄的影响建立预测模型，定期对传感器的安装检查调整，仪器精度能准确测得各数据，所得数据是真实有效的。表1

表1 植物生理生态数据采集系统性能指标Table 1 The Performance index of Plant physiological an ecological data collection system

选取番茄结果期数据的果实直径变化量作为预测指标。在安装果实大小传感器时，选取需要测量果实横径的番茄，将夹爪分开，使传感器能够将番茄果实保持在所需的位置，然后检查传感器是否牢固地压住果实，轻轻用力压紧夹爪，使其不易滑落，将传感器的电缆固定在阀杆上，防止传感器偶尔移动，并定期检查传感器的位置。图1

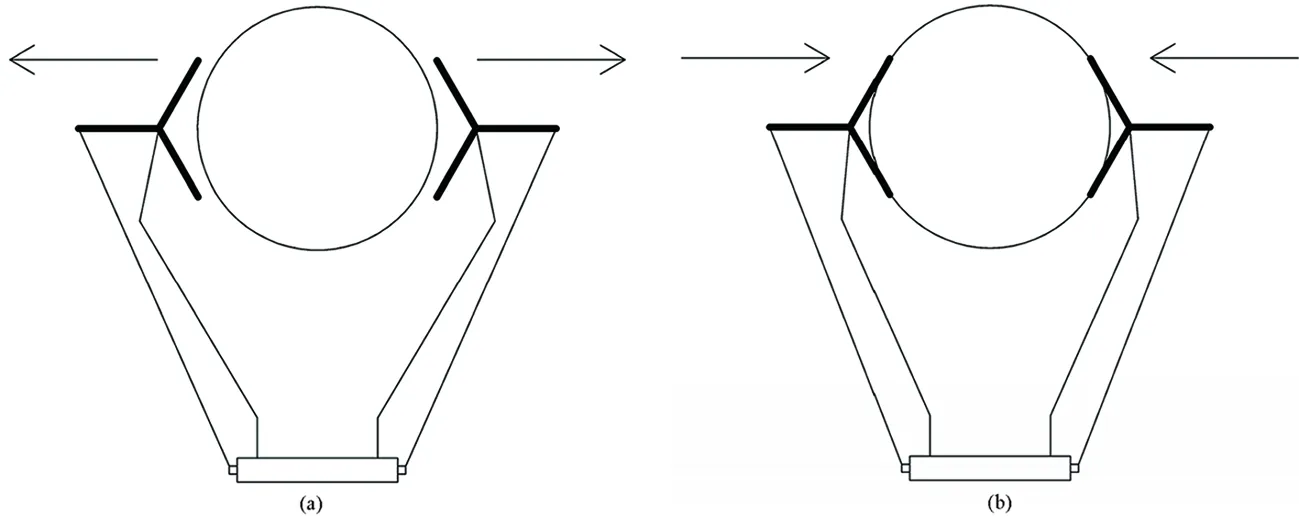
图1 果实直径传感器安装示意Fig.1 Schematic Diagram of Fruit Diameter Sensor Installation

在番茄的生长期内共采集了72 800条数据，此处选取了18 000条数据进行主成分分析和模型建立，并以3株番茄分别选取的连续30 h左右的360条数据进行模型验证。图2

图2 番茄试验布置Fig.2 Arrangement of tomato experiment

1.2 方 法

1.2.1 主成分

研究多维数据时只需要考虑少数的几个主成分，更容易获取主要的信息，提高数据分析效率[15-17]。使用MATLAB软件对数据进行主成分分析。

(1)确定输入输出

确定输入为5个变量，输出为1个变量，每个变量3 000条数据。输入变量依次为空气温度T、相对湿度RH、浅层土壤含水率V1、深层土壤含水率V2、叶片温度LT，输出变量为番茄果实横径D。

(2)数据标准化

对数据进行标准化，假设原数据构成n×p维矩阵X:

(1)

将X矩阵标准化为Z矩阵，其中

(2)

(3)求解相关系数矩阵特征值与特征向量

得到标准化矩阵Z，求ZT的相关系数矩阵R。

(3)

求解计算相关系数矩阵R的特征值λi和特征向量ai，其中λi值越大，方差贡献率就越大，所反映的主成分信息就越多[19]。MATLAB中求特征值与特征向量函数为eig。

(4)确定贡献率及建立主成分表达式

根据特征值λi确定主成分个数，第m个主成分贡献率为

(4)

累计贡献率如果已经能够反映大部分信息，可以将前m个因子作为主成分[20-21]。把前m个的主成分特征值λi所对应的特征向量ai为主成分表达式中的回归系数，主成分表达式由此可建立。

Fm=a1mZ1+a2kZ2+…+apkZp.

(5)

1.2.2 建立BPNN模型

(1) 数据预处理

对数据进行归一化，可以消除量纲互相之间的影响，可以提高求解精度以及训练速度[22]。研究中需要把输入、输出数据进行归一化在[0,1]区间，在MATLAB中归一化函数为mapminmax，归一化公式如式(6)[23]

(6)

(2) 确定BP神经网络拓扑结构

在输入输出数据都确定之后，可根据输入输出数据的节点个数和要求的训练精度确定隐含层层数与隐含层神经元个数[24-25]，在此处确定输入节点个数为3个，输出节点个数为1个，隐含层数为3，隐含层节点个数分别为12、6、6。

(3)训练BP神经网络及数据反归一化

确定神经网络拓扑结构后，进行训练神经网络[26-29]，中间传输层函数确定为“tansig”,隐含层至输出层传递函数为“purelin”，训练网络函数为“trainbr”，建立网络函数为newff,再结合数据对其进行仿真，仿真函数为sim。训练网络输出的结果需要进行反归一化，才能得到实际的果实变化预测量。

1.2.3 模型验证

把3株番茄的数据作为测试数据进行主成分分析后，提取前3个主成分并对其归一化再代入模型中，将输出结果归一化后也代入模型中，把仿真结果进行反归一化后可得到预测结果，其中决定系数R2和均方根误差RMSE可以很好地反映预测精度。公式如(7)[15]和(8)[30]：

(7)

(8)

2 结果与分析

2.1 模型建立

研究表明，前3个主成分的累积贡献率已经达到了93.47%，整体的大部分信息已经能够由前3个主成分反映，取m=3。提取前3个主成分向量进行载荷分析。对第1个主成分影响最大的是空气温度、相对湿度和叶片温度，1主成分F1基本包含了这3个指标的信息；对第2个主成分来说，影响最大的就是深层和浅层的土壤含水率；对第3个主成分影响最大的也是深层和浅层的土壤含水率；这3个主成分基本能反映这5个因素的指标信息。表2，表3

表2 初始因子载荷矩阵Table 2 Initial component matrix

在得到主成分表达式之后,确定BP神经网络的输入变量为F1、F2、F3，输出变量为果实直径变量，进行网络训练。

F1=0.584x1-0.530 1x2+0.261 1x3+0.060 4x4+0.553 3x5.

(9)

F2=0.126 8x1+0.071 3x2+0.626 2x3+0.745 8x4-0.174 7x5.

(10)

F3=0.146 1x1-0.139 2x2+0.694 1x3-0.649 5x4-0.235 9x5.

(11)

2.2 模型验证

研究表明，基于PCA-BPNN模型训练的第1株番茄的决定系数R2值为0.964，RMSE值为0.238，第2株番茄的决定系数R2值为0.960，RMSE值为0.051，第3株番茄的决定系数R2值为0.951，RMSE值为0.047，模型有较好的预测效果。图3，表4

表3 主成分提取Table 3 Principal component extraction and analysis

图3 样本1、2和3短期果实直径预测量和实测量比较Fig.3 Comparison between the predicted and measured values of samples 1，2and 3

3 讨 论

影响果实大小变化的主要因素有气温、土壤含水率以及植物自然生长发育等方面，研究选取了番茄果实膨大期时的果实横径变化数据，结合空气温度、相对湿度、土壤含水率，叶片温度等因素建立了以果实直径变化为因变量的PCA-BPNN模型，该模型参考了前人研究成果以及进行了网络的多次训练[24]，确定了最终的主要参数，并结合主成分分析法和神经网络，提高了模型的精度，能够进行有效的预测。

员玉良等[16]以向日葵和番茄为对象，对其茎秆变化进行了研究，预测值与实测值相关分析的决定系数为0.649～0.782。陈毅飞[31]等采用多层感知机训练方法，研究了番茄茎秆动态预测方法，预测值与实测值的回归系数为0.901，具有较好的效果。程智慧[9]等通过空气温度和空气湿度等多种因子的变化建立了与果实增量的关系，不同环境因素对番茄果实生长的影响。对果实生长变化具有一定的局限性，该模型的建立依赖于固定水肥条件下所测得的参数以及新疆独特的地理气候条件，而番茄生长发育情况与气候、地域和水肥也有很大关系，可以在原有的水肥配方上设置不同的水肥处理水平，最后根据长势最好的一组番茄数据进行模型建立，可以使番茄处于一个更好水肥环境。更准确地预测番茄所需的水肥量，还需要将果实生长变化、多种环境因子、作物自身其他生长发育情况以及农艺等因素综合考虑。

表4 样本1、2和3的预测值与实测值样本对比Table 4 Comparison between the predicted and measured values of samples 1，2 and 3

4 结 论

将环境因子数据和植物本体数据与主成分分析法和BPNN算法融合一起，建立了一种能在短时间预测果实直径变化的模型，并用3株番茄数据对该模型进行了测试和对模型性能进行了分析。建立的预测模型取得了良好的预测结果，误差最大值为0.075 mm，该模型在秋季番茄果实膨大期内能够较好预测番茄果实生长趋势，可用于新疆连栋温室内番茄果实横径变化量的预测。