随机扰动优化和多模型融合的目标密度非线性重建

许金鑫，李庆武，管志强，王肖霖

（1 南京船舶雷达研究所，南京211106）

（2 河海大学物联网工程学院，江苏常州213002）

0 引言

作为研究武器内部结构的重要手段，高能闪光X 射线照相技术可以获得目标内爆和演化过程的清晰图像。高能闪光X 射线照相中目标的密度重建属于典型的高维非线性反演问题，密度重建过程会遇到一些难题，包括数据维度高、投影图像中存在噪声和模糊等，影响图像重建的质量［1-3］。

由于需要有效地提供重建结果的不确定度以更好地量化武器的内部信息，基于统计的马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，MCMC）算法逐渐得到了研究，MCMC［4-5］作为一类重要的随机采样算法，能对后验分布提供全面的描述。目前高维数据下MCMC 重建算法的研究主要集中在线性模型上，非线性重建方面的研究较少。由于忽略了系统模糊对重建结果的影响，线性重建结果在目标界面区域易受模糊的影响。因此需在更符合实际成像过程的非线性模型上构建贝叶斯重建模型，对后验分布进行有效采样并提供相应的不确定度分析。高能闪光X 射线投影数据维度较高，相比于线性模型非线性成像模型涉及系统模糊的计算且无法像线性模型一样推导出目标参数的均值和方差形式从而直接采样，直接对非线性成像模型进行MCMC 求解存在计算量大以及推理复杂等问题。

文献［6］研究了一种先随机后优化（Random Then Optimizion，RTO）的非线性重建算法，通过求解振荡的优化问题对近似的后验分布进行采样。进一步，文献［7］在RTO 算法的基础上构造非线性分层贝叶斯模型，避免了正则项参数的人为选取。文献［8］将RTO 算法扩展到非高斯先验，通过变量变换建立非高斯先验与高斯先验模型间的联系。针对RTO 算法在处理高维数据时存在计算量大的问题，文献［9］引入一种新的子空间加速策略使得RTO 算法的计算复杂度与目标参数的维度成线性比例关系。在此基础上，文献［10］将RTO 和伪边际MCMC 结合以提高对模型参数鲁棒的采样性能。此外，随机最大后验（Random Maximum Posterior，rMAP）算法［11］避免了随机最大似然（Randomized Maximum Likelihood，RML）［12-13］算法需要评估正向模型二阶导数带来的昂贵计算。

RTO 算法及其改进方案更多地为了提高样本统计效率或计算效率，在降低样本统计误差方面的研究较少。多级技术［14-16］和多保真度技术［17-18］通过分析优化问题从而实现给定替代模型集的最佳分配利用。文献［17］研究了一种模型管理策略，在误差和成本方面平衡了高保真和替代模型的模型评估数量，从而加速估计具有昂贵计算成本的高保真度模型的样本统计量。该算法中优化的目标函数建立在多个替代模型的样本统计差之上，最终得到的样本融合统计量相比于单一的高保真度模型估计的统计量在精度上的提升并不明显。

基于上述讨论，本文结合实际估计的模糊核，提出一种基于随机扰动优化和多模型融合的高能闪光X射线图像非线性重建算法。首先，在非线性正向模型下构建分层贝叶斯模型，采用弱信息先验定义与噪声和先验精度参数有关的超参数以获得相对于共轭先验更合理的重建结果。然后，基于随机扰动的RTO 算法研究一种适用于高维数据的求解模型，结合雅可比矩阵投影约束该优化模型的求解，并设计相应的提议分布在M-H 框架中进行样本的接受判别计算，以降低样本统计偏差。最后，研究一种新颖的多模型融合方案，有效提高非线性模型样本估计的效率和目标高密度、边界区域重建的准确度。

1 加速随机扰动的非线性分层MCMC 重建

1.1 非线性重建模型及其最小二乘解

1.2 基于弱信息超先验的分层贝叶斯模型

1.3 加速随机扰动优化求解

式中，|Jx|涉及协方差矩阵的求逆以及一阶导数间相乘，高维度模型下的计算仍复杂。由于正向投影过程是对线吸收系数矩阵的每一行依次扫描产生投影数据，线性模型下相邻行之间相互独立。受模糊核的影响，非线性模型下投影图像中任意一行数据受线吸收系数矩阵中当前行数据以及以模糊核半径覆盖范围内的上、下行数据的影响，此时∇f(x)T∇f(x)为对称矩阵且数值集中在对角线附近区域，如图1所示。较亮区域数值非零且以块状依次分布在对角线上，称为“有效矩阵块”。假设线吸收系数矩阵的行、列数均为M，模糊核大小k×k，则图1（a）中任意一个有效矩阵块的大小为(M/2)×(M/2)（红圈区域），非线性模型中任意一行线吸收系数则对应((2k-1)M/2) ×((2k-1)M/2)大小的有效矩阵（红色正方形区域，红圈区域为中心有效矩阵块）。因此，可通过任意一行线吸收系数对应的有效矩阵来替代完整的一阶导数乘积近似计算|Jx|，精度矩阵的行、列数也由原先的(M/2)×M降至(M/2)×(2k-1)，有效减少高维数据下接受率的计算量。

图1 不同正向模型的一阶导数乘积Fig.1 First derivative products of different forward models

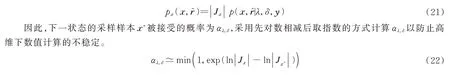
2 最小方差约束的多模型蒙特卡罗估计

2.1 最小方差约束的融合模型

2.2 融合模型最优系数管理

3 实验结果与分析

为验证本文非线性重建算法的有效性，在常密度、变密度法国实验客体（French Test Object，FTO）透射率图像［22］上进行实验。以相对误差（Relative Error，RE）［4］、峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）和结构相似度（Structural Similarity Index Measurement，SSIM）［23］作为客观评价指标来分析算法的重建精度。样本统计效率通过积分自相关时间（Integral Autocorrelation Time，IACT）［6］来评估，IACT 通过马尔科夫链的自相关函数（Autocorrelation Function，ACF）［6］计算得到，表示获得一个独立样本所需的MCMC 步骤数量。

3.1 提议分布以及雅可比矩阵投影分析

为验证提议分布和雅可比矩阵投影约束共同作用下样本估计的可靠性，本小节在常密度FTO 图像上计算样本估计的精度和统计效率，并将RTO-MH 算法［6］得到的样本估计作为参考。在高维数据下不同的初始值x0会影响LM 算法的收敛速度以及重建结果的准确度，因此通过实验分析初始值设置对重建性能的影响。定义本文算法在采样过程中不考虑样本的接受判别，即统计所有采样样本的算法为RML，对分辨率为100×100 的常密度FTO 透射率图像进行非线性重建。图2 给出了三种设置下超参数λ、δ和目标参数的ACF 及IACT 值，横、纵坐标分别表示滞后时间和自相关系数，其中第一行数据对应非线性模型下的线性解，即模糊矩阵B为单位矩阵，每次采样中目标参数的初始值均为0.01。第二行中模糊矩阵B仍为单位矩阵，但当前采样下LM 算法的初始值为上一次采样得到的样本值。第三行数据则在非线性解下得到，B为标准模糊矩阵，目标参数的初始值均为0.01。可以看出，在高维数据下，本章算法依旧取得了与RTO-MH 算法相近的样本计算效率，且优于RML 算法。RML 算法由于缺少了样本的接受判别过程对不稳定的样本值也进行了统计导致样本统计效率较低。与RTO-MH 和RML 算法相比，本章算法可得到更低的IACT 值，拥有更高的统计效率。受目标参数维度较高的影响，相比于噪声精度参数，先验精度参数的采样样本具有更高的相关性。此外，从图2 中第三行与前两行结果对比可知，实际求解模型的准确性也会影响目标参数特别是超参数的统计效率。

图2 各算法样本估计的ACF 和IACTFig.2 ACF and IACT of sample estimation for each algorithm

图3 为各算法样本估计的RE 值和单次采样时间。从图3（a）可以看出，图2 中第三行所代表的非线性求解比第一、二行代表的线性求解更加准确，说明所构建模型准确的重要性。从图3（b）单次样本计算时间中可以看出，相比于线性求解，非线性求解需要更多的计算量以及内存需求，高效的线性求解也推动了本文多模型融合算法的研究与实施。从图3（b）中同一颜色的柱状图可以看出，本文算法由于简化了随机扰动的目标函数并对接受率的计算进行优化，在计算效率上相比于RTO-MH 算法得到较明显的提升，且与RML 算法相近。对比图3 中灰、绿色柱状图可知，对于RTO-MH 和RML 算法，虽然上一次采样的样本估计值作为当前采样中LM 算法初始值的设置可以得到相比于参数初始值为0.01 更准确的重建结果，但需要更多的计算时间。因此，本文LM 算法中目标参数初始值设置为x0=0.01，适用于随机扰动优化模型的求解，提议分布和雅可比矩阵投影约束也适用于FTO 透射率图像的非线性重建。

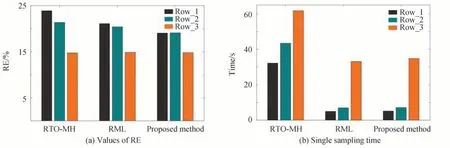
图3 各算法样本估计的RE 值和重建时间Fig.3 The RE of sample estimation and reconstructed time by each algorithm

3.2 多模型融合性能分析

定义模糊核1 和模糊核2，其中模糊核1 通过函数1/(i2+j2+1)产生，i、j分别表示水平、垂直方向上的数值；模糊核2 通过文献［23］复原算法在高能闪光X 射线静态投影图像上估计得到。本文中模糊核内各元素值均通过除以元素之和进行归一化处理。根据模糊核1、模糊核2 以及均值为0 方差为3 的高斯模糊核正向计算得到的透射率图像，对采用标准核和估计核下的重建结果进行实验，其中估计核通过文献［23］算法计算得到。

多模型融合前后重建结果RE 值如图4所示，其中S 和E 分别表示标准核和估计核，F 表示使用多模型融合。可以看出，在采用标准核的融合结果中，如图中的黑色实线和虚线所示，低噪声下多模型融合的效果不如噪声较严重时明显。这主要是因为在低噪声情况下，由于使用准确的模糊核，其非线性重建结果较准确，特别在无噪声情况下重建结果接近于真实值，此时多模型融合无法有效发挥其作用。而在估计核的融合结果中，由于估计的模糊核相比于标准核存在一定误差，导致在无噪声情况下重建结果一定程度偏离真实值，此时高密度区域的非线性和线性重建结果通过加权融合可得到更准确的融合结果，且随着噪声的增加，该融合作用越明显。值得注意的是，从图中红色和黑色实线可以看出，在噪声相对较严重的情况下，估计核下的融合结果比采用标准核的融合结果更加准确，说明多模型融合机制以及非线性模型中模糊核估计的有效性。

图4 多模型融合前后的RE 值Fig.4 The RE involving multi-model fusion

3.3 与现有重建算法对比实验

本小节在FTO 图像上进行实验，分别在常、变密度的FTO 透射率图像上添加0%、0.25%、0.75%、1.25%等级的高斯噪声，与现有的基于不确定度分析的重建算法LRIS_Gamma［24］、LRIS_Jeffrey［24］、SPA［25］、S_RTO［26］以及TLE_Gibbs［27］进行比较，以验证非线性重建算法的有效性。LRIS_Gamma 和LRIS_Jeffrey 算法基于低秩理论计算目标参数闭合解，SPA 为基于参数分裂和增广的采样算法，S_RTO 非线性算法在RTO 算法的基础上近似表示雅可比矩阵的分解因子并引入低秩方法进行因子分解，有效降低算法的计算复杂度。TLE_Gibbs 为基于两级不确定度约束的高效MCMC 线性采样算法。Proposed（T_F）算法为本文的非线性重建算法，其中T_F 表示采用真实模糊核，且引入多模型融合处理；I_nF 表示非线性模型下的线性解，即模糊矩阵B=I；Proposed 表示本文采用估计模糊核的非线性重建算法。

为进行定量分析，表1 与表2 给出了无加权中值滤波后处理情况下常、变密度FTO 透射率图像重建结果的PSNR 和SSIM 值。可以看出，由于模型的准确构建非线性重建算法的性能优于线性重建算法。除Proposed（T_F）算法使用真实模糊核外，本文算法（采用估计核）的非线性重建结果在所有算法中具有最佳的指标值，在噪声干扰较严重情况下，SSIM 值甚至优于Proposed（T_F）算法。此外，随着噪声的增加，在1.25%噪声水平下，本文算法整体重建性能超越Proposed（T_F）算法。

表1 常密度FTO 重建结果的PSNR 和SSIM 值Table 1 The PSNR and SSIM of reconstructed results of constant density FTO images

表2 变密度FTO 重建结果的PSNR 和SSIM 值Table 2 The PSNR and SSIM of reconstructed results of variable density FTO images

图5、6 分别对比了1.25%噪声水平下变、常密度FTO 透射率图像的重建结果。从图中可以明显地看出，SPA、LRIS_Gamma 以及LRIS_Jeffrey 算法受模型不准确的影响重建结果中仍存在较严重的噪声。和其他线性算法相比，TLE_Gibbs 重建结果在常密度区域相对平滑，但在中垂线区域连贯性较差。S_RTO 算法的重建结果中噪声较少，但由于该算法未对受不合理采样的超参数影响而未收敛的目标解进行有效约束，重建均值中仍存在边缘模糊的问题。Proposed（I_nF）算法重建结果的中垂线部分误差较大，且与线性结果类似，均存在边缘模糊问题。Proposed（T_F）以及本文算法（采用估计的模糊核）的重建结果与真实值最为接近，能较好地抑制噪声，在高密度区域能够得到较高精度的重建结果，且本文算法重建结果在图像中垂线附近优于Proposed（T_F）算法。

图5 1.25%噪声等级下变密度FTO 透射率图像重建结果Fig.5 Reconstructed results of FTO transmission image with variable density（1.25% noise level）

图6 1.25%噪声等级下常密度FTO 透射率图像重建结果Fig.6 Reconstructed results of FTO transmission image with constant density（1.25% noise level）

3.4 非密高能闪光X 射线图像重建

图7（a）为4 MeV 能级下的非密高能闪光X 射线静态图像，图像分辨率为2 048×2 048，每像素对应的目标尺寸为0.096 mm。蓝色虚线框内的实验目标为倒置的锥台，材质为锡，锥台的标准密度为7.3 g/cm3。红色实线框中3# ～4#为标记块，材料为锡，采用LM 算法拟合透射率-面密度曲线［28］。受算法采样效率以及计算平台内存的限制，线性重建实验在降采样后分辨率为350×350 的图像上开展，非线性重建实验由于需要消耗更多的内存空间在分辨率为200×200 的图像上开展。重建结果如图8所示，可以看出，GPSR 算法重建结果仍存在中心竖直剖线区域连贯性较差的问题，LRIS_Jeffrey 和LRIS_Gamma 算法重建结果中目标常密度区域较平滑，但在锥台等腰区域较为模糊。SPA 与TLE_Gibbs 算法重建结果相近，重建目标边缘较LRIS 算法更清晰，但在锥台下表面附近的常密度区域，其重建结果不如本文非线性算法重建结果平滑。与线性重建结果相比，非线性算法能够较明显地对图像背景噪声进行有效抑制。此外，本文非线性算法重建结果在锥台等腰区域具有较好的视觉效果，在统一的滤波算法的作用下六种算法的重建图像均比较平滑，得益于提出的多模型融合策略，本文非线性算法的重建结果中常密度区域的平滑性最好。

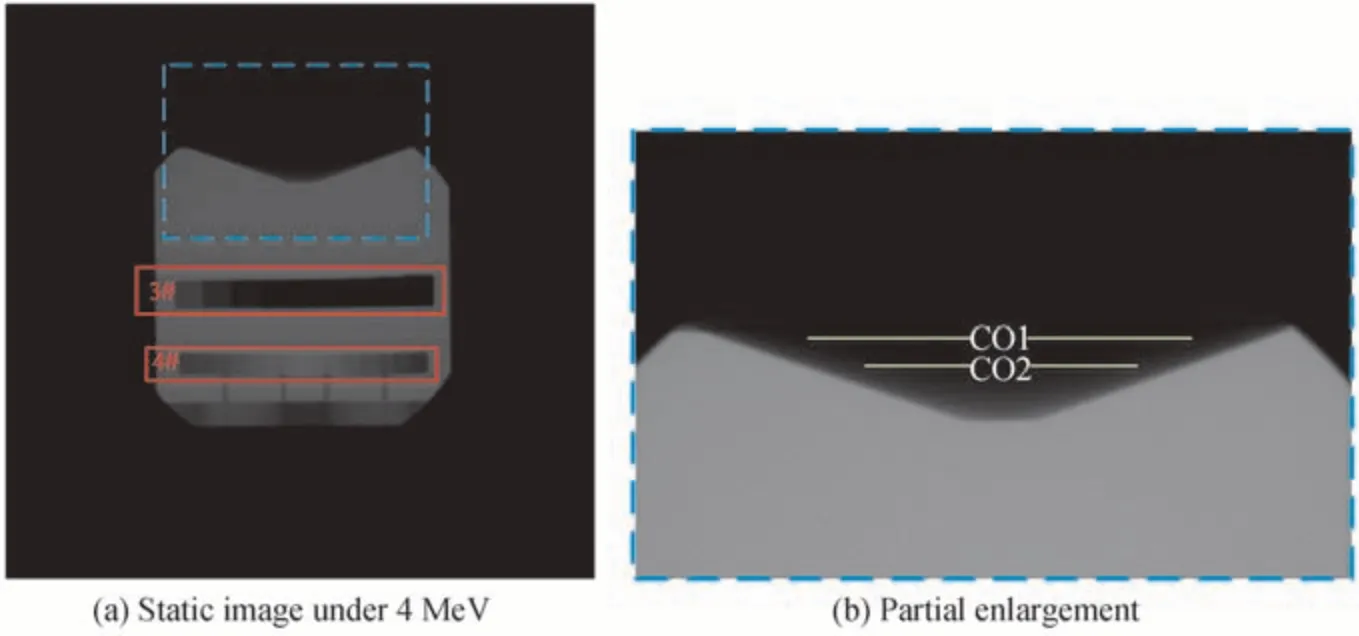
图7 4 MeV 高能闪光X 射线静态图像Fig.7 High energy flash X-ray static image under 4 MeV

图8 密度重建结果（4 MeV 静态图像）Fig.8 Results of density reconstruction（4 MeV static image）

为了更加直观地对比不同算法的重建结果，图9 给出了各算法在CO2、CO1 处的密度剖线对比，其中黑色实线表示标准密度值。可以看出，本文非线性重建结果的剖线在所有算法中最为平稳且更接近标准值，即使在锥台中垂线区域，非线性算法的重建结果相比于线性结果也更为平稳、准确，在重建精度上具有明显优势。表3 列出了上述六种重建算法在不同剖线段的密度重建均值及相对误差。对于锥台区域，LRIS_Jeffrey 和LRIS_Gamma 算法重建精度在CO1 剖线段则高于GPSR 和SPA 算法，在CO2 剖线段与SPA 算法接近，说明低秩近似理论更适用于具有单一结构目标的重建。本文非线性重建算法的重建精度优于线性重建算法，在所有算法中排名第一，其主要原因在于该非线性重建算法进行了多物理模型的融合，在方差最小化准则下合理分配加权系数，兼顾线性和非线性解的优点，有效提高了非线性模型样本估计的准确性。

表3 各算法密度重建均值（g/cm3）及相对误差（%）Table 3 Average value（g/cm3）and relative error（%）of density reconstruction of each algorithm

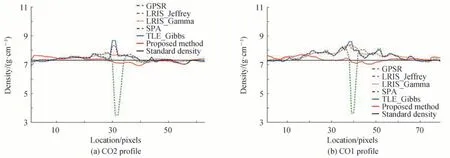
图9 各算法重建的密度剖线对比Fig.9 Comparison of reconstructed density profiles of each algorithm

4 结论

本文结合估计的模糊核，提出了一种随机扰动优化和多模型融合的高能闪光X 射线图像非线性重建算法。该算法从贝叶斯理论的角度考虑高能闪光X 射线图像非线性重建问题，构建分层贝叶斯重建模型。基于随机扰动的RTO 算法，结合雅可比矩阵投影约束求解该非线性优化模型，并在M-H 框架中通过对样本概率密度函数的近似有效提高了样本接受判别的计算效率。最后，在样本统计量方差最小化准则下提出了一种多模型融合方案，逐像素地对非线性和线性重建结果分配相应的加权系数，得到融合后更准确的重建结果。与现有重建算法的对比实验证明了本文非线性重建算法的有效性。

由于目标参数维度较高，重建速度还需进一步提升。如何引入尺度化机制减小所需求解的目标参数的维度从而提高非线性重建的计算效率，并在替代模型较多情况下结合不确定度对各模型权重进行约束从而获得更准确的重建结果，仍需要进一步深入研究。