基于改进A*和人工势场算法的无轨胶轮车井下无人驾驶路径规划

2022-04-01鲍久圣张牧野葛世荣袁晓明王茂森

煤炭学报 2022年3期

鲍久圣，张牧野，葛世荣，刘琴，袁晓明，王茂森，阴妍，赵亮

(1.中国矿业大学机电工程学院，江苏徐州 221116；2.中国矿业大学(北京) 机电与信息工程学院北京 100083；3.中国煤炭科工集团太原研究院有限公司，山西太原 030006)

近年来，我国开始加快推进煤矿智能化建设，无轨胶轮车作为煤矿井下重要辅助运输装备，无人驾驶是其智能化发展的必然方向。无人驾驶技术主要包括感知、定位、规划、决策等几大部分，其中路径规划是无人驾驶执行过程中尤为重要的环节。由于井下运输任务存在不确定性，巷道工况也存在未知性，因此需针对无轨胶轮车井下行驶巷道运输路线，研究科学高效的路径规划算法从而实现最优路径行驶。同时由于井下无轨胶轮车的工作环境中存在岔路口造成的盲区较多、未知突发情况较多、井下照度低、场景单一导致的定位依据少、网络改造力度不够等情况，且其研发需要考虑矿区的行业标准和安全生产指标，故其在工作中需要着重考虑路径选择和避障工作的先进性和准确性。

路径规划包括2种：一种是依据已知环境的前提下寻找从初始位置至目标位置的可通行路径问题，即全局路径规划；另一种是依据部分或全部环境信息未知情况下的障碍物规避问题，即局部路径规划。目前，无人驾驶车辆的路径规划算法已有较多研究，全局路径规划主要有A*算法、蚁群算法、遗传算法等；局部路径规划中常用的有人工势场算法、神经网络算法、粒子群算法等。不同算法均存在各自的优缺点，其中A*算法相比于其他全局路径规划算法，自身的可移植性和可塑性较强，简单易实现，计算量小，复杂度低，只要存在起始点至目标点的路径就一定能找到最优路径，在全局路径规划中应用较为广泛，但是当障碍物密集、环境复杂时，A*算法效率较低，启发性信息具有很大的主观性选择难度加大，难以搜索出最优路径。而且，在传统A*算法中，没有对路径进行平滑处理，因此规划路径的转折比较剧烈，不利于移动机器人的路径跟踪。人工势场算法是一种最为常见的局部路径规划方法，利用该方法可以实时避开障碍物且能规划出平滑的轨迹，实时性强、便于底层实时控制、规划路径较为平滑，有利于无人车实际控制。但是，人工势场法仅仅利用局部信息，可能会使得机器人陷入局部极值点或者不能到达目标位置。当不同的势场综合作用的效果大小相同、方向相反时，还会出现往复运动的可能。

针对传统A*算法和人工势场法的不足，已有不少学者进行了改进研究。例如，汪首坤等提出了A*算法的变步长分段搜索法，解决了应用传统A*算法搜索数据量大和搜索死循环等问题，提高了运算效率和避障效果；文献[10]提出跳点搜索策略，减少了遍历过程中所需访问的节点数，运行速度很快，但路径中仍存在转折点；文献[11]提出将混沌理论的搜索算法引入人工势场法的势场函数中，改变障碍物的斥力系数和目标点的引力系数，该方法解决了传统人工势场法的缺陷，如局部最优问题等；丁家如等采用预规划基于威胁分布的全局性信息的方法，弥补人工势场法易陷入局部最小而无法找到可行路径的不足。在井下机器人路径规划方面，针对传统算法的不足，程新景基于A*算法和DWA算法对煤矿救援机器人进行了全局路径与局部路径的研究；刘停在机器视觉的基础上，基于粒子群和蚁群算法的改进融合对井下救援探测机器人的路径规划问题进行了研究。但是，目前对于井下无轨胶轮车路径规划算法的研究尚鲜有涉及。

煤矿井下巷道空间狭小，在长、宽、高三维空间方向上均受到限制，多数情况下无轨胶轮车井下行驶路径相对固定，但在行驶途中经常会遭遇往来行人、车辆等动态障碍物，因此可以考虑选择简单易实现且计算量小的A*算法用于无轨胶轮车的全局路径规划，选择计算量小、适合底层实时控制、动态避障效果好的的人工势场算法用于无人驾驶无轨胶轮车局部路径规划。笔者将在传统A*算法和人工势场算法的基础上，针对无轨胶轮车井下无人驾驶的路径规划需求对其进行算法改进研究。

1 全局路径规划A*算法改进

笔者基于对常用路径规划算法的对比分析，选择简单易实现的A*算法用于无人驾驶无轨胶轮车全局路径规划的基本算法，并针对井下行驶工况对其进行改进处理。

1.1 传统A*算法井下应用局限性分析

A*算法建立在Dijkstra算法和最佳优先搜索(BFS)基础之上，是一种启发式搜索算法。其中，Dijkstra算法由起始点对图中全部可行点进行遍历，搜索一条最优路径，BFS则是从起点向外搜索至目标点。A*算法在BFS算法的基础上增加目标导引，既保证图搜索概率的完备性，也提高路径规划效率。

..传统A*算法原理

A*算法是经典的启发式搜索算法，它是在经典单源路径算法Dijkstra算法的基础上改进而来。其最显著的特点就是，通过在搜索过程中给定启发函数来减少搜索节点，从而提高路径搜索效率。A*算法的估价函数()表示为

()=()+()

(1)

式中，()为起始点至目标点的预估消耗；()为起始点至当前节点的实际消耗；()为当前节点至目标点的估计消耗，也称为启发函数。

A*算法路径规划过程如下：定义初始位置和目标位置后，A*算法有方向有目的的向目标位置搜索，寻找离当前点()最小的节点，寻找到该点后，将该点作为下一个基础点，继续寻找距该基础点()值最小的点，循环上述过程直到寻得目标位置所在点。

..传统A*算法井下应用存在的问题

图1 传统A*算法规划的路径Fig.1 Path planning with traditional A* algorithm

A*算法是一种易实现的算法，但将其直接应用于无人驾驶无轨胶轮车的全局路径规划是不合适的，原因在于其优化后得到的路径冗余点较多，且该方法得到的运动路线折线多、转折次数多、转折角大，这些缺陷严重影响了路径规划的效果。这对于无轨胶轮车的控制非常不利。此外，A*算法是一种搜索式算法，搜索过程需要耗费大量时间，如图1所示，对于无轨胶轮车来说，大部分时间运行在无障碍区域，如果能够加快A*算法在无障碍物区域的搜索效率，减少在无障碍物区域的搜索量，这无疑将提升路径规划的效率。

1.2 基于指数加权和样条插值的A*算法改进

针对传统A*算法存在的搜索速度慢、搜索节点多、路径不平滑的缺点，笔者从以下2个方面进行A*算法改进。

..估价函数优化

A*算法在搜索路径时，启发函数值决定了其搜索效率，由于当前节点到目标点所消耗的()总是小于当前点至目标点的实际消耗，所以在搜索过程中需要搜索过多的节点。如果当前节点到目标点的估计消耗等于实际消耗，那只需1次搜索即可到达目标点。如果能够提升估计消耗()的权重，搜索的节点数将会减少，算法效率将得到提升，基于此方法，赵真明等对启发函数进行了加权：

()=()+()

(2)

其中，为权重系数。经过加权改进后，算法的搜索效率得到了提升。但在实际搜索过程中，随着当前节点逐渐接近目标点，预估消耗()会逐渐接近真实消耗，此时权值应逐渐接近于1，使用固定的权重系数显然无法在接近目标点使预估消耗接近真实消耗。因此，笔者在文献[20]的方法基础上进行改进，使用预估消耗的指数函数作为启发函数的加权系数，优化后的估价函数为

()=()+e()()

(3)

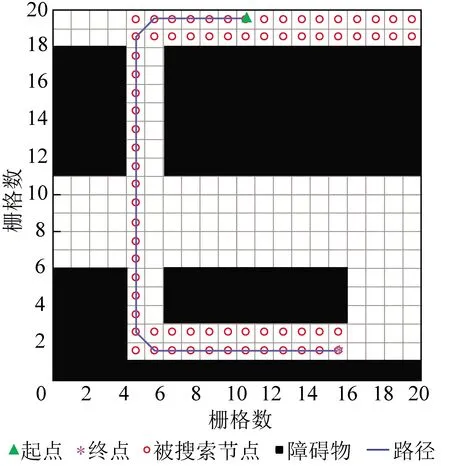
图2 加权A*算法规划的路径Fig.2 Path planning with weighted A* algorithm

在式(3)中，随着当前节点逐渐接近目标点，预估消耗()逐渐趋近于0，加权系数逐渐趋近于1。图2为加权后的A*算法搜索节点数，相比图1规划的结果大大减少。传统A*算法搜索节点数为123个，搜索时间为0.875 4 s，改进后算法搜索节点数为66个，搜索时间为0.182 6 s，计算可得加权后的A*算法搜索时间仅为传统A*算法的20%左右。

..路径平滑处理

启发函数加权改进后的A*路径算法能够快速搜索出1条从起点至目标点的路径，不过路径上存在拐点的情况依然没有解决，无轨胶轮车跟踪这样的路径时会出现较大且不平稳的转向，不利于无轨胶轮车的实际控制，需对这样的路径进行平滑处理。常用的路径平滑方式有高阶贝塞尔曲线、圆弧处理和三次样条插值法等。对于三次样条曲线，只需给定路径坐标信息和边界条件即可拟合出1条光滑的曲线，笔者选择三次样条插值对改进后A*算法规划的路径进行平滑处理。

三次样条插值定义如下：如果存在这样的分段函数()，在+1个离散点构成的个不同的任一区间[，+1](=0，1，2，…，-1，递增)中，()=()都是三次多项式，且在任意点处都满足()=(=0，1，2，…，)，那么可将这样的函数称作三次样条插值函数。()具有二阶导数，且其二阶导数在区间[，]内是连续的，也可以理解为()曲线是一条光滑曲线，因此使用该函数拟合出的路径也必然是光滑的。

对于使用指数函数加权后A*算法规划出的路径，不需要对全部路径点进行三次样条插值，只需对转折处进行插值拟合即可，使用三次样条差值平滑处理前后的路径对比如图3所示。图3(a)为使用指数函数加权后A*算法规划出的路径，转折点较多，路径不平滑，图3(b)为使用三次样条插值法处理后的路径，虽然还有一些微小的转折，但路线基本平滑。

1.3 基于改进A*算法的全局规划仿真

无轨胶轮车在井下行驶时经常通过联络巷变换到其他巷道，如图4所示。本节使用指数函数加权后A*算法模拟无障碍物情况下无轨胶轮车从当前巷道(图4中巷道1)通过联络巷进入另一条巷道(图4中巷道2)时的路径规划，对规划出的路径使用三次样条插值法进行平滑处理，仿真试验相关参数设置见表1。

指数加权后A*算法规划的路径如图5(a)所示，使用三次样条插值处理后的路径如图5(b)所示。

由图5可看出，路径规划过程中搜索节点数较少，都在其规划的路径上，具体搜索节点数为37个，所用时间为0.075 74 s。同时，也应该看到使用指数加权后的A*算法不能消除路径上的拐点，因此需要使用三次样条插值法对指数函数加权后A*算法规

图3 平滑处理前后路径对比Fig.3 Path comparison before and after smoothing

图4 巷道变换示意Fig.4 Schematic diagram of roadway change

表1 A*算法路径规划仿真参数设置

图5 改进后A*算法规划的路径Fig.5 Path planned by the improved A* algorithm

划的路径进行平滑处理，平滑处理后的路径无明显转折点，且处理后的路径与处理前差距在一个栅格内，可以保证平滑处理的安全性，比处理前的路径更符合无轨胶轮车运动学约束。

2 局部路径规划人工势场算法改进

选择实时性强的人工势场算法用于无轨胶轮车井下无人驾驶局部路径规划的基本算法，通过改进处理使其满足需求。

2.1 人工势场算法井下应用局限性分析

人工势场算法是一种模拟物理力场的算法，它的基本思想是将机器人在周围环境中的运动，设计成一种抽象的人造引力场中的运动，目标点对移动机器人产生“引力”，障碍物对移动机器人产生“斥力”，最后通过求合力来控制移动机器人的运动。

..传统人工势场算法原理

无人车在行驶途中最大的人工势场引力源自目标点，当势力场为0时，2者之间距离为0，表示车辆已到达目标点。无人车只有在障碍物势场范围内才会受到斥力势场的影响，在障碍物势场范围内，无人车受到的势场斥力与无人车和障碍物之间的距离成反比。势力场函数用于描述运行过程中目标点和障碍物对无人车产生的影响，需要考虑无人车向目标点移动的效率问题来构建专门的函数衡量势场的大小。

在构建的虚拟人工势场中，无人车受到的力是障碍物的斥力和目标点的引力的合力，该合力为矢量，合力的方向决定了无人车的行驶方向。障碍物的数量可能不止一个，因此无人车可能会受到多个斥力作用，在使用人工势场算法做路径规划时，要将无人车受到的所有斥力和引力按矢量运算原则相加，在合力的作用下向目标点靠近，如图6所示。

图6 人工势场中车辆受力示意Fig.6 Schematic diagram of vehicle force in artificial potential field

..传统人工势场算法井下应用存在的问题

人工势场算法起初主要应用于机器人局部路径规划，随着无人驾驶技术的发展才逐渐应用于地面车辆的路径规划中。机器人在使用人工势场法进行路径规划时很少考虑道路的约束，但是无人车的运动状态是时变的，障碍物数量、形状和位置也具有不可预知性，导致无人车在构建的虚拟势场中会出现局部最优解和目标不可达问题。当无人车在某个引力与斥力大小相等，方向相反的位置时，无人车受力为0，陷入局部最优解。当目标点与障碍物之间的距离较近时，斥力非常大，引力相对较小，导致无人车出现目标不可达。

在地面无人驾驶车辆的路径规划过程中，经典的做法是建立车道线势场，此前也有研究人员将人工势场算法用于煤矿机器人的路径规划，但是没有考虑巷道的约束，故难以直接用于无轨胶轮车在井下巷道内的无人驾驶。

2.2 基于巷道斥力势场的人工势场算法改进

针对传统人工势场算法存在的局部最优解和目标不可达问题，笔者将从2个方面进行改进，并建立移动障碍物相对速度斥力势场。

..斥力势场修正因子

为了解决传统人工势场算法目标不可达问题，笔者针对巷道壁和障碍物的斥力分别进行修正。根据《煤矿安全规程》相关规定，无轨胶轮车与巷道壁之间的最小距离应≥0.3 m，人行侧应保留至少0.8 m，因此将距离巷道壁0.8 m以内的区域设置为高危区域，其余位置为低危区域。根据不同危险程度，建立分段函数来表示巷道空间约束势场，在离巷道壁距离小于0.8 m的区域使用变化较快的指数函数建立巷道空间约束势场，在离巷道壁距离大于0.8 m的区域低危险区域使用三角函数来建立巷道空间约束势场，建立巷道空间约束势场函数为

(4)

式中，为高危区域斥力势场强度系数；为低危区域斥力势场强度系数；为巷道宽度；为无轨胶轮车几何中心距巷道壁距离；，，为常量系数，由巷道宽度决定。

取=10，=20,=8，=1，=5/22，=9/11，根据式(4)建立的巷道空间约束势场图，如图7所示。

图7 巷道空间约束势场Fig.7 Roadway space constrained potential field

由式(4)和图7可知，在靠近巷道壁0.8 m内(高危区域)斥力势场较大，且变化趋势很快，靠近巷道中间位置的区域斥力势场较小，变化趋势也相对缓和，在巷道正中间巷道空间约束势场强度为0。

引入斥力势场修正因子对障碍物斥力势场进行修正，修正后的斥力势场函数为

(5)

式中，为斥力势场强度(正比例增益因子)；为障碍物所在位置(,)；为目标点所在位置(，)；为斥力势场的最大作用距离，为常数；-为无人车与障碍物之间的距离；-为无人车与目标点之间的距离；为修正因子系数，>0。

由式(5)可知，无人车到达目标地点时，=，无人车不受斥力势场影响，因此引入修正因子可使无人车到达终点时处于0势能点。

与原斥力势场相比，引入修正因子后的斥力势场随着无人车和目标点之间距离的减小呈衰减趋势，取值不同，衰减趋势也不同。将起点设置为(0,0)目标点坐标设置为(1,1)，可得势场衰减趋势如图8所示，越大，斥力势场衰减越快，同时，如果取值过大，斥力势场衰减过于迅速，可能导致无人车避障失败，因此的取值应当兼顾衰减趋势和避障效果。

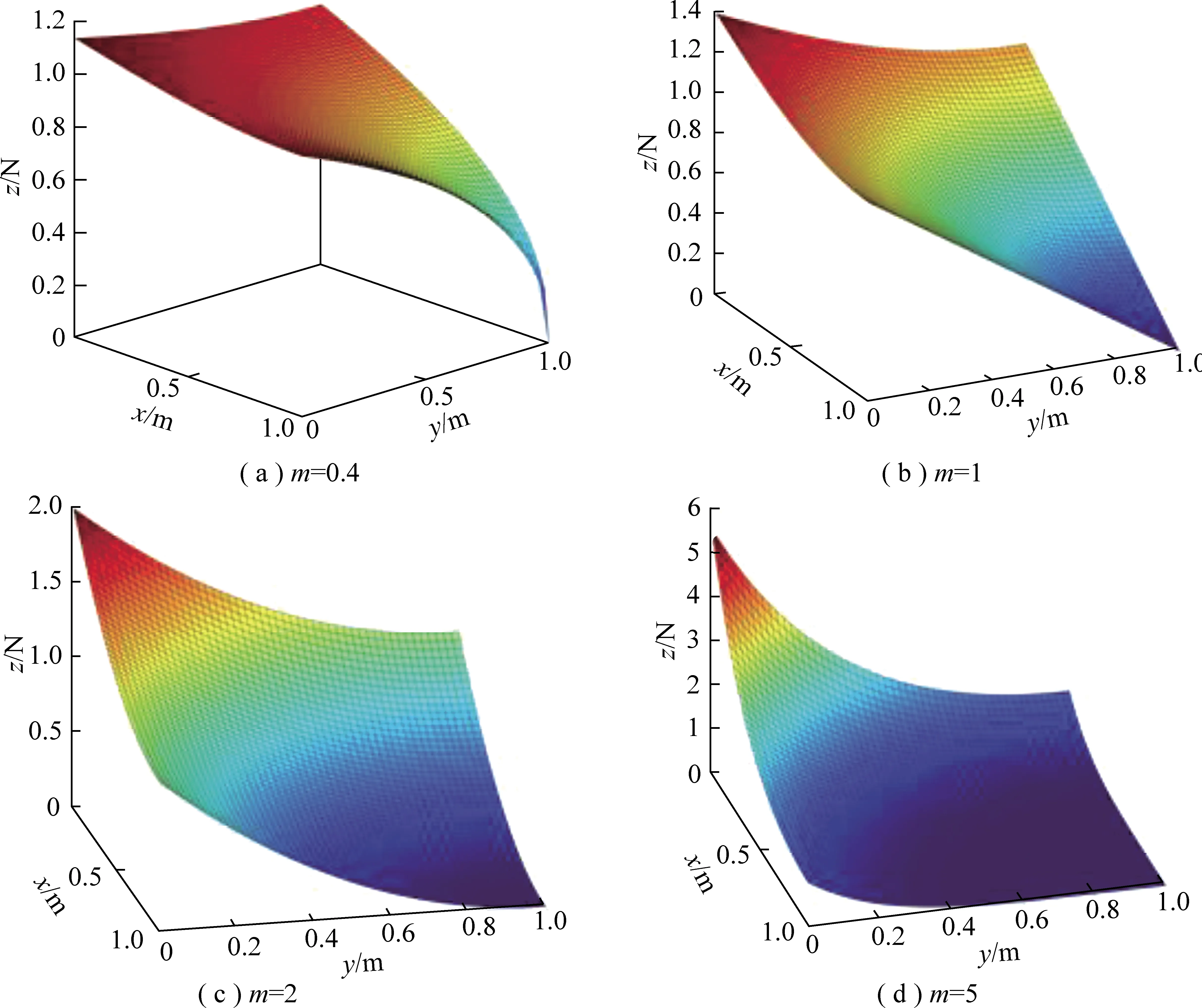
图8 不同修正因子下的斥力势场衰减趋势Fig.8 Attenuation trend of repulsion potential field under different correction factors

当≠时，修正后的障碍物斥力函数为

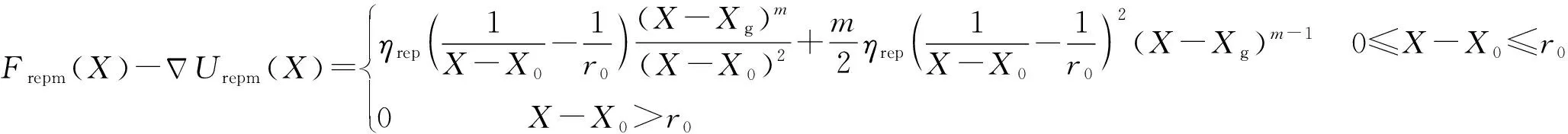
(6)

(7)

(8)

式中，与为的2个分力，这2个分力指向不同方向，的方向为障碍物到无人车，的方向与相反。

修正因子系数不但影响斥力势场衰减趋势，还影响无人车受力情况，具体情况为：

(1) 0<<1时

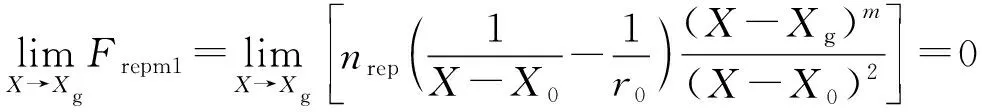
(9)

(10)

无人车接近目标位置时，→0，→∞，无人车在和的合力作用下驶向目标位置。

(2)=1时

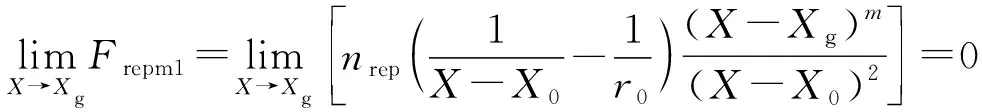
(11)

(12)

无人车接近目标位置时，趋近于0，趋近于一个常量，无人车在和的合力作用下驶向目标位置。

(3)>1时

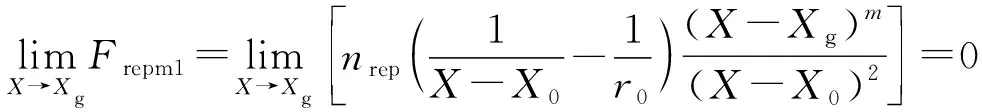
(13)

(14)

无人车接近目标位置时，趋近于0，也趋近于0，无人车在的作用下驶向目标位置。

取=1，斥力系数设置为100，引力系数设置为10，起点设置为(0,0)，终点设置为(80,80)，改进后的人工势场算法仿真实例如图9所示。由图9可知，改进后的人工势场算法可解决目标不可达问题。

图9 解决目标不可达仿真实例Fig.9 Simulation example of solving target unreachable

..出逃力引入

对斥力函数进行修正后，无人车的目标不可达问题得到解决，但仍无法解决局部极小值问题。为此，笔者引入了出逃力。在无人车陷入局部极小点后，判断是否到达目标点，如若没有，由出逃力帮助无人车逃出局部极小值点，出逃力的大小随机赋值，但其方向需与引力方向或斥力方向垂直。然而，巷道比较特殊，如若在单车道巷道中陷入局部极小值点，代表前方有障碍物不可通行，如图10所示，此种情况下不用引入出逃力，应立即停车,引入出逃力后程序运行流程如图11所示。

图10 单车道巷道内陷入局部极小值示意Fig.10 Schematic diagram of falling into local minimum in single lane roadway

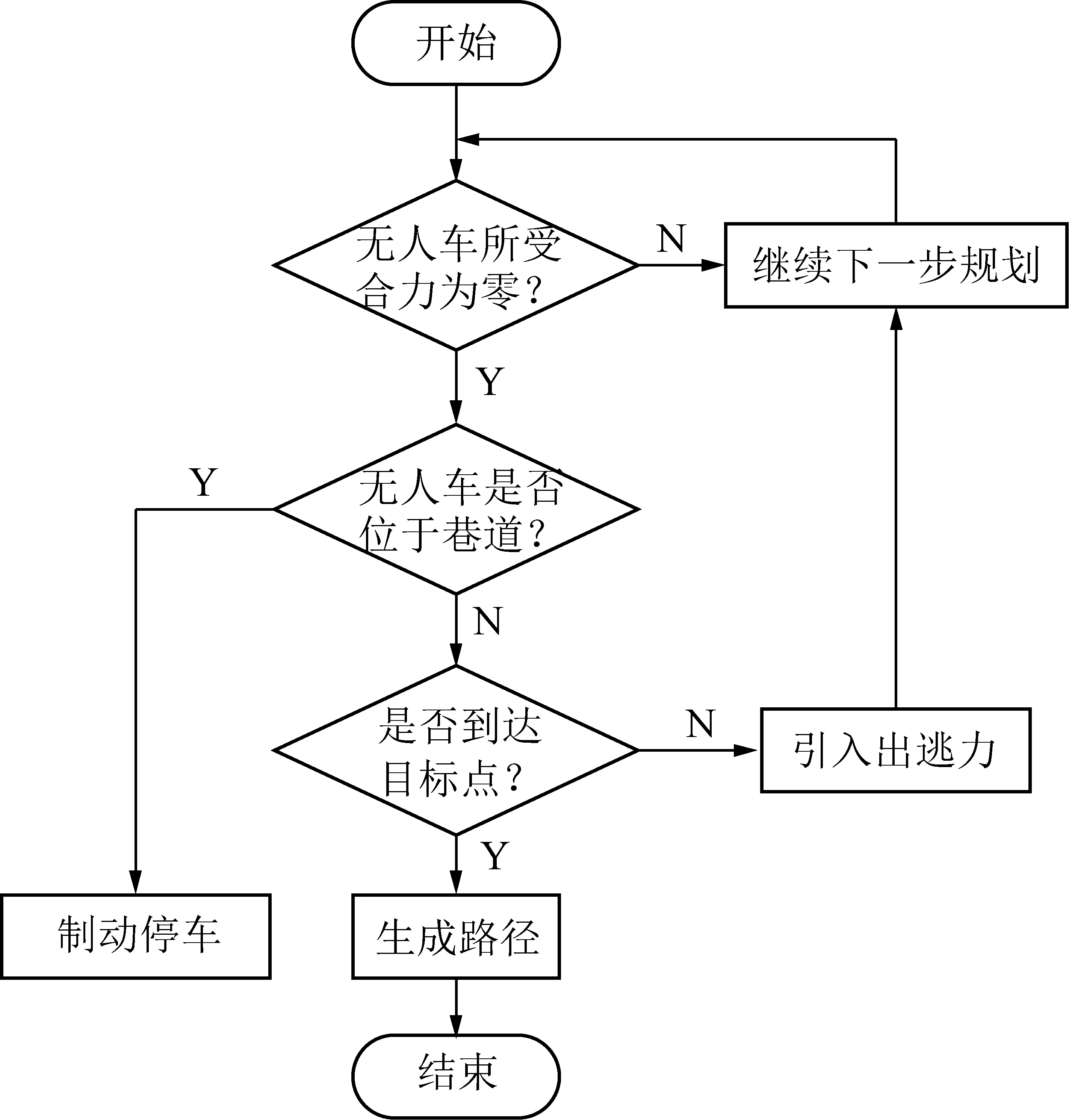
图11 引入出逃力后路径规划流程Fig.11 Path planning process after introducing escape force

斥力系数设置为100，引力系数设置为10，起点设置为(0,0)，终点设置为(90,90)，出逃力以随机数的方式给出，仿真实例如图12所示，在陷入局部极小值后，出逃力将无人车带离局部极小值点，继续向前行驶，到达目标点。

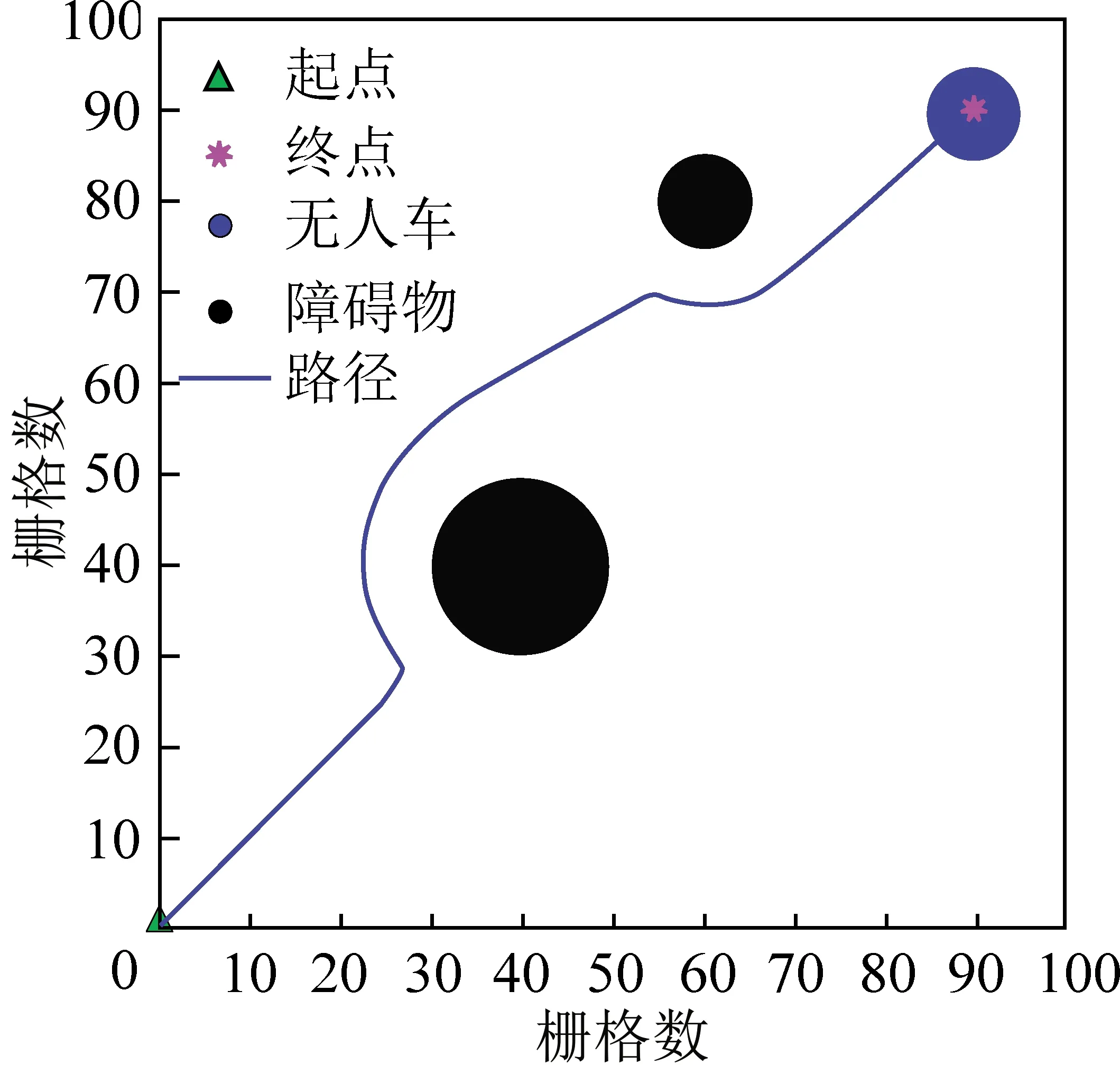
图12 解决局部极小值仿真实例Fig.12 Solve local minimum simulation example

..相对速度势场建立

无轨胶轮车有时也运行在其他环境，这时障碍物为动态障碍物。传统人工势场法在引入斥力衰减系数和出逃力后，可解决目标不可达和局部最优。为了提升人工势场算法在动态避障中的可靠性，笔者进一步引入无人车与障碍物的相对速度势场函数：

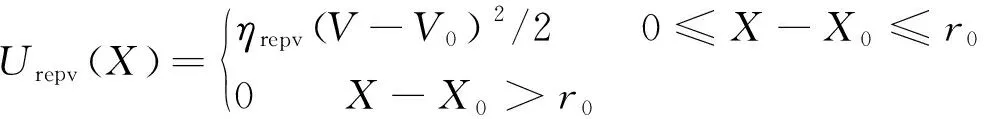
(15)

无轨胶轮车与动态障碍物相对速度势场斥力为

(16)

式中，为无轨胶轮车当前速度矢量；为动态障碍物当前速度矢量；为相对速度势场系数。

2.3 基于改进人工势场算法的局部规划仿真

无轨胶轮车在巷道内的局部路径规划场景需求主要有：单车道遇对向来车、双车道遇对向来车以及交叉巷道中2个及以上方向有来车时的会车避让，下面将对上述3种场景进行局部路径规划仿真试验。

..单车道会车路径规划仿真试验

单车道会车时避让过程如图13所示，假定A车为运人车辆，B车为运料车辆，根据井下行车规则：A车应减速行驶，B车应进入躲避硐室，待A车通过会车区域后，B车再驶出躲避硐室继续向前行驶。仿真结果如图14所示，分析可知，在单车道会车场景下当前车辆B车能规划出合理安全的行车路径。

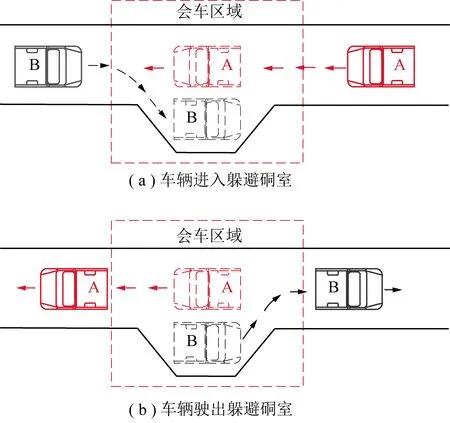
图13 单车道巷道会车过程示意Fig.13 Schematic diagram of the meeting process of single-lane roadway

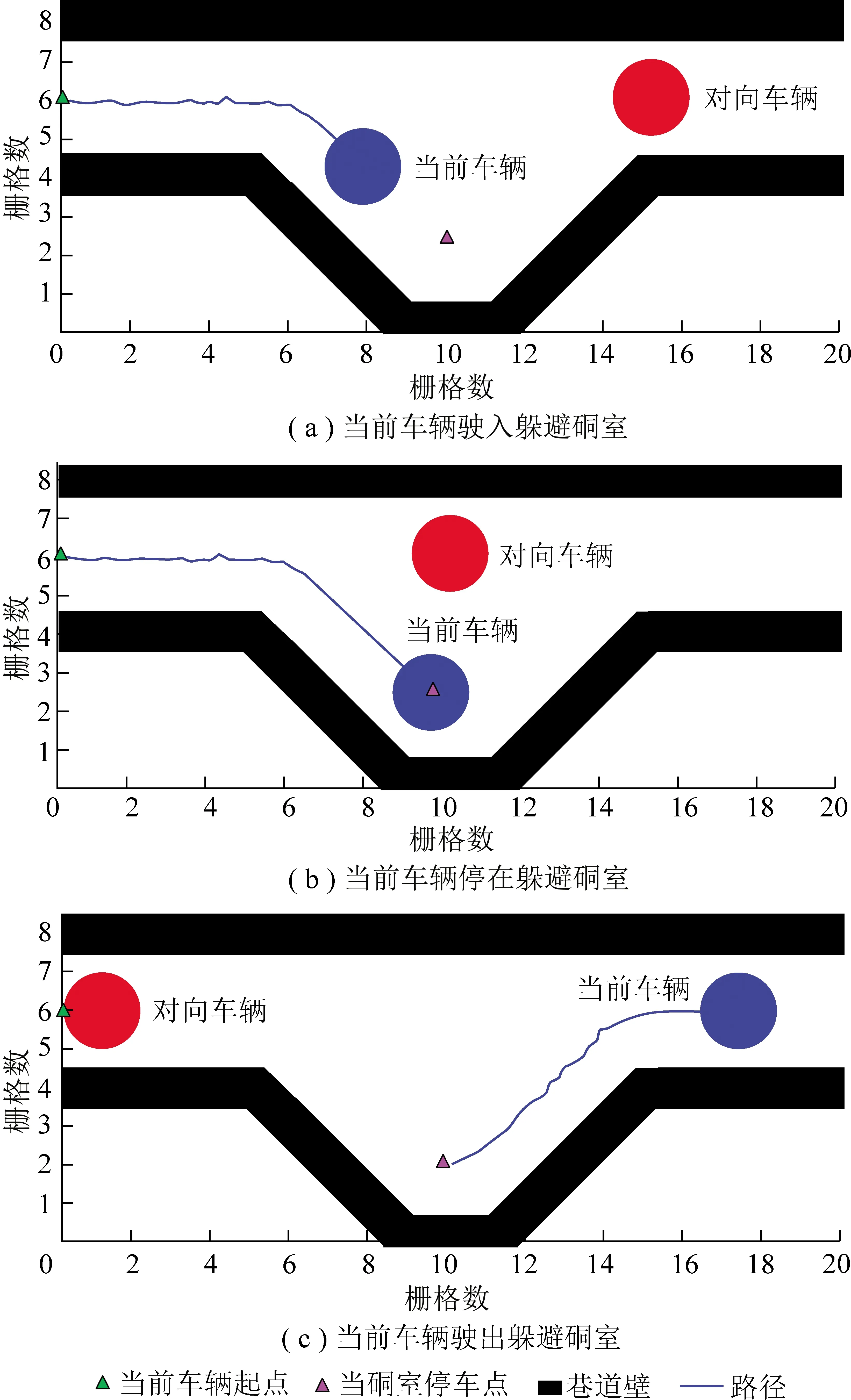
图14 单车道巷道会车路径规划仿真Fig.14 Single-lane roadway meeting path planning simulation

..双车道巷道会车路径规划仿真

双车道会车时避让过程如图15所示，假定2辆车在水平巷运行，A车为运人车辆，B车为运料车辆，根据井下行车规则：A车应减速行驶通过会车区域，B车应靠边停车，待A车通过会车区域后B车再继续向前行驶。仿真结果如图16所示，分析可知，在双车道巷道会车场景下当前车辆A车能规划出合理安全的行车路径。

图15 双车道巷道会车过程示意Fig.15 Schematic diagram of the two-lane roadway meeting process

图16 双车道巷道会车路径规划仿真Fig.16 Two-lane roadway meeting path planning simulation

..交叉巷道会车仿真

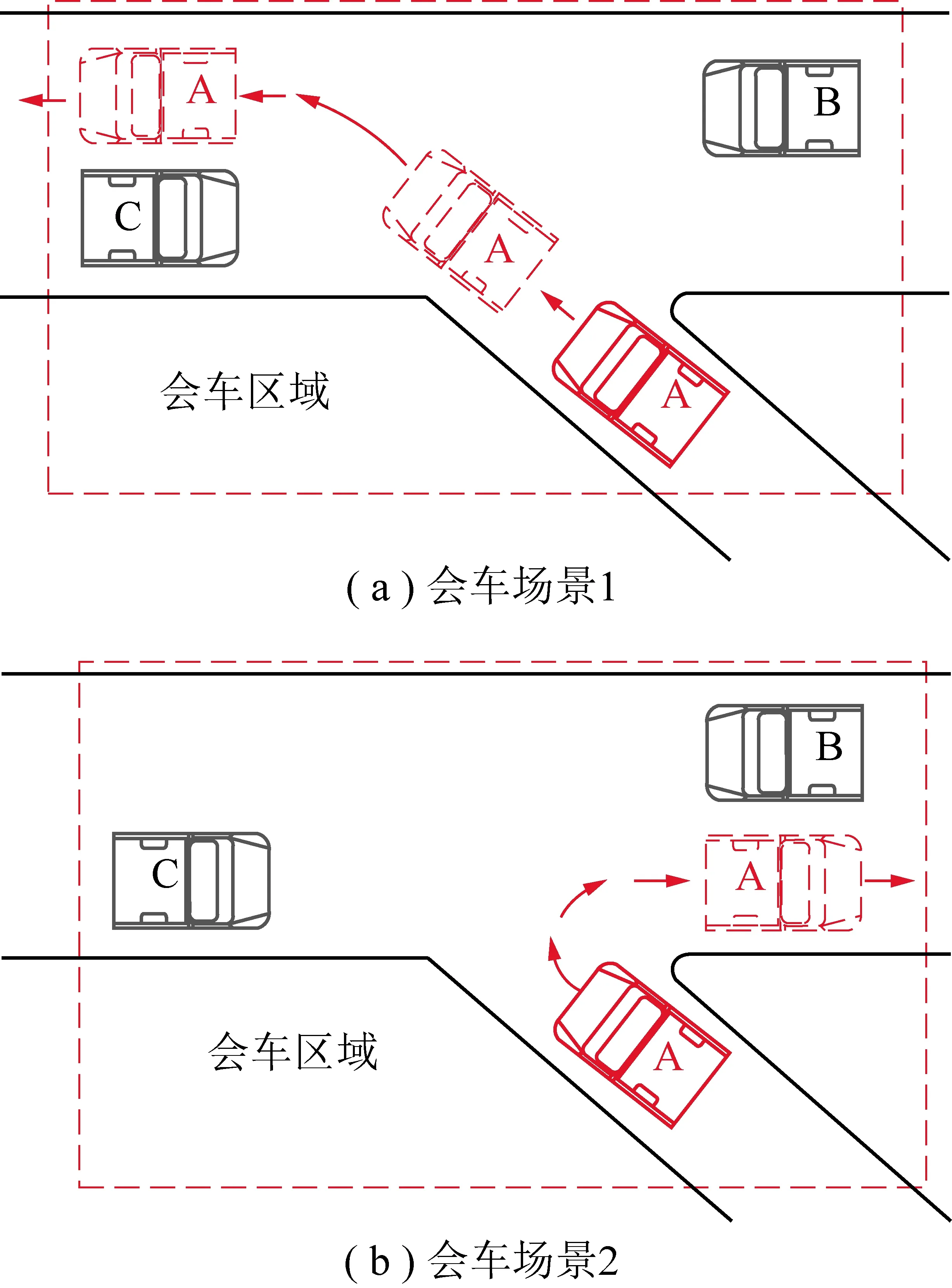
图17 交叉巷道会车过程示意Fig.17 Schematic diagram of the crossing roadway meeting process

交叉巷道会车流程复杂，当前《煤矿安全规程》和各大煤矿都没有针对交叉巷道制定统一的会车规则，笔者参考单、双车道巷道会车策略和交叉巷道特征，规定交叉巷道发生会车时，只允许一辆车通行，制定如下会车策略：首先根据岔道车辆先行原则进行会车，即只要岔道中有来车，则其他方向车辆进入躲避硐室(单车道巷道)或靠边停车(双车道巷道)，等待岔道车辆先行通过会车区域，待岔道车辆通过会车区域后，如只剩一辆车即按原规划路径继续行驶即可；若岔道车辆通过会车区域后还剩2辆无轨胶轮车，则判断两车后续路径是否相同，若剩余两车后续路径相同，意味着两车后续都将进入岔道，此时遵循就近原则进行会车，即离岔道口近的车辆先行；若路径不相同但其中一辆车后续进入岔道，则根据“岔道先行”原则进行会车，待进入岔道的车辆驶离会车区域后，另一辆车才按原路径继续行驶；若后续两车相向行驶，则表示剩余两车均不进入岔道，此时根据直巷类型分别根据单车道巷道会车策略或双车道巷道会车策略进行会车。假设为3个巷道均有来车，如图17所示，当前无轨胶轮车为A车，将另外两辆车视为静态障碍物，仿真分析A车的路径规划问题。A车路径规划问题又可分为2种场景，场景1为出叉巷后左转，如图18(a) 所示，场景2为出叉巷后右转，如图18(b)所示。交叉巷道路径规划仿真结果如图18所示，分析可知，当前车辆A在出交叉巷后，无论是左转还是右转，都能在有车辆的情况下规划出安全可通行的路径。

图18 交叉巷道会车路径规划仿真Fig.18 Path planning simulation of crossing lanes

3 模拟巷道内无人驾驶路径规划试验

根据《煤矿安全规程》和国家安标中心相关政策，若要在井下开展无轨胶轮车无人驾驶试验，需要对无人驾驶系统所有电气设备进行防爆处理并取得国家安标证书，试验成本高且周期很长。因此，笔者采取模拟试验的方法对前文建立的改进算法进行验证，按8∶1缩比搭建交叉巷道模型用做试验场地，在搭建好的交叉巷道模型中使用基于ROS的微型无人车开展路径规划试验。

3.1 试验场景搭建

煤矿井下交叉巷道处多为单车道巷道与双车道巷道相交叉，因此建立一个交叉巷道模型即可模拟交叉巷道会车和双车道巷道会车等多种行车场景。考虑实验室空间布置和试验成本问题，按大约8∶1的比例缩放搭建交叉巷道模型。双车道巷道长度设置为4 m，宽度设置为0.6 m，单车道巷道长度设置为2 m，宽度设置为0.4 m，巷道高度设置为0.6 m，交叉巷道模型设计如图19所示。

图19 巷道模型设计Fig.19 Roadway model design

巷道模型搭建完毕后，使用激光雷达扫描巷道模型，基于SLAM构建巷道模型地图，这是微型无人车进行路径规划的前提，基于SLAM构建的巷道模型地图如图20所示。

图20 巷道模型地图Fig.20 Roadway model map

图21 基于ROS的微型无人车Fig.21 ROS-based mini driverless vehicle

本文所使用的微型无人车如图21所示，微型无人车主要包括感知系统、决策系统、执行系统和通信系统等。感知系统中激光雷达将感知到的环境信息通过USB接口传送到决策系统，九轴陀螺仪感知到的加速度等信息首先发送给底层控制板，驱动板处理后通过串口发送给决策系统，主控制器处理环境、速度等信息后，根据处理结果进行下一步决策，将决策结果以指令的方式通过串口发送给底层控制板，控制板最后将执行指令发送给电机驱动器和舵机驱动器，驱动电机和舵机完成相应动作。上位机通过局域网和无人车决策系统连接，对无人车实施控制。

笔者搭建微型无人车的决策系统使用英伟达Jetson Nano B01开发板作为主控制器，Jetson Nano B01开发板体积小、功耗低、算力强大，可支持多个高精度传感器同时使用，广泛应用于图像处理、人工智能领域，其主要性能参数见表2。

3.2 路径规划模拟试验

由于局部路径规划是在全局路径规划的基础上进行的，所以首先对改进A*算法进行全局路径规划试验，而后在改进A*算法规划的路径上进行改进人工势场算法的局部路径规划试验。

表2 Jetson Nano B01开发板参数

..全局路径规划模拟试验

将路径起点设置于巷道模型双车道巷道入口处，终点设置在巷道模型单车道巷道出口处，如图22所示，分别使用传统A*算法和本文改进后A*算法进行路径规划，路径规划结果如图23所示。

图22 A*算法路径规划试验起点终点设置Fig.22 Setting of starting point and ending point of A* path planning test

图23 A*算法改进前后路径规划试验结果Fig.23 Experimental results of path planning before and after A* algorithm improvement

改进前后A*算法规划路径对比结果如图24所示，对比分析2条路径可知，在双车道直巷内轴与轴偏差较小，轴偏差控制在±0.02 m之内，最大偏差出现在模型试验车转弯时，为-0.031 2 m。该试验证明，改进前A*算法规划的路径拐点多，改进后A*算法规划的更加平滑，路径更加合理，更有利于微型无人车的跟踪。

图24 改进前后A*算法规划的路径对比Fig.24 Comparison of path planning of A* algorithm before and after improvement

..局部路径规划模拟试验

在模拟巷道地图已知的情况下，指定起点与终点，可使用A*算法规划出一条由起点至终点的全局路径，然而当规划好的全局路径被未知障碍物干涉或者遇到对向来车时，无人车将无法继续按照规划好的全局路径向前行驶，这时就需要使用人工势场算法进行局部路径规划，待避障或会车结束后再回到全局路径继续向前行驶，A*-人工势场算法联合路径规划具体流程如图25所示。

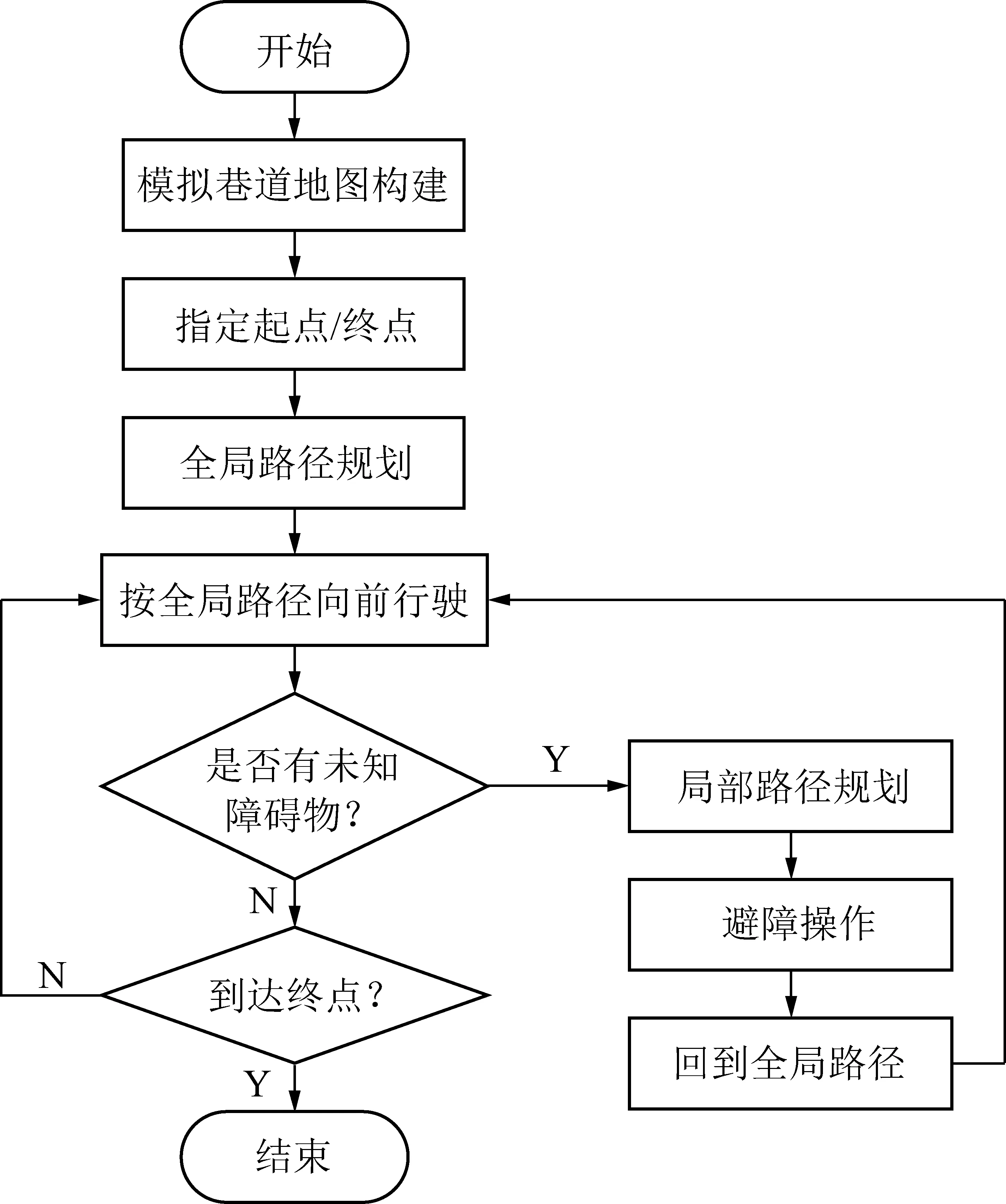
图25 A*-人工势场算法联合路径规划流程Fig.25 A*-APF combined path planning flowchart

首先，根据建立的地图以及指定的起点和终点规划全局路径，微型无人车首先按照全局路径行驶，行驶途中遇未知障碍物时使用人工势场算法进行局部路径规划，待避障结束后，再回到全局路径，重复上述过程直到微型无人车到达终点。

本组试验使用微型无人车和交叉巷道模型模拟无人驾驶无轨胶轮车巷道内会车和遇未知障碍物时的避障，起点与终点设置如图26所示，在无障碍物情况下首先使用改进A*算法规划出全局路径，规划的全局路径如图27所示。然后在长直双车道巷道中设置2个障碍物，障碍物1用于模拟对向来车，假定微型无人车为让车车辆且对向来车车体较大，需借助躲避硐室进行会车；障碍物2为未知障碍物。

图26 人工势场法试验起点与终点设置Fig.26 Setting of test starting point and end point of APF

有障碍物的情况下微型无人车规划的实际路径如图28所示，无障碍物情况下规划的全局路径与有障碍物情况下的实际路径对比如图29所示。

图27 无障碍物情况下改进A*算法规划的全局路径Fig.27 Global path planning by improved A* algorithm without obstacles

图28 微型无人车避障过程Fig.28 Mini driverless vehicle obstacle avoidance process

图29 全局路径与实际路径对比Fig.29 Comparison between global path and actual path

微型无人车首先按照规划好的全局路径行驶，行驶一段距离后遇到对向来车需进行避让，此时路径发生变化，待绕过对向来车后回到全局路径继续向前行驶，在遇到未知障碍物时为了安全避开障碍物路径发生了微小的偏移，随后回到全局路径并按全局路径行驶至终点。对比分析两条路径可知，在无障碍物的模拟巷道区域内轴与轴偏差较小，轴偏差控制在±0.01 m之间，最大偏差出现在会车时，为0.035 3 m，误差较无障碍物区域偏大，这是由于避障时车辆需要转向所致，避让障碍物时轴偏差在±0.02 m之间。试验结果证明了本文所用A*-人工势场算法规划的全局路径和局部路径是合理的。